Rep:Mod:96499348
Transition Structures
Tutorial:The Cope Rearrangement
Part A: Optimising the reactants and products in an example with 1,5-hexadiene
Using the HF/3-21G level of theory, the antiperiplanar conformation of 1,5-hexadiene was computed to have C2 symmetry and electronic energy of -231.69260235 a.u. This is expected to be lower than that of the gauche conformer that is subjected to higher steric clash between the alkyl groups (at 60 degrees dihedral angle) - this steric clash increases torsional strain and increases the energy of the gauche conformer. Still using HF/3-21G, the energy of the gauche conformer was calculated to be -231.69166702 a.u, which is higher than that of the antiperiplanar conformer, as we would expect. This structure also has a C2 point group.
The antiperiplanar conformer made corresponds to the anti1 structure in the table in Appendix 1 of the lab manual. They both have C2 point groups and exactly the same energy of -231.69260 a.u. This, according to the appendix, is also the lowest energy anti conformation. For the gauche conformer, the molecule made corresponds to gauche2 in the same table, with matching energies of -231.69167 a.u. and point group C2.
The construction of the Ci anti2 conformer of 1,5-hexadiene was then attempted. The resulting conformer's final energy was -231.69254 a.u which corresponds to the appendix. This structure was then optimised twice, separately, once with DFT 6-31G and another time at Hartree-Fock 3-21G level.
The table below shows the structure of the antiperiplanar 1,5-hexadiene antiperiplanar of Ci symmetry, optimised at HF/3-21G level (left) and optimised at DFT 6-31G level (right). The diagrams in the table show that the arrangement of the hydrogen atoms on the middle two carbons differ between the structures optimised at different levels. In terms of the geometry, the point group of the re-optimised (DFT/6-31G) structure is closer to a C2h structure than the Ci structure (which is the case for the structure optimised at HF/3-21G).
Nf710 (talk) 10:52, 19 November 2015 (UTC) you haven't shown any understanding of the methods here. Such as the differences between HF and DFT. Furthermore you have mentioned that the gauche 3 conf. is the lowest in energy due to secondary orbital interactions. However your acknowledgement of steric hinderance is acceptable. Your comparison of geometries is poor you haven't given any mention to dihedrals etc. and you haven't run a frequency calculation to check there are no imaginary frequencies.
| HF/3-21G | DFT/6-31G |
|---|---|
After a frequency calculation at DFT/6-31G, all vibrational frequencies were found to be real and positive. Results showed that:
- the sum electronic and zero-point energies computed = 234.416255 a.u. (This is the potential energy of the molecule at 0 K plus the zero-point vibrational energy.)
- the sum of electronic and thermal energies = 234.408963 a.u (This is the potential energy of the molecule at 298.15 K and 1 atm - this energy comes from the translational, rotational and vibrational energy modes under these conditions)
- the sum of electronic and thermal enthalpies = 234.408019 a.u (this contains an additional correction for RT (H = E + RT) - crucial component when investigating dissociation reactions; also includes entropy in free energy calculations)
- the sum of electronic and thermal free energies = 234.447872 a.u
Nf710 (talk) 11:18, 19 November 2015 (UTC) Good understanding of thermal energies
Part B: Optimizing the "Chair" and "Boat" Transition Structures
To understand the Cope reaction, the 'Chair' and 'Boat' transition states were investigated.
Optimising the Chair Transition State
A guess structure for the chair transition state was constructed by orienting two allyl fragments such that they resemble the chair structure, and the distance between the carbons involved in bond formation were set to 2.2 Å. To get the chair transition state, the first the force constant matrix was computed and the structure constructed was optimised to a transition state (optimising to a TS (Berny)). This was done using Hartree Fock calculation at the 3-21G level. The resulting structure had one imaginary vibration frequency of magnitude 818 cm-1, which confirms that the structure is indeed a transition state. The animation of this vibration also corresponds to the Cope rearrangement, giving confidence that this is the transition state we are looking for. This structure was then further optimised using the frozen coordinate method. After this second optimisation, the bond forming/bond breaking bond lengths are 2.0 Å, which is slightly shorter than that of the structure after the first optimisation (bond forming/bond breaking bond lengths = 2.2 Å). The transition state from both optimisations look similar but have different point groups (see table below).
| Level of Optimisation | |
|---|---|
| HTF/3-21G | Frozen Coordinate Method |
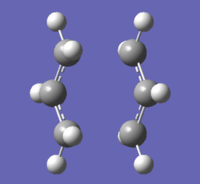 |
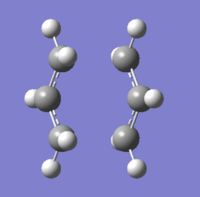 |
Optimising the Boat Transition State
To find the boat transition state, opt+freq QST2 TS optimisation at HF/3-21G level was employed. This method attemptsto find the transition state from the reactant and product.This was unsuccessful because bond rotation was not automatically considered in the computation - the figure below shows two images of the erroneous transition structures computed.
| Top View | Side View |
|---|---|
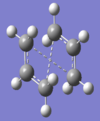 |
 |
As a result, the optimisation was repeated, but with the dihedral angle for the central 4 carbon atoms set to 0o and the two innermost angles in the molecule set to 100o for both the reactant and product. The resulting structure is shown below:
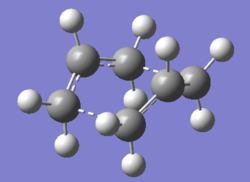
This structure has only one imaginary frequency at -840.04 cm-1, which confirms that it is indeed a transition state.
Nf710 (talk) 10:56, 19 November 2015 (UTC) your frequecies are correct but you havent shown any understanding of why they imaginary
The Intrinsic Reaction Coordinate (IRC) method is then used to find the minimum energy path from a transition state to its local minimum on a potential energy surface.
Nf710 (talk) 10:58, 19 November 2015 (UTC) Where is your IRC?
In order to find the activation energy (to be compared with experimental data), the boat and chair transition structures are reoptimised at a higher level (DFT - B3LYP/6-31G*) for greater accuracy, and frequency calculations were also run. For each transition state (chair and boat), both the geometries (point groups) and energies differ before and after higher level optimisation (i.e HF/3-21G vs DFT - B3LYP/6-31G*).
| HF/3-21G | DFT - B3LYP/6-31G* | Experimental | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Structure | Chair TS
(Point group = C1) |
Boat TS
(Point group = CS) |
Reactant (anti2)
(Point group = C1) |
Chair TS
(Point group = C2h) |
Boat TS
(Point group = CS) |
Reactant (anti2)
(Point group = C2) |
Chair TS | Boat TS | |
| Electronic Energy (a.u) | -231.61932247 | -231.60280241 | -231.69260236 | -234.55693103 | -234.54307800 | -234.61179137 | N/A | N/A | |
| At 0 K | Electronic Energy + Zero-Point Energy (a.u)
(i.e Potential Energy at 0 K) |
-231.466700 | -231.450931 | -231.539601 | -234.414910 | -234.402352 | -234.469309 | N/A | N/A |
| ΔE (Potential Energy of TS at 0 K - Potential Energy of Reactant (anti2) at 0 K)
(i.e the activation energy via the chair or boat transition state of this reaction at 0 K) |
0.072901 Hartrees
= 45.7 kcal/mol |
0.08867 Hartrees
= 55.6 kcal/mol |
N/A | 0.054399 Hartrees
= 34.1 kcal/mol |
0.066957 Hartrees
= 42.0 kcal/mol |
N/A | 33.5 ± 0.5 kcal/mol | 44.7 ± 2.0 kcal/mol | |
| At 298.15 K | Sum of Electronic and Thermal Energies (a.u) | -231.461340 | -231.445302 | -231.532645 | -234.408982 | -234.396009 | -234.461976 | N/A | N/A |
| Sum of Electronic and Thermal Enthalpies (a.u) | -231.460396 | -231.444358 | -231.531701 | -234.408038 | -234.395065 | -234.461032 | N/A | N/A | |
| ΔE (Sum of electronic and thermal enthalpies of TS - sum of electronic and thermal enthalpies of reactant, at 298.15 K)
(i.e Activation energy of the reaction via either the chair or boat transition state, at 298.15 K) |
0.071305 Hartrees
= 44.7 kcal/mol |
0.087343 Hartrees
= 54.8 kcal/mol |
N/A | 0.052994 Hartrees
= 33.3 kcal/mol |
0.065967 Hartrees
= 41.4 kcal/mol |
N/A | N/A | N/A | |
These energies show that the 'boat' transition state is higher in energy (less stable) and hence the chair transition state is favoured.
Comparing the activation energies computed to the experimental activation energies for both the chair and boat transition states, it is clear that the values computed from the DFT - B3LYP/6-31G* level is much closer to the experimental values and hence more accurate.
Nf710 (talk) 11:10, 19 November 2015 (UTC) Your electronic energies are correct (pretty much) but your acrivation energies are abit out. But in general this table is laid out well and easy to read and most of the values are correct.
Nf710 (talk) 11:10, 19 November 2015 (UTC) In general this report is below average. you have missed out some crucial things such as IRC and frequency checks. You also didnt show any understanding of the theory and methods behind the computations we have used.
Exercise: Diels-Alder Cycloaddition Reaction (using AM1 semi-empirical molecular orbital method)
Diels-Alder Cycloaddition Reaction between Cis-butadiene and ethene
Cis-butadene
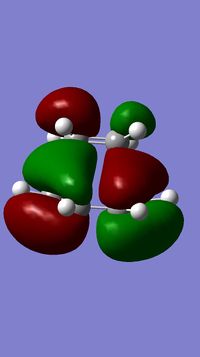
After constructing cis-butadiene on Gaussview, the structure was optimised using the AM1 semi-empirical molecular orbital method. The HOMO and LUMO of the molecule were then visualised (see below).
Transition state of the Diels-Alder Cycloaddition Reaction between cis-butadiene and ethene
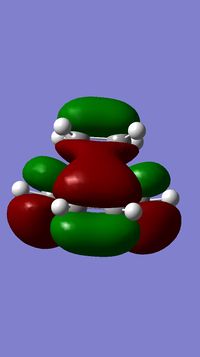
A guess for transition state of the Diels-Alder Cycloaddition Reaction between cis-butadiene and ethene was built and optimised using the AM1 semi-empirical molecular orbital method (opt+freq). The result from this computation was a structure that has just one imaginary frequency - this corresponds a transition state, which is what we are looking for. The diagram below shows the computed transition state with a point group of Cs:
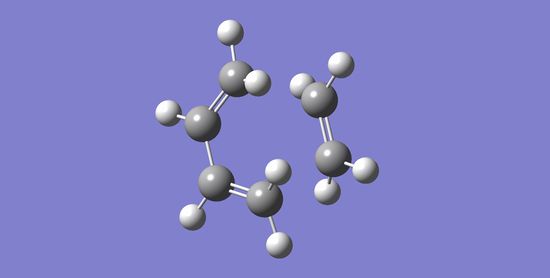
For each (of the two) partially formed C-C sigma bonds in this transition state. the 'bond' length is 2.12 Å. Typical bond lengths for sp3 and sp2 C-C bonds are 1.54 Å and 1.34 Å respectively[1], while the van der Waals radius of a C atom is 1.85 Å[2]. The distance between the carbons of the partially formed C-C sigma bonds are larger than typical sp3 bondlengths, implying the approach of the two components in the transition state the two components as the bond forms. This distance is also shorter than twice the van der Waals radius of a C atom, which reflects the interaction between the two carbons towards bond formation.
(Slightly confusing paragraph, but what you've written is fine Tam10 (talk) 16:26, 12 November 2015 (UTC))
For this obtained transition state, two vibrations, the one with the imaginary frequency and the one with the lowest positive frequency, were visualised. These are shown below.
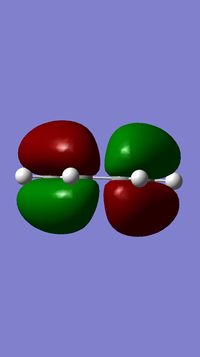
The HOMO and LUMO of this optimised transition state structure were also visualised. They are shown in the table below.
| HOMO | LUMO |
|---|---|
|
This MO is antisymmetric with respect to the plane cutting through the middle. |
This MO is symmetric with respect to the plane cutting through the middle. |
This cycloaddition reaction involves 6π-electrons. Systems with [4n+2]π electrons are thermally allowed only if the symmetry of both substrates involved in the cycloaddition are the same (symmetric or antisymmetric).[3] Based on this, since the HOMO of the transition state is antisymmetric with respect to the plane of reflection, the MOs involved in bond formation in this reaction should also be antisymmetric. This would correspond to the HOMO of cis-butadiene and the LUMO of ethene (both antisymmetric).
(It would be good to include the MOs of ethene to help demonstrate this Tam10 (talk) 16:26, 12 November 2015 (UTC))
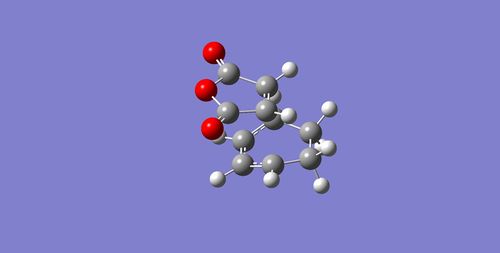
Diels-Alder Cycloaddition Reaction between Cyclo-1,3-hexadiene and Maleic Anhydride
The exo and endo transition states for the Diels-Alder Cycloaddition Reaction involving cyclo-1,3-hexadiene and maleic anhydride were found by optimising cyclo-1,3-hexadiene and maleic anhydride separately and then orienting them to look like the exo and endo transition states, followed by final optimisation using the Frozen Coordinate Method. (All calculations were done using the AM1 semi-empircal molecular orbital method.) The table below gives the information for the two transition states found.
The difference in energy of the two transition states, converted from Hartrees, is 2.85 kJ mol-1.The exo transition state is higher in energy than the endo transition state.
(This value could also go in the table above. But it's good that you've converted it to a relatable unit Tam10 (talk) 16:26, 12 November 2015 (UTC))
To compare the sterics of both transition states, the through-space distance between the -(C=O)-O-(C=O)- fragment of maleic anhydride and the nearest carbon on the same face of the molecule were measured, and are shown in the table below:
| Measurement | Distance (Å) |
|---|---|
| EXO TS:
Through-space distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2- |
2.94 |
| ENDO TS:
through-space distance between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH=CH- |
2.89 |
Without considering electronic effects, based on the structure of the exo and endo products, this distance is expected to be greater in the endo transition state (see diagram below).
(It could be easier to describe the above with some diagrams Tam10 (talk) 16:26, 12 November 2015 (UTC))
However, the measured distances prove otherwise, suggesting that there is a greater extent of favourable interaction between the two substrates (maleic anhydride and hexadiene) in the endo transition state. This explanation is supported by the lower energy of the endo transition as calculated above (which corresponds to a lower activation energy for the cycloaddition reaction via this transition state) compared to the exo transition state. The secondary orbital interaction between the pi orbitals of the maleic anhydride and cyclohexadiene substrates that is only possible in the endo transition state accounts for this.
References
- ↑ http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html
- ↑ Chemwiki.ucdavis.edu, (2013). Covalent Bond Distance, Radius and van der Waals Radius - Chemwiki. [online] Available at: http://chemwiki.ucdavis.edu/Theoretical_Chemistry/Chemical_Bonding/General_Principles_of_Chemical_Bonding/Covalent_Bond_Distance,_Radius_and_van_der_Waals_Radius [Accessed 5 Nov. 2015].
- ↑ Clayden, J. (2001). Organic chemistry. Oxford: Oxford University Press.