Rep:Mod:7401041994

Pericyclic reaction are described as a concerted reaction with a cyclic transition state. Probably the most well known pericyclic reaction is the Diels-Alder reaction. Using Gausview the transition state structures of the Cope Rearrangement and Diels Alder structures where investigated. It was possible to predict activation energies for the chair and boat transition state for the cope rearrangement and found that the boat TS has the highest activation energy. Investigation of the Diels-Alder between cyclohexadiene and maleic anhydride revealed that although the exo product is expected to have the highest energy transition state it actually has a lower energy transition state than the endo product, when using the DFT theory, and that there must be some secondary orbital effects in the endo product, confirmed using the AM1 semi-empirical theory, for it to be the major product.

Introduction

Cope Rearrangement

Image 1: Woodward-Hoffman analysis of the cope rearrangement

The Cope Rearrangement is a [3,3] Sigmatropic rearrangement. This means there is three carbon atoms on both sides between the sigma bond breaking and the new sigma bond forming. For the reaction to be thermally activated the Woodward-Hoffman rules says that only reactions with the total number of (4q+2)_s and (4r)_a components equal 0 or an uneven number are allowed. This limits the number of ways that the orbitals can line up and the reaction can progress. One of the ways is shown in Image 1. In this example the sigma bond and the left hand pi bond is antarafacially, and the right handed pi bond is suprafacially. This results in there being one (4q+2)_s component and no (4r)_a component and thus the reaction is allowed. Even with this limitation there are still multiple possibilities that the reaction can progress by. The two possibilities studied here are both concerted reaction either via a chair or a boat transition state. The reaction scheme is shown in Image 2 bellow

Image 2: Reaction Scheme for the cope rearrangement

Nf710 (talk) 10:25, 21 January 2016 (UTC) very good understanding of the stereo electronics and mechanistic properties

Diels-Alder

Image 3: WH analysins of the Diels-Alder Reaction

The Diels Alder reaction requires two components, a diene and a dienophile. The simplest Diels-Alder reaction is between a molecule of ethene and a molecule off butadiene. In this reaction the ethene acts as the diene and butadiene acts as the dienophile.

Image 4: Allignment of reaction resulting in different Transition states and products

The same Woodward-Hoffman rules apply to this reaction that apllies to the cope rearrangement. Image 3 shows a possible alignment of orbitals, where the ethene pi orbital react suprafacially and the two pi orbitals on the butadiene reacts antarafacially. This results in the same result as above and thus the reaction is thermally allowed.

As both ethene and butadiene is symmetrical the transition state for their specific Diels-Alder is very simple and does not allow for very interesting analysis. Although the transition states for more complex components result in more interesting analysis.

The reaction of Cyclohexadiene with Maleic Anhydride can go via two different transition states. The first one comes about when the O=C-O-C=O section of the maleic anhydride is beneath the $\pi$ system of the cyclohexadiene, this arrangement results in the product know as the endo adduct. The second transition state comes about when the O=C-O-C=O section of the maleic anhydride is pointing away from $\pi$ system of the cyclohexadiene i.e is under the single bond.this arrangement results in the product known as the exo adduct. These orientations are further illustrated in Image 4.

Computational Theory

Different mathmatical theories was used to do the calculations. The lower level Hartree-Fock which was mainly used to quickly optimise the structures and transition states before using the higher level Density Functional Theory (DFT) calculations, which generate more accurate results. The difference between the two theories is the Hamiltonian and basis set that is used to calculate the Schrodinger Equation.

$\hat{\mathit{H}}\mathit{\psi }=\hat{\mathit{E}}\mathit{\psi }$

The Hamiltonion ($\hat{\mathit{H}}$) is defined by the theory chosen to do the calculation and the basis set ($\mathit{\psi }$) can be changed based on how accurate the results has to be. The basis set defines the type of atomic orbitals that will be used in the calculations. The more atomic orbitals used the higher is the accuracy of the results generated by the calculation, but it will also increase the difficulty and thus the time it takes to complete the calculation.

The semi-empirical AM1 method was also used in the last part to generate a more complete MO diagram.

Nf710 (talk) 10:40, 21 January 2016 (UTC)Good intro, DFT is better in this case because you are using a higher basis set, however ab initio methods based on HF (but more complicated) are more accurate

Hartree-Fock

There are five main assumptions made by this method.

• Brorn-Oppenheimer approximation
• Mean field Approximation
• The calculations are done without considering any special relativity effects (not especially important as no work was done with heavy atoms)
• The variational solution assumed as a linear combination of a finite amount of basis sets.
• Energy eigenfunctions are described by only one slater determinant.

Any trail wave function used in the calculation of the time-independent wave function, which is used in this theory, will always have a energy of equal to or larger than the true ground state wave function and thus this method will just calculate an upper limit for the energy of the molecule.

Nf710 (talk) 10:48, 21 January 2016 (UTC) great understanding of the variation principle

DFT

It works on the assumption that the energy of an electronic system can be written in terms of the electronic probability density.

The two Hohenberg-Kohn theorems are central to the DFT calculations.

The first H-K theorem shows that the properties of a many electron system in the ground state can be determined by an electron density that depends on only 3 spatial co-ordinates instead of 3N (Where N is the amount of electrons). The second defines an energy functional (function of a function) for the system and proves that the ground state electron density minimises the energy funtional.

The theory also models electrons as moving in an effective potential instead of interaction with each other. The simplest way of doing this is the local-density approximation. This approximation is based on using exact exchange energy for an uniform electron gas. This can be obtained using the Thomas–Fermi model

Semi-empirical AM1

This method is based on the Hartree-Fock method. The only difference is that it makes a lot more approximations and obtains some of its data from empirical data.

Basis Sets

The 3-21G and 6-31G* basis sets where used to do most of the calculations. The 3-21G was used with Hartree-Fock and the 6-31G* with DFT. These basis sets are known as split-valence basis sets. Split-Valence basis sets focus more on the valence shell of the molecule and thus uses more equations to describe it and less to describe the inner shells. The first number (3/6) is the number of Gaussian equations ($f(x)=a{e}^{\frac{(x-b{)}^2}{2c^2}}$) summed to describe the inner shells. The second two numbers (21/31) is the number of Gaussian functions that are are used to describe the first and second STO's in the double zeta respectively. The double zeta allows for each orbital to be accounted for separately, resulting in a more accurate representation of the orbitals. In the double zeta each orbital is defined by 2 Slater Type Orbitals (STO's) which are orbitals that posses exponential decay at long range and their generalised coulomb potential has a cusp at the atom nucleus. The only difference between the 2 orbitals used are their size (defined by the parameter ζ). The STO's will also not be added to one another 1 to 1. The second one will always have a factor that acts upon it before they add together. The * takes into account the fact that the orbitals change upon them interacting and polarises the atomic orbitals.

Nf710 (talk) 11:13, 21 January 2016 (UTC) fantastic underdstanding

Cope Rearrangement Tutorial

Optimising products and reactants

Image 5: Energy vs Dihedral angle of central 4 carbon atoms.(Generated by ChemBio3D Ultra 2014

Using ChemBioDrawPro 2014 Image 5 can easily be generated. Image 5 is a plot of energy against the dihedral angle of the central 4 carbons. From this it is possible to see that due to the rotation around the central bond of 1,5-hexadiene there is multiple possible conformations that it can take and they each have an energy associated with them. The plot shows the lowest energy conformation is formed when there is an 180^o angle between the two vinyl groups, these conformers are know as antiperiplanar conformers. Also when there is a 0 degree angle the energy is at its highest. There is also two low points at about ±60^o corresponding to the Gauche conformers.

The cope rearrangement can only happen when the molecule is in a specific orientation where all the orbitals are line up at the same time. Such as the one shown in the introduction, which has the dihedral angle at 0^o.

The table below details the results gained from the calculations done on the different conformers of 1,5-hexadiene

Part	Conformation	Energy	Point Group	Jmol Structure	Structure from script table
a	Antiperiplanar	-231.68907065 a.u	C2h	Structure	Anti3
b	Gauche	-231.69166698 a.u	C2	Structure	Gauche2
c	Gauche	-231.69266122 a.u	C1	Structure	Gauche3
e	Antiperiplanar	-231.69253525 a.u	Ci	Structure	Anti2
f	Antiperiplanar	-234.61171166 a.u	Ci	Structure	Anti2

Rerunning the structure from e at the higher level DFT causes a small change is bond angle and lengths. The general structure stays the same but the point group changes to C_2h.

Image 6: Steroelectronic interaction between pi systems

Contrary to what has been discussed above, the Gauche conformer turns out to be the lowest energy conformer. This is because the graph above only considered the sterics of the molecule. Once the electronics of the system is considered the result above is immediately clear. There is a stereoelectronic interaction between the two pi bond structures resulting in the lowering in energy of the whole mollecule. This is shown in image 6. This results in two competing interactions in this conformation. Sterically the two biggest groups want to antiperiplanar to each other as shown by the graph. Electronically the two pi structures want to be next to each other to maximise the overlap. Too be in the lowest energy conformer the molecule limits the steric clash while still getting as much overlap as possible between the two pi systems. This results in the structure shown.

Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal enthalpies	Sum of electronic and thermal free energies
-234.469215 a.u	-234.461866 a.u	-234.460922 a.u	-234.500800 a.u

The data in the table above is for molecule e/f and shows the electronic energy of the molecule with some corrections applied for various factors. The first one is the potential energy at 0K plus the zero point vibrational energy. The second one is the energy at rtp and including contrabutions from rotational, vibrational and translational motion. The third one has an extra correction for RT. Fourth has a extra entropic contribution to the Gibbs free energy.

Nf710 (talk) 11:47, 21 January 2016 (UTC) Excellent use of the orbitals to explain the ordierng inn energy and well done for using chem bio for showing how the energy changes with bond angle. You havent shown that there are no imaginary frequencies however.

Optimising Transition States

Image 7: Reaction vibration

Allyl fragments (CH₂CHCH₂) were optimised and then used to generate a guess structure for the transitions state. Using different methods transition state structures where optamised in either the boat or chair conformation.

Starting with a chair conformation guess structure it was optamised to a TS(Berry) using the Hartree-Fock method. At first the guess structure was not lined up correctly and the resultant imaganary frequency was -537.28 Hz instead of the expected 818 Hz. After lining up the structure a bit more the expected result was achieved. And the vibration corresponds to the rearrangement reaction as shown in Image 7.

Next the same guess structure was used but this time the bond distances between the terminal carbons of the fragments where frozen and the rest of the structure was then optimized. After the optimisation was completed the same bonds that was frozen where optamised. This was done using a Hessian matrix to describe the curvature of the reaction coordinates in both directions.

Nf710 (talk) 11:53, 21 January 2016 (UTC) The above sentence does make sense. the hessian is matrix of force constants used to determine the nature of a stationary point

Optamisation Method	Bond Making Distance (Å)	Bond Breaking Distance (Å)	Energy (a.u)	Internal Angle (o)	TS Structure
TS(Berry)	2.02050	2.02030	-231.61932245	120.50313 and 120.50568	Chair
Redundant Coordinates	1.98458	1.98429	-234.57196121	120.16408 and 120.16417	Chair
QST2	2.14032	2.14014	-231.60280238	121.67851 and 121.67854	Boat

Image 8: Boat TS generated by QST2 method

The general structure of the TS from both calculations are the same with just a few small differences as detailed in the table above. The bond making and breaking distances shows that the transition state is not perfectly symmetrical with the distance between the carbons forming the new bond being slightly longer (This is deduced from the IRC calculation that will be detailed later). This suggest that the transition state is slightly more towards the reactants than towards the products. As the reactants and products are the same the overall reaction energy is 0 and the transition state will be expected to be symmetrical in the center of the reaction coordinates.

The QST2 method uses the optamised structure of hexadiene from (f) above as a starting point and then re-numbering the atoms to correspond to their position in the product. From this it is possible to get Gausian to calculate the TS without having to submit a guess structure. The two main differences between the structure resulting from this method and that resulting from the other two methods, is that it has a boat structure and has a longer distance between the terminal carbons. The increased bond length is most likely resultant from the steric clash between the 4 axial hydrogen's. The structure is shown in Image 8 where the axial hydrogen's can be seen.

Nf710 (talk) 11:55, 21 January 2016 (UTC) You havent given the frequency that you got to prove it is a TS

Image 9: IRC calculation results

Even though the transition structures has been found it is difficult to know from which hexadiene conformer it originated. Using an IRC calculation it is possible to go forward or backwards or both ways from the transition state structure to find the reagent or product structure. With the cope rearrangement having the same reagent and product it doesn't matter which way the calculation is taken. The output of the calculation is shown in Image 9. From this it can be seen that the conformer that the reaction proceeds to is the Gauche3 conformer (Structure). The Gauche3 conformer is the lowest energy conformer so it is expected that the reaction would procede till it reaches the lowest point.

Nf710 (talk) 11:57, 21 January 2016 (UTC) It goes to gauche 2 you can see this if you look down the middle bond in your Jmol of the IRC also you should ahve included the drawing

The activation energy is the energy difference between the reactants and the transition state. After optamising the transition states at the higher level DFT theory the activation energies for both transition structures were calculated and is detailed in the table below.

TS Structure	TS Energy (-a.u)	Reactant Energy (-a.u)	Difference (a.u)	Calculated Activation energy (kcal/mol)	Experimental Activation Energy (kcal/mol)
Boat	234.54307904	234.61171166	0.06863262	43.067	44.7 ± 2.0
Chair	234.55693104	234.61171166	0.05478062	34.375	33.5 ± 0.5

The activation energy for the chair TS might not be inside the experimental range but it is very close and shows that the calculation was successful.

Nf710 (talk) 11:58, 21 January 2016 (UTC) You have barley explained this.

Nf710 (talk) 12:04, 21 January 2016 (UTC) You are clearly very intelligent. Your understanding of the theory is very high and I have awarded you for this. But you should have followed the lab script, especially when wiring up, it was a bit all over the place and difficult for me to get through. you have missed out geometry comparisons and haven't put down frequencies etc. I have awarded you highly for your knowledge of theory but you missed out a few things so i couldn't give you some of the marks there. However you should consider doing computational chemistry as you seem to have a good understanding of the concert.s

Diels Alder Cycloaddition

Butadiene and Ethene

Image 10: HOMO for Butadiene	Image 11: LUMO for Butadiene
Image 12: Lumo of ethene	Image 13: HOMO of TS

(Where's the TS LUMO? Tam10 (talk) 11:22, 12 January 2016 (UTC))

As discussed above the simplest Diels-Alder reaction is between ethene and butadiene. Using the AM1 semi-empirical calculations the molecular orbitals for butadiene and ethene were calculated. From images 10 and 11 it can be seen that both the HOMO and LUMO are asymmetric with respect to the plane of the molecule but symmetrical with respect to the plane bisecting the single bond. Both the HOMO and the LUMO of the butadiene molecule has the right symmetry to interact with the LUMO and HOMO ($\pi$ and $\pi$^* orbitals) of the ethane molecule respectively.

("both the HOMO and LUMO are...symmetrical with respect to the plane bisecting the single bond" - the HOMO is antisymmetric wrt the plane bisecting the single bond Tam10 (talk) 11:22, 12 January 2016 (UTC))

Image 14: WH analysis

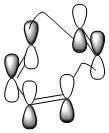
Calculating the MO's for the transition state structure shows that the HOMO of the butadiene interacts with the LUMO of the ethene(Image 12). The structure also shows the angle of aproach to be 102.24⁰ which is relatively close to the Burgi-Dunits anngle of approach. The bond length between the carbons forming the bonds are 227.216 and 227.217 pm. The normal bond length between two sp² carbons are 147 pm and between two sp³ carbons are 154 pm and the Van der Waals Radius of a carbon atom is 170 pm. The partially formed bond lengths are larger than the bond length of a single bond but still smaller then two times the Van der Waal's radius (340 pm). This suggests that the transition state lies more towards the reactants than the products. This can also be seen from the HOMO of the TS (Image 13) which looks a lot like the individual MO's of the reactants. The energy for the transition state was calculated to be -234.54388554 a.u and for butadiene and ethene to be -155.98595128 a.u and -78.58745864 a.u respectively making the activation energy 18.53 kcal/mol.

The imaginary frequency corresponding to the reaction show synchronous bond formation. The carbons stretch towards each other while the hydrogen's bend away from each other. Comparatively the lowest real frequency vibration is just a twisting of the ethene molecule.

(What was the value of these frequencies? You should also have illustrated them Tam10 (talk) 11:22, 12 January 2016 (UTC))

Using the orientation at which the orbitals interacts as described above the system has one 2$\pi$_s and one 4$\pi$_s component resulting in an allowed reaction based on the Woodward-Hoffman rules.

The above reaction is between two symmetrical molecules, the orientation with which they approach each other has no effect on the resulting product. When more complex molecules are used the orientation with which they approach each other is more important in the stereo- and regio-chemistry of the molecule. One such reaction will be studied below between Cyclohexadiene and Maleic Anhydride.

Cyclohexadiene and Maleic Anhydride

Error creating thumbnail: File with dimensions greater than 12.5 MP Image 15: Possible secondary orbital overlap	Error creating thumbnail: File with dimensions greater than 12.5 MP Image 16: Secondary orbital overlap
Image 17: Possible steric clash in the exo TS

Image 19: IRC calculation showing that moving forward from TS structure results in the product expected

(This code is perhaps a little inefficient. You're reloading the file every time the script loads Tam10 (talk) 11:22, 12 January 2016 (UTC))

As mentioned above there is two possible transition states for this reaction based on the orientation of the maleic anhydride. Depending on the orrientation either the endo or the exo product will be formed. The reaction is kinetically controlled and the Alder rule states that the endo product will be the major product. Thus it is feasible to suspect the transition state resulting in the endo product to be lower in energy.

Although the energies ( -612.69630939 a.u for the exo TS and -612.68336524 a.u for the endo TS) suggests that this is not the case, and would suggest that the exo product should be the major product.

Looking at the LUMO of the endo TS reveals the possibility that the $\pi$ orbital on the oxygen can interact with the $\pi$ system in the maleic anhydride. Although it might not have been calculated properly as there is no actual electron density on the Oxygen but just some peaks extending towards it, which can be seen in Image 15. The assumption can be made that when this interaction is accounted for properly in the final energy calculations the endo TS will be lower in energy than the exo TS.

This is confirmed when using the AM1 semi-empirical method to run the calculations again, giving the energies as -0.05041982 a.u and -0.05150481 a.u for the exo and endo form respectively. Image 16 shows the orbital overlap in the LUMO.

Comparing the structure of the two transition states shows that there is very little structural differences between the endo and the exo form apart from the orientation of the maleic anhydride. The only other notable difference is the distance between the bond forming carbon atoms (228 pm for exo and 226 pm for endo). This is most likely due to the strain caused in the system due to the steric clash between the -(C=O)-O-(C=O)- of the maleic anhydride and the hydrogen's on the sp3 carbons of the cyclohexadine, as shown in image 17. There is no/very small differences in the bond lengths of the other bonds and the angle of approach is also very similar.

(What were the actual differences between the side-groups and how did they compare to the combined VdW radii? Tam10 (talk) 11:22, 12 January 2016 (UTC))

The exo form experiences more strain than the endo form. This should mean that it will be higher in energy than the endo form even without the secondary orbital overlap consideration. There is only a few factors that affect the overall energy of the molecule. Based on the level of theory that is used different once will be accounted for and the higher the level of theory the more factors are accounted for. Some of the main factors are the energy of the molecular orbitals, any strain in the molecule and the dipole moment or charge separation. Thus too see why then endo form might still be higher in energy the dipole moment has to be investigated. The dipole moments are 6.1140 D for the endo form and 5.5493 D for the exo form. The larger the dipole moment the higher the energy thus this explains why the endo form is once again higher in energy than initially expected.

From the images it can be seen that the orbitals on the oxygen's outside the ring has the right orientation and phase to be able to interact with the pi system as well. This could lead to a further stabilisation of the endo TS.

Conclusion

It has been shown that due to secondary orbital overlaps the gauche conformer has a lower energy than the antiperiplanar conformer. The boat transition structure has been shown to be the lowest in energy for the cope rearrangement. The investigation of the Diels-Alder reaction between ethene and cyclobutadiene did not result in anything unexpected but was a good introduction into the theory and computational methods. The reaction between Maleic anhydride and Cyclobutadiene resulted in a more intresting system to investigate. With the DFT theory generating the relative energies of the endo and exo forms wrongly, suggesting that the exo form will be the major product. The error was rectified when using the AM1/SE calculation which took the secondary orbital overlap into account and generated the correct relative energies.