Rep:Mod:61ntmod3

Transition States and Reactivity

The Cope Rearrangement

Introduction

The Cope Rearrangement is often seen as the model example of a [3,3]-sigmatropic shift. This characterisation is based on modern research in the field of pericyclic reactions, which now widely accepts that the rearrangement of 1,5-hexadiene occurs via a concerted mechanism:

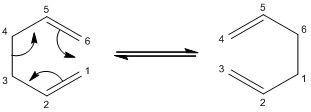
Without labelling the carbon atoms, the reactant and product are identical; the choice of mechanistic pathway can only be rationalised through studying the structures and energies of possible transition states. In particular, these have been found to resemble the chair and boat geometries of a cyclohexane ring. It is possible to simulate and compare these geometries using computational methods and thus gain a deeper understanding of the likely kinetics of the reaction. Thermodynamic information may also be obtained through modelling the most stable conformations of the reactant and product.

The Reactant and Product

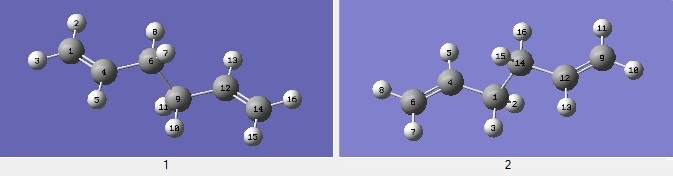
The first conformation of 1,5-hexadiene to be optimised was one which supported an anti linkage about the four central carbons. The Hartree-Fock method with a 3-21G basis set was chosen for its speed and the molecule was deemed simple enough for this to provide satisfactory results.

The results show that this conformer has an energy of -231.69260 a.u. (arbitrary units in hartrees; -145389.193 kcal mol^-1) and its point group is C₂. This corresponds to the first anti structure in the reference table: https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3.

However it will be demonstrated that this is not the most thermodynamically stable conformer. Another molecule of 1,5-hexadiene was reconstructed with a gauche linkage about the central four carbons with the following output:

Energy: -231.69266 a.u. (-145389.230 kcal mol^-1). Point group: C₁. This is the third gauche conformer in the reference table.
It was expected that the anti conformer would be more stable given that the 180^o dihedral angles appear optimal to avoid steric clashing of the C=C double bonds at either end of the molecule. However extra H-H van der Waals' stabilising interactions are found in the gauche conformer between the each of the hydrogens of non-neighbouring carbon atoms (within the sum of their van der Waals' radii; approximately 2.1-2.4 Å). Also a gauche rotamer will be entropically favoured given that there are six possible conformers with this linkage and only four such anti conformers. Incidentally, these two featured conformers are the lowest energy examples of the anti and gauche-type linkages within 1,5-hexadiene. Therefore the gauche conformer above is the overall lowest energy conformer for this molecule.

The next conformer to be investigated (using the same method and basis set) had an anti linkage and belonged to the C_i point group:
Energy: -231.69254 a.u. (-145389.154 kcal mol^-1).
This result was then optimised using the B3LYP method and 6-31G* basis set:
Energy: -234.55824 a.u. (-147186.915 kcal mol^-1).
The lower output energy reflects the increased accuracy of the method chosen. Although the C_i point group has not changed, certain structural parameters are adjusted; the C=C bonds increased from 1.32 Å to 1.34 Å and the central C-C bond increased from 1.55 Å to 1.56 Å. The other C-C bonds remained the same but the C=C/C-C dihedral angles increased from 115^o to 119^o.

To confirm the success of the optimisation, a frequency analysis was carried out. The spectrum obtained is given below:

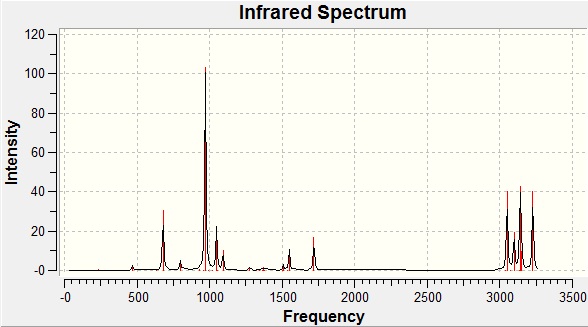
Figure 2: The computed infrared spectrum of the anti2 conformer

The energy and point group were retained, thus the frequency analysis did not interfere with the structure of the molecule. The fact that there are no negative frequencies (i.e. turning points) reported confirms that the optimisation to an energy minimum was successful. The C=C stretch shown at 1728 cm^-1 is above the literature range of 1630-1680cm^-1 for this functional group but this is to be expected given that the simulation is solventless.

The table below lists a summary of the thermodynamic properties computed during the analysis:

Energetic Contributions

Type	Energy/hartrees	Energy/kcal mol-1
Eelec + ZPE	-234.41624	-147098.298
Etrans + Evib + Erot	-234.40895	-147093.723
H = E + RT	-234.40800	-147093.130
G = H - TS	-234.44786	-147118.139

The first term is the sum of the electronic and zero point energies, which represents the potential energy at 0K or the zero point vibrational energy. The second is the total energy at 298.15K and 1 atm pressure as a sum of the translational, rotational and vibrational degrees of freedom. The third is an additional correction to RT by accounting for the electronic and thermal enthalpies. The last term is the entropic contribution to the total free energy as a sum of the electronic and thermal free energies.

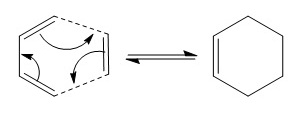
The Chair and Boat Transition States

It was previously mentioned that the transition state for the Cope Rearrangement can take the form of a chair or boat. These theoretical structures can be modelled and thus derived using computational methods as well as then being used to simulate possible reaction pathways from the reactant to the product.

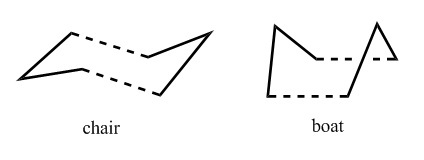
As the image above shows, they are similar in that they are both comprised of two allyl fragments. Therefore to begin their construction, this fragment must be created and optimised. At the HF/3-21G level of theory, the following results were obtained:

• Energy: -115.82304 a.u. (-72680.000 kcal mol^-1)
• Point group: C_2v

The successful convergence of this optimisation is sufficient to duplicate and combine to model the transitions states. Two methods of optimising the chair geometry were investigated: computation of the force constant matrix (the Hessian) or freezing the reaction coordinate, minimising the molecule then unfreezing the process and so on. This is slower but a more reliable method for instances where the initial guess is not good enough to converge at the first stage. For the force constant matrix calculation, the extra command "Opt=NoEigen" was input to prevent the failure of the calculation when more than one imaginary frequency is detected. The force constants were just calculated once. The length between the terminal carbons on the two allyl groups was guessed at 2.20 Å. The HF/3-21G method was used again to optimise to a TS (Berny method) as well as compute the frequencies at this minimum give the following structure:

• Energy: -231.61932 a.u. (-145343.209 kcal mol^-1)
• Point group: C_2h
• Length of bonds forming/breaking: 2.02 Å
• Imaginary frequency: -818 cm^-1

The imaginary frequency corresponds to the stretches about the frozen transition state; as the figure above shows, this resembles the bond formation/breaking vibrations of 1,5-hexadiene.
The frozen coordinate method produced an almost identical output based on freezing the terminal carbon atoms at the same fixed distance of 2.20 Å then optimising these "bonds". The frequency calculation was performed during the second stage involving the Hessian, although the force constants were not calculated:

First step-

• Energy: -231.61519 a.u. (-145343.209 kcal mol^-1)
• Point group: C_2h
• Length of bonds forming/breaking: 2.20 Å

Second step-

• Energy: -231.61932 a.u. (-145343.209 kcal mol^-1)
• Point group: C_2h
• Length of bonds forming/breaking: 2.02 Å

The boat transition state is inherently less stable than the chair due to a higher degree of torsional strain. Thus an entirely different method was used to obtain this structure. The anti2 reactant from an earlier optimisation was duplicated and its atoms were re-labelled to represent the product molecule.

The QST2 method (under HF/3-21G) tried to interpolate the transition state based on these initial and final species but failed to converge because the product and reactant conformations are not close enough to the geometry of the transition state. Thus alterations were made to the central dihedral angle and the internal C-C-C angles; these were set to 0 and 100^o respectively.

This converged to the expected boat structure with the following parameters:

• Energy: -231.60280 a.u. (-145332.843 kcal mol^-1)
• Point group: C_2v
• Bond forming/breaking: 2.14 Å.
• Imaginary frequency: -840 cm^-1

Now that the transition states have been characterised, a new question is raised as to which conformers follow either of these pathways. Such a problem may be solved using the Intrinsic Reaction Coordinate (IRC) method, which traces the minimum energy pathway in a stepwise fashion from a transition state to its local energy minima. If calculated in both directions, this will lead to the original reactant and product molecules. The strategy will be demonstrated for the chair transition state of the Cope Rearrangement. Since the pathway of this reaction is symmetrical, the calculation need only be computed in one direction. For the initial IRC analysis, the force constants were only computed once and the number of points along the coordinate was set to 50. The calculation to this point was incomplete because the input was not sufficiently detailed. Three improvements were applied separately: i) the final point of the calculation was optimised to a minimum; ii) the initial input was increased from 50 points to 100 and; iii) the force constants were recomputed at every step. All three methods achieved successful outputs:

The incomplete result still resembles the chair transition state but the others correspond to the gauche2 conformation of 1,5-hexadiene; this is one of several low energy conformations and perhaps the nearest local minimum (as opposed to the overall lowest minimum at gauche3). It may be that this is the final conformation the molecule must go through before reaching the transition state and then passing through the same geometry towards the product. Other more stable states would then be accessible via thermodynamic control. For more complex calculations, it is worth noting that the first method is the fastest to compute. The second is slower and if given too many points, may be susceptible to locating the wrong energy minima, but it is overall more reliable than the first. The most reliable is the third method but this is the most expensive to compute.

The final pieces of information to be extracted from the transition states are the relative activation energies. This requires a further optimisation at the B3LYP/6-31G* in order to be comparable with the reactant structure confirmed in the previous IRC analysis. The results of this optimisation are as follows:

B3LYP/6-31G* Optimised TS parameters

Parameter	Chair	Boat
Total energy/hartrees	-234.50547	-234.49291
Total energy/kcal mol-1	-147154.291	-147146.414
Point group	C2h	C2v
Bond forming/breaking length/Å	2.03	2.25
Imaginary Frequency/cm-1	-562	-504

Therefore the activation energies at 298.15 K with respect to anti2 product and reactant conformations will be +32.62 and +40.50 kcal mol^-1 for the chair and boat pathways respectively. These compare very nicely with the experimentally observed energies of +33.5 ± 0.5 and 44.7 ± 2.0 kcal mol^-1 at 0 K.

Using the FreqChk program within Gaussian, these values may be recalculated at 0 K for better comparison. The new energies at this temperature are given below:

Parameters at 0 K

Parameter	Reactant	Chair	Boat
Total energy/hartrees	-234.27498	-234.36341	-234.35216
Total energy/kcal mol-1	-147011.545	-147045.149	-147056.089

This gives the new activation energies of +33.604 and +44.54 kcal mol^-1 which are much closer in agreement.

The Diels-Alder Cycloaddition

Much like the Cope Rearrangement, the Diels-Alder cycloaddition proceeds via a concerted, i.e. pericyclic mechanism. It is denoted [4+2] because one fragment has four π electrons and the other has two; two new σ bonds are formed while three π bonds are broken with a total of six electrons involved. The selection rules of the mechanism lead to high stereospecificity in the products and this may be rationalised by the structural and orbital symmetry features of the transition state.

Ethylene and cis-Butadiene

In the same way as for the Cope Rearrangement, the transition states of the reaction shown in the equation above. This time they demonstrate exo and endo isomerism; but for this simple case, where the reactants do not support functional groups, only one transition state exists. To begin estimating this species, the fragments have been drawn and optimised to the semi-empirical AM1 level, which is a much simpler but weaker approximation than those used previously. Hence this was followed up with the B3LYP/6-31G* method:

B3LYP/6-31G* Optimisation of the Reactants

Property	cis-Butadiene	Ethylene
Energy/hartrees	-155.95383	-79.04563
Point group	Cs	C2h
C=C length/Å	1.34	1.33

This level of accuracy was deemed sufficient to move on to looking at the molecular orbitals of these fragments. The HOMO and LUMO of each molecule are given below:

With respect to a vertical plane of symmetry down the centre of each of these MOs, the HOMO of cis-Butadiene (far left) and the HOMO of ethylene (second from right) can both be described as symmetric, s. The LUMOs are both antisymmetric, a, about this plane. These properties will be revisited as a reference for the transition state investigation.

The Transition State

Using the optimised fragments from the previous section, the transition state of this reaction can be modelled. The interfragment distance was guessed at 2.20 Å with an angle of incidence (of ethylene, with the butadiene fragment at zero) of 95^o. The AM1 and B3LYP/6-31G* outputs for this are given below:

Optimisation of the Transition State

Method	AM1	B3LYP
Energy/hartrees	0.11165	-234.49456
Point group	Cs	Cs
Bond forming length/Å	2.21	2.10
Angle of ethylene incidence/o	99	102

At the B3LYP level the frequencies were also computed. One imaginary frequency was found at -526 cm^-1. Both this vibration and that of the first real frequency are displayed below:
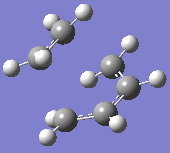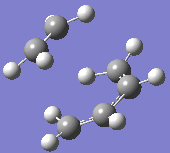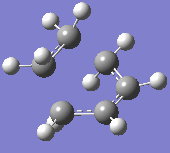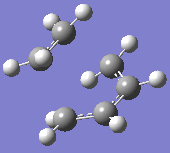
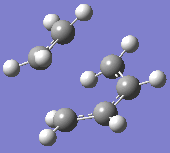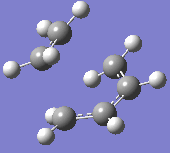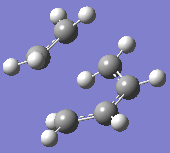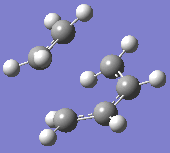
This proves that the correct transition state structure has been obtained: the negative frequency denotes a maximum turning point on the potential energy surface and physically, this demonstrates a vibration of synchronous bond formation and synchronous bond breaking between the fragments. The first real frequency is a simple twist and is not of the correct orientation for the same reactive effect.

The length between the fragments may be compared with the literature sp³ and sp² C-C bond lengths of 1.54 and 1.34 Å respectively. This tells us that bonds are not yet fully formed, but comparison with the sum of two carbon van der Waals' radii at 1.7 Å each, also indicates that partial bonding has occurred.

The HOMO and LUMO of this transition state were also computed:

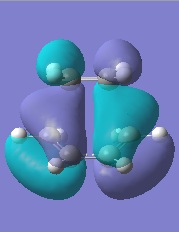
As the figure on the left demonstrates, the HOMO is antisymmetric about the virtual vertical plane down the centre of the transition state. It perfectly correlates with combination of the HOMO of cis-butadiene and the LUMO of ethylene. The LUMO is symmetric and the product of the cis-butadiene LUMO and the HOMO of ethylene. The selection rules dictate that orbitals of the same symmetry combine to produce the final MOs.

Regioselectivity in Diels-Alder Reactions

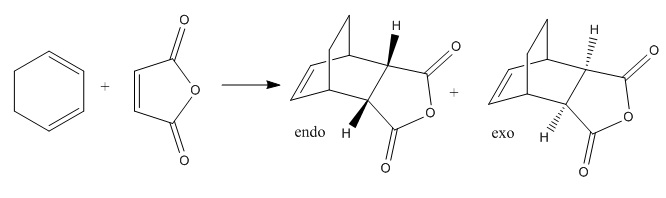
This famous example of the Diels-Alder reaction involves maleic anhydride and cyclohexa-1,3-diene leading to high selectivity for the endo isomer, which was, at first, surprising given that the exo isomer is more thermodynamically stable. By studying the orbitals of the transition state, it will become clear that a kinetic effect dominates the selectivity; in other words, the activation energy and not the overall energy change is the major reason for the observed yield.

The endo and exo transition states were approximated and optimised gradually (as before) to the B3LYP/6-31G* level from optimised fragments of maleic anhydride and the cyclohexadiene. The input and outputs of this are given below:

Optimisation of the Exo/Endo Transition States

Isomer	Exo	Endo
Energy/hartrees	-612.49098	-609.32100
Energy/kcal mol-1	-384343.603	-382354.409
σ bond forming length/Å	2.29	2.32
π bond forming length/Å	1.40	1.38
Maleic anhydride C=C length/Å	1.41	1.38
cis-butadiene C=C lengths/Å	1.40	1.41

Now it is clear that the exo transition state is of higher energy than the endo, therefore under kinetic conditions, the endo pathway is dominant due to a lower activation energy. Other features of the transition states may be compared; for example, the 3D structures show that the exo transition state is subjected to more steric hindrance as the large, electronegative oxygen groups of the maleic anhydride fragment approach over the sp³ centres of cyclohexadiene. This may impact the length of the forming σ partial bond as it is longer in the case of the exo isomer.

Simulations of the transition state imaginary vibrations for the exo and endo pathways were also obtained to confirm these optimisations:

exo endo

It is only by examining the molecular orbital interactions within these transition states that more illustration of the higher energy exo state may be shown. Below are the HOMOs of the exo and endo transition states:

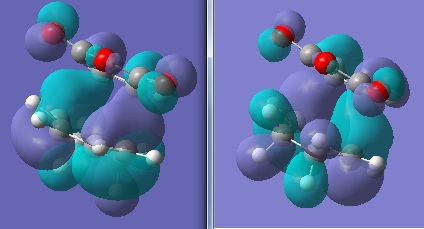
The exo (left) case has and extra node between the O=C-O-C=O part of maleic anhydride and the conjugated π system directly below it. In the endo case, there is a secondary orbital overlap between in-phase C-H bonding regions (on the sp₃ carbons and the anti-bonding regions on the oxygens of the carbonyl groups. Overall this stereoelectronic effect stabilises the endo transition state relative to the exo.

NB: These calculations do not take into account the effects of higher temperature or pressure which may lead to greater preference for the thermodynamic exo product.