Rep:Mod:479231
Transition states and reactivity
The aim of this project is to investigate two very important organic reactions using computational chemistry. These reactions are the Cope Rearrangement and the Diels Alder reaction. The software I will be using is Gaussian which uses quantum mechanics and the Born-Oppenheimer approximation in order to create potential energy surfaces. The surfaces plot the potential energy of molecules against the reaction co-ordinate and are very useful for calculatiing properties such as the optimum energy of molecules. In this particular project I will mostly be looking at transition states which can be found by carrying out frequency analysis's and finding negative vibrations.
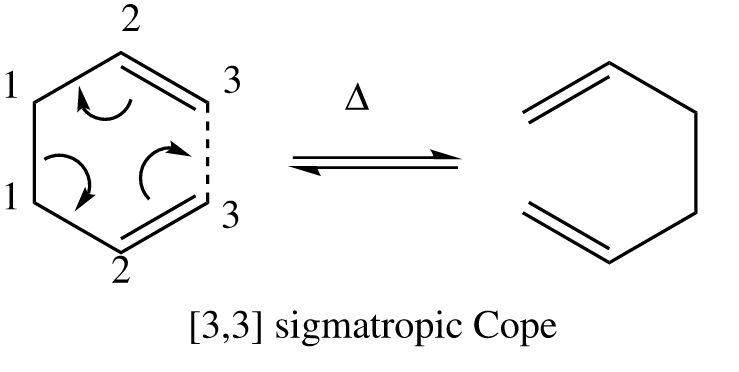
The cope rearrangement
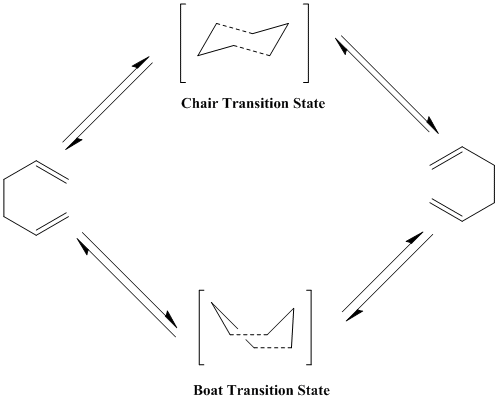
The cope rearrangement is a perycyclic reaction involving a [3,3] sigmatropic shift of 1,5-dienes. This reaction is reversible and requires heated conditions. It can proceed via a chair or a boat transition state.
Tha aim of this project is to investigate which of the two transition states this reaction goes through. It is known that the chair transition state is more stable then the boat transition state due to it having less steric hinderance.
Optimization of 1,5-hexadiene
Anti-peri planar
I initially optimized 1,5-hexadiene using a HF/3-21G level of theory. The structure was drawn in the anti-peri planar form in order to prevent it minimizing to a gauche structure. Details of the calculation are shown below:
File Type = .log Calculation Type = FOPT Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.68539585 a.u. RMS Gradient Norm = 0.00005236 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = CI Job cpu time: 0 days 0 hours 0 minutes 24.5 seconds
Item Value Threshold Converged?
Maximum Force 0.000121 0.000450 YES
RMS Force 0.000035 0.000300 YES
Maximum Displacement 0.001695 0.001800 YES
RMS Displacement 0.000522 0.001200 YES
Predicted change in Energy=-4.327992D-07
Optimization completed.
-- Stationary point found.
When the molecule was symmetrized the point group was to C2h. This shows that the molecule is the anti 3 conformer in accordance with the appendix[1] and an energy of -231.68540 a.u.
Gauche
The same molecule was then investigated but in a gauche conformation. The same method of calculation was used as previously.
File Name = gauche optimal structure File Type = .log Calculation Type = FOPT Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.68771611 a.u. RMS Gradient Norm = 0.00002452 a.u. Imaginary Freq = Dipole Moment = 0.4556 Debye Point Group = C1 Job cpu time: 0 days 0 hours 2 minutes 42.0 seconds.
test molecule |
D-Space optimised gauche structure
Item Value Threshold Converged?
Maximum Force 0.000057 0.000450 YES
RMS Force 0.000013 0.000300 YES
Maximum Displacement 0.001728 0.001800 YES
RMS Displacement 0.000447 0.001200 YES
Predicted change in Energy=-4.130760D-08
Optimization completed.
-- Stationary point found.
When the molecule was symmetrized it gave a point group of C2. The energy of the molecule is -231.68772 a.u and is in accordance with the gauche 1 conformer shown in the appendix[1]. This conformer is the highest energy of the gauche conformers. This is due to the steric hindrance of the two terminal carbons facing one another.
Optimized Gauche calculation
From the two calculation above you can see that the gauche conformation is lower in energy then the anti-peri planar conformation. As the appendix shows, there are multiple gauche conformations possible and in the next calculation I will try and optimize it so it has the lowest possible energy. The same calculation method was used as previously and the results are shown below:
File Name = 2nd calc gauche File Type = .log Calculation Type = FOPT Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.69266121 a.u. RMS Gradient Norm = 0.00000825 a.u. Imaginary Freq = Dipole Moment = 0.3409 Debye Point Group = C1 Job cpu time: 0 days 0 hours 1 minutes 22.2 seconds.
Item Value Threshold Converged?
Maximum Force 0.000014 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000905 0.001800 YES
RMS Displacement 0.000283 0.001200 YES
Predicted change in Energy=-1.179476D-08
Optimization completed.
-- Stationary point found.
The molecule was symmetrized and the point group was C1. This shows that the molecule is in the lowest energy gauche 3 conformer with an energy of -231.69266 a.u which is in accordance with that in the appendix[1]. The low energy of this conformer can be attributed to the attractive overlap of a pi orbital with a vinyl proton[2]. There is also little steric hindrance in this form which also contributes to its relative stability.
Ci anti2 conformation of 1,5-hexadiene
Initial optimisation
The molecule was then drawm in the anti2 structure as shown in the appendix. The calculation was carried out using the same method as the previous ones. The details of the calculation are shown below:
File Name = ANTI PART 2 File Type = .log Calculation Type = FOPT Basis Set = 3-21G Calculation Method = RHF Charge = 0 Spin = Singlet E(RHF) = -231.69253526 a.u. RMS Gradient Norm = 0.00001131 a.u. Imaginary Freq = Dipole Moment = 0.0003 Debye Point Group = C1 Job cpu time: 0 days 0 hours 0 minutes 55.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000036 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.001277 0.001800 YES
RMS Displacement 0.000555 0.001200 YES
Predicted change in Energy=-2.533308D-08
Optimization completed.
-- Stationary point found.
The molecule was symmetrized and the point group was assigned Ci. The energy of this molecule is given as -231.69254 a.u which is exactly the same as given in the appendix[1].
Using a higher basis set
The molecule was then optimized using a higher basis set of B3LYP/6-31G*(d) and the method was changed to DFT. Using a higher basis set should improve the accuracy of the calculation as it takes into account more orbitals.
File Name = ANTI PART 2 3ND OPT File Type = .log Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -234.61171035 a.u. RMS Gradient Norm = 0.00001368 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = C1 Job cpu time: 0 days 0 hours 4 minutes 52.4 seconds
Item Value Threshold Converged?
Maximum Force 0.000016 0.000450 YES
RMS Force 0.000007 0.000300 YES
Maximum Displacement 0.000262 0.001800 YES
RMS Displacement 0.000089 0.001200 YES
Predicted change in Energy=-1.684326D-08
Optimization completed.
-- Stationary point found.
The optimal energy of this molecule was calculated as 234.61171 a.u. This is a difference in energy from the lower basis set of (234.61171-231.69254) 2.91917 a.u which is equal to 1831.81 kcal/mol. This is a large difference in energy and shows that using a more accurate basis set gives a vastly different result. When symmetrized the point group of the molecule remained the same as expected.
Frequency analysis
A frequency calculation was then carried out in order to ensure a minimum was formed. A summary of the calculation is shown below:
File Name = anti part2 freq File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -234.61171035 a.u. RMS Gradient Norm = 0.00001356 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = CI Job cpu time: 0 days 0 hours 3 minutes 33.6 seconds.
As the vibration low frequencies are positive it is shown that a minimum structure has formed.
Low frequencies --- -9.5023 0.0003 0.0004 0.0007 3.6742 12.9712
Low frequencies --- 74.2843 80.9985 121.4135
Item Value Threshold Converged?
Maximum Force 0.000036 0.000450 YES
RMS Force 0.000014 0.000300 YES
Maximum Displacement 0.000299 0.001800 YES
RMS Displacement 0.000122 0.001200 YES
Predicted change in Energy=-1.567477D-08
Optimization completed.
-- Stationary point found.
Thermochemistry
From the output file it was possible to find the following energy data:
Sum of electronic and zero-point Energies= -234.469203 Sum of electronic and thermal Energies= -234.461857 Sum of electronic and thermal Enthalpies= -234.460913 Sum of electronic and thermal Free Energies= -234.500777
Optimizing the chair and boat conformations
Chair conformation
Initial optimization
Initially an allyl fragment was optimized using a HF/3-21G level of theory. This was carried out as it is possible to use these fragments in order to create the chair and boat transition structures. A summary of the calculation is shown below:
File Name = allyl optimisation File Type = .log Calculation Type = FOPT Calculation Method = UHF Basis Set = 3-21G Charge = 0 Spin = Doublet E(UHF) = -115.82304010 a.u. RMS Gradient Norm = 0.00003049 a.u. Imaginary Freq = Dipole Moment = 0.0292 Debye Point Group = C1 Job cpu time: 0 days 0 hours 0 minutes 14.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000048 0.000450 YES
RMS Force 0.000018 0.000300 YES
Maximum Displacement 0.000146 0.001800 YES
RMS Displacement 0.000070 0.001200 YES
Predicted change in Energy=-1.277268D-08
Optimization completed.
-- Stationary point found.
Finding the chair transition state
Once the allyl molecule was optimized it was possible to model a chair conformation by arranging two of the molecules in the shape of the chair conformer and changing the distance between the terminal carbons to 2.2A. A calculation was then run, the job type was changed to Opt+freq and the optimization tab was changed from Optimization to a Minimum to Optimization to a TS (Berny). A summary of the calculation is shown below:
File Name = CHAIR OPT GUESS REAL File Type = .log Calculation Type = FREQ Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.61932234 a.u. RMS Gradient Norm = 0.00004804 a.u. Imaginary Freq = 1 Dipole Moment = 0.0005 Debye Point Group = C1 Job cpu time: 0 days 0 hours 0 minutes 19.0 seconds.
D-Space Chair transition state
Low frequencies --- -818.0084 -2.9241 0.0006 0.0009 0.0009 6.1634
Low frequencies --- 6.7932 209.6755 395.9958
Item Value Threshold Converged?
Maximum Force 0.000086 0.000450 YES
RMS Force 0.000015 0.000300 YES
Maximum Displacement 0.001145 0.001800 YES
RMS Displacement 0.000217 0.001200 YES
Predicted change in Energy=-1.402891D-07
Optimization completed.
-- Stationary point found
As can be seen from the low frequencies data above, there is one negative frequency at -818.0084cm-1, this shows that a transition state has been reached. Below is an animation of the molecule at this frequency. As you can see the two terminal carbons on the two allyl groups are moving alternatively towards and then away from one another. This corresponds to the cope rearrangement discussed earlier.
Frozen co-ordinates
The transition state was then optimized using a frozen co-ordinates method. A similar method was used as previously, except this time the terminal carbon bond distance was locked at 2.20A using the redundant coordinate editor. The calculation was set to optimised to a minimum. Details of the calculation are show below:
File Name = CHAIR FROZEN CORD File Type = .log Calculation Type = FOPT Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.61517913 a.u. RMS Gradient Norm = 0.00325829 a.u. Imaginary Freq = Dipole Moment = 0.0001 Debye Point Group = C1 Job cpu time: 0 days 0 hours 0 minutes 33.0 seconds.
Item Value Threshold Converged?
Maximum Force 0.000050 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000935 0.001800 YES
RMS Displacement 0.000167 0.001200 YES
Predicted change in Energy=-2.653157D-07
Optimization completed.
-- Stationary point found.
Chair frozen co-ordinates D-space
Further optimization of terminal bonds
The chair transition state was then further optimized by altering the terminal C-C bonds. In this calculation, instead of freezing the bond length the calculation was set to derivative. This enables us to optimize the length of the C-C bonds instead of locking them at 2.2A. Details of the calculation are shown below:
File Name = chair frozene dd File Type = .log Calculation Type = FTS Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.61932198 a.u. RMS Gradient Norm = 0.00005629 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = C1 Job cpu time: 0 days 0 hours 1 minutes 48.9 seconds.
Item Value Threshold Converged?
Maximum Force 0.000026 0.000450 YES
RMS Force 0.000008 0.000300 YES
Maximum Displacement 0.000906 0.001800 YES
RMS Displacement 0.000177 0.001200 YES
Predicted change in Energy=-2.922277D-07
Optimization completed.
-- Stationary point found.
This energy value of-231.61932 a.u is in good accordance with the appendix[1].
Boat conformation
In order to estimate the boat conformation, the optimised anti-peri planar molecule was used. It was necessary to manually label the atoms to ensure that the correct rearrangement took place. An OPT+FREQ calculation was then run, optimizing to a QST2 transition state. The details of the calculation are shown below:
File Name = boat opt 1 File Type = .log Calculation Type = FREQ Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.61932221 a.u. RMS Gradient Norm = 0.00004810 a.u. Imaginary Freq = 1 Dipole Moment = 0.0000 Debye Point Group = C2H Job cpu time: 0 days 0 hours 0 minutes 11.8 seconds.
Initial boat calculation D-space
Item Value Threshold Converged?
Maximum Force 0.000036 0.000450 YES
RMS Force 0.000018 0.000300 YES
Maximum Displacement 0.000750 0.001800 YES
RMS Displacement 0.000286 0.001200 YES
Predicted change in Energy=-2.657648D-07
Optimization completed.
-- Stationary point found.
As you can see from the diagram below the calculation was unable to find the boat transition state. This is because Gaussian is unable to rotate the bonds so this must be done manually.
The calculation was re-run, setting the dihedral angle between the four inner carbons to 00 and C2-C3-C4 and C3-C4-C5 to 900. A summary of of the calculation is shown below:
File Name = boat opt 2 File Type = .log Calculation Type = FREQ Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.60280239 a.u. RMS Gradient Norm = 0.00003238 a.u. Imaginary Freq = 1 Dipole Moment = 0.1584 Debye Point Group = CS Job cpu time: 0 days 0 hours 0 minutes 15.3 seconds.
Item Value Threshold Converged?
Maximum Force 0.000105 0.000450 YES
RMS Force 0.000022 0.000300 YES
Maximum Displacement 0.001248 0.001800 YES
RMS Displacement 0.000277 0.001200 YES
Predicted change in Energy=-9.839029D-08
Optimization completed.
-- Stationary point found.
Second boat optimisation D-space
As there is one negative frequency a transition structure has been reached. Below is an animation of the negative frequency at at -839.93cm-1. This animation shows a cope rearrangement in the boat transition state.
Low frequencies --- -839.9283 -8.0758 -6.3115 -4.0797 -0.0006 -0.0006 Low frequencies --- 0.0004 155.0909 382.2138 ****** 1 imaginary frequencies (negative Signs) ******
The energy value of -231.60280 a.u is in accordance with the appendix[1].
IRC calculation
In order to predict which conformers the chair and boat transition states connect it is necessary to run an intrinsic reaction co-ordinate calculation. . This method allows Gaussian to follow a minimum energy pathway from the transition state to a minimum on the potential energy surface. It does this by taking small geometric steps in order to create points where the gradient of the PES is the steepest. This calculation was run on the optimized chair transition state. Details of the calculation are shown below:
File Name = chair IRC File Type = .log Calculation Type = IRC Calculation Method = Basis Set = Charge = 0 Spin = Singlet E(RHF) = -231.69157881 a.u. RMS Gradient Norm = 0.00015224 a.u. Imaginary Freq = Dipole Moment = 0.3631 Debye Point Group = C1 Job cpu time: 0 days 0 hours 10 minutes 46.4 seconds.
This reaction was set to take a maximum of 50 steps, however it managed to find a solution in 44. Below is a table showing the reaction co-ordinate diagram and an animation of this. The animation shows the reactant forming from the transition state as explained above.
| IRC | Animation |
|---|---|
 |

|
The optimized energy of the last structure is -231.69158 a.u which means it the gauche 4 conformer.
IRC optimisation
As the IRC calculation doesn't reach a minimum a further calculation need to be carried out. One method of doing this is optimizing the final structure from the IRC. This calculation was run under a 6-31g* basis set and the details of this calculation are shown below:
File Name = Chair optimisation
File Type = .log
Calculation Type = FOPT
Calculation Method = RHF
Basis Set = 3-21G
Charge = 0
Spin = Singlet
E(RHF) = -231.69166702 a.u.
RMS Gradient Norm = 0.00000475 a.u.
Imaginary Freq =
Dipole Moment = 0.3806 Debye
Point Group = C2
Job cpu time: 0 days 0 hours 0 minutes 28.9 seconds.
Item Value Threshold Converged?
Maximum Force 0.000010 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000298 0.001800 YES
RMS Displacement 0.000091 0.001200 YES
Predicted change in Energy=-2.406992D-09
Optimization completed.
-- Stationary point found.
This calculation gave a minimum energy of -231.69167 a.u. Another, potentially more accurate method of finding a minimum energy is by increasing the number of steps that Gaussian can take in the IRC calculation. This calculation was carried out and the maximum number of steps was increased from 50 to 100. However, when this calculation was run, it still only took 44 steps and gave exactly the same result. I therefore chose not to include this calculation in this wiki page.
Further optimisation of chair and boat transition states
Chair
The chair transition state was then further optimized at a B3LYP/6-31G* level of theory. A frequency analysis was then carried out. Details of the frequency calculation on the optimized structure are shown below:
File Name = chair 6-31g freq File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -234.55698262 a.u. RMS Gradient Norm = 0.00005024 a.u. Imaginary Freq = 1 Dipole Moment = 0.0001 Debye Point Group = C1 Job cpu time: 0 days 0 hours 5 minutes 15.2 seconds.
Boat
The same calculations were carried out on the boat transition state. Details of the calculation are shown below:
File Name = boat 6-31g freq File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -234.54307852 a.u. RMS Gradient Norm = 0.00003878 a.u. Imaginary Freq = 1 Dipole Moment = 0.0612 Debye Point Group = CS Job cpu time: 0 days 0 hours 3 minutes 50.6 seconds.
Energy of chair TS: -234.55698 a.u.
Energy of boat TS: -234.54308 a.u.
As you can see from these values, the chair transition structure is lower in energy then the boat transition structure.
Comparison with the lower basis set
Below is a table showing the difference in energies between the HF/3-21G and the B3LYP/6-31G* basis sets for the chair and boat transition states.
| Transition State | Optimized energy at HF/3-21G basis set (a.u) | Optimized energy at B3LYP/6-31G* basis set (a.u) |
|---|---|---|
| Chair | -231.61932 | -234.55698 |
| Boat | -231.60280 | -234.54308 |
As can be seen from the results above there is a reasonably large difference in energy between the two basis sets. The B3LYP/6-31G* basis set is more accurate and gives results more similar to experimental results.
Comparison of thermochemistry data
The following thermochemistry data was taken from the frequency analysis of the chair and boat structures respectively:
Chair
Zero-point correction= 0.142051 (Hartree/Particle) Thermal correction to Energy= 0.147973 Thermal correction to Enthalpy= 0.148917 Thermal correction to Gibbs Free Energy= 0.113165 Sum of electronic and zero-point Energies= -234.414932 Sum of electronic and thermal Energies= -234.409010 Sum of electronic and thermal Enthalpies= -234.408066 Sum of electronic and thermal Free Energies= -234.443818
Boat
Zero-point correction= 0.140739 (Hartree/Particle) Thermal correction to Energy= 0.147086 Thermal correction to Enthalpy= 0.148030 Thermal correction to Gibbs Free Energy= 0.111310 Sum of electronic and zero-point Energies= -234.402340 Sum of electronic and thermal Energies= -234.395993 Sum of electronic and thermal Enthalpies= -234.395049 Sum of electronic and thermal Free Energies= -234.431768
Using this thermochemistry data it is possible to calculate the activation energy for this reaction at 298K and 0K. To calculate the activation at 298K it is necessary to find the difference between the sum of the electronic and thermal energies of the transition state and the reactant. In this case the reactant is the Anti2 conformer and the thermochemistry data was stated previously. When finding the activation at 0K it is neccessary to find the difference between the zero point energies of the transition state and the reaction. An example of the calculation is shown below:
Activation energy of chair TS at 298K: (-234.409010+234.461857)= 0.052847 a.u =33.162 kcal/mol
A table summarizing the other activation is shown below:
| Transition State | Activation Energy at 0 K (3 dp)(kcal/mol) | Activation Energy at 298 K (3 dp) (kcal/mol) |
|---|---|---|
| Chair | 34.055 | 33.162 |
| Boat | 41.957 | 41.330 |
These values are in accordance with the data in the appendix. As expected the activation energies for the chair transition states are lower then that of the boat transition state. This is most likely because the increased steric hindrance in the boat transition state due to the fragments being adjacent to one another and facing the same way. In the chair transition state the fragments are rotated opposite one another and hence have less steric hindrance.
The Diels Alder Cycloaddition
Introduction
The [4+2] Diels Alder cycloaddition is a common method of synthesizing cyclic compounds from an alkene and compounds containing a cis-diene. The general mechanism for these reactions is shown below:
These reactions can be stabalised by adding electron withdrawing groups such as carbonyl groups to the alkene fragment (dienophile). This lowers the energy of the LUMO of the dienophile, meaning that is can more readily react with the HOMO of the diene. The selectivity of these reactions is dominated by kinetics and the endo isomer generally dominates.
Simple Diels Alder reaction
Optimizing Cis-butadiene
Initially cis-butadine was optimised using the M1 semi empirical molecular orbital method. The details of the calculation are shown below:
File Name = initial cis butadiene optimisation File Type = .log Calculation Type = FOPT Calculation Method = RAM1 Basis Set = ZDO Charge = 0 Spin = Singlet E(RAM1) = 0.04879734 a.u. RMS Gradient Norm = 0.00008900 a.u. Imaginary Freq = Dipole Moment = 0.0414 Debye Point Group = C1 Job cpu time: 0 days 0 hours 0 minutes 11.1 seconds.
Item Value Threshold Converged?
Maximum Force 0.000159 0.000450 YES
RMS Force 0.000051 0.000300 YES
Maximum Displacement 0.000661 0.001800 YES
RMS Displacement 0.000254 0.001200 YES
Predicted change in Energy=-1.540760D-07
Optimization completed.
-- Stationary point found.
By looking at the HOMO and LUMO of the molecule, it is possible to determine whether these two orbitals are symmetric or anti-symmetric.
| HOMO | LUMO |
|---|---|
 |

|
As the diagram shows, the HOMO is anti-symmeteric with a nodal plane and the LUMO is symmetric around a plane in the centre.
Ethene optimization
A molecule of ethene was optimized using the same method. Details of the calculation are shown below:
File Name = ETHENE OPTIMSIATION File Type = .log Calculation Type = FOPT Calculation Method = RAM1 Basis Set = ZDO Charge = 0 Spin = Singlet E(RAM1) = 0.02619024 a.u. RMS Gradient Norm = 0.00000945 a.u. Imaginary Freq = Dipole Moment = 0.0000 Debye Point Group = C1 Job cpu time: 0 days 0 hours 0 minutes 3.0 seconds.
The HOMO and LUMO of the optimized molecule ethene molecule are shown below:
| HOMO | LUMO |
|---|---|
 |

|
From these diagrams you can see that the HOMO is symmetric and the LUMO is anti-symmetric. You can see that these symmetries are opposite to those of the HOMO and LUMO of cis-butadiene. This is an important observation as it means the two molecules adhere to the Woodward-Hoffman rules. The Diels Alder reaction is a [4n+2] cycloaddition reaction and reacts under thermal condition. It therefore goes through a Huckel transition state. In order for this reaction to follow the Woodward-Hoffman rules, the HOMO of the dienophile must have the same symmetry to the LUMO of the diene and the LUMO of the dienophile must have the same symmetry to the HOMO of the diene. As both of these are true in this case the reaction may proceed.
Finding the transition state
The transition state of the Diels Alder reaction was investigated by using the optimised molecules of cis-butadiene and ethene. The two molecules were arranged in position to imitate an envelope structure. This structure allows maximum overlap between the HOMO of cis-butadiene and the LUMO of the ethene molecule which is crucial for a Diels alder reaction to take place. The distance between the terminal carbons atoms was initially frozen to 2.2A as done previously in the frozen co-ordinate calculation and then optimistized using the Heisman derivative method using the 6-31g basis set. The details of the final calculation are shown below:
File Name = DA TS higher basis set derivative File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -234.54389638 a.u. RMS Gradient Norm = 0.00005586 a.u. Imaginary Freq = 1 Dipole Moment = 0.3944 Debye Point Group = C1 Job cpu time: 0 days 0 hours 5 minutes 6.0 seconds.
As there is one imaginary frequencies (-524.65cm-1) we know the transition state has been found.
Low frequencies --- -524.6525 -0.0004 0.0002 0.0003 1.2635 10.8025
Low frequencies --- 19.5848 135.4750 203.7379
Item Value Threshold Converged?
Maximum Force 0.000210 0.000450 YES
RMS Force 0.000034 0.000300 YES
Maximum Displacement 0.001493 0.001800 YES
RMS Displacement 0.000436 0.001200 YES
Predicted change in Energy=-1.777204D-07
Optimization completed.
-- Stationary point found.
| HOMO | LUMO |
|---|---|
 |

|
As can be seen from the diagrams above, the HOMO is anti-symmetric with respect to the plane whereas the LUMO is symmetric with respect to the plane. By looking at the shape of the HOMO and knowing that its anti-symmetric, you can deduce that it is formed from the anti-symmetric orbitals of ethene and cis-butadiene which are the LUMO and HOMO respectively. The same logic can be applied to LUMO, it is therefore formed by the HOMO of ethene and the LUMO of cis-butadiene.
By looking at the results of the calculation, is it possible to find the bond distance between the terminal carbon atoms in the ethene and cis-butadiene molecules in the Diel Alder transition state.
GaussView shows that this bond distance is 2.27A. If you compare this with the standard sp2 and sp3 C-C bond distances which are 1.46A and 1.53A respectively it is a longer and hence weaker. However, as the standard van der Vaal radius of a carbon atom is 1.7A[3], if the two atoms had no interactions you would expect the two carbon atoms to be at least 3.4A apart. Therefor this shows that there is some favorable interactions between the carbon atoms in the transition state.
If you look at the imaginary vibration shown below, you can see that it shows the two new C-C bonds forming in a concerted, synchronized manner.
Below is an animation showing the lowest positive vibration (135.40cm-1) of the Diel Alder transition state:
If you compare this vibration to the one above you can see that this is a non-bond forming vibration as the two fragments are not moving towards one another.
Investigating endo and exo transition states
In this section, I will investigate the endo and exo transition states in the Diels Alder reaction between maelic anhydride and cyclohexadiene.
Endo transition state
In order to investigate the endo transition state I initially optimized the maelic anydride and cycloheaxdiene molecules and then constructed an envelope style transition state with these optimized fragments as done previously. I then used the same method as previously to optimize to a transition state. The details of the final calculation are shown below:
File Name = endo TS File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -612.68339678 a.u. RMS Gradient Norm = 0.00000895 a.u. Imaginary Freq = 1 Dipole Moment = 6.1146 Debye Point Group = C1 Job cpu time: 0 days 0 hours 24 minutes 47.1 seconds
As there is one imaginary (negative) frequency it shows that the transition state has been reached.
Low frequencies --- -447.1329 -14.3190 -0.0004 -0.0002 0.0006 4.4124 Low frequencies --- 11.3354 59.6398 118.3342 ****** 1 imaginary frequencies (negative Signs) ******
Below is a diagram showing the endo transition state:
Exo transition state
A similar method was used to find the exo transition state. Details of the calculation are shown below:
File Name = exo ts with freq File Type = .log Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -612.67931096 a.u. RMS Gradient Norm = 0.00000682 a.u. Imaginary Freq = 1 Dipole Moment = 5.5502 Debye Point Group = C1 Job cpu time: 0 days 0 hours 25 minutes 5.5 seconds
Again only one negative frequency has been calculated so the transition state has been reached.
Low frequencies --- -448.5315 -13.8989 -11.7827 0.0007 0.0009 0.0009 Low frequencies --- 3.2024 53.3162 109.0983 ****** 1 imaginary frequencies (negative Signs) ******
Below is an image of the exo transition state:
Comparison of energy
Below is a table showing the difference in energy between the two transition states:
| Transition state | Energy (A.U) | Energy (kcal/mol) |
|---|---|---|
| Endo | -612.68340 | -384464.96 |
| Exo | -612.67931 | 384462.38 |
As the table shows the endo transition state has a lower energy by around 2.5kcal/mol. This difference in energy is attributed to the difference in structure between the two transition states. In the endp TS the new C=C bond is formed directly above the anhydride group. Whereas in the exo form the C=C is formed away from the anhydride group. In the endo TS the pi orbitals of the carbonyl groups can form positive interactions with the pi orbitals in the alkene group as they are close together. This stabilizes the transition state, causing it to be lower in energy and making the reaction more kinetically stable. This effect is known as secondary orbital overlap as it involves orbitals which are not the frontier bonding orbitals. This effect can not take place in the exo TS which is why it is higher in energy. The exo product is however thermodynamically more stable so if the reaction was carried out at a high temperature then this product would be favored.
| EXO | ENDO | |
|---|---|---|
 |

|
Conclusion
During this project it was discovered that in the Cope Rearrangement the chair transition state is lower in energy then the boat transition state and therefore the activation energy is lower for the chair transition state and is kinetically favored. In the second part of the project the Diels Alder reaction was investigated. It was shown endo selectivity is favored even though the exo product is more thermodynamically stable. This is because the reaction is mostly governed by kinetics and the endo transition state has a lower energy then the exo which is mostly related to the secondary orbital interactions.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 M.Bearpark., (2012)., Moecule 3, Physical (Computational Lab)., [Lab Script]., Imperial College London., Autumn 2012., Appendix
- ↑ B W. Gung, Z Zhu, R A. Fouch., ,J. Am. Chem. SOC. 1995,117, 1783-1788[Diene Conformers]., Imperial College London., Autumn 2012., Diene Conformations
- ↑ A. Bondi. J. Phys. Chem., 1964, 68 (3) pp 441-451., DOI:10.1021/j100785a001