Module 3

Introduction

The aim of this module is to develop the computational quantum mechanics based methods used in Module 2 to analyse transition states and the lowest energy reaction pathways for the Cope rearrangement and then for a number of Diels Alder reactions.

The Cope Rearrangement

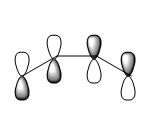
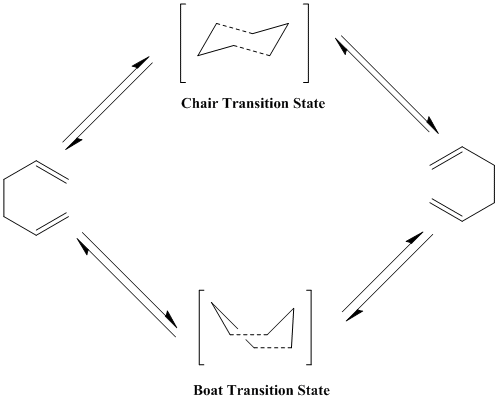
The Cope Rearrangement is a specific [3,3]-sigmatropic shift rearrangement of a 1,5-diene resulting in a regioisomeric 1,5-diene.(Org pp947) The rearrangement of 1,5-hexadiene proceeds thermally in a concerted pericyclic fashion via either a "chair" or "boat" Hückel transition state.^[1]

In this section the reactant and product energy minima are first determined using the optimisation methods of Gaussview, using the relatively crude method of HF/3-21G. The apparent lowest energy conformers are then further optimised using the higher-level theory of the B3LYP/6-311G(d) method. The transition state structure and energy minima is then determined using this method as well as the activation energy and IRC calculation to determine the reaction coordinates of the reaction.

Optimising the Reactants and Products

The conformers of 1,5-hexadiene were drawn and optimised first using Gaussview, set to HF/3-21G. This allowed comparison of the conformers to determine those lowest in energy. The conformers were classed into two groups; Anti, where the two propene groups are antiperiplanar to each other and Gauche, where the two propene groups are synperiplanar to one another. These two broad categories are subdivided into conformers with more subtle differences between their structures. Ten of these structures were modelled and the Symmetries function used to determine their point group symmetry; see below table.


Conformer	Point Group	Energy (hartree)	Relative Energy kcalmol^-1	Link to D space^-1
Anti 1	C₂	-231.69260	0.04	?
Anti 2	C_i	-231.69254	0.08	?
Anti 3	C_2h	-231.68907	2.25	?
Anti 4	C₁	-231.69097	1.06	?
Gauche 1	C₁	-231.68771	3.11	?
Gauche 2	C₂	-231.69167	0.62	?
Gauche 3	C₁	-231.69266	0	?
Gauche 4	C₂	-231.69153	0.71	?
Gauche 5	C₁	-231.68962	1.91	?
Gauche 6	C₁	-231.68916	2.20	?

The lowest energy conformer using HF/3-21G is was demonstrated to be Gauche 3, with an energy of -231.269266a.u. ; 0.04kcalmol^-1 lower than the nearest conformer, Anti 1. The Anti 2 conformer was of similar low energy and hence these three conformers were chosen to be investigated further using the more rigorous DFT B3LYP/6-31G* optimisation method.

Using the higher-level theory of DFT B3LYP/6-31G*


Conformer	Energy (hartree)	Relative Energy kcalmol^-1	Link to D space^-1
Anti 1	-234.6118	0.00	????
Anti 2	-234.6117	0.06	????
Gauche 3	-234.6113	0.31	???

Contrary to the preliminary optimisation using HF/3-21G, it was found that after optimisation using DFT B3LYP/6-31G* the results indicate that the lowest energy conformer is Anti 1, with point group C₂. Since a higher-level and more detailed theoretical method is used to compute this result, it is the more accurate result and is easily explained by theory. The structure of Anti conformations are highly favourable since the two alkene groups point in the same direction, but as far apart from each other as possible. The molecule is in the right geometry for sigma hyperconjugation between the C-H and C-C sigma bonds and the C-C and C-H antibonding orbitals. The Gauche conformations are higher in energy since the hyperconjugation is not present to nearly the same extent, and hence the stabilising effect is lost. There is also more steric hindrance present in more Gauche conformations than in the anti conformations of the molecule since bulkier groups are closer together. The bond angle of 116^o in Gauche 1, for example is much less favourable than that of 111^o found in the Anti 1 molecule; hence greater strain.

The energies were first analysed using the HF/3-21G method.

Using HF/3-21G - at 298K , 1 atm


Conformer	Sum of electronic & zero-point energy (Hartree)	Sum of electronic & thermal energies (Hartree)	Sum of electronic & thermal enthalpies (Hartree)	Sum of electronic & thermal-free energies (Hartree)	Link to D space^-1
Anti 1	-231.5396	-231.5326	-231.5317	-231.5703	????
Anti 2	-231.5395	-231.5326	-231.5316	-231.5709	????
Gauche 3	-231.5395	-231.5326	-231.5317	-231.5706	???

The energies were then analysed using the DFT B3LYP/6-31G* method.

Using DFT B3LYP/6-31G* - at 298K , 1 atm


Conformer	Sum of electronic & zero-point energy (Hartree)	Sum of electronic & thermal energies (Hartree)	Sum of electronic & thermal enthalpies (Hartree)	Sum of electronic & thermal-free energies (Hartree)	Link to D space^-1
Anti 1	-234.469285	-234.461964	-234.461020	-234.500163	????
Anti 2	-234.469181	-234.461849	-234.460905	-234.500697	????
Gauche 3	-234.468692	-234.461459	-234.460515	-234.500115	???

Vibrational Analysis

Frequency analysis using GaussView with the same method of DFT B3LYP/6-31G*, was performed so as to confirm that the structures which were obtained during the optimisation were at ground state, rather than transition states, and hence that products were formed. Vibrational analysis calculates the second derivative of the potential energy surface, allowing it to be determined whether the optimisation produced minima, transition states of maxima The C=C vibrations were investigated and displayed in the table below as an example. (Double-click to see animation of vibration)


Conformer	Frequency 1 /cm^-1	Intensity	Frequency 2 /cm^-1	Intensity
Anti 1	1731.5	4.7	1734.5	13.5
Anti 2	1731.4	0	1734.7	18.2
Gauche 3	1732.0	6.9	1733.0	6.1

Since the low frequency values obtained for 1,5-hexadiene were all positive, all of the vibrations were real rather than imaginary, confirming that the reaction occurred to completion and the products were formed.

Optimising the "Chair" and "Boat" Transition Structures

Since it is a rearrangement, the optimisation 1,5-hexadiene resulted in the lowest energy conformation of the reactants and products to be found. The transition state, which can either be a boat or chair, are then optimised to determine their structure and energy minima.

Chair

TS (Berny) Guess Optimisation

The structure of the chair transition state was drawn approximately, with equivalent terminal carbons positioned 2.2Å apart.

Frozen Coordinate Optimisation

The equivalent terminal carbon atoms were 'frozen' at a distance of 2.2Å from each other and the molecule optimised using HF/3-21G. These atoms were then unfrozen and the molecule optimised once more to give the final structure.


Method:	Optimised Guess	Frozen Coordinates	Unfrozen Coordinates
Structure
Terminal C-C bond length (Å)	2.02	2.20	2.02
Imaginary Frequency (cm^-1)	-817.9	-765.0	-818.0
Total Energy (hartree)	-231.619	-231.615	-231.619

The imaginary vibration for the Optimised guess Chair transition state is shown below.

Boat

The original optimisation failed due to the approximate transition state being too rough an approximation. Instead of a boat conformation, a chair conformation is formed.

Instead, the initial starting reactant and product were drawn and used to obtain the transition state.


Reactant	Product

The energy for the boat transition state calculated was found to be lower than that of the chair transition state, as expected, since this is stated in literature.^[2]


Transition State	Illustration	Energy (hartrees)	Sum of electronic & zero-point energy (Hartree)	Sum of electronic & thermal energies (Hartree)	Sum of electronic & thermal enthalpies (Hartree)	Sum of electronic & thermal-free energies (Hartree)	Link to D space^-1
Boat TS (HF/3-21G)		-231.603	-231.451	-231.445	-231.444	-231.480	????
Boat TS (DFT B3LYP/6-31G*)		-234.543	-234.4023	-234.3960	-234.3951	-234.4318	????

IRC

The correct transition state of the Cope rearrangement cannot be predicted by observation alone. Instead, the Intrinsic Reaction Coordinated method is used which calculates where the potential energy gradient is steepest and hence finds the energy minimum and more probable transition state structure.

The chair transition state which had been optimised using the frozen coordinate method was used to perform IRC on. Using 50 steps and the forward reaction setting, an IRC was performed since the reaction coordinate for the Cope re-arrangement is symmetrical. However, the calculation did not reach a minimum geometry.

Instead the settings were changed to 'calculate force constant of each step', which allowed the method to continually reevaluate the calculation, resulting in a minima being found.

Activation Energy

Using DFT B3LYP/6-31G*


Transition State	Energy (hartree)	Activation Energy kcalmol^-1	Literature Activation Energy kcalmol^-1	Link to D space^-1
Chair TS	-234.550	38.78	33.5 ± 0.5	????
Boat TS	-234.437	109.69	44.7 ± 2.0	????

The activation energy was found by comparing the energy of the transition state with that of the lowest energy, Anti 1, conformer.

The Diels Alder Cycloaddition

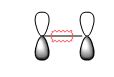
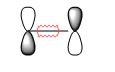
The Diels Alder reaction is a pericyclic reaction between a diene and a dienophile in which the π-orbitals of the dienophile are used to form two new σ bonds through interaction with the π orbitals of the diene. The number π-electron is six (4n+2) and so the reaction proceeds thermally by a concerted suprafacial Hückel transition state.

Ethylene and Butadiene

Diels-Alder reaction of butadiene and ethylene has only one possible transition state due to the very high level of symmetry of the ethene molecule.


Molecular Orbital	Symmetry	Link to D space^-1
Butadiene LUMO	Symmetric	????
Butadiene HOMO	Asymmetric	????
Ethene LUMO	Asymmetric	????
Ethene HOMO	Symmetric	????


Transition State MO	MO from Computational Methods	MO from LCAO Theory	Symmetry	Link to D space^-1
TS LUMO			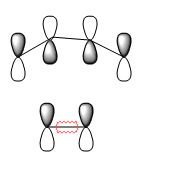Symmetric	????
TS HOMO			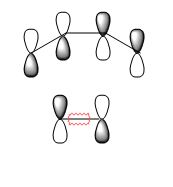Asymmetric	????

Reaction between Cyclohexa-1,3-diene and Maleic Anhydride

This is a regioselective Diels-Alder reaction since there are two possible reaction mechanisms; via the endo intermediate or via the exo intermediate. Since both reactants contain substituent groups, secondary orbital interactions occur.


Molecular Orbital	MO from Computational Methods	Link to D space^-1
Cyclohexadiene LUMO		????
Cyclohexadiene HOMO		????
Maleic Anhydride LUMO		????
Maleic Anhydride HOMO		????


Transition State MO	MO from Computational Methods	MO from LCAO Theory	Symmetry	Link to D space^-1
TS LUMO	File:?	File:?	Symmetric	????
TS HOMO	File:?	File:?	Symmetric	????

The GaussView optimisation of both the Endo and Exo products continually failed, and unfortunately due to time constraints, it was not possible to produce the final HOMO and LUMO MOs for the Endo and Exo transition states and products.

However from theory it is know that although there is more steric hinderance in the endo transition state, the greater secondary orbital overlap results in it being the more stable transition state.^[3]

Conclusion

Computational methods are successful in analysing molecules and transition states to a high degree of accuracy. From this, activation energies and hence the lowest energy pathway for a reaction can be determined.

References

↑ O. Wiest, K. A. Black, K. N. Houk, J. Am. Chem. Soc., 1994, 116, 10337
↑ Module 3 Instruction Sheet
↑ Clayden, J., Greeves, N., Warren, S. & Wothers, P. Organic Chemistry, 2005, pp916

[1] O. Wiest, K. A. Black, K. N. Houk, J. Am. Chem. Soc., 1994, 116, 10337

[2] Module 3 Instruction Sheet

[3] Clayden, J., Greeves, N., Warren, S. & Wothers, P. Organic Chemistry, 2005, pp916

[1]

[2]

[3]