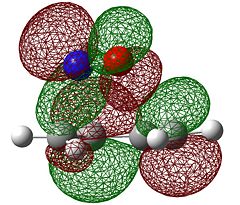
Rep:Mod:3qpzm1029

Module 3: The Transition State

The aim of this experiment will be to study the transition state structures for two different classes of pericyclic reactions. The first will be the Cope Rearreangement, a well-studied [3,3] sigmatropic shift of 1,5-hexadiene, and the second will be the Diels-Alder reaction between 1,3-cyclohexadiene and maleic anhydride, a [4+2] cycloaddition.

Unlike module 1, where it worked well, molecular mechanics cannot be used here for it can only describe bonds which are fully formed. For these experiments, the transition state structures will be calculated using molecular orbital based methods which solve the Schrodinger equation and hence locate maxima in the resulting potential energy surface.

The Cope Rearrangement

Optimisation of 1,5 hexadiene Conformers

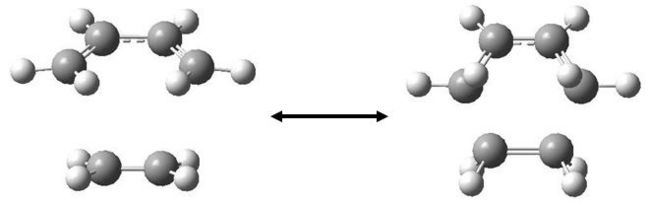
The reaction is scheme of the Cope Rearrangement is as follows:

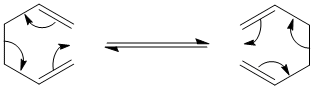
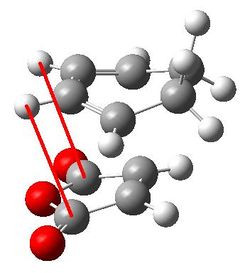
The 1,5 hexadiene molecule which undergoes this intramolecular process can exist as magnitude of conformers. Some of these conformers were modelled using the Hartree-Fock method and 3-21G basis set (HF/3-21G). The first obvious choice was between a gauche and anti linkage between the two sp³ carbons. Below, is the result of an optimisation for a gauche conformer.

The designation of the optimised structure in the course wiki are shown in brackets.

-231.68771617 Hartree with C₂ symmetry (gauche1)

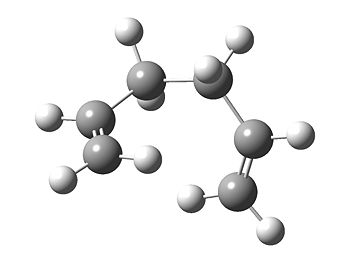
It was found that this conformer has C₂ symmetry.

In an attempt to see if a lower energy conformer exists, the C-C bonds were twisted around (to put the two sp² carbons as far apart as possible) and the same calculation was run again.

-231.69153035 Hartree with C₂ symmetry (gauche2)

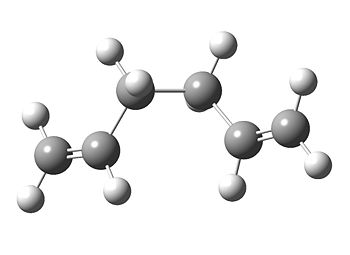
Once again, we have found a C₂ conformer, but this time the energy is lower, as expected. In order to find an even lower energy conformer, the next logical step was to find a molecule with lower, C₁ symmetry as gaussview never breaks symmetry (unless specifically instructed to). A lower symmetry molecule gives the molecule more flexibility so that the calculation can optimise to a lower energy.

-231.69266122 Hartree with C₁ symmetry (gauche3)

We have found a (C₁) conformer which is indeed the lowest in energy, demonstrating the implication of point group symmetry on gaussian optimisations.

Next, the exact same method and basis set (HF/3-21G) were used to optimise a 1,5 hexadiene molecule with anti linkage, which we would expect to be of lower energy than gauche due to lessened steric repulsion between the vinyl groups which are now further away from each other (180 degrees dihedral angle as opposed to 60 degrees).

-231.69253506 Hartree with C_i symmetry (anti2)

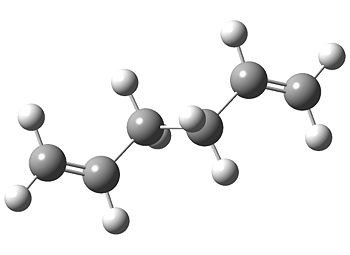
We have found a C_i conformer with a point of inversion. This species is lower than energy than the previous gauche C₂ molecules but not the C₁. We will now optimise an anti C₁ conformer.

-231.69097057 Hartree with C₁ symmetry (anti4)

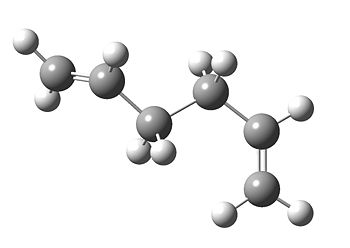
Surprisingly, the anti C₁ conformer is not lower in energy than the gauche C₁ as expected. In fact it is higher in energy than the one of the gauche C₂ conformers and the anti C_i. The most likely explanation for this is stabilising electronic interactions which are present in some conformers (due to better orbital overlaps) but absent in others. This result suggests that steric factors are not all that need to be taken into account when predicting the relative stabilities of different conformers.

It is also worth noting that the energies calculated above are in very good agreement with those reported in the script.

The anti C_i was then re-optimised using the B3LYP DFT method and the 6-31G(d) basis set. This is a higher level of theory and should give a more accurate result.

The DFT calculation took 3 minutes and 21 seconds, as opposed to 1 minute and 9 seconds for HF, owing to the greater level of complexity in density functional theory. The optimised molecule with B3LYP/6-31G(d) looks (by eye) identical to the HF/3-21G result and most the the bond lengths and angles are almost exactly the same (to 1 or 2 decimal places). However, the C=C-C-C dihedral angles and overall energies are significantly different. These values are tabulated below.

	HF/3-21G	B3LYP/6-31G(d)
C=C-C-C dihedral angles in degrees	114.660	118.492
Energy in hartrees	-231.69253506	-234.61172182

These noticeable differences make it clear that as long as there is sufficient time for the longer computation, it is worth using a higher level of theory to obtain as accurate a result as is possible.

The next step was to do a frequency calculation on the anti C_i conformer which gives us further useful data for the energy of the molecule by looking the the "thermochemistry" section of the output file. This was, again, done with B3LYP/6-31G(d) and the result is tabulated below.

Energy component	B3LYP/6-31G(d)
Sum of electronic and zero-point Energies	-234.469182
Sum of electronic and thermal Energies	-234.461844
Sum of electronic and thermal Enthalpies	-234.460900
Sum of electronic and thermal Free Energies	-234.500730

These energies are useful when looking at thermodynamic properties of molecules but can also be used in kinetic arguments when calculated in transition state modelling.

The above energies are calculated at 298.15 K (and 1 atmosphere) but we can instruct the computer to calculate them at 0 K. This is done by adding "readisotopes" to the keywords of the input file so that it reads "# freq=readisotopes b3lyp/6-31g(d)". The input file must also be edited so that the top line of the isotopes section of the input file reads "0.0 1.0" to corresponds to 0 K and 1 atmosphere. The result after implimenting these changes is as follows.

Energy component	B3LYP/6-31G(d)
Sum of electronic and zero-point Energies	-234.469182
Sum of electronic and thermal Energies	-234.469182
Sum of electronic and thermal Enthalpies	-234.469182
Sum of electronic and thermal Free Energies	-234.469182

We can see that all the energy terms are now equal to the sum of the electronic and zero-point energies. This is because E = H + RT and G = H - TS and in the above calculation T = 0 .

Running calculations at different temperatures (or pressure) can be useful as once the activation energy is known, we can predict how much heat energy (or pressure) must be applied in order to put the system over the energy barrier.

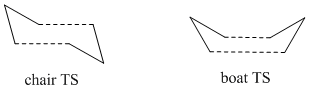
Modelling the Structures of the Boat and Chair Transition States

This part of the experiment will deal with the modelling of the transition state (TS) of Cope Rearrangement, for which there are two possible reaction pathways. The TS itself closely resembles cyclohexane so the rearrangement can occur via a chair TS or a boat TS.

In order two model these two transition states, two allyl fragments are required, so these were optimised using HF/3-21G.

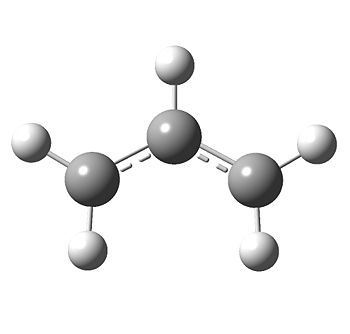
The bond lengths are both 1.38895, demonstrating the delocalised nature of the double bond.

The Chair Transition State

The above allyl fragment was then copied and two were pasted into a new molgroup in Gaussview and orientated so that they resembled a chair TS and so that the bond forming/breaking carbons atoms were approximately 2.2 angstroms apart. A TS(berny) calculation was then run (with a frequency analysis), again using HF/3-21G, but this time the computer was instructed to calculate force constants so that it took the path with the steepest slope on the potential energy surface. The term "opt=noeigen" was also added to the keywords to stop the calculation from crashing if more than once negative frequency occurs. The keywords in the input file ultmately looked like this:

# opt=(calcfc,ts,noeigen) freq hf/3-21g

The resulting TS was the following 3D structure:

chair TS 3qpzm1029

The C-C distances for the bonds that are being broken/formed are 2.02062 angstroms and the energy of the TS is -231.61932223 hartrees.

If we inspect the calculated vibrational frequencies, we observe a negative frequency at -817.724 cm^-1. This confirms that we have indeed found a transition state as these negative value corresponds to the second derivate of the potential energy curve, which is always negative at a maximum critical point. By looking at the form of the vibration (by animating in Gaussview), it can be illustrated by drawing in the displacement vectors.

We can see that this vibration follows the path of the bond breaking and bond forming. This can be shown further by showing vibrations at their greatest magnitudes of displacement.

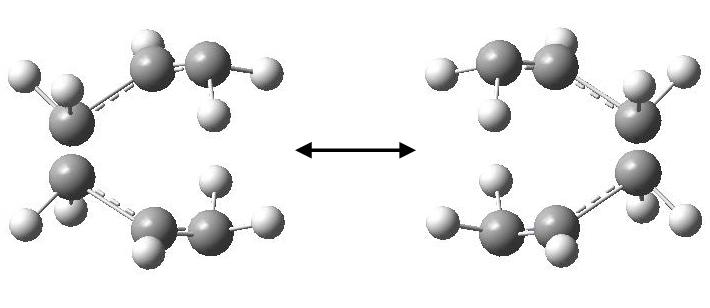
This illustrates further that the negative vibrational frequency is due to the fact that we have found a transition state.

There is another method we can use to model TS structures which utilises the "redundant co-ordinate editor". Two new allyl fragments were pasted into a molgroup and the redundant co-ordinate editor was used to manually freeze the terminal C-C bond distances between the two fragments at 2.2 angstroms. Now that these bonds are frozen, we can optmise this structure to a minimum as if it were a ground state structure for the set C-C distances will not move from 2.2 angstroms. The input file keywords contained an extra term "opt=modredundant" which tells the computer this. The keywords read:

# opt=modredundant hf/3-21g

Obviously the distances are not exactly 2.2 angstroms so we must input a further calculation. In the redundant co-ordinate editor, the bonds previously set to be frozen are now set to be differentiated along so that they are optimised along with the rest of the TS structure. The input file is then set to optimise to TS(berny), with frequency analysis, in the same way as in the first method, but this time with force constant information as the Guess Hessian employed by the bond differentiation negates this. The input keywords now read:

# opt=(ts,modredundant,noeigen) freq hf/3-21g

The C-C distances for the bonds that are being broken/formed are 2.02070 angstroms and the energy of the TS is -231.61932239 hartrees.

In addition the single negative frequency was found to be at -817.759 cm^-1.

The above results are very similar, demonstrating that both methods are sufficiently reliable when it comes to optimising TS structures and finding their vibrational frequencies.

The Boat Transition State

The structure of the boat transition state will be found with yet another different method: QST2. With QST2, we are required to build the structures of the reactants and the products and then the computer will interpolate between them to find the TS. This will be done with anti C_i conformer which was optimised earlier.

The first thing that was done was to copy the anti C_i conformer and paste it into a new molgroup and then add (not append) a second copy to that same molgroup so that they can be view next to each other. Then the labels of each atom were altered so that they corresponded to their positions and connectivity both before and after the rearrangement. This is important as a QST2 calculation will not be available otherwise (because gaussview will not see the two structures as reactants and products). The renumbered structures are shown below.

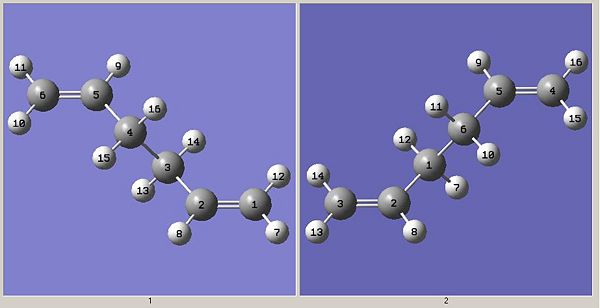
The QST2 calculation was then run with the following input keywords:

# opt=qst2 freq hf/3-21g

However, the result looked rather unusual and was not as expected.

QST2 first 3qpzm1029

As we can see, it appears that the 1,5 hexadiene molecule tried to rearrange by translation rather than by twisting around bonds. carbons 1, 2 and 3 have been translated above carbons 4, 5 and 6, but retained the connectivity between 3 and 4, and made a connection between 1 and 6. If we were to ignore the crossed bonds, this TS would have looked much like the chair TS. but with the terminal carbons 3.18904 angstroms apart, it is much more dissociated.

It is clear that in order to get a correct boat TS, the 1,5 hexadiene molecule needs to be modified so that it looks more like the boat TS. The dihedral angles for carbons 2-3-4-5 in the reactant and 2-1-6-5 in the products was set to 0 degress. Additionally, the bonding angles around carbons 2 and 5 in the reactant and product were set to 100 degrees so that they looked like the screenshot below.

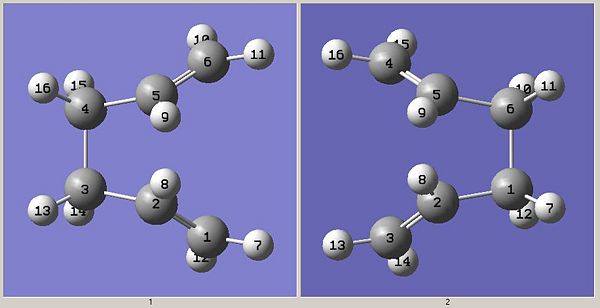
The same calculation was then run which gave the following TS:

QST2 second 3qpzm1029

The structure now looks like a boat TS so the calculation was successful. The C-C distances for the bonds that are being broken/formed are 2.13985 angstroms and the energy of this TS is -231.60280248 hartrees. The C-C distances are longer and the n energy is higher than then chair TS which is what we would expect due to the eclipsing of the central carbon atoms in the two allyl fragments.

In addition the single negative frequency was found to be at -839.936 cm^-1. This frequency is lower than for the chair TS which is also expect for the same reason as the bond lengths, and weaker bonds means lower vibrational frequencies. The form of the vibrations shows the forming and breaking of bonds in the exact same manner as in chair TS so it won't be displayed again.

There is one final method which can be used to find transition states which works in a very similar way to QS2, except we don't need to put the reactant and product into approximate TS orienations. Instead, we add one additional structure to the molgroup which resembles the TS, which is shown below.

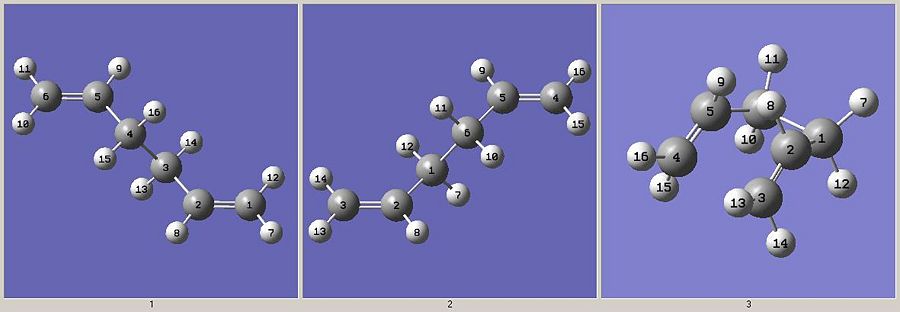
This type of calculation is called QST3 and can often give a better result. The input file was as follows:

# opt=qst3 freq hf/3-21g

The resulting structure again looked like a boat TS and was indistinguishable by eye from the one found by QST2. However, the quantitative results from QST2 and QST3 can be compared.

	QST2	QST3
Forming/Breaking C-C distances in angstroms	2.13985	2.13966
Energy of TS in hartrees	-231.60280248	-234.60280238
Imaginary frequency in cm-1	-839.936	-840.040

The results are almost exactly the same, indicating that both methods are sufficiently reliable. The main advantage of QST3 is that the reactants and products don't need to be moved into approximate TS orientations so it is less likely that the calculation will fail and indeed, it was successful on the first attempt in this case.

Connecting the Transition State to a 1,5 Hexadiene Conformer

By simply looking at the transition state itself, it is nearly impossible to predict which conformer of 1,5 hexadiene it leads to. Therefore we must employ a technique which allows us to follow the path of the reaction along the potential energy surface so that we can see the conformation of the product (and hence the reactant). This technique which we will use it the intrinsic reaction coordinate (IRC) method, which allows us to do just that.

Starting with the chair TS which was optimised earlier using the frozen coordinates method, the following keywords were submitted:

# irc=(forward,maxpoints=50,calcfc) hf/3-21g

As we can see, force constants were calculated once at the start of the calculation and the computer was instructed to run 50 points.

Once the calculation ended, a structure that wasn't much different from the original chair TS. Looking at the IRC energy plot shed some light as to why this happened.

As we can see, the calculation only ran for 14 points, so the structure was not able to fully optimise to the 1,5 hexadiene product. The most likely reason for this is that the computation didn't follow the correct path on the potential energy surface. When this is the case, calculating force constants at every step is usually a suitable solution as it ensures the calculation always follows the path with the steepest slope. Thus, the input keywords were modified to read:

# irc=(forward,maxpoints=50,calcall) hf/3-21g

It should be noted that calculating force constants at every step in this manner is computationally expensive, but in this case the molecule we are investigating does not have that many electrons (compared to bigger structures) so the calculation took only 50 minutes on the SCAN server.

The resulting structure now looked more like a 1,5 hexadiene than two allyl fragments in a transition state. Upon closer inspection, it could be seen that the structure currently in between both of the gauche C₂ conformers found earlier, suggesting that the calculation had still not reached a minimum.

Here is the energy plot:

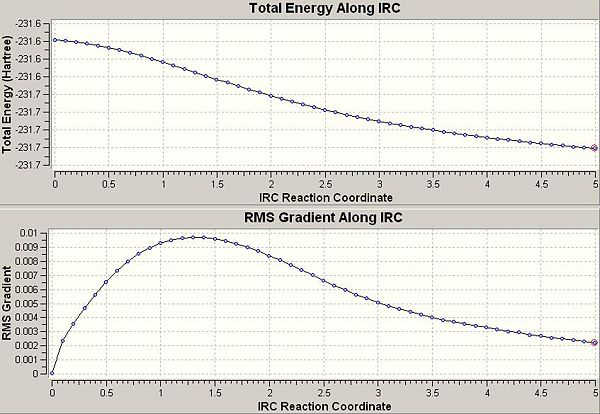
Indeed, a minimum has still not been reached. It seems that 50 points were not sufficient to reach a minimum so we could re-run the calculation and specify more points. However, we are close enough to a minimum that we can simply run a normal optimisation (to a minimum). This yielded the structure below:

chair IRC 3qpzm1029

This looks very similar to the second gauche C₂ conformer calculated at the start of the experiment, and looking at the energy, it is found to be -231.69166702 hartrees, which is very close to the energy of gauche2 in "Appendix 1" of the course wiki. In fact, it is even closer than that of the gauche C₂ conformer calculated previously.

The IRC technique can also be used with the boat TS to see what conformer of 1,5 hexadiene it leads to. The exact same method of running an IRC with all force constants followed by a standard optimisation was used here as with the chair TS. The result was the following structure:

boat IRC 3qpzm1029

This looks very similar to the gauche C₁ conformer calculated at the start of the experiment. It's energy is -231.69226122 hartrees which is exactly the same as both the value found earlier and that of gauche3 in "Appendix 1" of the course wiki.

We can see that this IRC technique is very useful in determining what conformation of products are given by a certain transition state but we can also tell what conformation(s) is/are reactive if we were to run an IRC for the backwards reaction (which would give the same result for the cope rearrangement).

Calculating the Activation Energy

By finding the difference between the energies of ground state 1,5 hexadiene and the transition state, we will have calculated the activation energy for the Cope Rearrangement. This can be done separately for both transition states to find activation energies for the rearrangement via the chair TS and the boat TS.

The first thing to think about is which conformer to use as ground state 1,5 hexadiene. This is not trivial as the molecule is constantly vibrating and will be changing conformation constantly, thus causing many different value for the activation energy to emerge. For this reason, we will pick the low energy, anti C_i conformer as our ground state molecule as once this conformer has enough energy to rearrange, it must be true that the other conformers will also have enough energy.

In addition, we remember that the energy of the anti C_i conformer was vastly different when calculated with B3LYP/6-31G(d) compared to HF/3-21G. Therefore, it is wise to re-optimise the chair and boat transition states using the higher level of theory so that we can make a better comparison. The higher level calculation made little difference to the geometry, but the energy was markedly different.

Energy in hartrees	HF/3-21G	B3LYP/6-31G(d)
Chair TS	-231.61932239	-234.55698297
Boat TS	-231.60280238	-234.54307898

Due to this significant difference, it is worth finding separate activation energies for both levels of theory so that we can make a comparison and see if they result in the same value. In the script, we are given literature values of 33.5 ± 0.5 kcal/mol for the chair TS and 44.7 ± 2.0 kcal/mol for the boat TS at 0 K. For this reason, we will calculate the activation energy at 0 K by looking using the zero-point energies in the "thermochemistry" section of the log file. Frequency calculation were run on the anti C_i conformer of 1,5 hexadiene with both methods and basis sets in order to do make the comparison at 0 K.

	Chair TS with HF/3-21G	Boat TS with HF/3-21G	Chair TS with B3LYP/6-31G(d)	Boat TS with B3LYP/6-31G(d)
Energy in hartrees	-231.466701	-231.450926	-234.414927	-234.402324
Energy of 1,5 hexadiene (anti Ci) in kcal/mol	-231.539542	-231.539542	-234.469182	-234.469182
Difference from energy of 1,5 hexadiene (anti Ci)	0.072841	0.088616	0.054255	0.066858
Difference converted to kcal/mol	45.71	55.61	34.05	41.95

The activation energies found with HF/3-21G do not match well with the literature values of 33.5 ± 0.5 kcal/mol for the chair TS and 44.7 ± 2.0 kcal/mol for the boat TS. However, once the theory level was increased to B3LYP/6-31G(d) the agreement was much better. The values do not match exactly but they are quite close, given the degree of error in the literature. This shows us that the accuracy increases significantly when a higher method and basis set is used.

The match between the theory and experiment would probably be even better if we were to use, perhaps MP2/6-311G(d), however we do not have time to do this in this experiment and we have already demonstrated that computational techniques are very useful in predicting experimental quantities to reasonable accuracy.

Comparing the activation energies of the two transition states, we have calculated the chair TS to be 7.90 kcal/mol lower than the boat TS. Therefore, given that the reactants and products have equal thermodynamic stability (because their structures are identical), we can logically predict that the Cope Rearrangement prefers to proceed via the less energetic chair transition state, and will twist into the required gauche C₂ conformer in order to do so.

It is also interesting to note that even though the gauche C₂ conformer (for the chair TS) is higher in energy than the gauche C₁ conformer (for the boat TS), it is closer to the energy barrier of its corresponding transition state so we would expect to find more 1,5 hexadiene in this conformation immediately before and after the rearrangement.

In his book, "Frontier Orbitals and Organic Chemical Reactions", Ian Flemming offers a frontier orbitals explanation for the lower energy of the chair TS. He suggests that there is a secondary anti-bonding interaction between the HOMO and LUMO orbitals of the two allyl fragments in the boat TS which destabilises this transition state with respect to the chair TS, where there is no such anti-bonding interaction.

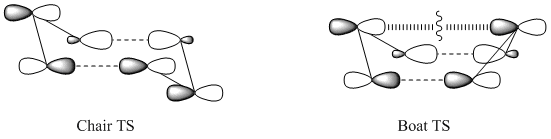
This explanation supports the results of the experiment, which predicted the chair TS to be 7.90 kcal/mol more stable than the boat TS. The role of secondary orbital interactions such as this will be discussed in the next exercise.

The Diels Alder Cycloaddition

Like the Cope Rearrangement, the Diels-Alder cycloaddition is a pericyclic reaction, but it is one that is often dominated by the so-called "endo rule" which predicts that Diels-Alder products form with predominantly endo isomerism. In this part of the experiment, we will use molecular modelling with a heavy emphasis on molecular orbital calculations, to investigate the origin of the endo rule.

The Reaction of Ethene with Butadiene

First of all, we will model the simplest Diels-Alder reaction, which is the formation of cyclohexene from butadiene and ethene.

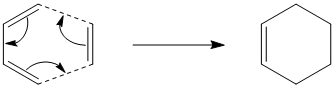
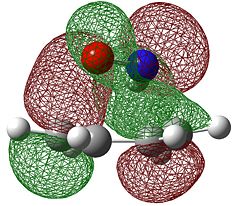
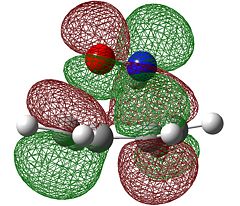
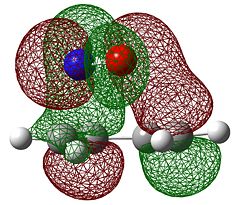
When considering Diels-Alder reactions, it is important to note that they occur by the overlap of the HOMO of one Diels-Alder adduct and the LUMO of the other. In order for this overlap to be allowed, they must be of the same symmetry. For this reason, we will visualised the orbitals of ethene and butadiene to determine whether they are symmetric or antisymmetric with respect to the plane. Butadiene and ethene were optimised using the semi-emperical AM1 method, which gave the following results.

	Ethene HOMO	Ethene LUMO	Butadiene HOMO	Butadiene LUMO
Quantitative MOs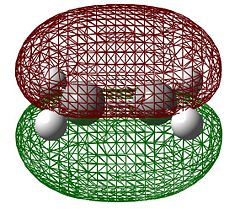
Qualitative MOs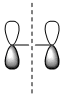
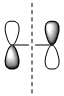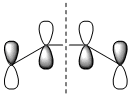Symmetry with respect to the plane	symmetric	antisymmetric	antisymmetric	symmetric

We can see from the table above that the symmetries of the ethene HOMO and butadiene LUMO are the same, as are the ethene LUMO and the butadiene HOMO, therefore the reaction is allowed.

The transition state of the reaction was then modelled using the freeze coordinate method (setting the forming C-C bond to 2.2 angstroms, followed by the derivative calculation) used in the previous exercise. The TS was first calculated with the AM1 method, followed by B3LYP/6-31G(d).

butadiene 3qpzm1029

The forming C-C bonds are 2.27216 and 2.27203 angstroms which are very similar lengths, suggesting that the bond forming mechanism is synchronous. We can compare these with known values for C-C bond lengths and the carbon Van der Waals radius.

C-C bond length	1.54 Å
C=C bond length	1.34 Å
Van der Waals radius of carbon	1.70 Å

Clearly, the C-C distances we are considering are nowhere near a fully fledged covalent bond, but they are quite a lot smaller than two times the Van der Waals radius of a carbon atoms (3.40 Å). This means the Van der Waals spheres of the carbon atoms are overlapping, owing to the partially formed bonds in the transition state. In simple terms, this confirms to us that the C-C bond lengths we have obtained in the above structure is due to a state somewhere in between that of two separate reactant molecules and fully formed covalent bonds in the product, i.e. a transition state.

As expected for any transition state, there was one negative vibrational frequency. This was found at -525.162 cm^-1 and the form of the vibration is shown below.

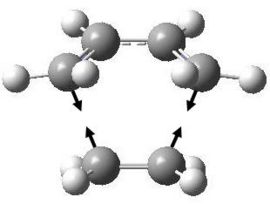
Again, we can see that the bonds are formed in a synchronous fashion. This is further demonstrated by showing the vibration at different stages of displacement.

If we look at the first positive vibration at 135.919 cm^-1, it is a rocking of the ethene fragment underneath the butadiene fragement. This can be shown by a screenshot of the TS with displacement vectors included:

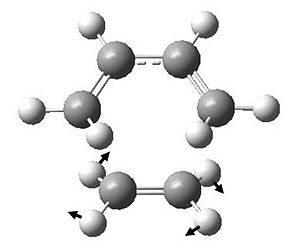
It is clear that this vibrational has no relation to the formation of new bonds.

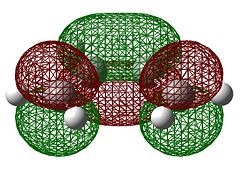
The molecular orbitals of the transition state were then visualised. Below are the results from an AM1 calculation.

	HOMO-1	HOMO	LUMO
Quantitative MOs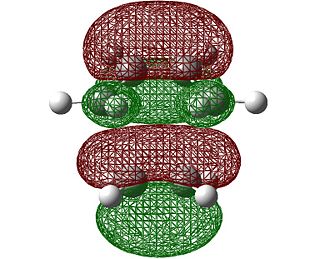
Qualitative MOs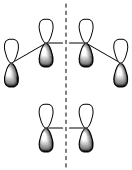
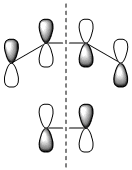Symmetry with respect to the plane	symmetric	antisymmetric	symmetric

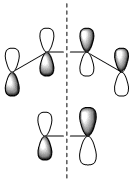
The fact that the HOMO is antisymmetric with respect to the plane suggest that it arises from the overlap of the butadiene HOMO and ethene LUMO. In a similar fashion, the symmetric transition state LUMO suggests that it comes from overlap of the ethene HOMO and butadiene LUMO. These suggestions are also supported by simply inspecting the shape of the graphical representations of the calculated MOs.

It can be seen that the suprafacial overlap of the orbitals in the HOMO corresponds to the well-defined selection rules for pericyclic reactions, which state that reacting systems containing 4N+2 electrons (N=1 in this case) proceed via a Hückel transition state (i.e. no twisting of the orbitals is required) and overlap suprafacially as they have done in the above example.

The reason the results from the AM1 calculation are shown in the table (and not B3LYP/6-31G(d)) is because this corresponds to what we would naturally expect to be the case i.e. the HOMO of the TS to be the result of an overlap between the HOMO and LUMO of the starting materials. However, upon increasing the level of the calculation to B3LYP/6-31G(d), it was observed that the relative levels of the HOMO and the HOMO-1 swapped over. It can be seen that the HOMO and the HOMO-1 are in fact very close in energy:

	AM1	B3LYP/6-31G(d)
HOMO energy in a.u.	-0.323	-0.218
HOMO-1 energy in a.u.	-0.325	-0.221

This closeness in energy is probably due to the fact that in this reaction neither the diene or the dienophile can really be classified as electron rich or electron poor as there are no electron donating or withdrawing groups. Despite the change in the ordering of the HOMO and HOMO-1 in the transition state, this does not change the ordering and hence the symmetries of the HOMOs and LUMOs of the two reactants, therefore the fact remains that this is an allowed reaction.

The Reaction Cyclohexa-1,3-diene and Maleic Anhydride

The next reaction to be studies is the Diels-Alder cycloaddition between cyclohexa-1,3-diene and maleic anhydride. This is very similar to the previous example in that it is also a [4+2] cycloaddition, but time there are substituents on the diene and the dienophile so the product can form with either exo or endo isomerism. We will attempt to use molecular orbital interactions to rationalise the observed stereochemistry of the "endo rule".

Here is the reaction scheme:

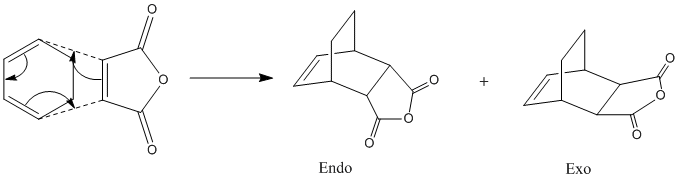
We know from the endo rule that Diels-Alder reactions are typically under kinetic control and thus the endo isomer is the one that dominates so it is logical to predict the the endo TS will be the one with the lowest energy. Hopefully, calculating the orbitals themselves will help shed some light on the reason for this preference.

The transition states for both the endo and exo isomers were calculated were first calculated at the AM1 semi-empirical method using the freeze coordinate technique, followed by taking derivatives along the forming C-C bonds. The TS structure was then further optimised with B3LYP/6-31G(d) and because there was adequate time, a final optimisation using the more accurate MP2/6-311G(d) basis set was administered in order to obtain an accurate a result as possible. The final TS structures are below.

Exo TS:

MA Exo TS 3qpzm1029

Endo TS:

MA Endo TS 3qpzm1029

The Exo TS has a negative vibration at -332.520 cm^-1 and the endo TS has a negative vibration at -314.777 cm^-1, which confirms that we have found a pair of transition state structures. The form of both vibrations is totally analogous to the reaction between ethene and butadiene in that they correspond to the path of synchronous bond formation between the CH=CH fragment on maleic anhydride and the CH=CH-CH=CH fragment on cyclohexa-1,3-diene. For this reason, there is no need to show screenshots with displacement vectors again.

Looking at the above structures, we can tabulate some internuclear distances which are of particular interest as well as the energy of the TS using the advanced MP2/6-311G(d) model.

For the exo isomer:

Atoms involved	Sketch showing distance being considered	Internuclear distance in angstroms
Forming C-C bond distance		2.36792 and 2.36835
Through space C-C distance		2.95067 and 2.94976
Through space C-H distance		2.44170 and 2.43879
Overall energy of this TS in hartrees	-611.32079634

For the endo isomer:

Atoms involved	Sketch showing distance being considered	Internuclear distance in angstroms
Forming C-C bond distance		2.35890 and 2.35868
Through space C-C distance		2.86594 and 2.86574
Through space C-H distance		2.95163 and 2.95118
Overall energy of this TS in hartrees	-611.32604544

Not surprisingly, the endo isomer is more stable than the exo by 3.29 kcal/mol. In order to compare with the literature, the activation energies will be calculated from the B3LYP/6-31G(d) results.

	Exo TS	Endo TS
Energy of the starting materials in hartrees	-612.7084546	-612.7084546
Energy of the TS in hartrees	-612.6793108	-612.6833967
Activation energy in hartrees	0.02914372	0.02505789
Activation energy in kcal/mol	18.29	15.72

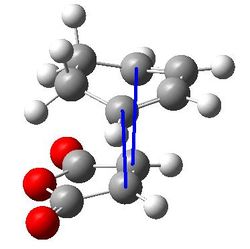
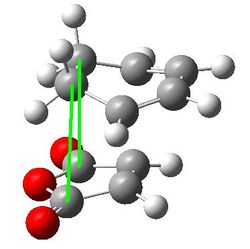
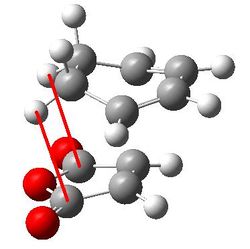
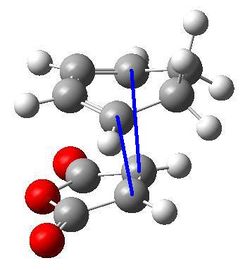
Our B3LYP/6-31G(d) calculation has predicted the endo TS to be 2.57 kcal/mol lower in energy than the exo TS. A literature value for this exact reaction could not be found, but a very similar reaction, between maleic anhydride and cyclopentadiene, was found, and our energy is in very good agreement with this literature value of 2.5 kcal/mol. This same article also reports that the product mixture is almost exclusively endo, consisting of 98.5% endo product, suggesting that the kinetics of the reaction is important. We can compare some of the C-C and C-H distances between the two isomers to help explain this clear endo preference.

The forming C-C bonds are slightly shorter than in the endo case. More significantly, there is a fairly large difference in the C-C through space distance marked in green (shorter for endo) and an even larger difference in the C-H distance marked in red (shorter for exo).

The main distinction between between the two isomers, geometry-wise, is the hybridisation of the carbon atoms above the O=C-O-C=O fragment in the maleic anhydride. In the endo TS they are sp², while they are sp³ in the exo TS. The tetrahedral sp³ carbons end up pointing a pair of hydrogens towards the maleic anhydride ring which results in greater steric repulsion, and hence an increased TS energy and a larger C-C through space distance as reported.

This is a clear factor for the preference of endo stereochemistry over exo, but even though sterics do explain the reason for a shorter through space C-C distance (marked in green), we must consider whether or not this shorter distance can be accounted for by electronic effects.

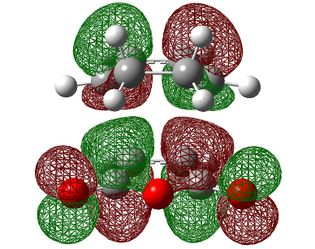
Here are the calculated molecular orbitals for both isomers:

	HOMO-1	HOMO	LUMO
Exo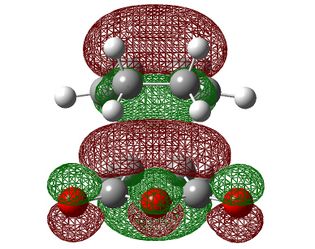
Endo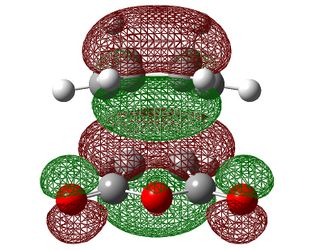
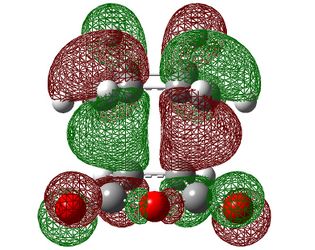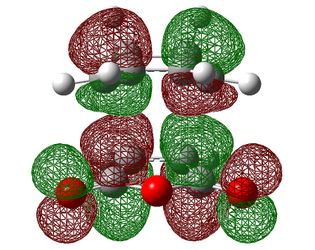Symmetry with respect to the plane	symmetric	antisymmetric	symmetric

Firstly, we can see that the orbitals here are analogous to those in the TS between ethene and butadiene with identical symmetries so this is therefore also a suprafacial orbital overlap. One area to take note of, however, is that fact that unlike in the previous reaction, the the ordering of the HOMO and the HOMO-1 did not change as the level of theory was increased. This is probably down to the presence of electron withdrawing groups on maleic anhydride which strongly define it as the electron poor component.

In order to support the shorter C-C through space distances in the endo TS, we would expect to see something like the following:

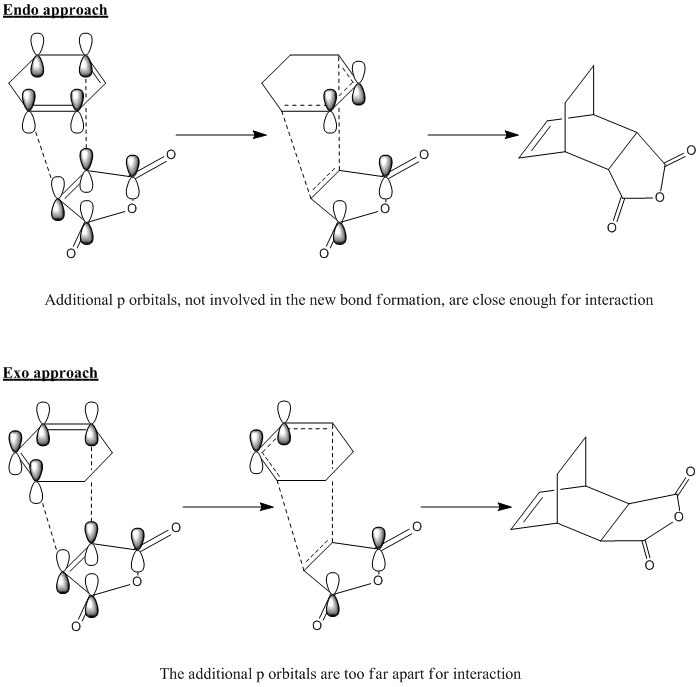
Looking for any evidence of any stabilising effect between the the two carbon atoms not involved in bond forming doesn't really yield any obvious interaction. The closest case of a secondary orbital interaction is in the HOMO-1 of the endo TS where the forming C=C bond in the six-membered ring is close to a similarly-phased orbital on the carbonyl oxygens, but this is surprising as we would have expected any such interaction with the C=O π* orbital to be through the carbonyl carbon as it is closer in distance. Even so, these similarly-phased orbitals do not actually overlap, which contradicts the above qualitative diagram.

Even though there is not full-blown overlap, there might still be some sort of attractive interaction between the orbitals. In order to ascertain whether or not this is the case, a full NBO anylsis was run on the B3LYP/6-31G(d) level (for comparison with the literature) using the following keywords:

# B3LYP/6-31G(d) pop=nbo

Gaussview is unable to visualise most of the results from an NBO analysis so the log file was opened and the section giving the results of the second order perturbation theory analysis. This quantifies the resulting stabilisation which arises from the overlap of orbitals in the system.

The orbital overlaps we are interested in are those between the C=C π bonds in the diene and the C=O π* bonds in the maleic anhydride and the results for these are shown below.

Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis

    Threshold for printing:   0.50 kcal/mol
   (Intermolecular threshold: 0.05 kcal/mol)
                                                                             E(2)  E(j)-E(i) F(i,j)
        Donor NBO (i)                     Acceptor NBO (j)                 kcal/mol   a.u.    a.u. 
===================================================================================================
...
21. BD (   2) C  13 - C  18         /199. BD*(   2) C   4 - O   9            1.87    0.28    0.021
...
24. BD (   2) C  15 - C  20         /191. BD*(   2) C   1 - O   8            1.86    0.28    0.021

As we can see, there is indeed some sort of stabilising interaction of the order of 1.86 and 1.87 kcal/mol. The literature reports 1.48 kcal/mol. The log file for an identical NBO calculation on the exo TS shows no C=C π to C=O π* interaction at all.

So secondary orbital overlaps do play a role in the shorter C-C distances and hence the more stable endo TS. But is their role more significant than the increased exo steric repulsion in explaining the endo preference? An attempt was made in quantifying the pairwise steric exchange energy between the atoms involved in the secondary orbital interaction by following the example found here.

A calculation was submitted with the following keywords:

#N B3LYP/6-31G(d) pop=nboread

And at the end of the input file, the followng was added:

$NBO steric $END 

However, the calculation crashed with the error in the log file:

Error: Unrecognisable keyword >>STERIC<<

After consutling the NBO faq page (Q2), it seems that NBO 5.0 is required for steric analyses, whereas Gaussian 03 only has NBO 3.1 built-in.

It is unfortunate that we are unable to run the calculation, but a literature value of 3.47 kcal/mol was found. If we compare this to the value calculated earlier, it is slightly larger, and the overall effect is repulsions of 1.61 and 1.60 kcal/mol. This explains why we see no orbital overlap in the visualised MOs and also why there is a relatively large through space C-C distance of ~2.87 angstroms.

So we can see that while there is indeed an attractive force between the secondary orbitals in question, this is overcome by the closed-shell exchange repulsion between the carbon atoms. We can therefore suggest that the force leading to the endo preference in the TS is not attractive, but repulsive, of which this is greater in the exo TS, due to close proximity of the O=C-O-C=O fragment to the protons on the above sp³ hybridised ethylene carbons in the exo approach.

It is also worth noting that in addition to the endo TS being the more stable TS, the endo product has also been calculated at the MP2/6-311G(d) level to be 1.78 kcal/mol lower in energy than the exo product. We can draw an approximate reaction pathway:

This points out that whether the reaction is kinetically or thermodynamically controlled is not really important as it will always lead predominantly to the more thermodynamically stable endo product. The increased thermodynamic stability of the endo product is most likely down to the same, decreased steric repulsion (compared to the exo TS) we pointed out its transition state, which lead to a more stable endo TS.

The energy gap between the transition states of 2.57 kcal/mol, however, is slightly larger than the product energy gap, which is thought to be the sum of decreased steric destabilisation (as in the product) and the somewhat less dominant electronic stabilisation (from secondary orbital interactions) in the endo TS, which arose from our TS analysis.

A Further Example: The Diels-Alder Reaction Between HNO and Butadiene

The example we have investigated so far have all had a plane of symmetry and the bonds formed have been between atoms of the same type, with the same substituents. Now we will look at the effect of reacting two Diels-Alder adducts which lead to a non-symmetrical TS.

The example to be considered is the reaction between HNO and butadiene, which has already been the subject of study by Houk and Leach. The reaction scheme is shown below.

Endo Vs Exo selectivity

The issue we will first focus on is, like before, which of the exo and endo TS are the most stable and also to try and explain why this might be.

Because the two components are unsubstituted and relatively small, simple steric repulsion is not likely to play such a big role, especially due to the fact that the presence of sp² carbons in both transition states minimises clashes with protons. We will therefore first examine the molecular orbitals.

The orbitals of HNO and butadiene have been calculated to the B3LYP/6-31G(d) level and are shown below to see which are likely to overlap. Because HNO will have lobes of unequal size we will characterise it as if they were equal size and state its approximate pseudo-symmetry.

	HNO HOMO	HNO LUMO	Butadiene HOMO	Butadiene LUMO
Quantitative MOs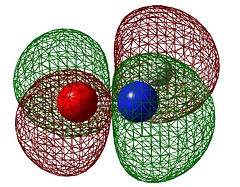
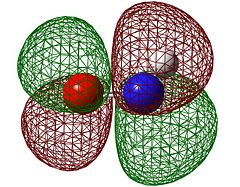Qualitative MOs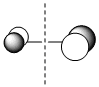
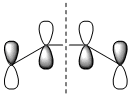Symmetry with respect to the plane	antisymmetric	antisymmetric	antisymmetric	symmetric

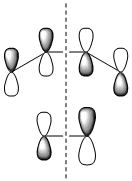
It is straight away obvious that both the HOMO and LUMO on HNO are antisymmetric while only the HOMO is antisymmetric in butadiene. The origin of this is the fact that unlike ethene, HNO has lone pairs on nitrogen and oxygen, and the HOMO is the anti-bonding combination of these lone pairs rather than the N=O π orbital. This means that there will only be one "allowed" overlap and in order for the other pair of orbitals to overlap they will have to go through a Möbius transition state.

The two transition state isomers were calculated using the same method used in the previous exercise (frozen coordinates followed by derivative), first with AM1 and then with B3LYP/6-31G(d). Here are the resulting TS structures:

Exo isomer:

HNO exo 3qpzm1029

Endo isomer:

HNO endo 3qpzm1029

We can now calculate the (zero-point) activation energies for each TS to see which is most stable.

	Exo TS	Endo Ts
Energy of the starting materials in hartrees	-286.355079	-286.355079
Energy of the TS in hartrees	-286.338405	-286.352209
Activation energy in hartrees	0.016674	0.002870
Activation energy in kcal/mol	10.46	1.80

Interestingly, the endo TS activation energy has been calculated to be 1.80 kcal/mol which is quite low compared to the energies found in the previous exercises. This isn't too surprising, however, considering the instability of HNO, which readily dimerises to H₂N₂O₂. Not so surprisingly, the endo TS is 8.66 kcal/mol more stable than the exo TS. Leach and Houk found a difference of 8.6 kcal/mol. In order to explain this energy difference, we will consider the molecular orbitals.

The orbitals of both transition states have been visualised. The quantitative MOs may be rotated to a slightly different orientation to the qualitative MOs in order to make the nodal properties easier to see.

	HNO exo TS HOMO	HNO exo TS LUMO	Butadiene endo TS HOMO	Butadiene endo TS LUMO
Quantitative MOs
Qualitative MOs
Symmetry with respect to the plane	antisymmetric	antisymmetric	antisymmetric	antisymmetric

The calculated orbitals are somewhat difficult to interpret, but those of the endo TS seem to match the qualitative ones reasonably well, however those of the exo TS do not match the qualitative MOs very well, which is because the symmetry of the orbitals were not such that they gave an "allowed" overlap. As a result, they had to overlap antarafacially, which is apparent in the exo TS by the twisting of the orbitals.

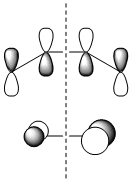
One explanation for the endo preference is electrostatic repulsion between the nitrogen lone pair and the π electrons in butadiene. A complimentary explanation uses frontier molecular orbitals. In a typical Diels-Alder reaction, a HOMO-HOMO overlap is usually forbidden, but in this case there is an allowed, unfavourable interaction in the exo approach between the HNO HOMO and the diene HOMO as they are of the correct symmetry for overlap. Leach and Houk illustrate this with the following qualitative diagram:

However, this is not quite right as this suggests that both oxygen lone pairs are in a single p orbital, when in fact they are in separate sp² orbitals as the oxygen p orbital is tied up in the N=O π bond (with the nitrogen p orbital). We can therefore modify the digram slightly:

Despite the modification of the diagram, the explanation remains unchanged. In the endo approach the nitrogen lone pair is pointing away from the diene π orbitals, so the unfavourable HOMO-HOMO interaction is minimised. It is interesting to note that with this explanation, the driving force for endo selectivity is once again repulsive and not attractive, such as it was in the reaction between cyclohexa-1,3-diene and maleic anhydride.

And from the results of this experiment, an additional factor may well be the fact that the overlap for the exo TS is not a fully allowed reaction. Usually [4+2] cycloadditions are symmetry allowed reactions, but this assumes HOMOs corresponding to π orbitals and LUMOs corresponding to π* orbtals. Here, the HOMO of HNO is the antibonding combination of its lone pairs, which breaks the symmetry possessed in the analogous reagent, ethene. For this orbital to overlap with the antisymmetric LUMO of butadiene in the exo approach, an antarafacial component is required, whereas the endo TS arises from direct, suprafacial interaction which is the standard mechanism of reaction for a [4+2] (6 electron) cycloaddition under thermal conditions. These calculations were restricted closed shell, so triplet states for photochemical conditions were not allowed.

Synchronous or Asynchronous Mechanism

Another aspect of this reaction to consider is the degree of synchronicity of the bond formation. The examples in the previous exercise have been symmetric and the new bonds were of the same type with identical substituents, so it was a concerted, synchronous cycloaddition. In this, unsymmetric pericyclic system it is unlikely that the bonds will form to the same degree in the same amount of time. The scheme below represents the possibility of synchronous or asynchronous bond formation.

We can get a quick, rough representation of the reaction path by looking at the negative vibrational frequencies of the transition states.

The endo TS has the following vibration at -237.753 cm^-1:

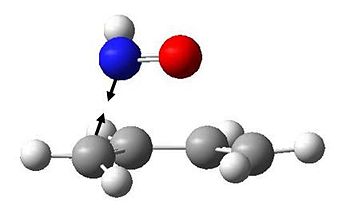
We can illustrate the motion of this vibration by showing two snapshots at maximum displacements:

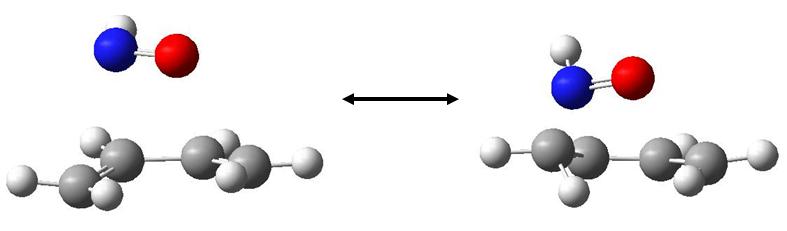
It is clear that this is highly asynchronous, and suggests an almost step-wise bond formation, with the C-N bond forming first.

The exo TS has the following vibration at -344.192 cm^-1:

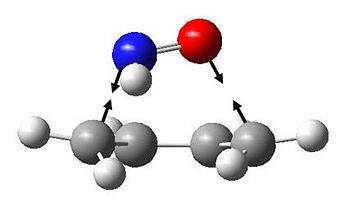
And at maximum displacements:

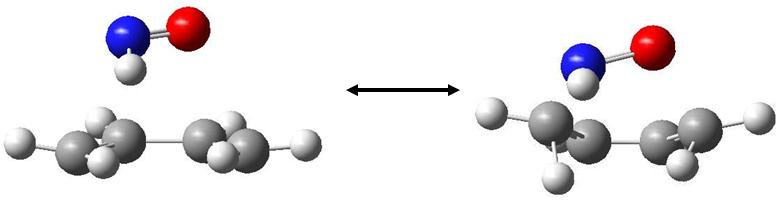
This vibration is much more synchronous, and hence the bond formation follows a more concerted path.

We can investigate the path of bond formation further by considering the C-N and C-O distances in each transition state.

	Exo TS	Endo TS
C-N distance in angstroms	2.04540	2.20945
C-O distance in angstroms	2.04844	2.68812

The C-N distances are very similar in both transition states but the C-O distance is significantly longer in the endo TS. The C-O distance is 0.16405 angstroms longer than the C-N distance in the exo TS, while it is 0.63968 angstroms longer in the endo TS, further demonstrating the highly asynchronous nature. In fact, the endo TS C-O distance of 2.68812 is much closer to the combined Van der Waals radii of carbon and oxygen, 3.22 angstroms, than it is to a typical C-O bond length of 1.43 angstroms. This suggests that there is negligible C-O bond formation in the endo TS.

To explain this highly asynchronous bond formation of the endo TS, we can turn to a similar frontier molecular orbital model we used in the previous section. In the exo approach, the HOMO of the HNO dienophile points two lone pairs towards the diene, whereas in the endo approach, only one lone pair points towards the diene. Overall, the HOMO-LUMO interaction in the endo TS involves less electron density which comes from only one atomic orbital contribution. This leads to a significantly longer C-O distance in the transition state. The qualitative diagram below illustrates this idea.

This theory is supported by an NBO analysis (at the B3LYP/6-31G(d) level).

For the exo TS:

                                                                             E(2)  E(j)-E(i) F(i,j)
        Donor NBO (i)                     Acceptor NBO (j)                 kcal/mol   a.u.    a.u. 
===================================================================================================

103. BD*(   2) N   9 - O  10        / 94. BD*(   2) C   1 - C   5           27.94    0.08    0.068

For the endo TS:

                                                                             E(2)  E(j)-E(i) F(i,j)
        Donor NBO (i)                     Acceptor NBO (j)                 kcal/mol   a.u.    a.u. 
===================================================================================================

103. BD*(   2) N   9 - O  10        / 94. BD*(   2) C   1 - C   5           16.19    0.06    0.050

The exo TS, with two lone pairs in the C=O π* orbital pointing towards the diene LUMO, has a charge transfer energy of 27.94 kcal/mol. On the other hand, the endo TS, which has only one lone pair in the C=O π* orbital pointing towards the diene LUMO, has a charge transfer energy of only 16.19 kcal/mol, so the oxygen atom in HNO isn't pulled towards the diene to as great a degree as it is in the exo approach. This accounts for the varying nature of the HOMO-LUMO interaction in each transition state.

Linking back to the previous section, this NBO analysis shows that based on pure HOMO-LUMO orbital overlap, we would expect the endo TS to be higher in energy (due to less HOMO-LUMO charge transfer). The lower energy endo TS must therefore predominantly come from the repulsive HOMO-HOMO interaction discussed in the previous section. Unfortunately the results from the second order pertubation theory calculations from our NBO analysis only represent attractive interactions, and we're not familiar with any method which quantifies specific orbital repulsions and neither have Leach and Houk reported such a value. However, if we were to run a calculation of this kind we would expect the energy increase from the HOMO-HOMO repulsion in the exo TS to exceed 11.75 kcal/mol (27.94 - 16.19), which is the extra stabilisation from increased charge transfer in the exo TS.

It can be seen that in this particular example, an orbital explanation can be used to account for both (endo) stereoselectivity and also the vastly differing rate of bond formation in the transition state.

Houk and Leach have also investigated the possibilty of zwitterionic and diradical mechanisms leading to asynchronicity. Their proposed reaction scheme is shown below:

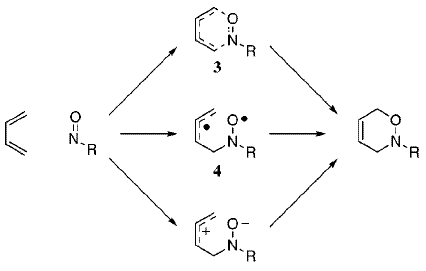
Possible diradical mechanisms could be calculated by unrestricted DFT calculations (allowing unpaired electrons), but there isn't sufficient time to do this. Nevertheless, Houk and Leach concluded from their calculations that "Diradical and zwitterionic pathways only compete when nitroso compounds bearing a small nitrogen substituent react with dienes substituted with radical-stabilizing groups". Therefore, we probably wouldn't have observed any diradical or zwitterionic behaviour as our diene (butadiene) does not possess radical-stabilising groups.

Early Vs Late Transition State

It is notable that the N=O bond lengths in both transition states are still fairly close to their original lengths in HNO. These have been tabulated below for comparison together with the corresponding lengths in the product, which has been optimised at the B3LYP/6-31G(d) level of theory.

	Exo	Endo
N=O distance in free HNO (in angstroms)	1.20743	1.20743
N=O in the TS (in angstroms)	1.25478	1.23033
N-O in the product (in angstroms)	1.45574	1.43652

We can see that the TS N=O distances are in fact a lot closer to the lengths of free HNO than they are to the N-O single bond distances in the product. From this, we can postulate that both TS structures for this reaction correspond to an early transition state. It has also been noted that the N=O lengths are slightly shorter in the endo TS than they are in the exo TS, but we cannot assertively say that this is due to this being an earlier transition state than the exo TS, as the N-O distances are also shorter for the endo product.

In addition, we have found the exo product to be a very (and unexpectedly) large 776.3 kcal/mol lower in energy than the endo TS (at the B3LYP/6-31G(d) level). While there is certainly a contribution from the decreased steric clash between the N-H hydrogen and the rest of the ring atoms, the dominant factor is believed to involve dipole moments.

	Exo	Endo
Dipole moment in the TS (in debeye)	1.3114	2.7093
dipole moment in the product (in debeye)	2.1058	2.1022

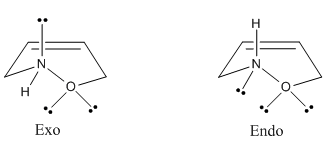
The very large dipole moment of 2.7093 debeye in the endo product differs significantly to the much smaller dipole moment of 1.3114 debeye in the exo product, and this is highly disfavoured energetically. This is in great contrast to the dipole moments for both TS structures, which are very similar. The diagram below shows all the lone pairs on nitrogen and oxygen pointing mostly in the same direction in the endo product, which reinforces (and explains) the large dipole moment.

We can summarise our findings with an approximate energy Vs reaction co-ordinate diagram.

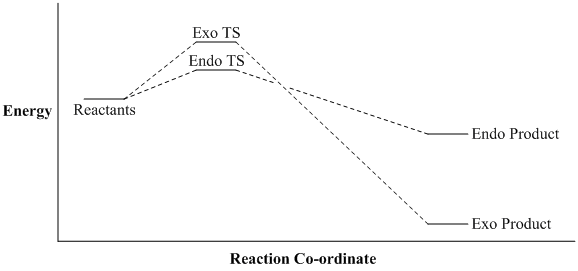
From this experiment we have shown that the endo TS is the most stable, which typically would yield the endo product in a kinetically controlled reaction. However, the far greater thermodynamic stability of the exo product may well override this and favour exo selectivity. It would be interesting, if experimental data for this reaction were to become available, to see whether the exo product forms exclusively as its far superior thermodynamic stability (compared to the endo product) seems to suggest.

An extension to this exercise

HNO has a significant dipole moment of 1.65 debeye so it can be expected that solvent polarity will play a role in the kinetics of this reaction. All the calculations so far have been for isolated molecules (essentially a gas phase model), but a solvated model could be applied be adding the keywords "scrf(solvent=xxxx)" where xxxx is the desired solvent. For example, for water this would be:

scrf(solvent=water)

A series of solvents with varying polarity should be experimented with to explore solvent effects on the reaction kinetics. Unfortunately there is insufficient time to carry out this investigation, but this would be an interesting extension to carry out at some point.

Conclusion

This experiment has shown how computational techniques can be used to probe into the transition state, which is an invaluable tool as transition states are inaccessible to experiments in the lab and are unique to computational chemistry. We have seen how molecular orbitals can play a role in stabilising a particular transition state, and how this effect can sometimes be overridden by repulsive factors; either steric or electronic. In addition, unsymmetrical, hetero Diels-Alder cycloadditions can lead so significant asynchronicity, which in this case can be explained by the orientation of the dienophile's HOMO in its approach towards the diene and its LUMO. Transition state calculations are indeed a useful resource and will no doubt be useful in further experiments.