Rep:Mod:3ir208
Transition state and reactivity
The Cope rearangement tutorial
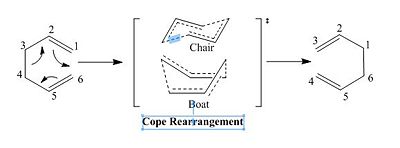
1,5-hexadiene undergoes a thermal isomerization via a [3,3]-sigmatropic rearrangement referred to as Cope rearrangement. The reaction is concerted and pericyclic as it proceeds via cyclic transition state and there are no intermediates on the reaction profile. The transition state has a (4n+2) π electrons Hückel topology and may either be in its chair or boat conformation. This exercise investigate the conformational stability of the 1,5-hexadiene reactant and thus product as well as transition states using both semi-empirical and more accurate quantum-mechanical optimization techniques.
Optimisation of the 1,5-hexadienereactant and product
1,5-hexadiene structures were drawn in Gaussview, and optimized initially using the Hartree-Fock method and a 3-21G basis set. The Dihedral angles of the central carbon framework were set to adjust bond orientations such as to obtain structures with Gauche and Anti conformations at the central C-C bond. All structures were cleaned before performing geometrical optimisations. The table below summarises the structures obtained with their respective point groups and total energy.
| Conformer | Structure | Point Group | Energy/Hartrees HF/3-21G |
Relative Energy/kcal/mol |
| gauche1 | C2 | -231.68772 | 3.10 | |
| gauche2 | C2 | -231.69167 | 0.62 | |
| gauche3 | C1 | -231.69266 | 0.00 | |
| gauche4 | C2 | -231.69153 | 0.71 | |
| gauche5 | C1 | -231.68962 | 1.91 | |
| gauche6 | C1 | -231.68916 | 2.20 | |
| anti1 | C2 | -231.69260 | 0.04 | |
| anti2 | Ci | -231.69254 | 0.08 | |
| anti3 | C2h | -231.68907 | 2.25 | |
| anti4 | C1 | -231.69097 | 1.06 |
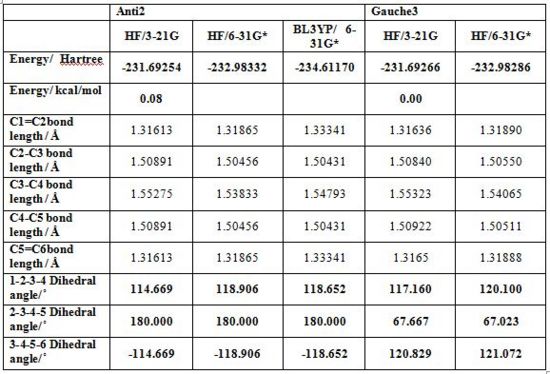
The anti structures are characterised by an antiperiplanar arrangement of the four central carbon atom and were thus modelled setting the central dihedral angle to 180°, and the 2 peripheral to approximately 120°. The first antiperiplanar conformation to be modelled and optimized was in fact the “Anti2” (as given by the tutorial appendix) conformation. Optimisation via a Hartree-Fock method and 3-21G basis set gave Ci symmetry point group and a total energy of -231.69254 Hartrees (0.08kcal/mol) as given in the provided tutorial appendix. The second anti form obtained was the “Anti1” structure with C2 point group symmetry and a total energy of -231.69260 Hartrees (0.04kcal/mol). “Anti3” is obtained by setting the external C-C-C-C dihedral angle to 0° yielding a synperiplanar arrangement of these carbons, and a C2h symmetry point group. “Anti4” is obtained by having only one synperiplanar arrangement of the external carbons. Its symmetry point group is C1. Anti3 is the least stable conformer due to the unfavourable synperiplanar arrangement of the external carbons. Below are presented Anti2 and gauche3 conformers respectively.
|
Gauche conformers of 1,5-hexadiene were obtained by setting the dihedral angle of the central 4 carbon atoms to 60° conformation, and adjusting the external dihedral angles and bond orientations. Gauche3 is the lowest energy conformation with a total energy about -231.69266 (0.00 kcal/mol) and thereby lower in energy than the corresponding Anti1. Nonetheless such energy difference is largely insignificant considering the barrier to rotation about a single bond. Staggered conformations are expected to be more stable than parent eclipsed ones as the bulky groups are placed further apart resulting in less steric strain. Most of the lowest energy conformers are indeed the anti conformers with the exception of the “Anti 3” and “Anti 4”which are comparatively high in energy and “gauche 3”, which is comparatively low in energy. “Anti 3” and “Anti 4” both have one of the alkene groups pointing out of the molecule central plane leading to steric clashes with hydrogens on the central carbons. The gauche 3 molecule is more probably stable than expected due to favourable σ C-H bonding, π* C=C antibonding orbital overlap. In any case rotation about the central bond is assumed.
Anti2 and Gauche3 conformations were modelled again at a higher level of theory using both a more advanced method namely a density functional one and a more accurate basis set 6-31Gd. Whilst the geometrical differences between the optimised structures are quite minor the differences in total energy are quite significant. The results are presented in the following table. This confirms that higher level of theory methods allow to finetune calculations.
As the Anti2 conformer is considered to be the starting material for the Cope rearangement, a frequency analysis was performed to confirm that the structure is indeed a minimum and to provide thermochemical data for later comparison with experiemental data. The same method and basis set are used as in the last optimisation step. No negative frequency was obtained, suggesting that the optimised structure is a minimum.
|}{|
Vibration |
|}
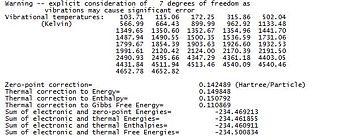
Thermochemical data more precisely vibrational temperatures were recorded from the Gaussian output file at both 278.15K and 0.0001K a presented in the following table. The data at near 0 K was collected by running a second frequency calculation using the opt=readisotope option. The vibrational temperatures described bellow may be used to predict energy changes for a reaction and allow comparison with experiments.
| Value | HF/6-21Gd 298.15K | B3LYP/6-31Gd 298.15K | B3LYP/6-31Gd 0.001K |
|---|---|---|---|
| Total electronic Energy / Hartree | -232.98332 | -234.61170 | -234.468776 |
| Sum of Electronic and Zero-Point Energies / Hartree | -232.830852 | -234.469213 | -234.468776 |
| Sum of Electronic and Thermal Energies / Hartree | -232.8223848 | -234.461855 | -234.468776 |
| Sum of Electronic and Thermal Enthalpies/ Hartree | -232.822903 | -234.460911 | -234.468776 |
| Sum of Electronic and Thermal free energies/ Hartree | -232.862124 | -234.500834 | -234.468776 |
The “sum of electronic and zero-point energies” is the potential energy at 0 K including the zero-point energy (E = Eelec + ZPE). The “sum of electronic and thermal energies” is the energy at 298 K and 1 atm including translational, rotational and vibrational energy modes (E = E + Evib + Erot + Etrans). The “sum of electronic and thermal enthalpies” contains a correction for RT (H = E + RT). The “sum of electronic and thermal free energies” includes the entropic contribution to free energy (G = H - TS).
The energy values at temperatures near 0 (0.001K) method are almost equivalent except for the total energy. Since the temperature is almost zero the values for the “Sum of Electronic and Thermal Energies”, the “Sum of Electronic and Thermal Enthalpies” and the “Sum of Electronic and Thermal Free Energies” is expected to be equal to the “Sum of Electronic and Zero Point Energies”.
Optimisation of the Chair and boat transition structures
The two potential transition states are optimized here using various methods in order to determine which is more likely during the Cope Rearrangement. For the chair transition state two methods are employed here, whereby the first involves an initial computation of the force constant and the second redundant coordinates. The boat transition state is optimized using a QST2 method. In all three cases, the optimization is first carried out at the HF/3-21G level of theory and then at the BLPY3/6-31Gd level of theory. The activation energies of both transition states may be calculated from the frequency outputs allowing to determine which of them of more likely to occur.
Chair transition state
Optimisation via the force constant matrix calculation
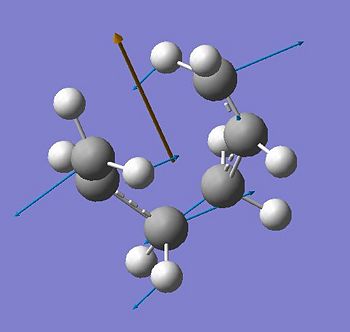
An allyl fragment with an effective 1.5 C-C bond order was drawn in Gaussview and optimised at the HF/3-21G level of theory, in order to build the chair transition state from the optimized fragments. The resulting guess for the chair transition state was then optimized using two different techniques. The first method involves computing the Hessian (force constant matrix) in the first step of the optimization. The structure was optimised to a transition state (Berny) with the additional key words opt=noeigen at the HF/3-21 G level of theory. “NoEigen” prevents the system from crashing should more than one imaginary imaginary frequency be found. This is likely to occur should the guessed transition state structure not be accurate enough. The frequency calculation resulted in one imaginary frequency at -818.08 cm-1, where the vibration corresponds to one end of the fragments move closer to each other, the other moving away. This suggests a concerted bond breaking/bond making mechanism for the Cope rearrangement.
|}{|
Vibration |
|}
Optimisation via the frozen coordinate method
The second method used to optimize the chair transition state was the frozen coordinate method. This involved initially setting the inter-fragment distance between the two reacting terminal carbon pairs to 2.2Å respectively. The first optimization relaxes the rest of the structure with the frozen coordinates mentioned. The inter-fragment distance is then optimized in a second step to yield the transition state. The resulting geometry is very similar to that obtained from the first method and one imaginary frequency at 818cm-1 was obtained. The inter-fragment distances resulting from method one and method two were 2.0206 and 2.0205 respectively suggesting that both methods are consistent. Nonetheless both methods show limitations. Whilst the first method requires a very precise guess of the transition state in question the second method requires the inter-fragment distance between two terminal carbons to be estimated accurately.
Boat transition state
Optimisation via Q2ST method
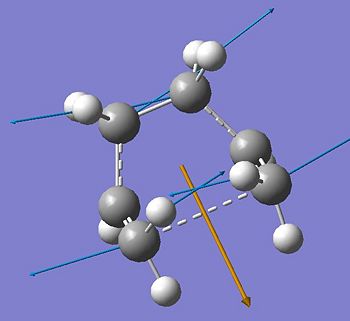
The boat transition structure was optimised using the QST2 method, which involves symmetrizing reactant and product and interpolating between the two structures to guve the transition state. The HF/3-21G optimised anti2 1,5-hexadiene structure was used for both the reactant and product geometries. Crucially, the structures were numbered such that the product numbering corresponded exactly to that of the reactant having undergone a Cope rearrangement. The exact same numbering scheme was used as provided in the tutorial. In order to run a successful optimization to a boat transition state the relative starting geometries had to be altered. The dihedral angle of the central carbons was changed to 0° and both inside C-C-C angles to 100° for both reactant and product. The optimization gave a boat-like transition structure, with an added single bond between one terminal C-C pair. The energy was of -231.60280 Hartree and the imaginary frequency was at -838 cm-1. The interfragment distance between the terminal Carbons is 2.14 Å and the C-C bond length is 1.38 Å. The symmetry point group was C2v.
|}{|
Vibration |
|}
Intrinsic reaction coordinates
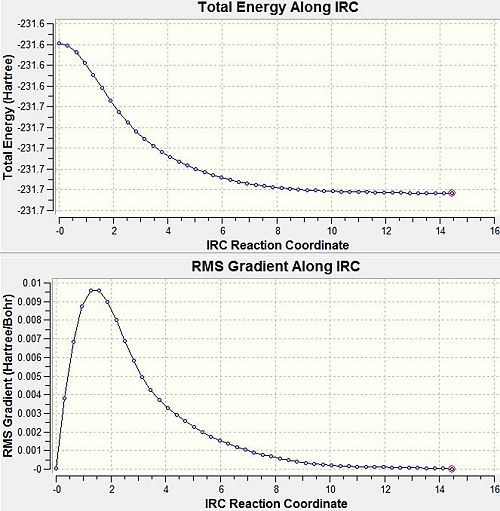
Intrinsic reaction coordinates are used to follow a transition state in along the minimum energy path towards the product for it is almost impossible to predict which product conformer will result from the transition state. An Intrinsic Reaction Coordinate calculation takes a transition state and proceeds in very small geometrical steps in the direction of the steepest slope of the potential energy surface looking for the conformers connecting to the transition state. The IRC is performed using the chair transition state. In this Cope rearrangement the reaction coordinate is symmetrical, the IRC calculation is solely performed in the forward direction. Initially the force constants were calculated once initially and assumed subsequently for all 50points.In order to improve the calculation, a more computationally costly method calculating the force constants at each step was used. In the first case both cases, the global minimum on the potential energy surface was found at the 27th point, in the second case at the 47th point. In fact, the intrinsic reaction coordinate is already terminated when the gradient of the potential energy graph is assumed to be small enough to be considered a minimum. The energy of the resultant product is -231.69166 Hartree and the point group is C2, corresponding to the 'gauche 2' conformer. Tha main steps along the reaction coordinate are presented bellow.
 |
 |
 |
 |
 |
Thermochemical analysis
After having run all optimization at the HF/3-21G level of theory, the chair and boat transition structures were re-optimised at the BL3YP/6-31Gd level to obtain better accuracy estimations of the activation energies. The following table compares thermochemical data of the transition states at different temperatures and different levels of theory. Thermochemical data allows to determine the activation energy of the Cope rearrangement towards the respective transition state. The activation energy corresponds to the difference between the energy of the transition state and the reactant (Anti2). The activation energies are calculated at 0 Kelvin from the sum of the electronic and zero point energies given for both reactant and transition state in the Gaussian output files. The results are summarised bellow for different levels of theory.
| Chair | Chair | Boat | Boat | |
|---|---|---|---|---|
| Value | HF/3-21G | B3LYP/6-31Gd | HF/3-21G | B3LYP/6-31Gd |
| Electronic Energy / Hartree | -231.619 | -234.557 | -231.603 | -234.543 |
| Sum of Electronic and Zero-Point Energies / Hartree | -231.467 | -234.415 | -231.451 | -234.402 |
| Sum of Electronic and Thermal Energies / Hartree | -231.461 | -234.409 | -231.445 | -234.396 |
| Activation energy (Electronic energy TS-Electronic energy reactant) / Hartree | 0.073 | 0.054 | 0.087 | 0.067 |
| Activation energy / kcal/mol | 45.71 | 34.43 | 55.60 | 41.96 |
| Imaginary Frequency / cm-1 | -818 | -566 | -840 | -529 |
Using different basis sets yields strikingly different results for the activation energies. Whilst the lower level of theory only allows to predict that the chair transition state should be more stable than the boat transition state, the density functional method gives quite accurate numerical predictions of the activation energies in both cases. For the chair transition state the activation energy is predicted to be 34.43kcal/mol , which compares quite well with the experimental values of 33.5 (+/-0.5)kcal/mol. Similarly, for the boat transition state computed activation energy, 41.96kcal/mol is reasonably close to the experimental values of 44.7 (+/-2) kcal/mol. Overall then, since the chair transition state has a lower activation energy than the boat transition satet, one may conclude that the Cope rearrangement is more likely to occur via the former rather than the latter transition state.
The Diels Alder cycloaddition
The Diels Alder cycloaddition is a pericyclic reaction involving the formation of two σ sigma bonds between the termini of a diene and a dienophile via a concerted cyclic transition state. The π orbitals of the dieneophile are used to form new σ bonds with the π orbitals of the diene, and the number of π electrons involved determines the stereospecificity of the reaction. There are (4+2) π electrons involved and since the reaction is thermal it proceeds via Hückel topology with only suprafacial components. The new bonds therefore form on the same face of one of the π systems. The Diels-Alder reaction is therefore referred to as a π4s + π2s cycloaddition whereby both bonds are formed at the bottom face of the diene and either at the top face of the dienophile (exo form), or at the bottom face (endoform) of the dienophile. In general, the reaction isunder kinetic control the less theremodynamicaly stable endo isomer is formed preferentially. The regiochemistry of the reaction nonetheless depends on the relative substitution of the double bonds, as substituents that have π orbitals may interact with the new double bond being formed.
The Diels Alder reaction is only allowed and proceeds via a concerted stereospecific fashion when the HOMO of one reactant can interact with the LUMO of the other reactant to form new bonding and antibonding MO’s, which requires them to have the same symmetry. Normal electron demand corresponds to the interaction of the HOMO of an electron rich diene with the LUMO of an electron deficient dienophile. Inverse electron demand involves the reaction between an electron deficient diene and electron rich dienophile. The first part focuses on the prototypical reaction between cis-butadiene and ethane and the orbital interactions involved during the reaction. The regiochemistry of the Diels Alder cycloaddition will be studied in the later part of this exercise at the hand of the reaction between cyclohexadiene with maleic anhydride.
Diels Alder reaction of cis-cyclobutadiene with ethene

Optimisation of cis-cyclobutadiene
Optimisation
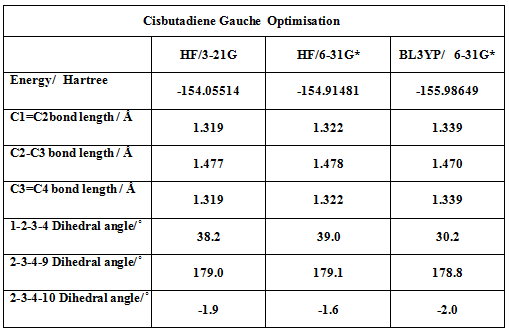
Cisbutadieneoptimisation.JPGCis-Butadiene may either have a gauche-cis or an s-cis conformation, with the former conformation being more stable than the latter one. Cis butadiene was initially modeled in its gauche conformation using quantum mechanical methods and basis sets aof different levels of theory. Bond lengths and bond angles were initially set to values reported by . Nonetheless, for the sake of the Diels alder reaction and the involved orbital interactions, a more plane s-cis conformer is more suitable. The latter conformer was optimized using a semi empirical method at the AM1 level of theory.
Molecular Orbital analysis of cis-cyclobutadiene
| Cis-butadiene HOMO |
Cis-butadiene LUMO |
Ethylene HOMO |
Ethylene LUMO | |
|---|---|---|---|---|
| Molecular Orbital |  |
 |
 |

|
| Symmetry (wrt plane) |
Antisymmetric | Symmetric | Symmetric | Antisymmetric |
 |
 |
The Molecular orbitals were computed in both cases, with the more s-cis orbitals being more symmetric due to the greater planarity. The gauche molecular orbitals are not in fact perfectly symmetric or antisymmetric as suggested by the labels. The HOMO exhibits one node additionally to the nodal plane and is antisymmetric (A) with respect to the plane of symmetry bisecting the central carbon-carbon bond. The LUMO shows 2 nodes additionaly to the nodal plane and is symmetric (S) with respect to the plane of symmetry bisecting the central carbon-carbon bond. In the case of ethene, the HOMO is symmetric with respect to its carbon-carbon bisecting plane of symmetry and the LUMO antisymmetric. As mentioned afore, the HOMO of butadiene may interact with the LUMO of ethene or vice versa due to matching orbital symmetry. Such overlap of electron density means that the reaction is allowed should the signs be match up. The reaction is allowed should orbital signs match up. An orbital correlation diagram would show that it is for instance the HOMO of the butadiene that reacts with the LUMO of ethene.
Optimisation of the enveloppe transition state
In order to optimize the transition state for the Diels alder reaction, 2,2,2-bicyclooctane was initially draw in Gaussiew, a bridging -CH2CH2- fragment removed and and 2 C-C single bonds replace by C=C double bonds. The number of hydrogens was then adjusted such as to have the reactant molecules placed in a suitable way to form a transition state. The transition state was optimized using the non redundant coordinate method at the HF/3-21G level of theory initially, and later at the BLY3P/6-31*level. The interfragment distance between the cis-butadiene and ethene terminal carbon pairs was frozen at 2.2 Angstrongs in a first step of the optimization. This relaxes the overall structure. In the second step of the optimization to a transition state, one differentiates along these coordinates using a normal guess Hessian. The results of the optimization are presented in the following table, and the optimized transition state depicted below.
Despite showing the same single/double bond scheme as in the reactants, the transition state bonds lengths are significantly altered. Indeed, the former “cis-butadiene fragment” shows its double bonds lengthened and its single bond shortened such that they all are about 1.4 Angstrongs long. Furthermore, the resulting interfragment distance of about 2.22 Angstrongs suggests a bond formation process between the two fragments. The Van der Waals radius for a carbon atom being approximately 1.8 Angstrons implies that the non bonded distance between two such atoms would be 3.6 Angstrons. The new σ bonds are forming simultaneously as they have the same length in the transition state implying a synchronous concerted mechanism. The presence of an imaginary at -818cm-1 further confirms the transition state. The former ethene and butadiene fragments moved towards each other in a symmetrical fashion, implying the bond formation between their respective termini. The lowest positive twisting vibration of the ethene molecule with respect to the cis-butadiene fragment which would perhaps suggests a degree asynchronicity of the transition state formation
 |
 |
Geometry and Molecular orbital analysis
The transition state exhibits an "envelope" geometry, which maximises orbital overlap. The ethene fragment approaches from below the plane of the butadiene.Since the transition state only has suprafacial components, both new σ bonds are forming at the bottom face of butadiene and at the top face of the ethene. The Huckel transition state resulting from a thermally allowed Diels Alder reaction state is characterized by a plane of symmetry and aromaticity as it involves 6 cyclically conjugated π electrons. The angle of approach of the ethene component with respect to the butadiene is approximately 111° correlating with a tetrahedral angle of approach (90 °). Whilst the latter angle is expected orbital overlap it would also lead to more steric repulsions. The formally planar ethene hydrogen atoms are also distorted towards a tetrahedral angle the transition state.
HOMO |
LUMO | |
|---|---|---|
| Molecular Orbital |  |

|
| Symmetry (wrt plane) |
Symmetric | Symmetric |
The HOMO and LUMO generated in the transition state are antisymmetric and symmetric respectively. The HOMO is generated from the linear overlap of the LUMO π* orbital of the ethene fragment and the HOMO of the butadiene fragment, both being antisymmetric. The LUMO of the transition state is generated from the HOMO of the ethene fragment and the LUMO of the butadiene fragment, both being symmetric.
The relative energies of the frontier molecular orbitals control the reactivity of the Diels Alder reaction.The smaller the energy gap between the HOMO of butadiene and the LUMO of ethene, the greater orbital overlap and the molecular orbital stabilization, the faster the reaction. Since the Diels alder reaction is mostly under normal electron, the more electron deficient the dienophile and electron rich the diene, the faster the reaction. As a consequence, electron donating substituent on the diene lowering the energy of the HOMO, and electron withdrawing group on the dienophile increasing the energy of LUMO, bring the frontier orbitals closer together and accelerate the reaction.
Diels Alder reaction of with cyclohexadiene maleic anhydride:a study of regioselectivity
The Diels-Alder Reaction of Maleic Anhydride and Cyclohexa-1,3-diene features two possible stereochemical outcomes. Exo and Endo isomers are formed depending on the orientation of the dienophile with reaspect to the diene.
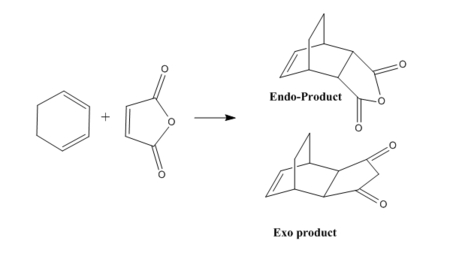
Transition state optimisation
In order to generate the exo and endo transition states, the product structures where first modeled in Chembio3D using a mopac calculation with the PM6 level of theory. The product structures were then imported into Gausview, the inter-fragment bonds removed and hydrogen count adjusted such as to generate a near transition state structure form the starting fragments. Both endo and exo transition states were optimized using a two step redundant coordinate method. In the exo case, the interfragment distances were frozen to 2.2 Angstrongs, and the incoming angle to 111 degrees. In the endo case, freezing the interfragment distances was sufficient to generate a transition state. Both structures were then optimized to a Berny Transition states mentioning the ‘opt=noeigen’ keywords. Both transition states are initially optimized at the HF/3-21G level of theory and thene at the BLY3P/6-21G* level of theory. The results of the optimizations are presented in the following tables.
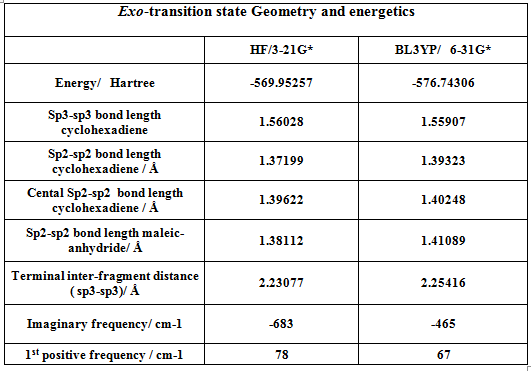
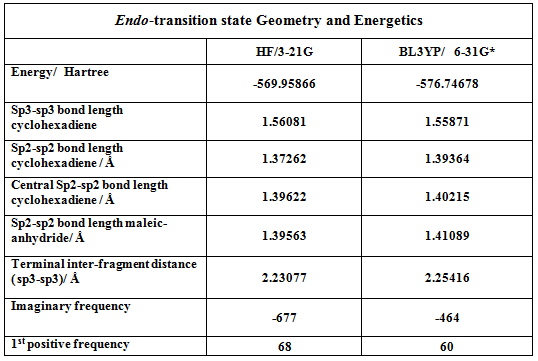
As mentioned afore for the prototypical reaction, the former double bonds and single bonds involved in the reaction are lengthened and shortened respectively and the interfragment distance clearly suggests bond formation. The exo and endo transition states exhibited one imaginary frequency at 465 and 464cm-1 respectively at the BLY3P/6-21G* level of theory. This vibration indeed corresponds to the fragments approaching each other at the appropriate termini.
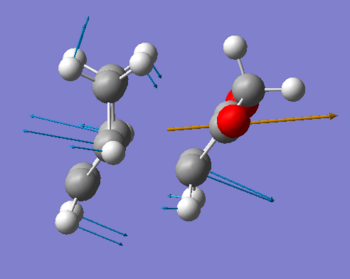 |
 |
 |
 |
Molecular Orbitalanalysis
Reactant substitution leads to regioisomerism in the Diels-Alder reaction. The presence of electron withdrawing oxygens in mealeic anhydride render the C=C strongly electron deficient, and increase the energy of the overlap of the LUMO. The HOMO of the transition state in therefore generated from the LUMO of the maleic anhydride and the HOMO fo the cyclohexadiene which are both antisymmetric. The LUMO of the transition state is generated from the HOMO of maleic anhydride and the LUMO of cyclohexadiene. Since the energy gap between the frontier molecular orbitals is reduced, the reaction is expected to be faster than for the prototypical reaction.
HOMO |
LUMO | |
|---|---|---|
| Molecular Orbital | 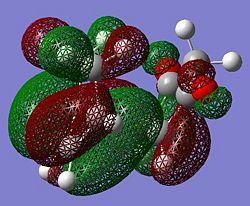 |
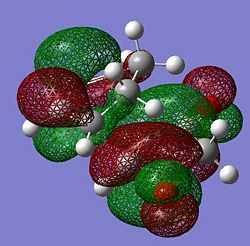
|
| Symmetry (wrt plane) |
Antisymmetric | Antisymmetric |
HOMO |
LUMO | |
|---|---|---|
| Molecular Orbital |  |
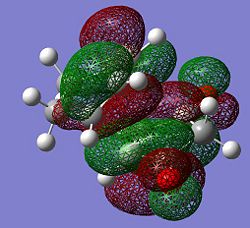
|
| Symmetry (wrt plane) |
Antisymmetric | Antisymmetric |
As may be seen above, the endo transition sate is slightly more stable than the exo transition state, such that under kinetic control the endo product is favoured. Alder suggested that a “plane to plane” orientation of reactants maximising the accumulation of double bonds, which may rationalise the endo selectivity of the reaction. [1] In the endo transition state, the 2 π bonds share the same face whilst in the exo transition state they do not decreasing orbital overlap. The exo transition state is thus comparatively higher in energy. Woodward and Hoffmann proposed that the HOMO-LUMO interactions in the endo transition state were more favourable than in the exo transition state due to orbital symmetry. The endo selectivity is assigned to the secondary overlap.[2] Secondary molecular orbital overlap of the maleic anhydride C(O)-O-C(O) with the C(H)=C(H) is greater in the endo case than in the exo case as the two fragments share the same face and are thus better aligned. It can be seen from the MOs that both the endo and the exo have a nodal plane down the plane symmetry. Furthermore, the endo transition state exhibits a small amount of electron density on the oxygen atom, which is in the same phase as the secondary orbital overlap which leading to further stabilization of the endo transition state. As a conclusion, the Diels Alder reaction of maleic anhydride with cyclohexadiene, is allowed under thermal conditions and is under kinetic control. The endo product is this favoured due to stabilization of the transition state due to better alignment of double bonds and secondary orbital overlap.
Reference
- ↑ K. Alder and G. Stein, Liebigs Ann. Chem., 1933, 504, 210-257.DOI:10.1002/jlac.19335040115
- ↑ The conservation of orbital symmetry.R. Hoffmann, R. B. Woodward Acc. Chem. Res. , 1968 , 1 , 17 - 22DOI:10.1021/ar50001a003