Rep:Mod:3cg507

The Cope Rearrangement

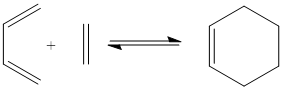
Here we will be using the Cope rearrangement of 1,5-hexadiene to analyse the chemical reactivity. By locating the low energy minima and the higher energy transition state structures of the potential energy surface of this molecule we will predict the reaction mechanism of this reaction. The reaction is an example of a [3,3]-sigmatropic shift, which is an example of a concerted cyclical, pericyclic reaction. It is thought that this reaction goes via a 'chair' or 'boat' transition state with the former being the lowest energy reaction pathway. A Gaussian calculation using a B3LYP method with a 6-31G* basis set has been previously shown to provide results that compare favourably with the experimental values.

Optimising the Reactants and Products

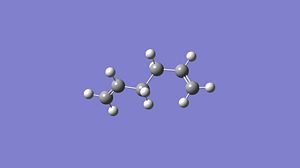
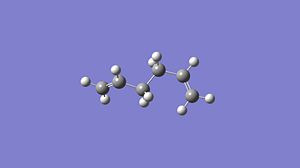
anti 1,5-hexadiene

Firstly a molecule of 1,5-hexadiene with an anti likage of the central four carbon atoms was constructed using Gaussview and Optimised using a Gaussian calculation with a HF/3-21G method and basis set. These structures were then further optimised using a B3LYP/6.31G* method and basis set. The three optimisations I performed found three different 'anti' structures and the optimisation information for each optimisation method can be found below:

Table 1. Optimisation of anti 1,5-Hexadiene
	Optimisation of anti 1,5-Hexadiene
	Anti 1 HF/3-21G	Anti 2 HF/3-21G	Anti 3 HF/3-21G	Anti 1 B3LYP/6-31G*	Anti 2 B3LYP/6-31G*	Anti 3 B3LYP/6-31G*
Point Group	C₁	C_i	C₂	C₁	C_i	C₂
Total Energy A.U.	-231.69	-231.69	-231.69	-233.34	-233.34	-233.34
RMS Gradient Norm A.U.	0.00001285	0.00001891	0.00001296	0.00002336	0.00000537	0.00000612
Dipole Moment D	0.2957	0.0000	0.2021	0.3050	0.0000	0.2095

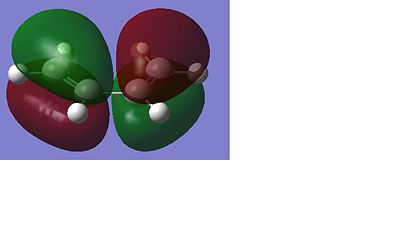
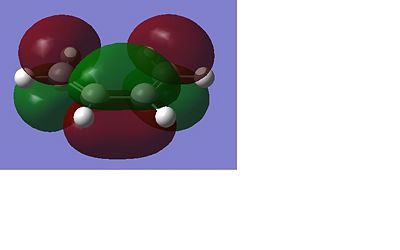
Table 2 shows the optimised structures of the 1,5-hexadiene at the two different levels of theory both in pictorial and in a rotatable jmol format. It can be seen that via both levels of theory the structures with C_i and the C₂ point group symmetry are the structures with the lowest energy, with the C₁ being a higher energy structure. The C_i structure is equivalent to the anti 2 conformer in the appendix of the Module 3 tutorial, the C₂ is equivalent to the anti 1 conformer. The higher energy C₁ conformer is equivalent to the anti 4 conformer. I would expect that the C_i or the C₂ would be the lowest possible conformation of 1,5-hexadiene as in these arrangements there will be no steric factors that affect the stability of the conformer as each part of the molecule can occupy its own space. This is shown below with these conformers being the lowest in energy. The different levels of theory can be shown to have very little effect in the structure of the optimised molecule, this can be seen below as there is very little difference in the structures of the optimised molecules from each level of theory.

Table 2. Optimisation of anti 1,5-Hexadiene
	Optimisation of anti 1,5-Hexadiene
Molecule	Point Group	HF/3-21G	Energy HF/3-21G	B3LYP/6-31G*	Energy B3LYP/6-31G*
anti 1	C₁		-231.691		-233.335
anti 2	C_i		-231.693		-233.336
anti 3	C₂		-231.693		-233.336

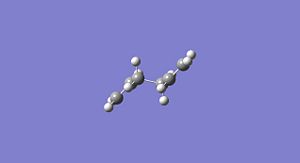
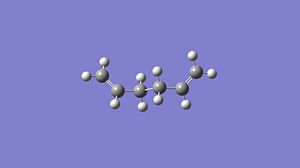
gauche 1,5-hexadiene

Now molecules of 1,5-hexadiene with a gauche relationship between the 4 central carbon atoms was studied and the energy and structures of three of the 6 possible gauche relationship structres are presented below. Again these structures were optimised using two different levels of theory, firstly the HF/3-21G method and basis set and then again with the higher level of theory B3LYP/6-31G* method and basis set. I would expect the gauche conformers of 1,5-hexadiene to be higher in energy than the anti linked conformers due to the steric repulsion of the two terminal CH₂ groups. A repulsion not present in the anti linked conformer.

Table 3. Optimisation of gauche 1,5-Hexadiene
	Optimisation of gauche 1,5-Hexadiene
	Gauche 1 HF/3-21G	Gauche 2 HF/3-21G	Gauche 3 HF/3-21G	Gauche 1 B3LYP/6-31G*	Gauche 2 B3LYP/6-31G*
Point Group	C₂	C₁	C₁	C₂	C₁
Total Energy A.U.	-231.69	-231.69	-231.69	-233.33	-233.33
RMS Gradient Norm A.U.	0.00001037	0.00001737	0.00000532	0.00001575	0.00000537
Dipole Moment D	0.4554	0.5360	0.2021	0.3407	0.5704

Table 4. Optimisation of gauche 1,5-Hexadiene
	Optimisation of gauche 1,5-Hexadiene
Molecule	Point Group	HF/3-21G	Energy HF/3-21G	B3LYP/6-31G*	Energy B3LYP/6-31G*
gauche 1	C₂		-231.688		-233.332
gauche 2	C₁		-231.689		-233.333
gauche 3	C₁		-231.693		-231.693

Frequency Analysis

Using the B3LYP/6-31G* optimised structure with the C_i point group symmetry a frequency analysis was performed. Through this analysis it is possible to confirm that the structure is at a minimum in energy along the potential surface of the molecule, this is the case as all of the vibrational frequencies of the conformer are positive and hence real frequencies. It is also necessary to perform this analysis to enable us to compare the energies of this molecule to experimentally determined values, the frequency analysis provides the energy of the system with some additional terms included to allow this comparison to be made. Looking at the thermochemistry data provided in the checkpoint file of the Gaussian frequency calculation the following energies can be found:

Sum of electronic and zero-point Energies= -233.192872 A.U. This adjustment of the energy of the conformer shows the potential energy at 0K including the zero-point vibrational energy (E=E_elec+ZPE).

Sum of electronic and thermal Energies= -233.185569 A.U. This shows the energy at 298.15K at 1atm which includes translational, rotational and vibrational energy nodes at this temperature (E=E+E_vib+E_rot+E_trans).

Sum of electronic and thermal Enthalpies= -233.184625 A.U. This contains the entropic contribution to the free energy (G=H-TS)

Sum of electronic and thermal Free Energies= -233.224534 A.U. This shows an additional correction for RT (H=E+RT) which is important in dissociation reactions

Optimising the 'Chair' and 'Boat' Transition Structures

Now the optimisation of the transition state structure will be performed using three different methods firstly by calculating the force constants at the beginning of the calculation, the via a redundant coordinate method and finally by a QST2 method. The Intrinsic Reaction Coordinate and the activation energies for the two different transition state structures ('Chair' and 'Boat') will then be calculated. These transition structures constsist of two CH₂CHCH₂ fragments positioned at about 2.2Å apart one with C_2v and one with C_2h symmetry.

Chair

Chair Conformation

Firstly the CH₂CHCH₂ fragment was constructed using Gaussview, it was then optimised using a HF/3-21 method and basis set and the energies and structure can be seen below.

Table. 5 Optimisation of the CH₂CHCH₂ fragment
	Fragment
Total Energy A.U.	-115.75
RMS Gradient Norm	0.00013184
Dipole Moment D	0.0081
Point Group	C_2v

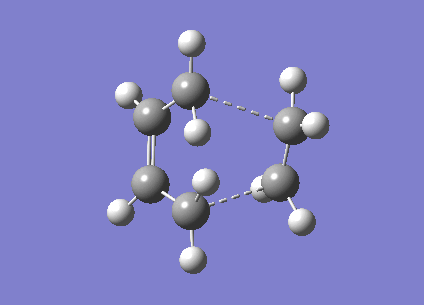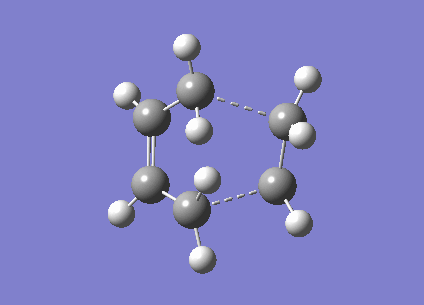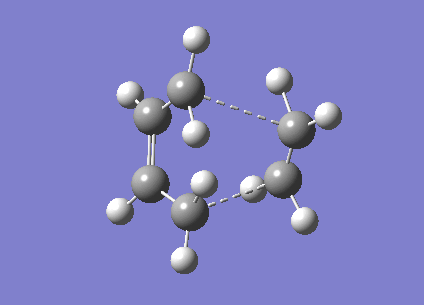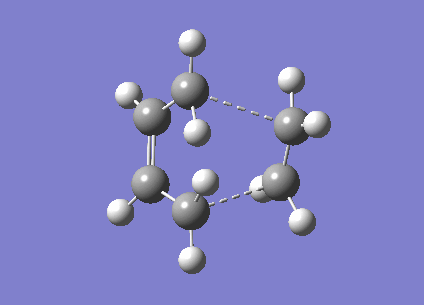
For a transition state geometry optimisation the calculation needs to know where the reaction coordinate is, as we know what the transition state should look like we can guess the geometry. The easiest optimisation then computes the force constant matrix or Hessian in the first step and then updates this throughout the optimisation, this is the method used for the first optimisation of the 'chair' transition state. This optimisation used a HF/3-21 method and basis set and the energies and structure of the optimised transition state can be seen below. This method optimised the structure to a TS (Berny) structure and the command Opt=NoEigen is included to allow multiple imaginary frequencies to be calculated. The imaginary frequency of this transition state is -817.9cm^-1 which corresponds to the cope rearrangement and can be seen below.

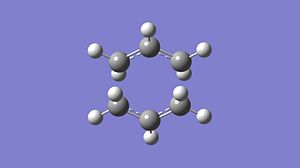
Table. 6 Optimisation of the guess of the Chair Transition state conformer
Total Energy A.U.	-231.62
RMS Gradient Norm	0.00001580
Dipole Moment D	0.0004

Frozen Coordinate Method

The next method used to optimise the transition state structure was a frozen coordinate method. Using the Redundant Coordinate Editor in Gaussview the terminal carbons involved in the bond formation or bond breaking were frozen to one position 2.2 Å apart. The optimisation was then carried out as if the optimisation were to a minimum using a HF/3-21G method as basis set. Once the first optimisation was carried out the resulting structure is very similar to the chair transition state calculated by the previous method, however here the distance between the terminal carbons involved with the bond breaking and formation have a fixed distance of 2.2 Å. Taking the checkpoint file of the optimised structure with the fixed bond distances, the structure was then optimised again to find the optimised transition structure without the fixed distance between the terminal carbons. A transition state optimisation was used but the force constants are not calculated instead a normal guess Hessian is included which is modified to include the coordinates of the two bonds we are differentiating along.

Chair Transition State from frozen coordinate optimisation

Table. 7 Optimisation of the Chair Transition state conformer by the frozen coordinate method
	Fragment
Total Energy A.U.	-231.62
RMS Gradient Norm	0.00005582
Dipole Moment D	0.0000
Point Group	C₁

The bond forming/breaking length obtained from this structure was found to be 2.01875Å, lower than the fixed bond length imposed in the first step. The transition state structure obtained from this method has a very similar structure to the transition state structure obtained in the first method.

Boat

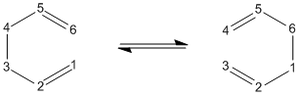
Now the 'Boat' transition state structure will be optimised using a QST2 method, in this method the reactant and product molecule is specified and the transition state structure is found by interpolating between the two structures. It is important that the atoms in the structures are labelled in exactly the same way for both the reactant and the product to allow the method to work properly, as shown in the Cope rearrangement diagram above. The product and reactant structure was taken from checkpoint file of the C_i point group symmetry anti linked 1,5-hexadiene by copying the structure and pasting it to new molgroup window. Then another molecule was pasted in using the add to molgroup function which provides two windows with what will be the reactant and product of the reaction.

Boat Conformation

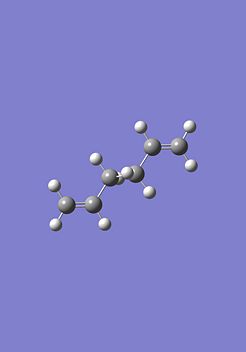The reactant and product as seen above were numbered correctly by editing the atom list in the Gaussview edit menu. The system was then optimised to a QST2 using a HF/3-21G method and basis set. As the starting product geometry was set as above the method failed, a linear interpolation failed to locate a 'Boat' transition structure. To ensure that the method could find the 'Boat' transition state structure the reactant and product molecule geometries were modified. The central C2-C3-C4-C5 dihedral angle was changed from 180 to 0 degrees and the C2-C3-C4 and C3-C4-C5 were reduced from about 111 to 100 degrees. The final geometries can be seen below, they are show the strict numbering system required to perform the QST2 optimisation.

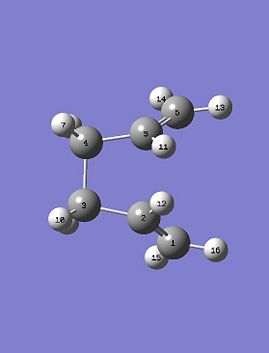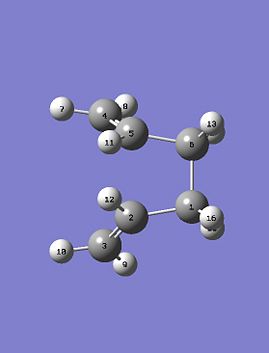Boat Transition State from QST2 optimisation

Table. 8 Optimisation of the Boat Transition state conformer
	Fragment
Total Energy A.U.	-231.60
RMS Gradient Norm	0.00003462
Dipole Moment D	0.1584

This is a good method as it finds the transition state from the reactant and product without the need to used optimised fragments and adjusting the position and orientation of the fragments. However as we discovered if the geometry of the reactant and product is not not similar to the transition state geometry then the QST2 optimisation will fail.

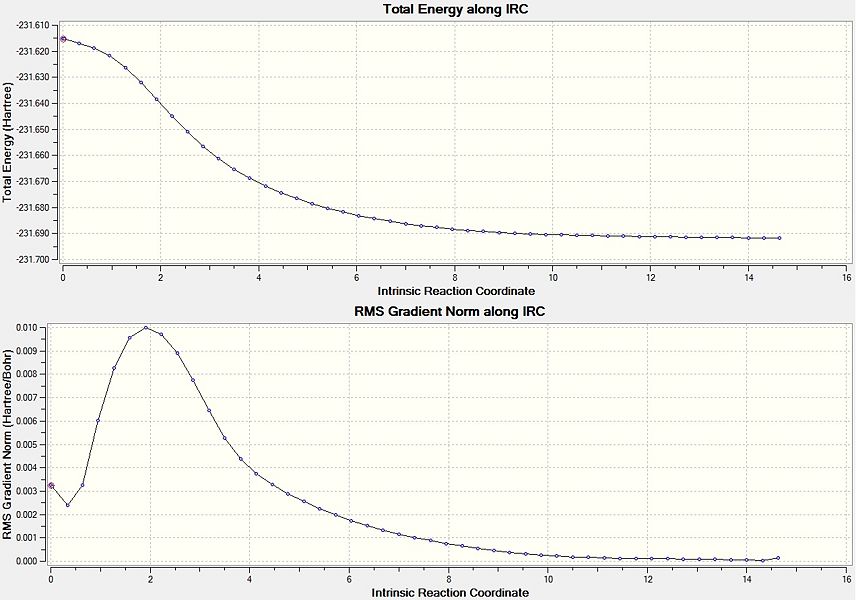
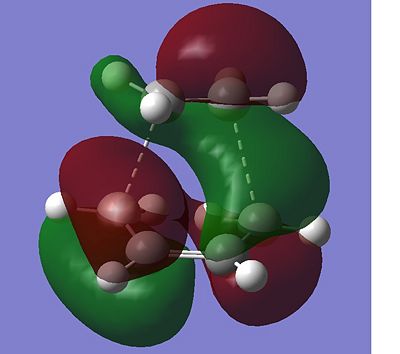
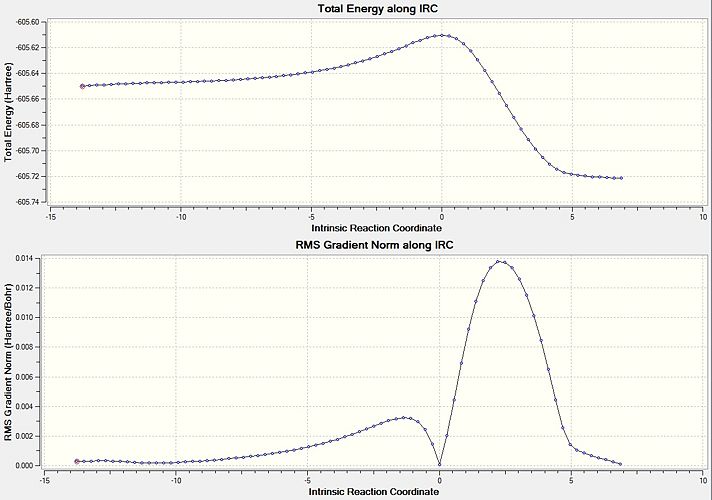
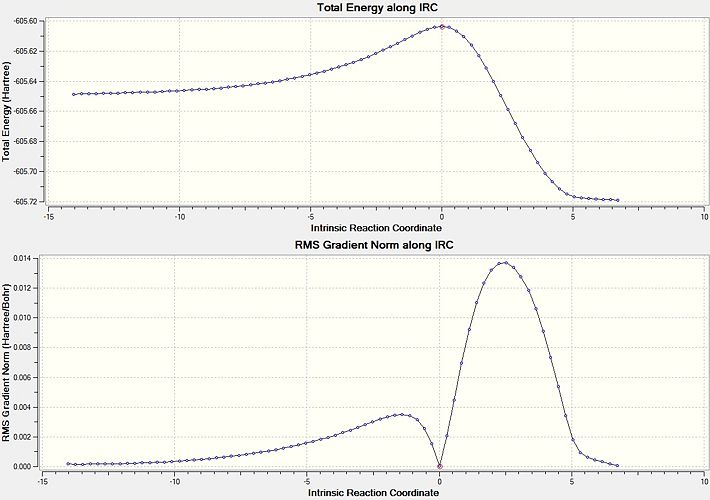
Intrinsic Reaction Coordinate of Chair conformer

From the transition state structures it would appear that a gauche product would be formed via a "Boat' transition state and an anti product would be formed via a 'Chair' transition state. A better way to investigate the problem regarding how a transition state proceeds to give a particular geometry is to calculate the Intrinsic Reaction Coordinate (IRC). This shows the minimum energy reaction path from the transition state structure to the local minima. This invloves small changes to the structure of the molecule where the gradient of the energy surface is at its steepest.

Taking an optimised geometry of the chair transition state an IRC calculation is performed, as the reaction coordinate will be symmetrical it was only run in one direction. To ensure that the calculation is successful, 50 steps along the reaction coordinate were calculated with the force constants calculated at each step. The results of this calculation are shown below.

Chair Transition State at maximum energy on the IRC curve

B3LYP Optimisation and Frequency Analysis

A calculation of the activation energies of the reaction via both transition structures can be carried out by optimising the 'Chair' and 'Boat' transition structures again using the B3LYP/6-31* method and basis set and then carrying out a frequency calculation. In the calculations carried out the B3LYP/6-31* method failed to find the optimised structure and hence the final energies provided will not be the lowest energy of the molecule, giving activation energies as shown below that are close to experimental values for the 'Boat' structure but a value for the 'Chair' structure which is significantly different from the experimental values.

Table 9. Optimisation of anti 2 1,5-Hexadiene
	Activations of anti 2 1,5-Hexadiene
	Anti 2	Chair	Boat
Total Electronic Energy B3LYP/6-11G*	-231.69	-233.27	-233.27
Total Electronic Energy and zero-point energies B3LYP/6-11G*	-233.19	-233.06	-233.13
ΔE (kcal/mol) B3LYP/6-11G*	0	81.6	37.7

The conversion factor between Hartrees and kcal/mol - multiply Hartree value by 627.5095. ΔE is calculated by subtracting the electronic energy and zero point energies of the anti 2 from the electronic energy and zero point energies of the transition state structure. The data taken from the log file can be seen below.

Chair Frequency B3YLP

Zero-point correction= 0.142233 (Hartree/Particle)

Thermal correction to Energy=                    0.149035
Thermal correction to Enthalpy=                  0.149979
Thermal correction to Gibbs Free Energy=         0.110952
Sum of electronic and zero-point Energies=           -233.057291
Sum of electronic and thermal Energies=              -233.050490
Sum of electronic and thermal Enthalpies=            -233.049545
Sum of electronic and thermal Free Energies=         -233.088572

Chair

Zero-point correction=                           0.151378 (Hartree/Particle)
Thermal correction to Energy=                    0.157018
Thermal correction to Enthalpy=                  0.157962
Thermal correction to Gibbs Free Energy=         0.122592
Sum of electronic and zero-point Energies=           -231.463808
Sum of electronic and thermal Energies=              -231.458167
Sum of electronic and thermal Enthalpies=            -231.457223
Sum of electronic and thermal Free Energies=         -231.492593

Boat Frequency B3YLP

Zero-point correction=                           0.143316 (Hartree/Particle)
Thermal correction to Energy=                    0.149035
Thermal correction to Enthalpy=                  0.149979
Thermal correction to Gibbs Free Energy=         0.115298
Sum of electronic and zero-point Energies=           -233.130999
Sum of electronic and thermal Energies=              -233.125280
Sum of electronic and thermal Enthalpies=            -233.124336
Sum of electronic and thermal Free Energies=         -233.159016

Boat

Zero-point correction=                           0.151876 (Hartree/Particle)
Thermal correction to Energy=                    0.157505
Thermal correction to Enthalpy=                  0.158450
Thermal correction to Gibbs Free Energy=         0.123684
Sum of electronic and zero-point Energies=           -231.450927
Sum of electronic and thermal Energies=              -231.445297
Sum of electronic and thermal Enthalpies=            -231.444353
Sum of electronic and thermal Free Energies=         -231.479119

Experimental activation energies:

33.5 +/-0.5 kcal/mol chair 44.7 +/-2.0 kcal/mol boat

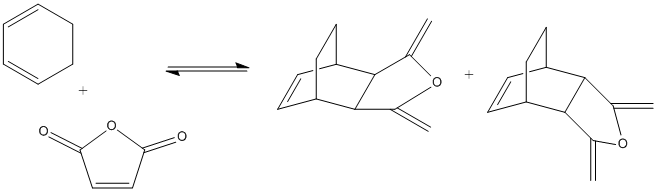
The Diels Alder Cycloaddition

The Diels Alder reaction is an example of a pericyclic reaction, where π orbitals of the dienophile are used to create new σ bonds with the π bonds of a diene. For an allowed concerted pericylic reaction to occur the HOMO of one reactant must interact with the LUMO of another reactant. HOMO/LUMO interactions can only occur if there is a significant overlap of the orbitals. If the dienophile has subsituents containing π orbitals then a stabilisation can occur between these and the π orbitals of the newly formed double bond of the product molecule these are know as secondary orbital overlap effects.

Butadiene and Ethylene

Firsly a simple example involving the Diels Alder [4s+2s] cycloaddition of ethylene to butadiene, where the ethylene approaches the cis butadiene from above.

The butadiene molecule was optimised using the semi-empirical molecular orbital method AM1 and the results of the calculation and the molecular orbitals can be seen below.

Table 10. Molecular Orbitals of cis Butadiene
	Molecular Orbitals of cis Butadiene
Molecule	Molecular Orbital	HF/3-21G Energy A.U.	Symmetric with respect to plane
HOMO		-0.34381	NO (a)
LUMO		0.01707	Yes (s)

The transition state is know to have an envelope type structure which maximises the overlap between the π orbitals. This structure was drawn in Gaussview and then optimised using a HF/3-21G method and basis set.

Table. 11 Optimisation of the Transition state
Total Energy A.U.	-231.515

The Imaginary Vibration is -785.49cm^-1 and this shows the Diels Alder cycloaddition, this reaction shows that the formation of the two new σ bonds is in a synchronised fashion.

Table 12. Molecular Orbitals of Transition State
	Molecular Orbitals the Transition State
Molecule	Molecular Orbital	HF/3-21G Energy A.U.	Symmetric with respect to plane
HOMO		-0.29480	NO (a)
LUMO		0.13342	Yes (s)

Cyclohexa-1,3-diene and Maleic anhydride

Cyclohexa-1,3-diene and Maleic anhydride readily react to provide the products as shown below. The endo product is favoured and as the reaction is kinetically driven the transition state of the exo product is expected to be higher in energy.

Endo Transition State

The cyclohexa-1,3-diene and the maleic anhydride were optimised using a HF/3-21 method and basis set and then the two molecules were placed in the endo shaped orientation with the distance between the carbons involved in the bond forming and breaking set to 1.8Å apart. A transition state (Berny) optimisation was then performed using a HF/3-21 method and basis set and the energies and structure can be seen below.

Table. 13 Optimisation of the endo transition state
	Fragment
Total Energy A.U.	-605.610
RMS Gradient Norm	0.00007360
Dipole Moment D	6.7170
Point Group	C₁

An imaginary frequency was found at -644.91cm^-1 which corresponds to the Diels Alder cycloaddition. The thermochemistry information from the frequency analysis is shown below.

Zero-point correction=                           0.195449 (Hartree/Particle)
Thermal correction to Energy=                    0.204878
Thermal correction to Enthalpy=                  0.205823
Thermal correction to Gibbs Free Energy=         0.160218
Sum of electronic and zero-point Energies=           -605.414916
Sum of electronic and thermal Energies=              -605.405487
Sum of electronic and thermal Enthalpies=            -605.404542
Sum of electronic and thermal Free Energies=         -605.450147

Optimised endo Transition State vibrations

Optimised endo Transition State Bond Lengths

Table 3. Molecular Orbitals of endo Transition State
	Molecular Orbitals the endo Transition State
Molecule	Molecular Orbital	HF/3-21G Energy A.U.	Symmetric with respect to plane
HOMO		-0.32442	NO (a)
LUMO		0.07337	NO (a)

endo Transition State at maximum energy on the IRC curve

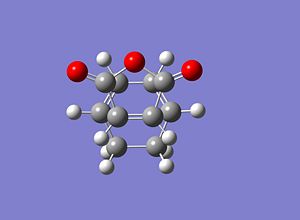
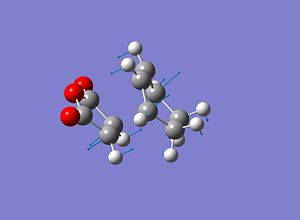
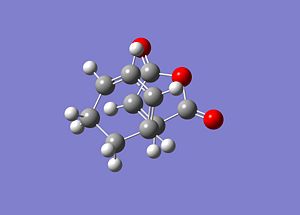
Exo Transition State

The cyclohexa-1,3-diene and the maleic anhydride were optimised using a HF/3-21 method and basis set and then the two molecules were placed in the exo shaped orientation with the distance between the carbons involved in the bond forming and breaking set to 1.8Å apart. A transition state (Berny) optimisation was then performed using a HF/3-21 method and basis set and the energies and structure can be seen below.

Table. 15 Optimisation of the exo transition state
	Fragment
Total Energy A.U.	-605.604
RMS Gradient Norm	0.00002903
Dipole Moment D	5.9344
Point Group	C₁

An Imaginary Frequency of -647.40cm^-1 was found which corresponds to the Diels Alder Cycloaddition. The thermochemistry information from the frequency analysis of the transition state can be found below.

Zero-point correction=                           0.195454 (Hartree/Particle)
Thermal correction to Energy=                    0.204912
Thermal correction to Enthalpy=                  0.205856
Thermal correction to Gibbs Free Energy=         0.159910
Sum of electronic and zero-point Energies=           -605.408137
Sum of electronic and thermal Energies=              -605.398679
Sum of electronic and thermal Enthalpies=            -605.397734
Sum of electronic and thermal Free Energies=         -605.443681

Optimised exo Transition State vibrations

Optimised exo Transition State Bond Lengths

Table 16. Molecular Orbitals of exo Transition State
	Molecular Orbitals the exo Transition State
Molecule	Molecular Orbital	HF/3-21G Energy A.U.	Symmetric with respect to plane
HOMO		-0.32323	NO (a)
LUMO		0.05805	NO (a)

exo Transition State at maximum energy on the IRC curve

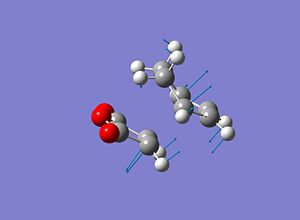
Typical Bond lengths^[1]DOI:10.1088/0022-3719/19/24/006 :

sp³C-sp³C = 1.54

sp³C-sp²C = 1.51

sp²C-sp²C = 1.35-1.48

Carbon Van der Waals Radius^[2] DOI:10.1021/j100785a001 = 170pm

Discussion and Conclusions

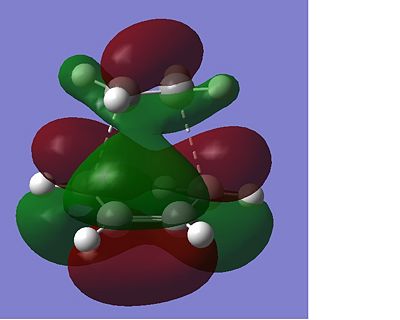
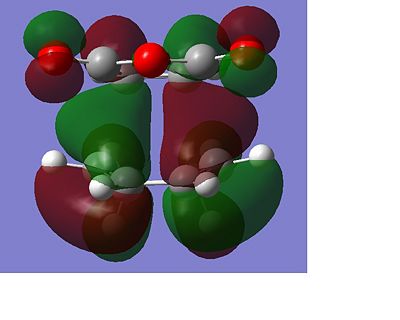
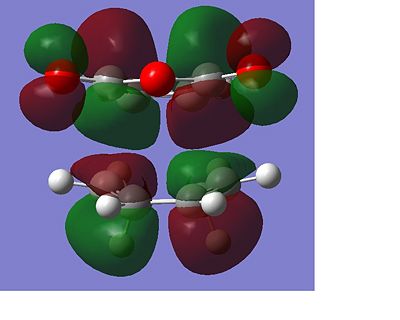
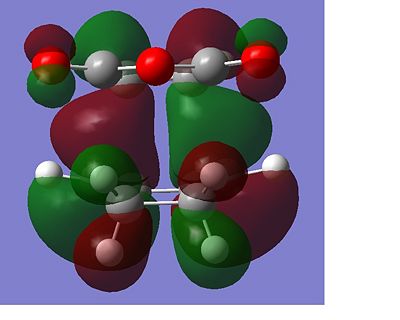
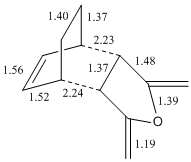
The total energy of the different transitions states shows that the endo product has the lowest energy transition state, -605.610 A.U and the exo product, -605.604 A.U. has the higest energy transition state as predicted. This is also shown in the frequency analysis as the exo product has a higher transition state vibrational energy, 647.40cm^-1, than then endo transition state, 644.91cm^-1. As the endo product is the favoured product, this data supports the assumption that the reaction proceeds under kinetic control. The rotatable jmol structures show that the endo product also has shorter distances between the carbons that form or break the bond at 2.23-2.24Å. While the bond in the exo structure is longer at 2.26Å, this also supports the previous conclusion showing that the two σ bonds that form and break in the exo transition state are weaker as they are longer and they have already been shown to have a higher imaginary vibration and energy. The IRC also shows that the transition states do go on to form the desired product at the following minima. The molecular orbital diagram shows that the HOMO of the endo transition state has a favourable overlap of orbitals between the maleic anhydride and the cyclohexa-1,3-diene which is not present in the exo transition state, this would be a contribution to the lowering of the energy of the endo transition state. There is also a steric clash that can be seen in the exo transition state between the oxygens from the maleic anhydride and the bridging CH₂ groups of the transition state from the cyclohexa-1,3-diene, which would increase the energy of the exo transition state.