Rep:Mod:3boro
Module 1 Organic Computational Lab
Modelling Using Molecular Mechanics
The Hydrogenation of the Cyclopentadiene Dimer
The energies of the endo and exo form of the cyclopentadiene dimer were calculated using the MM2 minimising function on ChemBio3D. The exo dimer has energy 31.8780 kcal/mol and the endo dimer has energy 34.0153 kcal/mol. The lower energy found in the exo dimer is mostly due to less strain (ΔEstrain = 1.8491 kcal/mol) between cyclopentadiene rings. However, the favoured product of cyclopentadiene dimerisation is the endo product due to favourable secondary orbital interactions which molecular mechanics cannot calculate. The dimerisation of cyclopentadiene occurs thermodynamically and the hydrogenation of endo product 2 occurs kinetically.
Table showing Energies of the two hydrogenation products of the endo dimer
| Product 1 | Product 2 | |
| Stretch contributions kcal/mol | 1.2266 | 1.0963 |
| Bending contributions kcal/mol | 18.8517 | 14.5074 |
| Stretch-Bend contributions kcal/mol | -0.7589 | -0.5493 |
| Torsion contributions kcal/mol | 12.2412 | 12.4972 |
| Non-1.4 VDW contributions kcal/mol | -1.5484 | -1.0507 |
| 1,4 VDW contributions kcal/mol | 5.7571 | 4.5124 |
| Dipole/dipole contributions kcal/mol | 0.1630 | 0.1407 |
| Total Energy kcal/mol | 35.9323 | 31.1540 |
|
|
Obviously we can see that product 2 is to be the more likely product because it has an overall lower energy. The contribution that causes product 2 to have lower energy is the significant lowering of the bending energy. This is due to the rigidity of the bridging carbon and double bond which means the molecule is more stable. If the other double bond is hydrogenated then there would be more bending of the rings, thus increasing energy. The same increased rigidity of product 2 explains the lower torsion energy contribution. The 1,4 VDW contributions are lower when the 5-membered ring retains it's double bond becuase the replusion between the bridging carbon and the sigma bond is less than the replusion between the bridging carbon and the pi-bond.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
The Methylation of an Optically Active Derivative of Prolinol using Grignard reageant
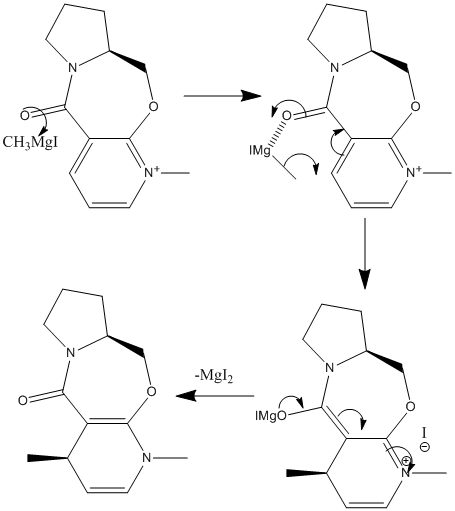
The addition of methyl and amino groups to a pyridinium group was studied using molecular mechanics. Firstly, the reaction of an optically active derivative of prolinol (MM2: 26.3183kcal/mol) with MeMgI was studied (mechanism shown left). Why did the resulting 4-substituted product (MM2: 28.82 kcal/mol) have 'up' stereochemistry?
From studying the orientation of the carbonyl group to the pyridinium ring, it was noted that the amide carbonyl was situated just above the face of the pyridinium ring (angle ≈+10°). This meant that if the Grignard reageant coordinated to the carbonyl, the methyl could be delivered to the upper face of the ring, thus giving the stereochemistry shown in the actual product. The addition of MgMeI to the MM2 was attempted but was not succesful. Instead, Me+ was added to the MM2 calculation: as the structure's energy was minimised the Me+ moved away from the pyridinium to reduce repulsion between the two molecules (MM2: 41.72kcal/mol). It must be noted that another lesser isomer is formed in the addition of a methyl where there is attack of the Grignard reageant at the 2 position on the same ring. The isomeric mixture has the ratio 15:1. [1] Attack at the 2 position is not favoured due to steric hinderance with the methyl on the nitrogen and therefore the 2-substituted product has a higher energy overall (MM2: 29.42kcal/mol).
The Addition of Aniline to an NAD+ analogue
Similarly to the above reaction, the second investigation was to find out why the addition of aniline to a different pyridinium ring also gave the 'up' stereoisomer. The reactant has applications to the atropenantioselective amidification of aryl esters. [2] From looking at the 3D structure of the reactant (below; jmol file) we can see that the conformation of the 7-membered ring allows the carbonyl to be positioned directly 'in the middle' of the pyridinium ring from looking at the molecule from the top face. Thus, the amide carbonyl again shows steric control over the reaction, but in a different way from the above example. The carbonyl is responsible for the high stereoselectivity of the 1,4 reduction because it repels the aniline so it can't react on the bottom face.
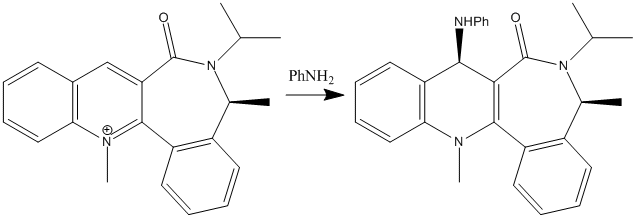
The reactant we are looking at has one atropisomer. An atropisomer is an isomer brought about by steric hinderance of a bond so other conformations cannot be reached. [3] There is an energy barrier of ΔE = 5.812 kcal/mol between the two atropisomers. The isomer we are not studying presents the amide carbonyl above the pyridinium ring: the opposite to the studied isomer. The two atropisomers are also atropenantiomers - the hydrogen next to the carbonyl on the pyridinium ring have different stereochemistry in each isomer meaning they are enantiomers of each other, separated by rotation constraint in the 7-membered ring.
NAD+ |
Further Improvements to the model
In order to further study this reaction we could look at how the solvent coordinates to the reactants and aids or hinders rotation of the σ bonds.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
The two atropenantiomers shown left are intermediates in the synthesis of Taxol, an anti-cancer drug. They are synthesised by the oxy-Cope rearrangement [4]
of the reactant shown above and therefore can only isomerise via this mechanism, not via ring flipping, due to the steric hinderance of the ring flip. The energies were obtained by MM2 calculations. Product 10 is the twist boat conformation of the 10-membered ring (MM2: 54.4966 kcal/mol) and product 11 is the chair conformation of the 10 membered ring (MM2: 47.1795 kcal/mol). The subsequent functionalisation occurs at the alkene. It is observed that the functionalisation occurs abnormally slowly: this is due to the hyperstability of the olefin. [5] Hyperstability refers to the fact that the alkene is less strained than the subsequent alkane. For molecule 11 compared to the hydrogenated product, ΔEstrain = 3.4871 kcal/mol, showing that strain is increased. From looking at the 3D molecule, the functionalisation has caused the hydrogen to be in the middle of the ring (see Jmol below).
Taxol 11 hydrogenated |
The Induction of Peptide Hydrolysis at 298K
In this study we will see how alterating the conformation of a peptide can reduce the half life from 500 years to 20 minutes. The two molecules to be studied are shown below. Two isomers were found for each by varying the N-substituent on the decalin ring so it was axial or equatorial. This required a lot of fiddling of lone pairs and hydrogens because the ring tended to flip back to the most energietically favourable configuration (i.e. equatorial).
| Molecule 13(4aα,8β,8aα)-1-ethylamido-8-hydroxydecahydroquinoline (N subst. equatorial) | Molecule 13(4aα,8β,8aα)-1-ethylamido-8-hydroxydecahydroquinoline (N subst. axial) | Molecule 14(4aα,8α,8aβ)-1-ethylamido-8-hydroxydecahydroquinoline (N subst. equatorial) | Molecule 14(4aα,8α,8aβ)-1-ethylamido-8-hydroxydecahydroquinoline (N subst. axial) | ||||||||||||
|
|
|
| ||||||||||||
| MM2: 19.1 kcal/mol | MM2: 22.2 kcal/mol | MM2: 12.0 kcal/mol | MM2: 17.6 kcal/mol |
The molecular mechanics measurements of each isomer shows that the equatorial positon is preferred. In molecule 13, the difference between Eq/ax was 3.1 kcal/mol. For molecule 14 the difference in isomeric energy was 5.6kcal/mol. The half life for the hydrolysis of the peptide bond in molecule 13 is 21 minutes. The equatorial isomer easily converts to the cyclic ester because the hydroxyl lone pain is at the right position for attack onto the carboxyl carbon. This is due to hydrogen bonding that is able to take place between the hydroxyl group and the nitrogen in the decalin ring thus moving the reactive centres closer together. From looking at the 3D models of molecule 14, it is clear that the equatorial positioned N-substituent does not lend the hydroxyl group easy attack. Therefore the equatorial isomer has to convert to the axial isomer, in which the hydroxyl group is at the correct position to attack (see Hydrogen Bond reference previously). This conversion to the more energetic axial isomer has an energy cost, therefore the halflife for the hydrolysis is a hefty 831 minutes! [6] [7]
So why do these peptides take so much less that 500 years to hydrolyse? The answer lies within the conformation of the molecule. If the hydroxy and carboxyl centre were not at such close proximity to form a 5-membered ring then the hydrolysis would not take place. In nature we require enzymes to help peptides reach the correct conformation to hydrolyse in a reasonable timeframe.
Modelling using Semi-Empirical Molecular orbital theory
Regioselective Addition of Dichlorocarbene
The regioselectivity of the reaction of a diene with dichlorocarbene was considered using molecular mechanics and MO theory. The attack will occur on the opposite face to that containing the cyclopropyl ring,[8] but which alkene is most nucleophilic?
Molecular Surfaces of the Diene
|
The diene shown left was minimised via MM2: 17.8973 kcal/mol. The geometry and energy was then minimised using a Hartree-Fock STO-3G method (Energy: -548182.95 kcal/mol) and the molecular surfaces were determined: the HOMO-1, LUMO, LUMO+1 and LUMO+2 are shown below. The HF/STO-3G self-consistent-field MO method provides an approximation to the electron wavefunction of the molecule so we can see which is the most reactive towards electrophiles. |
We can see a very sizable difference between the energies calculated classically and quantum mechanically. The MM2 method takes into accound repulsion from atoms, dipoles and strain of bonds away from their preffered configuation. However, this method fails to recognise electrons at all - what about repulsion and attraction between molecular orbitals; where are the molecular orbitals? In order to calculate the minimum energy including electrons, quantum mechanical methods must be implemented because classical mechanics is inaccurate for such small, wave-like particles. The Hartree-Fock method is able to calculate wavefunctions and weighting coefficients so we know how big each orbital is, thus being able to judge the magnitude of destabilisation/stabilisation.
|
|
|
|
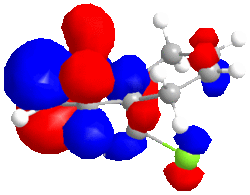
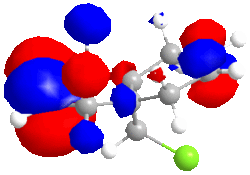
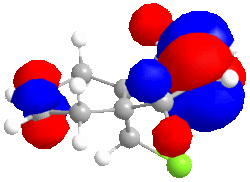
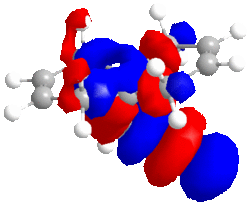
| HOMO -1; -8.447eV | LUMO; 1.675eV | LUMO+1; 8.572eV | LUMO+2; 15.205eV |
The large C-Cl σ* orbital shown in the LUMO-2 orbital should stabilise the endo C=C π* orbital (shown in HOMO-1) but instead, due to opposite phase MOs, there is strong dstablisation between the two MOs perhaps pointing to the endo double bond being attacked to relieve the large destabilisation effects.
The LUMO has nearly symmetrical molecular surfaces so there is equal possibility of attack into each C=C π* orbital, which does not solve our regioselectivity question. The endo C=C π*orbtial is slightly larger than the exo. The LUMO+1 is similar to the LUMO but there is no symmetry. π* orbitals are present but the exo has a larger wavefunction. In the HOMO wavefunction, we can see the Cl pz is in a position to destabilise the exo C=C π* orbital but the destabilisation is not as great as the destabilisation of the endo C=Cπ* by the C-Cl σ* orbital.
In conclusion, I believe the endo-product is observed because the energy gain from the loss of destabilisation between C-Clσ* and the endo C=Cπ* is favourable. This is in agreement with literature. [9]
The Molecular Vibrations of the Diene and Monohydrated Species
The molecular vibrations of diene and the monohydrated species were found using the B3LYP/6-31G(d) method:
| Diene | Monohydrated diene | |
| C=C vibrations | 1740.76 cm-1, 1760.91 -1 | 1761.69 -1 |
| C-Cl vibrations | 772.634 -1 | 776.85 -1 |
There is only one vibrational mode for C=C in the monohydrated product - this is obviously because one alkene has been hydrogenated, therefore loosing one vibrational mode. The vibrational mode lost seems to be the one synonymous to the diene's 1740 cm-1 mode. Therefore, the weaker C=C bond (less strong vibration) has been hydrogenated. The monohydrated diene has a slightly stronger remaining C=C bond. This is due to addition of some excess electron density into the endo C=C bond.
The C-Cl vibrations are similar but again the monohydrated diene has a stronger C-Clσ bond due to movement of electron density into the σ orbital from the C=C π* orbital.
Mini Project - The Study of a Bicyclo-Octane using DFT-based Molecular Orbital Theory
|
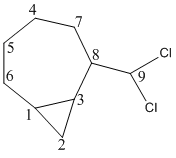
The molecules to be studied were exo and endo isomers of 2-dichoromethylbicyclo[4.1.0]octane (shown above). [10]
When bicyclo [5.1.0] octane is reacted with dichlorocarbene (an insertion reaction), the isomeric product ratio is 71:29 (endo:exo). Using computational methods, the 13C NMR and molecular vibrations were calculated. From the data, the isomers of the chosen molecule can be identified and studied. |
13C NMR data
Both isomers were geometrically optimised using a DFT method. The NMR was 'run' in SCAN in a chloroform solvent.
| endo-2-dichlorobicyclo[5.1.0]octane | δ(ppm) 17.3 (C3), 21.7 (C4), 24.8 (C8), 25.2 (C7), 26.7 (C2), 28.6 (C1), 32.2 (C6), 53.1 (C5), 85.0 (C9) | lit. δ(ppm) 15.1 (C3), 15.7 (C4), 17.9 (C8), 29.1 (C7), 30.8 (C2), 31.2 (C1), 31.7 (C6), 53.4 (C5), 78.7 (C9) |
| exo-2-dichlorobicyclo[5.1.0]octane | δ(ppm) 14.0 (C3), 15.9 (C4), 18.1 (C8), 23.9 (C7), 26.4 (C2), 27.7 (C1), 32.7 (C6), 50.3 (C5), 86.9 (C9) | lit. δ(ppm) 14.0 (C3), 15.6 (C4), 17.5 (C8), 25.6 (C7), 27.4 (C2), 29.1 (C1), 30.9 (C6), 49.2 (C5), 80.3 (C9) |
There are differences between the literature values and calculated values. Any value that has a difference of >5ppm to the literature means there is probably a difference in conformation between the calculated and experimental molecules. Possibly the reference peaks give rise to the difference in chemical shift, although there is not a uniform difference in ppm and some peaks fit quite well. For the endo isomer, carbons 4 and 9 have a difference in ppm of more than 5. Carbon 9 is the methyl carbon so the position of the methyl can easily be out or the difference could be in rotation of the C-CCl σ bond. Carbon 4 could be in a different conformation due to ring-flipping. Carbon 9 in the exo isomer has a 5ppm error compared to literature for the same reasons as highlighted for the endo isomer. Key differences (Δδ>2ppm) between the endo and exo isomers are at C3, C4, C8, C9 and C5. This difference enables us to differentiate between the two isomers. The most significant difference is at carbon 8. Clearly this shows us that the exo isomer is much more deshielded at this point than the endo isomer. If you look down the C8-C9 σ bond you can see a large difference in the geometry of the two isomers. The exo isomer is much closer to a planar structure than the endo isomer, which perhaps explains the deshielding of the carbon at the 8 position and all the other carbons (except C9 and C6).
Vibrational Data
The vibrational/IR spectra of the isomers was obtained simply by calculating the vibrational modes using the b3lyp/6-31G method. The errors quoted for this method are 8% for high frequency modes (i.e. stretches) and it is presumed that the bending frequencies (i.e. low frequency) will have an even higher error. In the same method, the free energies of the molecules were calculated: ΔG(exo) = -797925.2 kcal/mol, ΔG(endo) = -797909.2 kcal.mol.
| endo-2-dichlorobicyclo[5.1.0]octane | ν(cm-1) 3086, 3027, 1411, 1294, 1253, 1233, 1221, 1109, 1098, 1032, 1012, 869, 855, 810, 754, 729, 728, 709, 622 | lit. ν(cm-1) 3064, 2995, 2925, 2853, 1285, 1219, 1027, 926, 840, 805, 736, 680 |  |
| exo-2-dichlorobicyclo[5.1.0]octane | ν(cm-1) 3222, 3144, 3141, 3138, 3130, 3101, 3088, 3084, 3073, 3060, 3049, 3044, 3032, 3029, 1512, 1406, 1362, 1285, 1261, 1253, 1035, 980, 952, 842, 795, 726, 714 | lit. ν(cm-1) 3077, 2991, 2914, 2857, 1463, 1444, 1291, 1224, 1086, 1072, 1019, 780, 756, 732, 708 |  |
NB - In this table, values ranging from 2800-3300 correspond to C-H stretching (assymmetric or smmetric); values ranging from 1600-1080 cm-1 correspond to bending, scissoring and rocking of C-H bonds; the stretch and bend of C-C bonds, is shown in the fingerprint region
Obviously, the values reported in literature are picked out as the peaks are of highest intensity and the most relevant. Similarly, only the calculated vibrations with high intensity (>5) vibrational modes have been reported. Taking into account errors, we cannot possibly spot correlation between literature and calculated vibrations. We can only make rough comparisons. One distinct difference is the lack of C-H assymmetric/symmetric stretching of alkanes in both isomers which does appear in the literture at ~2990 cm-1. Why has this been missed out by the b3lyp/6-31G method? The error for stretches was quoted at approximately 8%. If we look at the high values (>3080cm-1) of wavenumber with no correlation to literature, the " minus 8%" answer to these values are more similar to the expected C-H stretching frequency. Also, looking at the animations corresponding to these values we can see they do correspond to stretches. In fact, the highest wavenumber of both isomers corresponds to the assymmetric stretching of the cyclopropane C-H bonds.
Both isomers have quite similar vibrational modes. Due to the large error associated with the calculation, the only difference I would like to point out is the number of vibrational modes of each isomer. In literature and in our calculations, the exo isomer has the most vibrational modes. Therefore we cannot look at the modes themselves to distinguish the isomers but instead we look at the number of modes.
Mechanistic Selectivity
As previously mentioned, these isomers are synthesised by the insertion on dichlorocarbene into the C-H bond next to the cyclopropane ring. The product is either endo or exo, as we know. The product ratio is 71:29 (endo:exo). Both isomeric products are equatorial. Why is this when we have calculated the classical minimised energy of the isomers, showing the endo has a higher energy (MM2 endo: 34.9 kcal/mol, MM2 exo: 22.6 kcal/mol)? There must be a stabilisation effect in the endo isomer that is undetected by MM2.
If we look at the dihedral angles in ChemBio3D we can see that there are two favourable anti-periplanar configurations in the endo isomer with the C4-C5-C9-Cl and the C6-C5-C9-Cl atoms. There are also app conformations in the exo isomer but they are on the other side of the ring which is not chemically important to us here. The app conformations with the Cl atoms are probably more stabilising than just C-H app conformations due to the increased size and polarisability of the Cl substituent.
Key References
- ↑ Arthur G. Schultz, J. Org. Chem., 1986, 51 (6), pp 838–841 DOI:10.1021/jo00356a016
- ↑ Stéphane Leleu et al, Tetrahedron: Asymmetry 15 (2004) 3919–3928 DOI:10.1016/j.tetasy.2004.11.004
- ↑ E. Smith, 2nd Year Organic Chemistry Lecture Course, Imperial College 2008
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319 DOI:10.1016/S0040-4039(00)92617-0
- ↑ Modern Physical Organic Chemistry, Eric V. Anslyn and Dennis A. Dougherty, University Science Books, 2006
- ↑ M. Fernandes, F. Fache, M. Rosen, P.-L. Nguyen, and D. E. Hansen, 'Rapid Cleavage of Unactivated, Unstrained Amide Bonds at Neutral pH', J. Org. Chem., 2008, 73, 6413–6416 DOI:10.1021/jo800706y
- ↑ J. Suggs, Tetrahedron Letters, Volume 38, Issue 13, 31 March 1997, Pages 2227-2230 DOI:10.1016/S0040-4039(97)00330-4
- ↑ B. Halton and S. G. G. Russell, J. Org. Chem., 1991,56, 5553. DOI:10.1021/jo00019a015
- ↑ B. Halton, J. CHEM. SOC. PERKIN TRANS. 2, 1992, 447 DOI:10.1039/P29920000447
- ↑ U. H. Brinker et al, J. Org. Chem. 2007, 72, 8434-8451 DOI:10.1021/jo7013356