Module 3 Bethan Matthews

Cope Rearrangement Tutorial

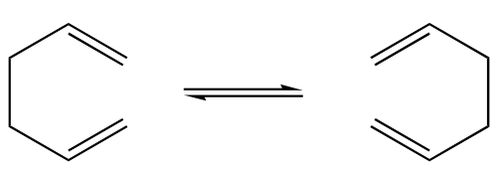
Figure 1: Simple scheme showing the cope rearrangement which will be studied in the following tasks.

The Cope rearrangement shown above is a simple rearrangement, but it has quite an interesting transition state. The transition state is in the form of a six-membered ring, which means it may exhibit a chair- or boat-like conformation. These two conformers are different in energy, and have very different structures. The overall aim of this tutorial is to get a basic understanding of the types of calculations required, and also to find the activation energies for each transition state, from one particular starting conformation. ^[1]

Optimizing the Reactants and Products

This section firstly optimises the 1,5-hexadienes using HF/3-21G methods, and comparing their relative energies. The table below shows the molecules, their energies and point groups. The energies were found by checking the method summary, and the point groups were found by selecting "Symmetrize". The Jmols are available from the conformation name.

Table 1: Comparison of the different conformations of 1,5-hexadiene and their energies as calculated using HF/3-21G methods.
Conformation	Energy (Hartrees)	Relative Energy (kJ mol^-1)	Point Group	D-SPACE
Anti1	-231.6926	0.167	C₂	Anti1
Anti2	-231.6925	0.335	C_i	Anti2
Anti3	-231.6891	9.414	C₂h	Anti3
Gauche1	-231.6877	13.849	C₂	Gauche1
Gauche3	-231.6927	0.000	C₁	Gauche1

The anti2 conformation was then further optimised at the B3LYP/6-31G(d) level, and the energy here was -234.6117 Hartree. This is slightly lower than the previously optimised structure (D-SPACE). The structures are almost identical, but I think the tighter optimisation method causes a slight moving of the hydrogen atoms on the central carbons. Anti2 Jmol. This optimised molecule was then submitted for frequency analysis (D-SPACE) which allows us to confirm the structure is at a minimum. The frequencies were analysed to check they were all "real" and there were no imaginary frequencies.

This method also allows us to determine some thermochemical data about the structure (all in Hartrees):

Electronic and zero-point energies: -234.4692
Electronic and thermal energies: -234.4619
Electronic and thermal enthalpies: -234.4609
Electronic and thermal free energies: -234.5007

The electronic and thermal energies value includes a correction which takes into account the extra energy at room temperature. These values are typical of the kinds of energies used to calculate the activation energies as seen later on.

Optimizing the "Chair" and "Boat" Transition Structures

Half the transition state was drawn and optimised under HF/3-21G method (D-SPACE) and this was then duplicated to form a guess of the entire chair transition state. Jmol

This was then optimised under HF/3-21G, to a TS (Berny) and with the force constants calculated once (D-SPACE). The frequency analysis gives an imaginary frequency at -817.96cm^-1, which corresponds to the formation and breaking of the bonds. Jmol

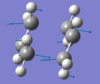
Figure 2: Imaginary frequency which corresponds to breaking and forming of bonds.

The same guessed transition state structure was then submitted for optimisation using the frozen coordinate method with the bond lengths set to 2.2Å D-SPACE). This returned it with bond lengths in the region of 2.13Å. This was then submitted again for optimisation, but this time to optimise the bond-forming distances (D-SPACE). Here the bond breaking and forming distance was optimised to be 2.02Å.

The Boat TS was then optimised, using a QST2 method. After some manual manipulations: (D-SPACE)

To find which conformation the transition states we have found lead to, we run an IRC calculation. Initially, it was run with 50 steps, and this did not give a minimised structure (D-SPACE):

Figure 3: IRC calculations for the chair transition state - didn't reach a minimum.

It was then run again with recalculating the force constatns every few steps, and this brought it much closer to a minimum (D-SPACE):

Figure 4: IRC calculations for the chair transition state.

To calculate the activation energies for the reaction to each transition state, the molecules were optimised using B3LYP/6-31G* methods and then submitted to frequency analysis.

The following is a summary of the activation energies and thermochemical energies for the relevant structures.

Table 2: Summary of thermochemical energies of the chair TS, the boat TS and the anti1 conformation (as calculated using B3LYP/6-31G(d) in hartrees.
Quality	Chair TS	Boat TS	Anti1
electronic and zero-point energies	-234.4150	-234.4023	-234.4693
electronic and thermal energies	-234.4090	-234.3960	-234.4620
electronic and thermal enthalpies	-234.4081	-234.3951	-234.4610
electronic and thermal free energies	-234.5009	-234.4318	-234.4693

Table 3: Summary of activation energies as calculated from above, compared with the experimental values in kcal mol^-1.
TS	0K	298.15K	Experimental at 0K ^[2]
Chair	34.1	33.3	33.5±0.5
Boat	42.0	41.4	44.7±2.0

The values calculated are agreeable with literature results, showing that this is an effective way of calculating the theoretical activation energies.

The Diels-Alder Cycloaddition

The Basic Diels-Alder Cycloaddition

First the butadiene molecule was optimised using AM1 semi-empirical methods, to give the planer structure shown. (Jmol, D-SPACE). The molecular orbitals were then analysed, in particular the HOMO and LUMO, (D-SPACE).


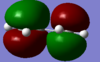
LUMO = 0.01797, symmetric	HOMO = -0.34456, anti-symmetric

Figure 5: Imaginary frequency corresponding to the new bonds formed.

The transition state was then optimised to B3LYP/6-31G(d), based on the best guessed structure as indicated, (Jmol, D-SPACE). The attainment of a transition state was confirmed by the presence of an imaginary frequency at -525.12cm^-1. This corresponds to the forming of the new bonds in a synchronous manner. The length of the partially formed bonds is 2.27Å; in comparison, a typical π_C=C bond is 1.33Å and a typical σ_C-C bond is 1.54Å.

If we follow the reaction pathway, we can see that this transition state does lead to a sensible product, with an energy minimum, and a gradient approximately equal to zero, (D-SPACE).

Figure 6: IRC pathway energy and gradient graphs.

Again the molecular orbitals were examined. This time, we can attribute the formation of some of the molecular orbitals to the combination of the butadiene-ethene HOMO/LUMO pairs. We are used to combining orbitals of identical symmetry to form molecular orbitals, and this holds true here, symmetric orbitals must be paired with symmetric orbitals, and anti-symmetric with anti-symmetric.


LUMO = -0.00861, symmetric	HOMO = -0.21896, symmetric	HOMO-1 = -0.22107, anti-symmetric
Butadiene LUMO + Ethene HOMO	Combination of two other symmetric orbitals, possible mixing?	Butadiene HOMO + Ethene LUMO

Cyclohexadiene and Maleic Anhydride Diels-Alder Cycloaddition

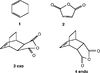
In the above prototype reaction, there was no regioselectivity, ethene molecule could approach either way round relative to the butadiene and the same product would still be formed. In this reaction, there is substituents on both the diene and the dienophile, so there are two possible products. ^[3] Cyclohexadiene (D-SPACE) and Maleic Anhydride (D-SPACE) were both optimised individually initially, to B3LYP/6-31G(d) level, and then combined to form the TS. There are two possible ways to combine the reactants, the endo and exo forms, see figure 7. The transition states were then optimised to the same level, to a Berny TS using a fixed coordinate method. The two different transition states will (hopefully) lead to two different products. The ''exo'' form, (D-SPACE), will theoretically be higher in energy than the ''endo'' form, (D-SPACE).

The transition states should have an imaginary frequency each, corresponding to the formation of the new bonds, these are as follows: Exo: D-SPACE Exo: D-SPACE

Table 4: Summary of imaginary frequencies and energies in the *endo* and *exo* transition states.
Exo	Endo

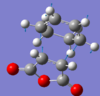-448.38cm^-1	-447.03cm^-1
-612.6793 a.u.	-612.6834

From this, you can clearly see that the endo transition state is lower in energy, which means that this is the kinetic product, as it is formed faster than the other form, due to a lower activation energy. We can consider the molecular orbtial interactions in the transition state, and this explains why this is lower in energy.

Table 5: Summary of the molecular orbitals of the transition states.
Form	D-SPACE	LUMO	HOMO
Exo	D-SPACE	-0.07844,anti-symmetric	-0.24214,anti-symmetric
Endo	D-SPACE	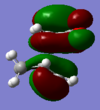-0.06773,anti-symmetric	-0.24228,anti-symmetric

In the HOMO and LUMO there is little secondary orbital effect, but this does not rule out the possibility that there is a large stabilisation in any other orbitals, so the cause for the endo preference may be due to steric effects. If we look at the structures of the transition states, the endo form has partially formed bonds which are 2.27Å in length, and in the exo form they are 2.29Å. There is slight Van der Waals repulsion between the maleic C=O carbon and the hydrogen as shown below, as the sum of their VdW radii is 2.90Å, larger than the separation distance. This does not occur in the endo form, as the pair is not as close (opposite ends of the molecule!) and the other hydrogens are not close enough to cause an effect. However, there is a much smaller, but still repulsive, VdW between the hydrogens as shown below, as the sum of their VdW radii is 2.40Å. This smaller destabilisation results in the endo form having a lower energy transition state.

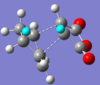Possible exo VdW repulsions.	Possible endo VdW repulsions.

To check that these transition states lead to suitable products we can run an IRC and see that a minimum is formed. As the gradient reaches zero, we can assert that the curve has reached a minimum, ie. the product. Also looking at the structures produced, there seems a suitable progression to a suitable product, so the transition state found above seems vaguely correct.

If we consider the energies of the products:

Exo: -612.7558 a.u.
Endo: -612.9042 a.u.

Here, the endo form has a lower energy, which means that this is the thermodynamic product, as well as the kinetic product.

References

↑ Hoffmann R. and Stohrer, W.D.; J. Am. Chem. Soc.; 1971; 93; 6941
↑ Wiest, O., Black, K.A. and Houk K.N.; J. Am. Chem. Soc.; 1994; 116; 10336
↑ Craig, D., Shipman, J.J. and Fowler, R.B.;

[1] Hoffmann R. and Stohrer, W.D.; J. Am. Chem. Soc.; 1971; 93; 6941

[2] Wiest, O., Black, K.A. and Houk K.N.; J. Am. Chem. Soc.; 1994; 116; 10336

[3] Craig, D., Shipman, J.J. and Fowler, R.B.;

[1]

[2]

[3]