Rep:Mod:3516464

Module 1: The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

Aims

The aim of module 1 was to demonstrate how molecular modelling techniques may be used to rationalize the results of reactions, and to predict alterations to reactions and new types of reactions. Allinger MM2 molecular mechanics models implemented in ChemBio3D were used to predict the geometry and regioselectivity of the hydrogenation of cyclopentadiene dimer and the stereochemistry and reactivity of an intermediate in the synthesis of Taxol. Modelling using semi-empirical molecular orbital theory method MOPAC PM6 and Gaussian for DFT methods were used to explore the regioselective addition of dichlorocarbene, and glycosidation in monosaccharide chemistry. To conclude the module, a mini-project was carried out to investigate spectroscopic stimulation in organic molecules to differentiate isomers.

Modelling using Molecular Mechanics

Introduction

Molecular systems can be modelled using Newtonian mechanics with the Molecular Mechanics (MM) approach, where force fields are used to calculate the potential energy of systems. This computational method where assumes that the energy of a molecular system consists of five independent terms: diatomic bond stretches and triatomic bond angle deformations (each expressed as a Hookes Law potential), tetra-atomic bond torsions, non-bonded Van der Waals repulsions (expressed as a Lennard-Jones potential) and electrostatic attractions of bond dipoles. The total energy of the molecular system is the sum of these terms, thus these mathematically simple functions allow ease of computation. The MM model attempts to minimize this total energy by optimizing the geometry for a specified molecular system.

The final energy for a system obtained with the MM2 model used in Module 1 is not related to any thermodynamic quantity, and comparison between energies produced by different force fields is not possible. However, isomers may be compared when energies are obtained from the same force field. The MM model is suitable when considering simple hydrocarbons, but for non-classical systems such as aromatics, summation of the five independent terms is not applicable, thus semi-empirical molecular orbital theory methods must be employed instead.

The Hydrogenation of Cyclopentadiene Dimer

The Diels Alder cycloaddition of two cyclopentadiene produces a dimer, which can potentially be one of two stereochemical isomers (fig 1). This is because the reactants may approach each other in two orientations: the exo approach, where the substituent on the dienophile may be directed away from the diene, or the endo approach, towards the diene.

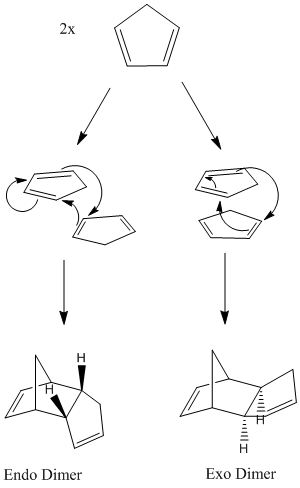
                                              Figure 1: Formation of cyclopentadiene dimer

The endo product is preferentially formed. In order to rationalize this observation and to determine whether the reaction is under thermodynamic or kinetic control, MM2 force field was used to optimize the geometries of the two products. The results are displayed below in Table 1.

Table 1 - Comparison of energies of the exo and endo dimers using MM2 force field

Interaction	Energy of exo dimer/ (kcal/mol)	Energy of endo dimer/ (kcal/mol)
Stretch	1.2855	1.2507
Bend	20.5794	20.8476
Stretch-Bend	-0.8381	-0.8358
Torsion	7.6571	9.5109
Non-1,4 Van der Waals	-1.4171	-1.5430
1,4 Van der Waals	4.2322	4.3195
Dipole/Dipole	0.3776	0.4476
Total Energy	31.8766	33.9975

The results of Table 1 indicate that the exo dimer is the thermodynamically stable product, as its total energy is lower than that of the endo dimer (31.8766 kcal/mol compared to 33.9975 kcal/mol). The main contribution to this energy difference appears to be the torsion interaction (7.6571 kcal/mol for the exo dimer compared with 9.5109 kcal/mol for the endo dimer), and this is due to the position of the pair of hydrogens (illustrated in figure 1) in relation to the bridgehead of the molecule. For the exo dimer, the hydrogen pair is situated on the opposite side to the bridgehead, whereas the hydrogen pair is located on the same side as the bridgehead for the endo dimer, causing greater steric hindrance.

Since it is the endo dimer which is preferentially formed, this suggests that the reaction is under kinetic control. Studying the exo and endo transition states can give an explanation to this selectivity, as for the endo transition state, the secondary orbital overlap is the greatest. The endo transition state is more stable, and thus the endo dimer is preferentially formed.

Hydrogenation of the endo dimer can produce one of two dihydro derivatives (figure 2), compound 3 and compound 4. The geometries of the two dihydro derivatives were optimized with the MM2 force field, and the results displayed in Table 2.

                                               Figure 2: Dihydro derivatives

Table 2 - Comparison of energies of the dihydro derivatives, compound 3 and compound 4, using MM2 force field

Interaction	Energy of compound 3/ (kcal/mol)	Energy of compound 4/ (kcal/mol)
Stretch	1.2380	1.0965
Bend	18.7894	14.5236
Stretch-Bend	-0.7518	-0.5494
Torsion	12.7052	12.4981
Non-1,4 Van der Waals	-1.3318	-1.0679
1,4 Van der Waals	6.0483	4.5124
Dipole/Dipole	0.1632	0.1406
Total Energy	36.8605	31.1521

The data of table 2 suggests that compound 4 is the thermodynamic product, as its total energy is lower than that of compound 4 (31.1521 kcal/mol compared with 36.8605 kcal/mol). The largest contribution to this difference in energy is the bend interaction, which is 4.2658 kcal/mol greater for compound 3 than for compound 4. There is also a significant contribution from the 1,4 Van der Waals interactions, which is 1.5359 kcal/mol greater for compound 3 than for compound 4. These energy differences can be attributed to the difference in location of the double bonds, and relief of strain of the sp2 centre in a 5 membered ring, compared with that which is next to a strained bridge head. Therefore it can be rationalized that compound 4 is the more stable dominant product, and the hydrogenation reaction is under thermodynamic control.

                                              Figure 3: Tetrahydrogenation product

It is noted that the tetrahydrogenation product is formed after prolonged hydrogenation. From comparing the energies of the tetrahydrogenation product with compounds 3 and 4 (table 3), it is evident that the tetrahydrogenation product is the highest in energy, and so stability has decreased when both double bonds are saturated. The main contribution to the loss in stability is the increase in torsional strain, compared with a small decrease in bend strain. Furthermore, the planarity of the molecule is lost after the tetrahydrogenation, and so the 1,4 Van der Waals contributions increase, when the hydrogen atoms are brought closer together.

Table 3 - Results of MM2 minimization on the tetrahydrogenated product

Interaction	Energy of tetrahydrogenated product/ (kcal/mol)
Stretch	1.1121
Bend	12.8846
Stretch-Bend	-0.4780
Torsion	17.0076
Non-1,4 Van der Waals	-1.3483
1,4 Van der Waals	6.0964
Total Energy	35.2744

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

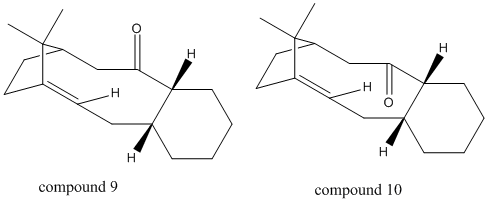
The synthesis of Taxol involves a key intermediate which can exist in the form of two atropisomers (compounds 9 and 10), where the carbonyl group either points up or points down:

Figure 4: Intermediates of Taxol synthesis, Compounds 9 and 10

Atropisomerism describes molecules that differ distinctly due to restricted rotation about a single bond, usually due to steric hindrance increasing the kinetic barrier for free rotation. For the taxol intermediate, atropisomerism arises due to the position of the olefinic bond next to the bridge head, which causes hyperstability and steric hindrance. It has been observed that upon standing, the compound converts to the alternative atropisomer, suggesting that the kinetic product is formed first, before isomerization occurs to form the thermodynamic product. In order to determine the stability of the two atropisomers, MM2 and MMFF49 force field were used to analyse compounds 9 and 10.

Compounds 9 and 10 contain a six membered ring, which may exist in the chair form, or the higher energy twist boat form. The results of the MM2 and MMFF49 optimization are displayed in table 4.

Table 4: Results of optimization of the Taxol intermediate using MM2 and MMFF49 methods

Interaction	Energy of Compound 9 [twist boat](kcal/mol))	Energy of Compound 9 [chair](kcal/mol))	Compound 10 [twist boat](kcal/mol)	Compound 10 [chair](kcal/mol)
Stretch	2.8776	2.6343	2.7102	2.6210
Bend	17.2785	12.5590	11.7409	11.3377
Stretch - Bend	0.4733	0.4247	0.3235	0.3427
Torsion	21.38	19.1228	21.8732	19.6806
Non-1,4 Van der Waals	-1.6114	-2.1030	-2.1030	-2.1681
1,4 Van der Waals	14.3766	12.8610	13.9203	12.8711
Dipole-Dipole	-1.7084	-1.7017	-2.0314	-2.0020
Total Energy(MM2)	53.0099	44.2888	46.4337	42.6829
Total Energy(MMFF49)	77.9718	63.2767	66.3501	60.5668

The results of table 4 confirm that for Compounds 9 and 10, the twist boat conformation for the six membered ring causes a higher energy for the molecule than the chair conformation. When calculated with MM2, the twist boat conformers had total energies of 53.0099 kcal/mol (9) and 46.4337 kcal/mol (10), compared with the total energies for the chair conformers, which were 44.2888 kcal/mol (9) and 42.6829 kcal/mol (10). When calculated with MMFF49, the twist boat conformer energies were 77.9718 kcal/mol (9) and 66.3501 kcal/mol (10), compared with the chair conformer energies of 63.2767 kcal/mol (9) and 60.5668 kcal/mol (10). It is observed that energies calculated with MMFF49 are higher than calculation using MM2, but relative energies are the same. This is because both methods use different parameters to optimize molecular geometries, and so energies calculated by different force fields may not be compared. Therefore it can be concluded that the lower energy more stable chair conformers exist in appreciable amounts, over the twist boat conformers.

The data of table 4 shows that compound 10 is the thermodynamic product, as it is lower in energy than compound 9 when calculated with both MM2 and MMFF49. The energy difference between the two atropisomers may be attributed to not only the position of the carbonyl group, but to the olefinic bond situated adjacent to the bridgehead. It would normally be expected that such an olefinic bond would react readily, due to the adjacent bridgehead causing strain at the sp2 centre. On the contrary, the olefinic bond is unusually difficult to functionalise,causing hyperstability in the molecule. The hyperstability of this molecule was explained by modelling the hydrogenated form of compound 9. The double bond in compound 9 (chair) was saturated, and MM2 optimization was applied (results displayed in table 5).

Table 5 - Comparison of energies of compound 9 and its hydrogenated form using MM2 force field

Interaction	Energy of Compound 9 (chair))(kcal/mol)	Energy of saturated compound 9(kcal/mol)
Stretch	2.6343	3.2795
Bend	12.5590	17.1727
Stretch-Bend	0.4733	0.7624
Torsion	19.1228	23.1882
Non-1,4 Van der Waals	-2.1030	-1.0555
1,4 Van der Waals	12.8610	16.3213
Dipole/Dipole	-1.7017	-1.7420
Total Energy	44.2888	57.9266

Table 5 shows that the increased energy of the hydrogenated form indicates that the process is not thermodynamically favourable, due to hyperstabiity. Large contributions to the increased total energy of the functionalised alkene were torsion and bend energies. This indicates that the olefinic bond reduces torsional and bend strain in the molecule. Comparing the bond angles at the sp2 (125^o) and sp3 (117^o) centres, this shows that it would be energetically unfavourable to change an sp2 centre to an sp3 centre through functionalization of the olefinic bond, as the more acute sp3 bond angle causes greater strain in the molecule. Another large contribution to the increased energy of the saturated form are the 1,4 Van der Waals forces. This is due to the increased number of hydrogen atoms upon saturation, thus setting up more repulsive interactions.

Figure 5: Bond angles

compound 9

hydrogenated form of compound 9

Modelling using semi-empirical theory

Introduction

The molecular mechanics methods become insufficient when modelling electronic interactions of a molecule, thus semi-empirical molecular theory can be used instead. Semi-empirical molecular orbital theory approximates some of the integrals used in the solution of Schrodinger's equation, to estumate the energy of molecules as a function of the electron distribution and geometry. To compensate for these approximations, empirically derived parameters are introduced to allow calculated results to be in agreement with observed spectroscopic or molecular properties.

Regioselective addition of dichlorocarbene

To demonstrate the transition from a classical treatment of molecules with a quantum mechanics approach that includes the wave description of the electrons, the regioselective addition of dichlorocarbene with compound 12 was studied (figure 6).

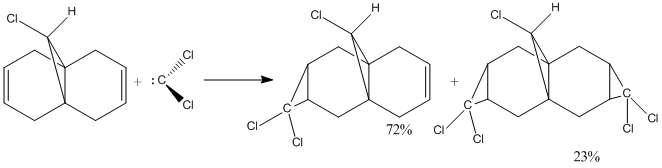
Figure 6: Addition of dichlorocarbene with compound 12

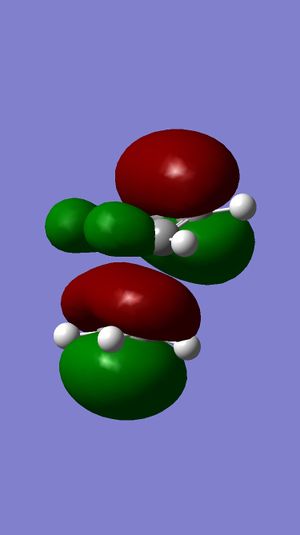
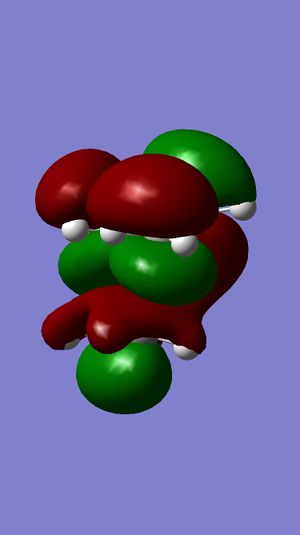
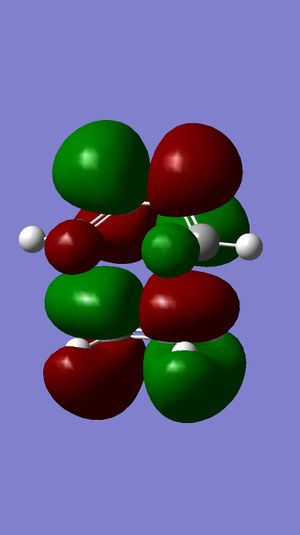
The syn tri chloride is the major adduct (72%), and this may be explained by analyzing the molecular orbitals of compound 12. Thus the HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 orbitals were modelled using the MOPAC/PM6 method to investigate the pi selectivity of this reaction. MM2 was firstly used to optimize the geometry of compound 12, before the MOPAC/PM6 and Gaussian interface were used to minimize the energy and calculate the energy of molecular orbitals. The molecular orbitals have been displayed graphically:

Figure 7: Molecular Orbitals of Molecule 12

HOMO-1

HOMO

LUMO

LUMO+1

LUMO+2

For electrophilic additions, electron density is donated from one of the double bonds in compound 12 into the LUMO of an electrophile. Therefore, the HOMO of compound 12 determines the reactivity towards the dichlorocarbene electrophile. It can be seen from the HOMO of compound 12 that there is great electron density on the the syn C=C pi bond, but no electron density on the anti C=C pi bond. The LUMO of compound 12 shows that there is a large proportion of electron density at the pi antibonding C=C double bond. From the HOMO, it is evident that the syn double bond will be most susceptible to electrophilic attack, whilst the LUMO shows that the anti double bond will be susceptible to nucleophilic attack. This explains why the electrophilic addition of dichlorocarbene occurs mainly at the syn double bond.

Another reason for the stability of the anti double bond to electrophilic addition is that the the C-Cl σ* bond is close in energy to the C=C π-bond. This is due to the electronegativity of the chlorine atom lowering the energy of the σ* bond, and so a stabilizing interaction with the anti double bond is established. As illustrated by the molecular orbitals, the LUMO has positive overlap with the electron density over the anti double bond on the HOMO-1 orbital. This corresponds to donation from the anti C=C π-orbital (on the HOMO-1) to the anti-periplanar C-Cl σ*-orbital (LUMO+1). This stabilizes the HOMO-1 orbital, making it too low in energy to be react with most electrophiles. The anti double bond can react only once the syn double bond has reacted, which is why the minor product is formed (32%).

Furthermore, donation into the C-Cl σ*-orbital increases the anti-bonding character of the C-Cl bond and weakens it. The influence of the C-Cl bond on the vibrational frequencies of the molecule was explored. Vibrational frequencies of compound 12 and its hydrogenated product where the anti double bond is replaced by a C-C single bond were computed using a density functional approach. Both compounds were subjected to B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation. The stretching frequencies of compound 12 and its dihydro derivative are found in table 6.

Table 6 - Main stretching frequencies of compound 12 and its dihydro derivative

Derivative	Image	C-Cl/ cm-1	anti C=C/ cm-1	syn C=C/ cm-1
Di-alkene		770.6	1737.0	1757.35
Mono-alkene		774.9	-	1758.1

Figure 8: IR spectra

IR spectrum of compound 12

IR spectrum of dihydro derivative of compound 12

The IR data shows that the C-Cl stretch occurs at a higher wavenumber for the mono alkene (774.9cm^-1 ) than for the di-alkene (770.6cm^-1 ), which means that the C-Cl bond is stronger when only the syn double bond is present. This supports the previous idea of the electron density from the anti C=C bond donating into the C-Cl σ*-orbital (figure 7), weakening the C-Cl bond. When the anti C=C bond does not exist, as in the mono alkene, the C-Cl bond is thus strengthened.

Monosaccharide chemistry: glycosidation

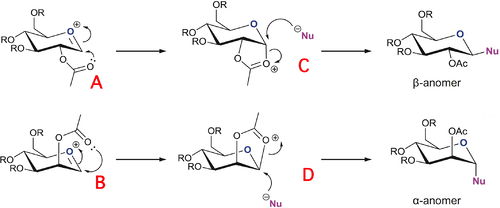
Glycosidation involves replacing the 'X' group with a nucleophile Nu (figure 8). Different anomers are produced, depending on the orientation of the adjacent acetyl group. This is known as the 'neighbouring pair effect'. For the β-anomer, the intermediate oxonium cation must be attacked from the bottom face, to then allow a nucleophile to come in from the top face. Similarly, the α-anomer is formed by the acetyl oxygen attacking from the top face of the oxonium cation, allowing the nucleophile to come in from the bottom face. Thus glycosidation reactions are very stereospecific, and produce the 1,2 trans product almost exclusively. However, there are two conformers to each intermediate, as the acyl group may point below (A, B) or above the plane (A', B') of the oxonium cation, which means that diastereoisomeric products may be produced from each intermediate. Similarly, C and D may exist as conformers where the oxonium ring points below the plane of the molecule (C and D) or above the plane of the molecule (C' and D')

Figure 9: Reaction scheme for formation of A, B, C and D

A limitation to MM2 force field is that the method does not take bond conjugation into account, which is important for this exercise as the acetyl group that attacks in the neighbouring group participation mechanism is conjugated. Thus MOPAC/PM6 methods would be more suitable for optimizing the geometries of A, A', B, B', C, C', D and D', as the classical approach of MM2 would not take into account the effects of neighbouring group paticipation, necessary for analysis of the regioselectivity of the glycosidation reaction.

An appropriate R group to choose when modelling the monosaccharides and their derivatives A, A', B, B', C, C', D and D' would be methyl. The smaller number of electrons afforded by a methyl group compared with an acetyl group reduces the computational demand. Acetyl groups are involved in hydrogen bonding, which is absent from methyl groups, leading to greater ease of geometrical optimization.

Table 7: Results of optimization of the monosaccharides and derivatives using MM2 and PM6 methods

Interaction	Energy of A (kcal/mol))	Energy of A'(kcal/mol))	Energy of B(kcal/mol)	Energy of B'(kcal/mol)	Energy of C (kcal/mol))	Energy of C'(kcal/mol))	Energy of D(kcal/mol)	Energy of D'(kcal/mol)
Stretch	2.8274	2.4675	2.6164	2.4206	2.0746	2.7915	1.9044	2.7078
Bend	11.8841	11.7409	12.1053	10.0962	14.2000	18.5044	21.2475	20.6617
Stretch - Bend	1.0756	-0.956	1.0372	0.9097	0.7548	0.8835	0.8147	0.8668
Torsion	3.1460	19.1228	1.2575	2.2262	9.7712	9.0645	7.4787	7.8782
Non-1,4 Van der Waals	1.4620	-11.4251	-1.0464	-2.1103	-2.2416	-2.0903	-2.8255	-2.6533
1,4 Van der Waals	18.9647	19.8610	17.9735	18.9722	18.8509	19.0523	16.6689	18.3094
Charge-Dipole	-25.6110	-11.9787	-19.33	-5.7562	-5.7541	-0.3551	-7.6125	-1.1538
Dipole-Dipole	5.9110	4.0392	5.5390	4.0077	-2.0543	-1.4382	-1.8625	-1.1269
Total Energy(MM2)	19.6845	29.7826	30.2178	30.5848	33.1262	46.4094	35.6384	45.4897
Total Energy(PM6)	-91.66227	-77.41679	-88.73038	-77.51017	-91.66185	-66.84285	-88.52602	-67.00343

The results of table 7 show that conformers A and b, where the acetyl group points below the plane of the oxonium ring were lower in energy than conformers A' and b', where the acetyl group points above the plane of the oxonium ring. The main interactiosn that cause the energy difference are the charge-dipole interactions, which increase when the acetyl group points up as the orientation of the polar oxygen atoms on the acetyl group is less energetically favourable, due to increased electrostatic repulsions.

Similarly, conformers C and D, where the oxonium ring pointed below the plane of the molecule, were more stable (lower in energy) than conformers C' and D' where the oxonium ring pointed above the plane of the molecule. The conformers C' and D' are unstable and so do not undergo the nucleophilic addition to produce the final product. This instability is reflected in the strain at the molecular bridges of C' and D', when the acetyl bridge is in a trans position rather than cis.

''Figure 10: Bond angles

C conformer bond angle: 106 degrees

C' conformer bond angle: 101 degrees

The bond angles at the bridgehead illustrate how the C' conformer is more strained, and so less stable than the C conformer. Furthermore, MM2 treatment of C and C' shows that there is an increased bending contribution to the total energy of C', emphasizing that it is strain that contributes greatly to the instability of C'.

Structure based mini project using DFT-based orbital methods

The total synthesis of (-)Cubebol

As well as predicting the outcomes of reactions by analyzing the energies of molecular systems, the previously used techniques can allow us to distinguish between isomers of a product. By using DFT-based molecular orbital methods, spectroscopic data for molecular systems can be predicted, and then used to verify the experimentally gained results. The problem chosen to be explored for the mini project was the synthesis of Cubebol. The synthesis could lead to many potential isomers, but the pair of diastereoisomers chosen for analysis were:

Figure 11: Diastereoisomers of the product Cubebol

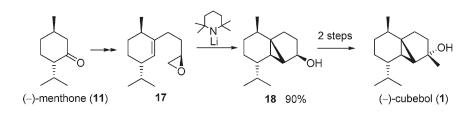
Cubebol, a natural sesquiterpene alcohol, can be synthesized from methone with the following steps:

Figure 12: Reaction scheme for synthesis of cubebol

The key spectroscopic techniques used to identify which isomer was formed were optical rotation, NMR and IR . The calculated results were compared with the literature results, in order to determine which isomer of Cubebol was formed by synthesis from menthone. The diastereoselectivity of the synthesis was rationalized by analyzing the energy of possible intermediates of the synthesis.

NMR analysis

Figure 13: ¹³C NMR spectra

NMR spectrum of isomer 1 (DOI:10042/to-9541

NMR spectrum of isomer 2 DOI:10042/to-9542

Figure 14: Assignation of carbons in isomers 1 and 2

Isomer 1

Isomer 2}

Table 8: Comparison of Carbon 13 NMR data

Carbon no	δliterature	Isomer 1: δcalculated	Isomer 2: δcalculated
8	80.3	79.1	80.9
3	44.1	42.1	40.6
9	39.0	37.7	39.0
7	36.3	37.2	36.0
12	33.6	34.6	35.9
1	33.4	34.6	35.8
5	31.7	33.7	32.8
6	30.8	32.5	30.9
10	29.5	31.7	27.6
16	27.9	27.1	27.4
4	26.5	26.4	25.8
2	22.5	25.8	24.9
13	20.1	22.2	22.5
14	19.6	21.3	21.9
11	18.7	21.2	20.7

Figure 15: Graph 10 to compare the variation of calculated results with literature values

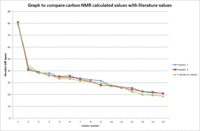The NMR spectra of both isomers were computated by firstly optimizing the geometries using MM2, MOPAC and then Gaussian DFT method. The standard used for this computation was CDCl₃ as this was the standard used in the literature. The accuracy of this method is 3-5ppm. No additional corrections to the data for spin orbit coupling errors was required, as there are no heavy halogen atoms in the compounds. Table 9 shows that the data collected are within 3-5ppm of the literature values. The values are very close together, as shown in graph 10 where on average both graph lines corresponding to the isomers are very close to the literature value graph line, indicating that both isomers 1 and 2 could feasibly have been formed in the synthesis of cubebol. However, to give a greater indication of diastereoselectivity of the synthesis reaction, more spectroscopic data is required.

Vibrational analysis

Figure 16: IR spectra

IR spectrum of isomer 1

IR spectrum of isomer 2

The one IR stretching frequency included in the literature corresponds to the OH stretch of 3380cm^-1. It can be observed from the results that whilst the corresponding stretch for the OH in the two isomers differs from that of the literature, two distinct stretching frequencies are produced for isomer 1 and 2, 3165 and 3176cm^-1 respectively, which contributes to determining the presence of isomers. However, IR spectroscopy to distinguish between the two diastereoisomers is less useful than the NMR or optical rotation, as there is less distinction between significant stretches.

Optical Rotation

The wavelength of light chosen for this measurement was 589 nm, the solvent was CHCl₃.

Table 9 - optical rotation of the isomers 1 and 2 compared with the literature values

'Compound	Optical rotation / o
Isomer 1	65.52
Isomer 2	-30.46
Literature	-48.4

The results of table 9 show that the calculated value of isomer 2 is closer in value to the literature result than isomer 1, indicating that in the synthesis of cubebol, it is likely that isomer 2 is preferentially formed. Thus optical rotation was the most useful method of determining which isomer was likely to be formed in the synthesis, as there is a great distinction between the optical rotation of the two isomers. Optical rotation is a highly sensitive method for computational analysis as it is very sensitive to conformation, and so even a 60^o rotation of an OH group can change the reading by a factor of two. This is especially significant for the analysis of isomers 1 and 2, since the difference between them is a 180 degree rotation of the OH group.

Rationalizing diastereoselectivity

To rationalize the preferential formation of isomer 2 over isomer 1, MOPAC/PM6 was used to determine the relative stabilities of the two isomers. For isomer 1, a value of -72.75649 Kcal/Mol was calculated, whilst for isomer 2, a value of -81.54558 Kcal/Mol was recorded. The lower energy of isomer 2 suggests that it is the more stable product, and so would be more likely to be preferentially formed.

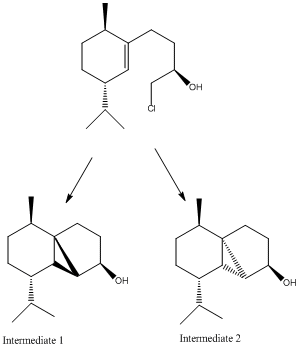
There are many possible isomers that could be formed during the synthesis of cubebol. One such possibility arises during the following step:

Figure 17: Intermediates 1 and 2

Such isomers could be formed as the reaction to form the intermediate isomers could occur above or below the plane of the molecule. To determine why the synthesis of cubebol does not proceed via intermediate 2, the energies of both intermediates were analysed with MOPAC/PM6. The results of the modelling were that intermediate 1 was calculated to have an energy of -38.12810 kcal/mol, whilst intermediate 2 was calculated to have an energy of 4.67657 kcal/mol. This indicates that intermediate 1 is more stable, so would be preferentially formed.

Conclusion

In conclusion, it was determined with optical rotation, NMR and IR spectroscopy, that in the synthesis of cubebol, isomer 2 was preferentially formed. Using MOPAC/PM6 to find the relative energies of the isomers indicates that isomer 2 is more stable than isomer 1. To further improve on this mini project, I would have looked at the energies of other possible isomers from this synthesis, and the intermediates involved to further explore the diastereoselectivity of the synthesis.