Rep:Mod:30706
Cope Rearrangement
Optimising Reactants:1,5-hexadiene
Anti Conformer
A molecule of 1,5-hexadiene with an "anti" linkage was drawn in GaussView and then optimised using the HF/3-21G method and %mem of 250MB. The calculation was then run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the anti conformer can be viewed here.
Total Energy: -231.68539621 a.u.
Point Group: C2h
Gauche Conformer
The predicted lowedt energy gauche conformer was drawn on GaussView and then optimised using the HF/3-21G method and %mem of 250MB. The calculation was then run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the gauche conformer can be viewed here.
Total Energy: -231.69266120 a.u.
Point Group: C1
Energy of Conformations
The anti-molecule is lower in energy than the gauche conformer because of stereoelcetronics. This is because the anti-peri-planar relationship is favoured due to the staggering of groups on the molecule.
Different anti structures were drawn to try and find out the lowest energy conformer.
| Energy | Point Group | Corresponding conformer in appendix | |
|---|---|---|---|
 |
-231.69097054 a.u. | C2h | Anti2 |
 |
-.231.69260235. | C2 | Anti1 |
It was found that the anti conformer that was optimised first had the lowest energy and therefore no further calculations were carried out. The first anti moelcule that was calculated and has the lowest energy corresponds to Anti3 in the appendix.
Ci Conformation
Optimisation
The Ci conformer of 1,5 hexadiene found and then otpimised with the HF/3-21G level of theory.The calculation was run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here.
Energy of Molecule: -231.69253528 a.u.
This agrees with the energy calculated previously of -231.69254 a.u.
The molecule was then optimised again using the DFT B3LYP/6-31G method. The calculation was run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the conformer can be viewed here. The overall geometry of the molecule does not change very much however there is a much larger change in the energy for the two conformers.
Frequency Calculation
The Frequency calculation was used on the optimised Ci molecule.
Low frequencies --- -17.9348 -11.6049 -0.7123 -0.0007 0.0004 0.0011 Low frequencies --- 70.2125 78.9912 115.3658
There are no imaginary (negative) frequencies in this molecule which confirms we have a ground state molecule instead of a transition state.
Sum of electronic and zero-point Energies= -234.416252 Sum of electronic and thermal Energies= -234.408952 Sum of electronic and thermal Enthalpies= -234.408008 Sum of electronic and thermal Free Energies= -234.447896
Optimisation of "Chair" and "Boat" Transition Structures
The C3H5 allyl fragments were optimised using the HF/3-21G method.The calculation was run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the Diels-Alder transition state structure can be viewed here. This was then used to form to starting structure.
Chair guess using Force Constant Matrix
The guess molecule was optimised and also frequency calculated by using OPT+FREQ, Optimisation to a TS (Berny), force constants calculated ONCE and keyword opt=NoEigen.The calculation was run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the chair transition state structure can be viewed here. This was then used to form to starting structure.
Low frequencies --- -817.9354 -2.0471 0.0003 0.0003 0.0007 1.0550 Low frequencies --- 2.4212 209.5283 395.9056 ****** 1 imaginary frequencies (negative Signs) ******
The frequency calculation produces one imaginary frequency of -817.93cm-1 which shows the vibration corresponding to the Cope Rearrangement and proves that we have a transition state structure.
Chair guess using Frozen Coordinate Method
The guess molecule was also calculated by using the frozen coordinate method by freezing certain C-C bonds to 2.2A. The molecule was then optimised. A three-dimensional image of the chair transition state structure can be viewed here. The imaginary frequency found was -817.99cm-1. This is very similar to the previous imaginary frequency calculated.
Bond forming/breaking distance: 2.02035 A.
Optimising Boat Transition State
The boat transition state was optimised using the QST2 method. The calculation was meant to fail however it suprisingly did not.The calculation was run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the boat transition state structure can be viewed here.
Low frequencies --- -839.9355 -4.6331 0.0009 0.0011 0.0012 2.5511 Low frequencies --- 3.1094 155.1798 382.0291 ****** 1 imaginary frequencies (negative Signs) ******
Only 1 imaginary frequency was found which tells us that we have a transition state.
Intrinsic Reaction Coordinate
The Intrinsic Reaction Coordinate follows the minimum energy path from a transition structure down to its local minimum on a potential energy surface. The frozen coordinate chair transition state was used for the IRC calculationusing the HF/321G method.The calculation was run on a HPC server and the results from the calculation was published onto D-Space.


The energy of the transisiton structure was -231.60280200 a.u.
However the IRC did not have the full amount of completed steps and did not calculate the minimum geometry. To improve the IRC calculation of the minimum geometry we can:
1. Take the last point on the IRC and run a normal minimisation
2. Restart the IRC and specify a larger number of points until it reaches a minimum
3. Compute the force constants at each step along the IRC
Activation Energies
The chair frozen coordinate structure was reeoptimised at the B3LYP/6-31G method. The molecule can be viewed here. (The file could not be published to D-Space).
The frequency calculation was then carried out.The calculation was run on a HPC server and the results from the calculation was published onto D-Space.
Low frequencies --- -562.1479 -0.0010 -0.0008 0.0006 20.7334 23.7227 Low frequencies --- 40.2421 192.4530 259.3808 ****** 1 imaginary frequencies (negative Signs) ******
Energy=-234.50546672 a.u.
The boat frozen coordinate structure was reeoptimised at the B3LYP/6-31G method. The molecule can be viewed here. (The file could not be published to D-Space).
The frequency calculation was then carried out.The calculation was run on a HPC server and the results from the calculation was published onto D-Space.
Low frequencies --- -236.7065 -109.7890 -34.0812 -10.0747 -0.0009 -0.0009 Low frequencies --- 0.0005 9.6923 27.0484 ****** 3 imaginary frequencies (negative Signs) ******
There are three imaginary frequencies which show that the optimisation has failed as we failed to find a critical point. This can be seen as the calculation hasn't fully converged.
Item Value Threshold Converged? Maximum Force 0.000129 0.000450 YES RMS Force 0.000028 0.000300 YES Maximum Displacement 0.011821 0.001800 NO RMS Displacement 0.002895 0.001200 NO Predicted change in Energy=-1.525463D-06
Energy=-234.44888631 a.u.
The geometries of the transitions states would not differ much. However the energies will differ a lot.
Diels Alder Cycloaddition
The Diels Alder reaction is a pericyclic cycloaddition reaction which is concerted and has no intermediates. The cycloaddition reaction is between an electron rich dienophile (cis-butadiene)and an electron-deficient diene (ethene). The π orbitals of the dieneophile form new σ bonds with the π orbitals of the diene. The HOMO/LUMO of one fragment interacts with the HOMO/LUMO of the other reactant to form two new bonding and anti-bonding MOs. However whether the reaction is allowed or forbidden depends on the number of electrons involved and the symmetry of the frontier molecular orbitals. The cycloaddition reaction is allowed if the electron count is 6 (4n+2, where n=1) and the symmetry of the HOMO and LUMO are the same, producing a significant overlap density.
Optimisation of cis-Butadiene
A molecule of cis-butadiene was drawn in GaussView and optimised using the semi-empirical AM1 method. The calculation was then run on a HPC server and the results from the calculation was published onto D-Space.
The calculation was fully convereged.
Item Value Threshold Converged? Maximum Force 0.000030 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000368 0.001800 YES RMS Displacement 0.000162 0.001200 YES Predicted change in Energy=-9.691185D-09 Optimization completed. -- Stationary point found.
Energy of the optimised structure: 0.04879719 a.u.
| HOMO (11) | LUMO (12) |
|---|---|
 |

|
| Symmetry= a | Symmetry=s |
The symmetry of the molecular orbital was either a, asymmetric with respect to the plane or s, symmetric with respect to the plane. This is important because only orbitals of the same symmetry are allowed to interact.
Computation of Transition State
The transition state of the cycloaddition of cis-butadiene and ethene was calculated using the guess, an envelope type structure that maximises the overlap between the ethylene π orbitals and the π system of butadiene. The envelope type structure was guessed by drawing the two fragments and freezing the interfragment C-C bond distances to 2.2Å. The guess structure was cleaned and then optimised to a minimum using the semi-empirical AM1 method, using the opt=ModRedundant keyword. The calculation was run on a HPC server and the results from the calculation was published onto D-Space.
| Original guess structure | Optimised guess structure |
|---|---|
 |

|
The optimised structure looks more similar to the transition state as the bonds are forming and breaking. This shows that the symmetry of the fragments are the same the reaction is allowed to proceed. The geometry of the structure has been fully converged:
Item Value Threshold Converged? Maximum Force 0.000056 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.001127 0.001800 YES RMS Displacement 0.000235 0.001200 YES Predicted change in Energy=-7.086448D-08 Optimization completed. -- Stationary point found.
The optimisation of the transition state was further carried out by unfreezing the C-C bonds, using an Opt+Freq calculation optimising towards a TS(Berny) with the semi-epirical AM1 method. The calculation was run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the Diels-Alder transition state structure can be viewed here.
The calculation was fully converged:
Item Value Threshold Converged? Maximum Force 0.000172 0.000450 YES RMS Force 0.000031 0.000300 YES Maximum Displacement 0.001280 0.001800 YES RMS Displacement 0.000374 0.001200 YES Predicted change in Energy=-1.449859D-07 Optimization completed. -- Stationary point found.
Energy of the optimised structure: 0.11165491 a.u.
It can be confirmed that the transition structure for the Diels Alder reaction has been obtained because there is only one imaginary frequency, -955.86 cm-1.
Low frequencies --- -955.8593 -2.9981 -0.0181 -0.0033 0.0224 4.1909 Low frequencies --- 8.0749 147.3741 246.7282 ****** 1 imaginary frequencies (negative Signs) ******
Discussion
Ethylene and cis-Butadiene Transition Structure
The HOMO and LUMO molecular orbitals for the Diels Alder transition structure are shown below:
| HOMO (17) | LUMO (18) |
|---|---|
 |

|
HOMO: This is antisymmetric about the central bond. The LUMO of ethene interacts with the HOMO of cis-butadiene with 1 node. This informs us that the end product of the reaction is antisymmetric.
LUMO: This is symmetric with respect to the plane along the central bond. The HOMO of ethene interacts with the LUMO of cis-butadiene with 2 nodes.
The Diels Alder reaction is allowed as the symmetry of the orbitals is conserved and therefore produces two sigma bonds.
The geometry of the transition structure is shown below. The ethene molecule approaches the cis-butadiene molecule face on in the correct symmetry to allow interaction to form the new sigma bonds.

| Bond | Bond Length (Å) |
|---|---|
| Ethene C=C | 1.38 |
| Diene C=C | 1.38 |
| Diene C-C | 1.40 |
| Partly formed σ C-C bond | 2.12 |
There is a small difference between the bond distances of the C-C and C=C bonds so therefore this proves that there is a delocalised transition state.
Typical sp3 C-C bondlength: 1.53Å
Typical sp2 C-C bondlength: 1.46Å
Van der Waals radius of a C atom: 1.60Å
Van der Waals forces are experienced when the two molecular orbitals overlap. As the radius of one Van der Waal's carbon atom is 1.60Å then when the two carbon atoms approach each other they start to undergo attractive interactions at 3.2Å. The distance between the partly formed σ C-C bond is 1.4 Å which is less than 3.2Å and therefore this is an attractive interaction.
| Negative Frequency (-955.86cm-1) | Lowest Positive Frequency (147.37cm-1) |
|---|---|
 |

|
The vibrations corresponding to the reaction path at the transition state is shown above. The formation of two σ bonds can be observed between the carbon atoms of ethene and the terminal carbon atoms of cis-butadiene. The formation of the two bonds is synchronous.
The lowest positive frequency shows separate molecular vibrations of the two fragments with no interaction between them. However the negative imaginary frequency shows an interaction between the two fragments as it displays the reaction pathway at the transition state to form the two new bonds and therefore the product.
Regioselectivity of the Diels Alder Reaction
Calculation of the Exo Transition State
The guess transition state of the Exo Product was drawn in GaussView. The bonds that are forming/breaking in the reaction were frozen at 2.2Å using the Frozen Coordinate Method. The molecule was optimised to a minimum using the semi-empirical AM1 method using the keyword opt=ModRedundant. The calculation was then run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the Diels-Alder transition state structure can be viewed here. The geometry of the calculated tsructure is similar to the predicted transition state.
The geometry of the structure has been fully converged:
Item Value Threshold Converged? Maximum Force 0.000026 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.001590 0.001800 YES RMS Displacement 0.000330 0.001200 YES Predicted change in Energy=-4.263699D-08 Optimization completed. -- Stationary point found.
The optimisation of the transition state was further carried out by unfreezing the C-C bonds, using an Opt+Freq calculation optimising towards a TS(Berny) with the Hartree-Fock 3-21G method and force constants calculated once and NoEigen keyword. The calculation was run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the Diels-Alder transition state structure can be viewed here.
The geometry of the structure has been fully converged:
Item Value Threshold Converged? Maximum Force 0.000112 0.000450 YES RMS Force 0.000014 0.000300 YES Maximum Displacement 0.001765 0.001800 YES RMS Displacement 0.000293 0.001200 YES Predicted change in Energy=-3.040359D-07 Optimization completed. -- Stationary point found.
It can be confirmed that the transition structure for the Diels Alder reaction has been obtained because there is only one imaginary frequency, -646.74 cm-1.
Low frequencies --- -646.7388 -5.6585 -4.1196 -2.9856 -0.0007 -0.0006 Low frequencies --- 0.0004 41.5071 131.1762 ****** 1 imaginary frequencies (negative Signs) ******
Calculation of the Endo Transition State
The guess transition state of the Endo Product was drawn in GaussView. The bonds that are forming/breaking in the reaction were frozen at 2.2Å using the Frozen Coordinate Method. The molecule was optimised to a minimum using the semi-empirical AM1 method using the keyword opt=ModRedundant. The calculation was then run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the Diels-Alder transition state structure can be viewed here. The geometry of the calculated structure is similar to the predicted transition state.
The geometry of the structure has been fully converged:
Item Value Threshold Converged? Maximum Force 0.000066 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.001784 0.001800 YES RMS Displacement 0.000284 0.001200 YES Predicted change in Energy=-6.034321D-08 Optimization completed. -- Stationary point found.
The optimisation of the transition state was further carried out by unfreezing the C-C bonds, using an Opt+Freq calculation optimising towards a TS(Berny) with the Hartree-Fock 3-21G method and force constants calculated once and NoEigen keyword. The calculation was run on a HPC server and the results from the calculation was published onto D-Space. A three-dimensional image of the Diels-Alder transition state structure can be viewed here.
The geometry of the structure has been fully converged:
Item Value Threshold Converged? Maximum Force 0.000129 0.000450 YES RMS Force 0.000018 0.000300 YES Maximum Displacement 0.001574 0.001800 YES RMS Displacement 0.000214 0.001200 YES Predicted change in Energy=-2.118080D-07 Optimization completed. -- Stationary point found.
It can be confirmed that the transition structure for the Diels Alder reaction has been obtained because there is only one imaginary frequency, -642.33 cm-1.
Low frequencies --- -642.3323 -0.0007 -0.0006 -0.0005 2.2610 2.4475 Low frequencies --- 5.0568 65.2663 142.0227 ****** 1 imaginary frequencies (negative Signs) ******
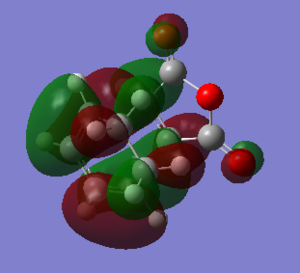
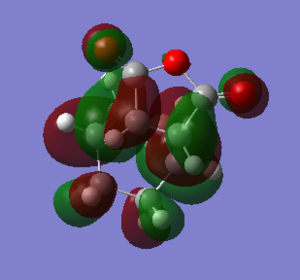
Both the exo and endo isomers have a HOMO which forms an antisymmetric orbital with one nodal plane. This is the correct symmetry requirement needed for the cycloadditon reaction to be allowed.
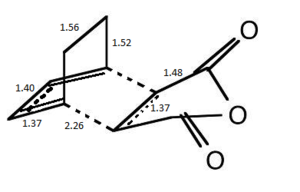
The structural differences between the exo and endo forms is that maleic anhyrdide interacts on a different face of the diene. in the exo isomer the maleic anhydride appraches from the top face but on the endo isomer the maleic anyhydride approaches from the bottom face. This results in the steric clashes. Therefore the endo isomer has a smaller C-C bond between the maleic anhydride fragment and the CH2- CH2 bridge componenet. The exo isomer is more strained due to the oxygen atoms on the maleic anhydride being very close to the CH2-CH2 bridge reuslting in a steric clash. This is not present in the endo isomer.
The secondary orbital overlap results in stabilisation of the the endo isomer. The secondary orbital overlap interactions allows overlap between the orbital of the C=O bond on maleic anhydride and an orbital on the CH=CH fragment resulting in stabilisation of the transition state. This can be seen by the endo isomer having electron density in this region but the exo isomer does not show any electron density. The relative energy of the endo form is lower than the exo form which means it is more stable and therefore the kinetic product. Both sterics and the secondary orbital overlap favour the endo product as the kinetically preferred product.