Rep:Mod:2sadr
Module 2: Bonding (Ab initio and density functional molecular orbital)
Sadia Rahman
Introduction
In this report computational chemistry will be used for analysing inorganic chemistry. This will help to get an insight into the structure and bonding of the complexes. These are more complex then the organic complexes looked at in a previous report. The analysis will help to differentiate between conformers by looking at the energy and then rationalise the stability. The transition states and activated complexes will not be able to be characterised. Therefore thermodynamic information will be looked at. The properties will be analysed using IR, dipole moments, electron density and molecular orbital’s to understand the bonding and local interactions between the atom.
The error values for the analysis has been defined by the program used and will used throughout the report. The energy will have an error of ~ 10 kJ/mol, the dipole moment will be accurate to ~ 2 dp, frequencies are conventionally reported with no decimal places and have a known systematic error of around 10%, as a harmonic approximation for vibrations are used when there is actually anharmonic vibrations, intensities are rounded to the nearest whole integer, bond distances ~ 0.01 Å and bond angles are to ~ 0.1° .
Borane (BH3)
Optimisation of BH3
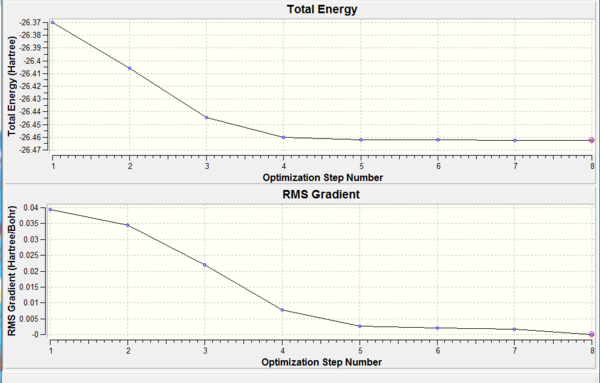
Initially a trigonal planar BH3 sturucture was created in Gaussview and the three B-H bond distances set to 1.5 Å. It was then optimised using DFT, the method was B3LYP and the basis set 3-21G. This can also be seen below, in the summary. The method BYLP determines the type of approximation made to solve the Schrödinger equation. The basis set determines the accuracy and is not very accurate, so the calculation time is short which was 27 seconds. This is the first step in the quantum mechanical calculation and has optimised the position of the nuclei. The summary also shows that the gradient is <0.001 indicating that the molecule has been optimised completely. The bond distance was optimised to 1.19 Å and the angle to 120o as expected for a trigonal planar molecule. The real output was also looked at to check if the job has converged and the relevant sections can be seen below, and is also here: File:BH3 optimisation.txt. It shows that the forces and displacements have converged. Therefore for small displacement the energy has not changed.

Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000015 0.001200 YES
Predicted change in Energy=-1.886451D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1944 -DE/DX = 0.0 !
! R2 R(1,3) 1.1944 -DE/DX = 0.0 !
! R3 R(1,4) 1.1944 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! A4 L(2,1,3,4,-2) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
For a more graphical view of the optimisation the graphs were looked at. The total energy graph shows the energy of the molecule at each step of optimisation, the graph below is the root mean square and it shows the gradient of it. The gradient graph goes to zero as the minimum energy is reached, which is at the 5th step. The gradient is the rate of change of energy with respect to the steps in the optimisation, so is the number of times the geometry of the molecule is changing. The molecule is now optimised and has a structure which is stable. This structure is the one which will be found in the gas phase. It could also be the one found in the solid structure but only when there are no solid sate forces or crystal packing forces which act to distort it.
Molecular Orbitals of BH3
The electronic structure of the molecule can now be looked at by analysis its molecular orbitals. These quantitative MO's can be used to compare them to qualitative ones via the MO diagram shown below. The optimised BH3 was used and the method changed to an energy calculation. The additional keywords added was "pop=full" and the MO analysis done. The MO calculation DOI:10042/to-6553 were ran for eight orbitals and has been added to the image below. The image below shows the qualitative MO diagram, drawn using the linear combination of molecular orbitals approach (LCAO) with quantitative molecular orbitals obtained from the calculation above. The energy of the computed levels is also shown below so that they too can be looked at to compare to LCAO relative energies.


The difference between the LCAO MOs and the computed ones are as follows:
MO 1: The LCAO and the computed show similar orbital for the 1s non-bonding orbital. This orbital however does not participate in the chemistry of the molecule.
MO 2: The LCAO has all the orbitals in the same phase which is the same for the computed result, however the computed one shows a combined single orbital.
MO 3: Again like MO 2 the orbitals have been combined together for the computed, but the phases and shapes are similar for both methods. In the computed the mixed s and p orbitals can be seen.
MO 4: Both methods show similar shapes as the computed has mixed the orbitals together.
MO 5: The computed method has the orbital occupying the whole molecule but the LCAO only the Boron, but the shapes are both p-orbitals.
MO 6: The shapes are fairly similar, but there is some difference due to the out of phase interactions. Also the 2e' was lower in energy then it should be in the comparison to the LCAO.
MO 7: The orbitals are again similar but the p-orbital is not as linear, as it is in the computed compared to the LCAO.
MO 8: The shapes are similar but the s-orbital for Boron is different in the computed then the LCAO. The 3a'1 is higher in energy in the computed then LCAO.
Overall both methods have similar orbitals, the computed orbitals show the mixing of the orbitals more clearly.
In terms of the relative energy levels of the MOs: the MO 6 and 8 have switched in energy but the molecular orbitals when switched match the LCAO orbitals better. The degenerate orbitals are therefore not the same. However the rest of the orbitals energy ordering matches and MO 3 and 4 are degenerate in both methods. The higher energy orbitals MO 6,7 and 8 ordering is different and in the computed they are alot more closer in energy then the LCAO represents. However the computed may differ if a different basis set was used.
The accuracy and usefulness of qualitative MO theory is good as they are very similar to the computed one, even considering the accuracy used. The general shape can be seen well with the LCAO but the exact energies are hard to get. It is therefore good to use as a simple prediction but the computational methods allow more precise information to be seen from the calculation. The LCAO also does not go beyond eight energy levels were as the computed method can calculate more of the excited states.
NBO of BH3
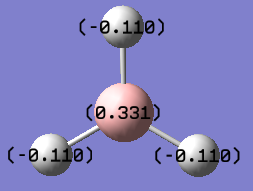
Natural Bond Orbital analysis will be done using the .log file, File:BH3 NBO.txt. It gives information about the charges as can be seen by the diagram below. The charge distribution can also be looked with colours where green is positively charge and red is negatively charge. The charge for B atom is 0.331 and on the H atoms is -0.110, the Boron atom is highly positively charged, so is a Lewis acid and the H is electronegative.It also provides information about the s and p character of the bonds as summarised in the table below.
| NBO | % Contribution B | % Contribution H | % Hybrdisation s | % Hybrdisation p |
|---|---|---|---|---|
| B1H2 | 44.49 | 55.51 | 33.34 | 66.66 |
| B1H3 | 44.49 | 55.51 | 33.34 | 66.66 |
| B1H4 | 44.49 | 55.51 | 33.34 | 66.66 |
| B core | 100.00 | 0.00 | 100.00 | 0.00 |
| B lone pair | 100.00 | 0.00 | 0.00 | 100.00 |
It can be seen from the table above that the boron has 1/3 s and 2/3 p character and so forms 3sp3 hybrid orbitals with the 3H. The mixing of the orbitals was also looked at with the "Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis". It illustrates the interactions from bonding NBOs into non-bonding eg B lone p orbital. It does not have much information for this compound, if the values in the E(2) column are greater than 20 kcal/mol then they are of interest. In this case it was 1.5 kcal/mol so there is no interaction between the lone pair of B and the anti-bonding orbitals.
Frequency of BH3
The vibrational analysis of BH3 will be looked at below. It is the second derivative of the potential energy surface and if the frequencies are all positive then it is a minimum. If one value is a negative frequency then there is a transition state and if there is more than one negative then there is no critical point found and the optimisation has not been completed. This analysis provides then IR data shown below. A frequency analysis will be done to ensure that the minimum energy structure has been produced. This calculation was carried out using the optimised molecule. The job type was changed to 'frequency' and additional key words as "pop=(full,nbo).
The summary energy was check to be same as the one recorded for the optimisation. The output file File:Bh3 freq.txt. The log file has the low frequencies of the molecule. They are usually zero but in this case are larger due to the method used. The largest "zero" frequency is roughly 40cm-1 which is an order of magnitude smaller then any of the normal vibrations so the results are reasonable. The animated vibrations were then looked at in Gaussview and the images are shown below, along with the IR spectrum. There are six vibrations and they are all positive indicating the structure has been optimised. In the IR there are only three peaks as there are two sets of degenerate vibrations: 1205 and 2730 cm-1, these are degenerate and give one peak each. The molecule has four different motions, but one has an intensity of zero (peak 4), as in the vibration there is no overall dipole change as it is A1'.

TIBr3
Optimisation of TIBr3
A similar process as above was done for TIBr3 however the symmetry was restricted by enabling the point group D3h and constraining it. Again it was run with DFT and optimised as shown by the summary below. Also a larger basis set and pseudo potential calculation was used for this section, as it is more complex then the molecule above. The gradient is close to zero so the molecule has optimised, as also check in the output file and graphically images.
The method used was DFT and B3LYP and the basis set used is the LanL2DZ which uses a medium level basis set D95V for the first row atoms and Los Alamos ECP on heavier elements. A better basis sets and pseudo potentials is not used as the calculation would be more complex and take much longer. The same method and basis set for both calculations, so that a comparison could be made.
The real output was also looked at to check if the job had converged (File:TiBr3 opt.txt) and the relevant section can be seen below. The TIBr bond distance was found to be 2.65 Å and the angle 120o as can be seen in the images below. A literature value for the distance was found as 2.52 Å [1], which is in good agreement with the calculated value.
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.102959D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! A4 L(3,1,4,2,-2) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad



Frequency of TIBr3
The TIBr3 was optimised and then the structure was confirmed to be a minimum by frequency analysis shown below. The frequency calculation was carried out so that the ground state could be established. The same method and basis set was used do the same accuracy level and data comparison could be done. The log file:File:TiBr3 freq.txt and the relevant information shown below. The low frequencies were small enough to support the minimum energy to be optimised, and are shown below. The lowest 'real' mode is 46cm-1, also the lowest frequencies are within the 10cm-1 of the expected zero value, therefore the calculation can be thought to be accurate.
Low frequencies --- -3.4226 -0.0026 -0.0004 0.0015 3.9361 3.9361 Low frequencies --- 46.4288 46.4291 52.1449
Bonds are not always considered in Gaussview, as they do not appear after being optimised, this does not mean a bond is not present. It is rather that the bond does not correlate to the bond distance in the database.
A bond is an interaction between two atoms or molecules which holds them together. It is therefore an electrostatic interaction. It is formed by two electrons and will form when atoms are at a particular distance. The atoms must have the correct symmetry in its orbitals and similar energies to form. A strong bond is such that there is good orbital overlap and the overall energy of the system is low. The atomic orbitals coming together to form the molecular orbital, where the two atoms are now chemically bonded together. Therefore a bond is used to observe the structure of the molecule but the actual bonding interactions are spread across the whole molecule.

In the IR there are only three peaks as there are two sets of degenerate vibrations: 46 and 211 cm-1, these are degenerate and give one peak each. The molecule has four different motions, but one has an intensity of zero (peak 4), as in the vibration there is no overall dipole change as it is A1'.
This is very similar to the BH3 as it too only has three peaks, where two are from degenerate vibrations. This is due to the symmetry group being the same. The huge difference between the two complexes is the size of the frequencies. The BH3 peaks are at 1205, 2591 and 2730cm-1 while TIBr3 is at 46, 52 and 211 cm-1. This is due to the bond lengths of TIBr3 being a lot larger and mass of the atoms greater so the frequency is a lot smaller, as it is a reciprocal relationship.
An organometallic complex
Introduction
Mo(CO)4L2 when L=PPh3 has four carbonyl absorption bands for the cis ligands and one band for the trans ligand. The reasoning behind why one has four and one one will be examined below. The calculation of the full molecule is expensive so the phenyl ring will be replaced with Cl, as they have similar electronic contributions. The relative thermal stability and spectral characteristics of the two isomers will be looked at. The isomer which is more stable and the vibrational modes looked at. It is know that the trans isomer is more stable due to thermodynamics, and this will be looked at. Frequency analysis will also be used to verify that the optimal structure has been reached and to analyse the stereo-chemistry by looking at C=O bonds. The structures can be differentiated due to their different point groups, which effects the IR frequencies. The C=O region is of interest, the cis is C2v and the trans D4h symmetry. This means that the cis with its C2v symmetry will give rise to four carbonyl peaks and the trans D4h symmetry just one. The difference in the peak number is due to the dipole moments of the structure, the larger the change in the dipole moment the greater the number of IR active peaks. This will now be investigated below.
Optimastion Mo(CO)4L2
These calculations are significantly more intensive that the ones carried out above, so the SCAN service will be used. The optimisations as carried out with three stages and each are described in turn below. The ground state structure of both the trans DOI:/10042/to-6574 and cis DOI:/10042/to-6575 isomers was optimised. This was done by using the B3LYP method and with a low basis set and pseudo-potential LANL2MB, to get the rough geometry. Also a loose convergence was used by using the additional keywords as 'opt=loose'. Both of the first optimised products can be seen below. The structures have come back without the P-Cl bonds but this does not mean the bonds do not exist. They have been optimised such that they are longer then the data in Gaussview, which has been programmed with organic chemistry in mind.
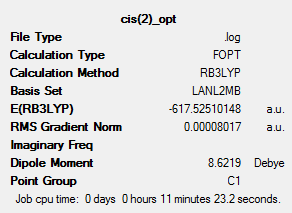
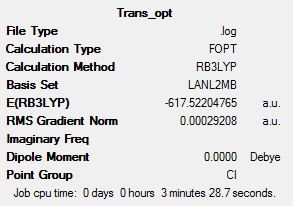
Optimisation for this low level generates good bond lengths and angles but the dihedral angles are not well defined. So the right orientation needs to be started at to get a better minima. The starting points are described below.
The optimised LANL2MB structures were taken and the torsion angle of the PCl3 groups changed. The cis conformer was altered so that one Cl pointed up parallel to the axial bond and one Cl from the other group pointed down. The trans conformer was optimised by have both PCl3 eclipsed and one of Cl in each group being parallel to one Mo-C bond, such that the torsion angle was 0o. The new geometries were then optimised using the B3LYP method with the LANL2DZ pseudo-potential for trans DOI:/10042/to-6576 and cis DOI:/10042/to-6577 and by using the additional keywords as "int=ultrafine scf=conver=9". This basis set is much better and has a better pseudo-potential as a much tighter convergence criteria.
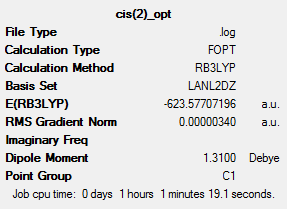
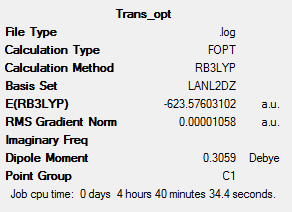
The LANL2DZ pseudo-potential and associated basis set are still not quite good enough to be used for the optimisation, due to the phosphorous atoms. The P likes to be hypervalent and uses low lying d orbitals. In this step this will now be accounted for by manually editing the log file from the optimisation above. The keyword "extrabasis" was added to the line: # opt b3lyp/lanl2dz geom=connectivity int=ultrafine scf=conver=9 extrabasis. Then at the bottom the following added:(blank line) P 0 D 1 1.0 0.55 0.100D+01 **** (blank line). The geometry was optimised and frequency analysis carried as shown below.


Taking a closer look at the optimisation,it can be seen that at the first two optimisations the more stable isomer was cis but then in the third it changed to the trans, as they are lower in energy. This optimisation has produced the correct stable isomer as agreed by literature. The trans isomer is more stable due there being less steric clash between the carbonyl and PCl3 ligands. The energy difference is calculated as follows: cis = -623.57707196 and trans = -623.69415609 au and as 1 Hartree= 2625.5 kJ/mol. Therefore cis = -1637202 and trans = -1637509 kJ/mol so the trans is 307 kJ/mol lower in energy then the cis. The error in the energy is about 10kJ/mol, the differences in the above in greater then this so a firm conclusion from the results can be made to agree with literature.
Here only thermodynamics has been considered but there may be kinetics cis playing a role, steric and electronic effects. Therefore computationally a clear isomer in terms of stability, can be reached. It can be thought that the cis isomer has more steric hindrance due to the PCl3 ligands and the axial positions in the trans complex is weakened by the trans effect by the electron withdrawing PCl3 group.
Bond lenghts and angles
The bond lengths and angles were obtain to analyse against literature and check that the optimisation had occur. Also to compare the two isomers. The literature in all cases were not the exact molecule but are just used to check the data. The trans complex was found to be the same and the literature [2] matches well. For cis a similar complex was found where the phosphine ligand was different, not all the data was found. These again were seen to be quite similar to the literature [3] indicating both complexes to have optimised. Taking a closer look it can be seen that the most significant difference is between cis bonds, but they are close enough. If the trans and cis bond are compared it can be seen that the Mo-C bond in the cis is stronger then the trans, vice versa for the Mo-P as the bond is shorter so stronger. This can be appreciated if the trans effect is considered as carbonyl ligands have strong trans effects.
| Bonds | Cis Bond length/ Å | Trans Bond length/ Å | Trans Literature Bond length/ Å | Cis Literature Bond length/ Å |
|---|---|---|---|---|
| Mo-C | 2.01 | 2.06 | 2.01 | 2.03 |
| Mo-P | 2.51 | 2.44 | 2.50 | 2.52 |
| P-Cl | 2.24 | 2.24 | 1.84 | - |
| C=O | 1.17 | 1.17 | 1.16 | - |
Now moving on to the bonds between the molecules, the P-Mo-P angle from the literature above was 97.54o due to steric interaction between the phosphine ligands. Other literature could not be found but a comparison of the two structures can be looked at. There are four C-Mo-C angles for the trans complex, this helps to understand the four peaks in the IR below.
| Bonds | Cis Bond angle/ 0 | Trans Bond angle/0 |
|---|---|---|
| P-Mo-P | 94.2 | 177.4 |
| C-Mo-C (opposite carbonyl) | 89.1, 89.7 | 180.0, 179.0 |
| C-Mo-C (adjacent carbonyl) | 90.5, 94.2 | 89.5, 90.5 |
Frequency Mo(CO)4L2
Using the optimised geometries the frequency analysis was carried out. There were no negative frequencies, indicating that the optimisation had occurred for both the trans DOI:10042/to-6615 and cis isomers DOI:/10042/to-6614 , and the ground state products had been found. The frequencies analysed are the C=O peaks and the two lowest energy modes, as shown in the table below. Below are the real vibrational modes, it can be assumed that the motions occur at room temperature as they are so low in energy.
| Vibrations | Description | Frequency / cm-1 | Intensity |
|---|---|---|---|
 |
Twisting around the P-Mo-P axis | 11 | 0.030 |
 |
Twisting of the PCl3 ligand | 18 | 0.007 |
| Vibrations | Description | Frequency / cm-1 | Intensity |
|---|---|---|---|
 |
Twisting of carbonyl ligands | 5 | 0.09 |
 |
Twisting of the PCl3 ligand | 6 | 0.00 |
The trans complex only has one C=O stretch as all the carbonlys are in the same environment. The lab experiment showed the peaks to be at 1890 and 2014 cm-1, these correlate to the values above. The main peak is around 1950 cm-1 as the first two peaks are degenerate as they are the antisymmetric stretch of the carbonyl ligand, so only one peak can be seen on the graph. The other two peaks have very low intensity so are not see on the spectra as there is no dipole change and they are totally symmetric modes. The literature data found was at 1896 cm-1 [3] and correlates well, indicating the product to have optimised well.

| Frequency / cm-1 | Intensity |
|---|---|
| 1950 | 1475.5 |
| 1951 | 1466.7 |
| 1977 | 0.6 |
| 2030 | 3.7 |
The cis complex has four carbonyl peaks and they are real and active. This is due to the point group of the group C2v, they give vibrational modes as they are totally symmetric with respect to the symmetry elements. The literature values [4] were at 1986, 1994, 2004 and 2072 cm-1, these also correlate well to the data below. They all have large intensities so there are four distinct peaks.

| Frequency / cm-1 | Intensity |
|---|---|
| 1945 | 762.9 |
| 1949 | 1498.3 |
| 1958 | 632.7 |
| 2023 | 597.8 |
Mini Project
The mini-project will look at 1,2 disilabenzenes which are benzene analogues synthesis from Si triple bonds. The 1,2-disilabenzene are planar structures and are aromatic. In the literature [5] the 1,2 and 1,3 substituted isomers were made in a 2:3 ratio. This ratio will be looked at to see if a thermodynamic analysis can be used to explain this as the kinetic analysis is to advanced to look at now. The aim for this part of the project will thus be to look at which isomer is more stable and compare it against the literature ratio. In the literature much larger R groups were used but for easy of calculation Me groups were used instead, this may effect the ratio and will be considered below.
Along side this investigation the benzene equivalents which are isoelectronic to with respect to the 4n+2 π electrons, will also be looked at to see how the energies vary from the same isomers but having a C=C instead of Si=Si bond. The energies will not be able to be compared but the relative stabilities of the isomers will be looked at and rationalised. Also an IR analysis done on the benzene molecules to see if it possible to differentiate between the two from the vibrations.
All four molecule was drawn using GaussView 3.0 and then saved as an input file and all the output files have been referenced below.
Optimisation
The method used for the calculation was an initially pre-optimisation with DFT B3LYP/3-21G then a second optimisation with B3LYP/3-211G due to the first being too simple to use as there are p-orbitals involved. After this was carried out on each of the four structures, a frequency calculation using the optimised molecule was done. The job type was changed to 'frequency' and additional key words as "pop=(full,nbo). The basis sets were kept the same so comparisons could be made between the isomers. They were check to be in the ground state by ensuring that there were no negative calculations, as if there were then a transition state would have been made.The Me group effect the vibrations as they have Me rotation .
If there files did contain any negative frequencies then they were re-optimised and send off for frequency calculations after the geometries were adjusted so that the methyl group has a zero dihedral angle between the ring. This was to minimise any sterics, and so the H's orbitals on the Me did not overlap. When the TS were found due to having negative frequencies and send for optimisation, it came back with lower energies as expected for the product to have a lower energy then TS state. The 1,3 and 1,2 referd to the phenyl ring substitutions.
| 1,2 disilabenzene | 1,3 disilabenzene | 1,2 benzene | 1,3 benzene | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
| ||||||||||||
| DOI:10042/to-6693 | DOI:10042/to-6694 | DOI:10042/to-6695 | DOI:10042/to-6696 |
| 1,2 disilabenzene | 1,3 disilabenzene | 1,2 benzene | 1,3 benzene | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
| ||||||||||||
| DOI:10042/to-6699 | DOI:10042/to-6700 | DOI:10042/to-6697 | DOI:10042/to-6698 |
The image below shows the summary data of each molecule so that the gradient could be check and the energies analysed after verifying that they were ground states, due to not having any negative frequencies. The time taken for each run can also be seen.

After ensuring the optimised structures were correct, the analysis could be carried out. Below the energy, bond length and angles will be analysed against literature and the stability of the products rationalised. The energy was converted to kJ/mol with the conversion of 1 Hartree= 2625.5 kJ/mol. It is know that the error in the energy is ~ 10 kJ/mol. The differences between the isomers is less then this so there maybe other effect which effect the ratio of the products.
If the energy analysis is done none the less then it can be seen that for the disilabenzene isomers the more stable product is the 1,3 disilabenzene product but for the benzene the 1,2 benzene isomer. The energies cannot be compared but the energy difference between the two isomers looked at closer. The benzene isomers have a larger energy difference between the two isomers so the stability of the stable product is greater. Due to there being no direct literature data is cannot be said for sure, but the ratio of the benzene products may therefore be less. If the literature data is looked at, the R groups have changed drastically but the isomer stability of the 1,3 disilbenzene substituted product is also higher as there is 3:2 ratio with 1,3:1,2 products. The R group has not effect the more dominant product but it cannot be said what the ratio will be.
| Molecule | Energy/ au | Energy/ kJ/mol | Energy difference / kJ/mol |
|---|---|---|---|
| 1,3 disilabenzene | -892.24617631 | -2342592 | - |
| 1,2 disilabenzene | -892.24473997 | -2342589 | 4 |
| 1,3 benzene | -389.50784028 | -1022653 | - |
| 1,2 benzene | -389.51013574 | -1022659 | -6 |
If the energy comparison is looked then the molecules which have a more negative energy are more stable and these have been highlighted above. This is different when looking at the pair of isomers. It can be seen that disilabenzene agrees with literature as the same product dominates but in benzene isomers this has switched so the 1,2 benzene analogue is more dominant. The energies can not be compared between the benzene and disilabenzene as they have different atoms, but the relative energy gap can be looked at and it can be seen that the energy gap between the disilabenzene is smaller then for the benzene so the interconversion between the two will be easier.
Bond length and angles
The bond lengths and angles were compared to the literature [5] data as shown below. They are very good agreement even if the R groups used are different, indicating the product to have optimised. The numbering can be seen in the image below.
The 1,2 disilabenzene and 1,3 disilabenzene have very similar bond lengths. The Si=Si bond is longer as is the Si-C in comparison to the C=C bonds in the ring this is due the larger size of the Si atom. The 1,2 disilabenzene is more symmetric then the 1,3 disilabenzene so both Si-C bond are the same. The error in the bond lengths is 0.01Å, so there is a difference in two bonds. This is between bond C4 and C5, this value is the same as the error, so can be ignored. The other bond is the Si(2)-C(3)where it is longer in the 1,3 disilabenzene as the Me group is substituted here causing the bond to lengthen due to the electron withdrawing nature of the group.
When comparing to literature Si=Si bond is can be seen that it is between 2.14 and 2.29 Å and are nearly 5 to 10% shorter than the Si-S. The data is also in agreement with the literature [6], and being aromatic as the length is in between a single and double bond.

| Bond | Lit Bond lenght/Å | 1,2 disilabenzene | 1,3 disilabenzene | Difference in isomers |
|---|---|---|---|---|
| Si1-Si2 | 2.20 | 2.21 | 2.21 | 0.00 |
| Si2-C3 | 1.80 | 1.81 | 1.83 | 0.02 |
| C3-C4 | 1.39 | 1.39 | 1.39 | 0.00 |
| C4-C5 | 1.45 | 1.44 | 1.43 | 0.01 |
| C5-C6 | 1.39 | 1.39 | 1.39 | 0.00 |
| Si1-C6 | 1.80 | 1.81 | 1.81 | 0.00 |
The bond lengths of the two benzene isomers were also looked at and theses both can be seen to be smaller then disilabenzene bond lengths. Here the significant difference in bond lengths is between C(4)-C(5) where the 1,3 benzene is shorter then the 1,2 benzene. This is due to the same effect as above as the Me group is one C(5) so causes the C=C bond to lengthen. When comparing the bond lengths to benzene which is 1.39 Å [7] it was seen that the bonds here have all lengthened by about 0.01-0.02 Å which is nearly the same as the error, this also proves that the product was optimised and shown that the disilbenzene bond lengths for the more part are longer. The only ones which have not been effect are C(3)-C(4) and C(5)-C(6) and they are one bond away for the Si=Si bond. The Si=Si bond length is 0.8 Å larger then the C=C, ,this is due the atom size increasing and its more diffuse nature.
| Bond | Lit Bond lenght/Å | 1,2 benzene | 1,3 benzene | Difference in isomers |
|---|---|---|---|---|
| C1-C2 | 2.20 | 1.41 | 1.41 | 0.00 |
| C2-C3 | 1.80 | 1.40 | 1.41 | 0.01 |
| C3-C4 | 1.39 | 1.40 | 1.40 | 0.00 |
| C4-C5 | 1.45 | 1.41 | 1.39 | 0.02 |
| C5-C6 | 1.39 | 1.40 | 1.40 | 0.00 |
| C1-C6 | 1.80 | 1.40 | 1.40 | 0.00 |
Finally the angles were looked at to again check the optimisation in comparison to literature and variation between the isomers. The literature matches well to the data below. The isomers is symmetric so the angles are too, between Si-C and C=C.
The 1,3 disialbenzene on the other hand is not symmetric. A similar effect to the bond distance increasing due to the substitutions, it also causes the angle to increase. The differences can be looked at, as they are greater then the error of 0.1 o.
| Bond | Lit Angles/o | 1,2 disilabenzene | 1,3 disilabenzene |
|---|---|---|---|
| Si1-Si2-C3 | 103.0 | 103.8 | 105.6 |
| Si2-C3-C4 | 133.2 | 129.7 | 123.6 |
| C3-C4-C5 | 123.8 | 126.2 | 131.6 |
| C4-C5-C6 | 124.1 | 126.2 | 126.6 |
| C5-C6-Si1 | 133.2 | 129.7 | 127.0 |
Frequency analysis
After the second optimisation, the frequency analysis was done to ensure the ground state products were found, so that there was no negative frequencies. These files can be seen below, some TS were found but the optimised files adjust by rotating the Me groups so they did not clash and sent off for optimisation again. This finally lead to all four IR's being found without any negative vibrations.
| 1,2 disilabenzene | 1,3 disilabenzene | 1,2 benzene | 1,3 benzene |
|---|---|---|---|
| DOI:10042/to-6701 | DOI:10042/to-6704 | DOI:10042/to-6703 | DOI:10042/to-6702 |
The IR analysis was carried out for the two benzene isomers. The isomer peaks do not vary a great deal, but a general trend can be seen that 1,3 benzene is usual at low numbers then the 1,2 benzene peaks. The suggest that the bond lengths are longer and less stiff which was the case seen from the analysis above, and there weaker bond in this complex then the other.
| 1,2 benzene frequency/ cm-1 | Intensity | 1,3 benzene frequency/ cm-1 | Intensity | Peak assignment |
|---|---|---|---|---|
| 901 | 15 | 885 | 16 | CH |
| 1042 | 21 | 1030 | 6 | CH2 wag |
| 1463 | 10 | 1463 | 5 | CH2 rock |
| 1537 | 46 | 1532 | 32 | CH2 scissor |
| 1550 | 19 | 1550 | 13 | C=C stretch |
| 3005 | 153 | 3006 | 90 | CH2 symmetric stretch |
| 3051 | 118 | 3046 | 36 | CH2 asymmetric stretch |
| 3092 | 76 | 3006 | 90 | CH3 |
| 3146 | 70 | 3146 | 43 | phenyl ring stretch |


Looking at the IR spectrum at a glance they are similar, but by taking a closer look the difference can be seen. The 1,2 benzene is the more symmetric product so will have less peaks in the IR spectra. The most varied region is the 3000 cm-1 and 1500 cm-1 which is the aromatic C-H and CH3 ring stretch and aromatic C=C stretches respectively. The IR could be used to distinguish between the two as the less symmetric isomer 1,3 benzene contains more peaks in both regions.
It has five peaks in the 3000 cm-1 region for the aromatic C-H and CH3 ring stretch and a distinctive doublet at 1500 cm-1 for the aromatic C=C stretches. In comparison to the 1,2 benzene which has four peaks in the 3000 cm-1 region for the aromatic C-H and CH3 ring stretch and a intense singlet compared to the distinctive doublet at 1500 cm-1 for the aromatic C=C stretches. Therefore the IR would be useful to distinguish between the two isomers.
NBO analysis
The NBO data was taken from the files:File:1,3disilabenzenenbo.txtFile:1,3benzenenbo.txt and the 1,3 disilabenzene and 1,3 benzene was looked at. Below the table can be seen of the charge densities of the two products. Each one will was looked at in turn and then compared. The numbering can also be seen below.
The images below show the charge density of both products with a colour code. The code is: bright green indicates highly positive charge and bright red highly negative charge. The Si atom is bright green so is highly positively charged, this can be understood as is it in the row below C in the period table so is less electronegative so will have more positive charge. This can be also be seen from the resonance structures below which shows how the charge can be distributed. The charge on the Si(0.796)= Si(0.735) whereas C(0.00003)=C(-0.00306), this clearly shows the more positive nature of the Si atom and bond. However this causes differences in the C substituted Me groups. This can be seen to then effect the carbon charge density adjacent to the atoms. If the CH carbon next to theses are looked at then in the disilabenzene the charge is -0.216 versus the benzene which is -0.046 and CH3 substituted carbon next to theses are looked at then in the disilabenzene the charge is -0.680 versus the benzene which is -0.435. In both cases the disilabenzene carbons are more negatively charged so will be even less favourable to nucleophillic attach then benzene is and more favourable then benzene to electrophillic attack.
The charge density data can be used to look at the build up of electron density and charge on the different atoms. If the 1,3 disilabenzene is looked at which has are larger range of charges. It can be seen that Si is by far the most positive and will be electron deficient, whereas the carbon atoms near by are negative. The H atoms around the ring and on the methyl are all positive but have a smaller value, as seen in the image and table below. In the molecule the Lewis base is the C and the Lewis acid the Si, this can be rationalised as Si is more electroposivite then C. This shows there is a strong charge separation with a positive Si and negative C. This polarisation occurs in the σ space as the π electron density distribution is very close to the nucleus, this was studied in literature[8]. The large charge separation could suggest that there may be kinetic stability or instability between the isomers.




There are many bonds in the complex but only one bond was looked at. The bonding contribution was also looked and the Si=Si and C=C bond looked at. It can be seen that about 50% contribution comes from each atom for both formation of the single and double bond. Also when looking a the hybridisation the single bond is sp2 in both cases as about 33% is from the s-orbitals and 66% from p-orbitals. In the literature [5] 29 Si NMR have low shift signal which characterised the sp2-Si, which is agreement with the data above.
The double bond is formed from 100% p-orbital in C=C completely but in Si=Si is slightly less, this maybe due to the orbital overlapping not being as efficient as they are more diffuse orbitals. Also this means π-bond is not a strong in comparison, so will be easier to break, thus more reactive. The similarity in the bonding can be used to justify the aromatic and planar nature of the disilabenzene and its analogy to benzene.
| NBO | % Contribution Si(1) | % Contribution Si(2) | Si(1) % Hybrdisation s | % Hybrdisation p | Si (2) % Hybrdisation s | % Hybrdisation p |
|---|---|---|---|---|---|---|
| Si1Si2 single bond | 49.68 | 50.32 | 31.69 | 68.31 | 32.07 | 67.93 |
| Si1Si2 double bond | 48.90 | 51.10 | 0.93 | 99.07 | 0.91 | 99.09 |
| NBO | % Contribution C(1) | % Contribution C(2) | C(1) % Hybrdisation s | % Hybrdisation p | C (2) % Hybrdisation s | % Hybrdisation p |
|---|---|---|---|---|---|---|
| C1C2 single bond | 50.16 | 49.84 | 35.25 | 64.75 | 35.24 | 64.76 |
| C1C2 double bond | 50.83 | 49.17 | 0.00 | 100.00 | 0.00 | 100.00 |
The geometry of the 1,3 disilabezene and 1,2 disilabebzenes are such that the geometries are similar to the Kekule structure as shown in the image below and stated in literature [8] . The Si-Si and two C-C bonds are double bonds as their bond lengths are close to the isolated bond lengths and the remaining C-C and C-Si bonds are slightly longer then the average single and double bonds. This implies that there is significant delocalisation of the π electron density in the molecule. The planarity as seen form the MO analysis below, also provides evidence for the conjugation within six electron π system. The image below also shows the zwitterion contribution of a disilabenzene molecule, there are four contributions and shows the inability to delocalise the Si-Si bond.

MO analysis
The MO of 1,3 substituted benzene DOI:10042/to-6707 and disilabenzene DOI:10042/to-6708 will be looked at below.Initially disilabenzene will be looked. The MO calculation were run by using the optimised file and same basis sets and changing the method to an energy calculation. The additional keywords added was "pop=full" and the MO analysis ran.
The MO of the molecule is quite complex but the number of electrons follows the Huckel rule: 4n + 2 π electron. The MO analysis showed that there were 45 occupied levels, so 90 electrons in the molecule. This full fills the rule with n=22.The aromatic nature can be illustrated by looking at the orbitals below. The four orbitals were looked at below as they are the more interesting one when it comes to reactivity. The MO of 1,3 benzene is also complex as there are 172 orbitals, so the same orbitals will be looked at. The MO analysis showed that there was 37 occupied levels, so 74 electrons in this molecule. This full fills the rule with n=18.The aromatic nature can also be illustrated by looking at the orbitals below.
The relative energies of the orbitals will not be compared but the HOMO-LUMO gap looked at and this energy compared. The image below is not to scale. The HOMO-LUMO gap for the disilabenzene is 0.155 and for benzene is 0.229 au, as 1 Hartree= 2625.5 kJ/mol so is 407 and 601 kJ/mol respectively. Therefore the HOMO-LUMO gap for 1,3 disilabenzene is smaller by 194 kJ/mol,thus it is more reactive, as the electrons can access the energy levels easier in comparison as the energy gap is smaller, and it will be more red shifted.
Looking at the bonding and non-boning orbital: in the 1,3 benzene molecule all the bonding orbitals have negative energies so the HOMO is the last negative orbital, whereas in 1,3 disilabenzene there are two non-bonding orbitals which are negative so the LUMO+1 is the last negative orbital.

1,3 substituted benzene and disilabenzene orbitals shapes are very similar, the disilabezne has larger orbitals due to the larger atoms in Si=Si. The MOs help to illustrate the aromatic nature of the complex and help to see that the structure is an benzene analogue as the electron delocalisation can be seen from the orbitals. If the orbital are looked the shape of the HOMO and HOMO-1 and LUMO and LUMO-1 are similar, this is the case for both complexes. They illustrate the electron clouds of the aromatic complexes.
The two highest bonding orbitals are both π MOs ( HOMO and HOMO-1) and the two lowest unoccupied anti-bonding orbitals are π * MOs (LUMO and LUMO+1).
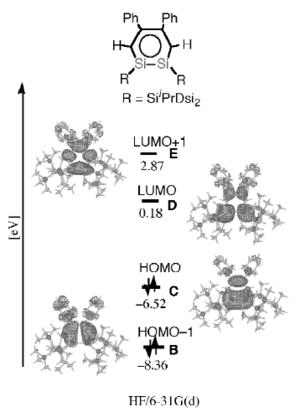
In the literature [9] the R group on the ring were Ph on the carbons and and SiiPrDsi2 on the Si=Si bond. The MO calculations were done using the method specified in the image below, this was also compared to benzene and it was seen that the HOMO-LUMO gap was smaller and more red shifted then benzene, this agrees with the data above. The energy levels below cannot be compared as different methods were used, but the relative HOMO-LUMO gap can be looked at and compared.
The HOMO-LUMO gap for the literature disilabenzene is 6.7 eV, 1 eV = 96.49 kJ/mol so is 646.483 kJ/mol, this indaicted that the R group changing effect the HOMO-LUMO gap hugely. Also in comparison the geometry, bonds and angles were very similar after changing the R group.
Conclusion
The mini-project enabled some interesting computational analysis to be done and some conclusions gathered from the comparison of the four compounds. The computational analysis at times could be quite length, but is a very useful technique which is reliable as the agreement to literature is good.
The disilabenzene compounds were both show to be analogues to the benzene from both MO, bond angle and distance analysis. The literature ratio of the products was proved for the disilabenzenes, but the analysis showed this was not the case for the benzene compounds. The R group was seen to effect the HOMO-LUMO gap and not the angles and bonds values. The IR analysis showed that the two isomers could be differentiated by analysis of the peaks. The charge density and bonding contribution allowed reactivity to be rationalised. Overall the project analysis enabled some ideas to be rationalised through computational methods.
References
- ↑ J Blixt, J Glaser, J Mink, I Persson, P Persson and M Sandstrom, J. Am. Chem. Soc, 1995, 117, 5089-5104
- ↑ G. Hogarth, lnorganica Chimica Acta, 1997, 254, 167-171
- ↑ 3.0 3.1 F. Cotton, D. Darensbourg, S. Klein, B. Kolthammer, Inorg. Chem., 1982, 21, 2661-2666
- ↑ E.C. Alyea and S.Song, Inorg. Chem., 1995, 34, 3864-387
- ↑ 5.0 5.1 5.2 R.Kinjo, M.Ichinohe, A.Sekiguchi, N.Takagi, M.Sumimoto, and S.Nagase, J.Am.Chem.Soc , 2007, 129, 7766-7767 Cite error: Invalid
<ref>tag; name "5th" defined multiple times with different content - ↑ R.West and M.J.Fink, J. Tetramesityldisilene, 1981,214, 1343
- ↑ Rev.Mod.Phys, 1958, 30, 150-162
- ↑ 8.0 8.1 K.K.Baldridge and M.S.Gordon , Journal of Organometallic Chemistry, 1984, 271, 369-379 Cite error: Invalid
<ref>tag; name "8th" defined multiple times with different content - ↑ A.Sekiguchi, Pure Appl. Chem., 2008, 80, 447-457