Rep:Mod:2cg507
Theory
Unless stated standard units are assumed
Creating and Optimising a Molecule
Gaussview was used to construct the desired molecule and Gaussian was then used to run the optimisation. An optimisation involves calculating a solution of the Scrödinger equation for the electron density and the energy, for a fixed position of the nuclei. In the optimisation the nuclei are moved around and a calculation of the electron density is performed for each of the fixed nuclei positions. The optimised structure represents the one with the lowest energy, the would be the minima on the potential energy surface of the molecule. At this point the nuclei and the electrons are in their equilibrium position, there are no forces acting to move their positions. Around this point the gradient of the potential energy curve will be zero and the equilibrium energy has been reached. Small changes to the positions of the nuclei and electrons around this point will have very little effect on the energy of the molecule and we now have our optimised structure.
Pseudo-potentials and basis sets
Using basis sets which include many different wavefunctions to describe the molecule allows a good accurate picture of the structure of a molecule to be predicted. When the molecules to be investigated start to get larger and contain heavier atoms, using high accuracy basis sets to accurately describe the entire molecule becomes computationally inefficient. In these cases we can use pseudo-potentials, which model the atom using only its valence electrons, which are the most significant electrons involved in bonding in these larger atoms and molecules.
BH3
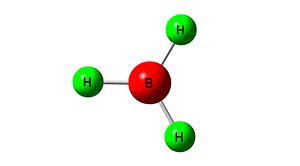
Using Gaussview the BH3 molecule was constructed, it can be seen to the right in the picture and also in a 3D rotatable jmol form. Using Gaussview the bond lengths of each B-H bond of the molecule were then increased from the standard length imposed by the program, to 1.5 angstroms. The molecule is then optimised.
Data provided from Gaussian following the optimisation of the molecule:
4 atoms 8 electrons neutral singlet
All B-H Bond lengths - 1.94
All H-B-H Bond angles - 120.0
The Gaussian optimisation of BH3 produces a Gaussian log file which can be viewed in Windows WordPad. This file contains all of the information recorded during the optimisation of the geometry. The method used for the optimisation was the B3LYP method using a basis set of 3-21G.
E(RB3LYP) = -26.462 A.U.
RMS Gradient Norm - 0.000000074 A.U.
Final Dipole Moment - 0.00D (all from z component)
Full point group - C2V
Time taken to perform the calculation - 53.0 seconds
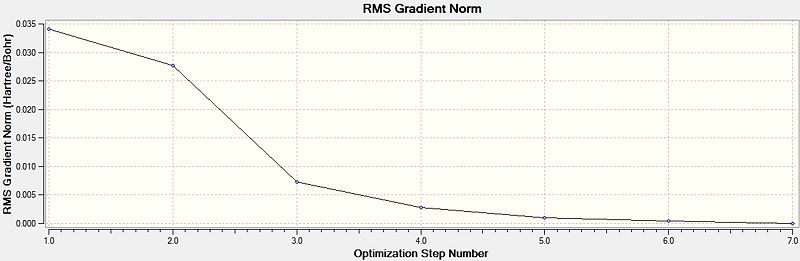
The method used determines the type of approximations used to calculate the Scrödinger equation and the basis set dictates the accuracy. The optimisation provides the position of the nuclei with the lowest energy for a particular electronic configuration. It can be seen that the optimisation is complete as the RMS gradient norm is close to zero, showing that small changes in geometry only involve a small change in energy around this point. The change in energy with the change in geometry can be seen on the two plots to the right. The optimisation shows that the trigonal planar structure is the lowest energy structure, with almost perfect 120 degree angles between the B-H bonds. This optimisation was performed very quickly as it is only a small non polar molecule.
Optimisation of BH3 file:
https://wiki.ch.ic.ac.uk/wiki/images/3/33/CG507BH3OPTIMISATION.LOG
Molecular Orbitals
Figure 1. Molecular Orbital diagram of BH3
| Molecular Orbital Analysis | |||||
|---|---|---|---|---|---|
| Molecular Orbital | LCAO Representation | MO Representation | Symmetry Label | Energy (kcal/mol) | Occupied? |
| 2 |  |
 |
a'1 | -0.482 | Yes |
| 3 |  |
 |
e' | -0.346 | Yes |
| 4 |  |
 |
e' | -0.317 | Yes |
| 5 |  |
 |
a''2 | -0.085 | No |
| 6 |  |
 |
a'1 | 0.063 | No |
| 7 |  |
 |
e' | 0.098 | No |
| 8 |  |
 |
e' | 0.146 | No |
The files for the Molecular Orbital analysis can be found hereDOI:10042/to-6587 . It can be seen from the above table that the molecular orbitals constructed via the LCAO method and the molecular orbitals from the Gaussian calculations are very similar, our predicted occupancies, as shown in the Molecular orbital diagram also agree with the Gaussian results. This shows that molecular orbital theory and the LCAO approach provide a very good approximation of the actual molecular orbitals. Using the molecular orbital LCAO approach is shown to be a worthwhile method that gives good results without the high computational demand of the quantum approach.
Natural Bond Orbitals
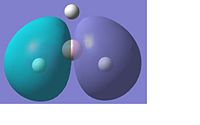
Atoms in the picture to the right are coloured by charge, bright green represented a high positive charge and bright red shows a highly negative charge. NBO analysis removes the delocalised electron density as shown in the molecular orbitals and formalises 2 electron 2 centre bonds.
NBO Charges:
B - 0.217 H - -0.066
When viewing the log file it can be seen that hydrogens 2 and 4 have a natural charge of -0.0657 while hydrogen 3 has a natural charge of -0.086. Below is the analysis of the natural bond orbitals obtained from the Gaussian log file. It shows the bonding involved in the molecule, here it can be seen that there are three bonds between the Boron and each of the three hydrogens. This data also shows the percentage contribution of each atom to the bond and the orbital character (hybridisation) of the atoms involved in the bond. Here the first bond has a 46.7% Boron contribution which has a 35.3% s and 64.7% p hybridisation. The hydrogen contributes 53.3% to the bond and has 100% s character. All three B-H bonds are similar with a slightly higher hydrogen contribution than boron contribution to the bond, this is reflected by the charge as most of the electron density lies on the Boron atom. The similarity in each of the bonds agrees with the bond lengths and angles between the bonds being equal.
1. (1.98513) BD ( 1) B 1 - H 2
( 46.67%) 0.6832* B 1 s( 35.28%)p 1.83( 64.72%)
0.0000 0.5940 0.0035 0.0000 0.0000
0.7071 0.0048 0.3836 0.0021
( 53.33%) 0.7303* H 2 s(100.00%)
1.0000 0.0000
2. (1.98620) BD ( 1) B 1 - H 3
( 45.67%) 0.6758* B 1 s( 29.44%)p 2.40( 70.56%)
0.0000 0.5425 -0.0076 0.0000 0.0000
0.0000 0.0000 -0.8399 0.0099
( 54.33%) 0.7371* H 3 s(100.00%)
1.0000 0.0009
3. (1.98513) BD ( 1) B 1 - H 4
( 46.67%) 0.6832* B 1 s( 35.28%)p 1.83( 64.72%)
0.0000 0.5940 0.0035 0.0000 0.0000
-0.7071 -0.0048 0.3836 0.0021
( 53.33%) 0.7303* H 4 s(100.00%)
1.0000 0.0000
4. (1.99953) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s( 99.99%)p 0.00( 0.01%)
6. (0.00000) RY*( 1) B 1 s( 0.00%)p 1.00(100.00%)
7. (0.00000) RY*( 2) B 1 s( 0.00%)p 1.00(100.00%)
8. (0.00000) RY*( 3) B 1 s( 0.00%)p 1.00(100.00%)
9. (0.00000) RY*( 4) B 1 s( 0.01%)p 1.00( 99.99%)
10. (0.00022) RY*( 1) H 2 s(100.00%)
0.0000 1.0000
11. (0.00016) RY*( 1) H 3 s(100.00%)
-0.0009 1.0000
12. (0.00022) RY*( 1) H 4 s(100.00%)
0.0000 1.0000
13. (0.01453) BD*( 1) B 1 - H 2
( 53.33%) 0.7303* B 1 s( 35.28%)p 1.83( 64.72%)
0.0000 0.5940 0.0035 0.0000 0.0000
0.7071 0.0048 0.3836 0.0021
( 46.67%) -0.6832* H 2 s(100.00%)
1.0000 0.0000
14. (0.01434) BD*( 1) B 1 - H 3
( 54.33%) 0.7371* B 1 s( 29.44%)p 2.40( 70.56%)
0.0000 0.5425 -0.0076 0.0000 0.0000
0.0000 0.0000 -0.8399 0.0099
( 45.67%) -0.6758* H 3 s(100.00%)
1.0000 0.0009
15. (0.01453) BD*( 1) B 1 - H 4
( 53.33%) 0.7303* B 1 s( 35.28%)p 1.83( 64.72%)
0.0000 0.5940 0.0035 0.0000 0.0000
-0.7071 -0.0048 0.3836 0.0021
( 46.67%) -0.6832* H 4 s(100.00%)
1.0000 0.0000
Looking at the second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis, which shows the mixing of bonding and non-bonding NBOs. There are no value of E2 greater than 20 kcal/mol so these value are not of interest for BH3.
Below is a natural bond orbitals summary taken from the log file, BD shows a bond, CR is the core and LP is a lone pair.
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3B)
1. BD ( 1) B 1 - H 2 1.98513 -0.40504 15(g),14(g)
2. BD ( 1) B 1 - H 3 1.98620 -0.37357 13(g),15(g)
3. BD ( 1) B 1 - H 4 1.98513 -0.40504 13(g),14(g)
4. CR ( 1) B 1 1.99953 -6.74894 10(v),12(v),11(v)
5. LP*( 1) B 1 0.00000 0.73770
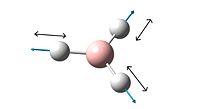
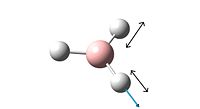
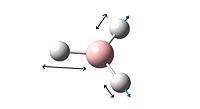
Vibrational Analysis
The vibrational analysis essentially provides us with the information about whether the structure found is the one with the lowest energy along the potential surface of the molecule. Here the energy of the structure is very close to the energy provided by the optimisation, this confirms that the frequency analysis is being performed on the minima found in the optimisation. The gradient here is very low, which again shows us that we have a structure which is at equilibrium with respect to the forces acting on the nuclei and the electrons in the optimised molecule.
E(RB3LYP) = -26.462 A.U.
RMS Gradient Norm = 0.00000081 A.U.
Final Dipole Moment - 0.00D
Full point group - C2v
Time taken to perform the calculation - 9 Minutes 46.0 seconds running on the laptop
Frequency analysis file: https://wiki.ch.ic.ac.uk/wiki/images/2/2f/CG507_BH3_FREQ.LOG
The low frequencies information provided in the log file is shown below. These are relatively small, with the largest value being about 24cm-1 which is an order of magnitude different to the vibrational frequencies of the molecule shown in table 2. These values are quite good, the better the method the closer these values would be to zero. As the basis set used here has a low accuracy these devaitions are acceptable. Every molecule has 3N-6 degrees of freedom, the low frequencies below are equivalent to the -6 and represent the vibrations of the centre of mass of the molecule.
Low frequencies --- -0.0001 0.0008 0.0008 9.6159 21.8113 24.9318
| Vibration (Hz) | |||||
|---|---|---|---|---|---|
| Vibration | Frequency | Intensity | Symmetry Label | Vibration Representation | Vibration Description |
| 1 | 1146 | 93 | a''2 |  |
Bending of bonds in the y plane |
| 2 | 1205 | 12 | e' |  |
Symmetrical bend of two B-H bonds towards each other |
| 3 | 1025 | 12 | e' |  |
Large bending in one B-H bond leading to a smaller bend in the other two B-H bonds |
| 4 | 2593 | 0 | a1' |  |
Symetrical stretch of each B-H bond |
| 5 | 2731 | 104 | e' |  |
Asymmetric stretch of two B-H bonds |
| 6 | 2731.41 | 104 | e' |  |
Asymetric stretch on one B-H bond with the symmetric stretch of the otrher two B-H bonds |
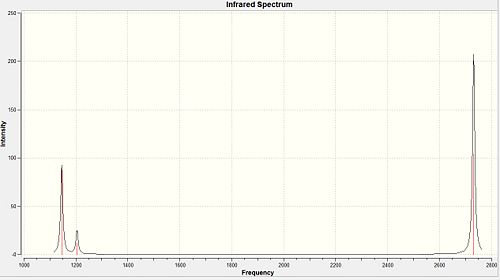
Although there are six different vibrations of the BH3 molecule only three can be seen on the vibrational spectrum. This is because one of the frequencies has zero intensity and four of the vibrations represent two degenerate vibrations with the same energy.
TlCl3
TlCl3 is restricted to the D3h point group with a very tight (0.0001) tolerance.
Data provided from Gaussian following the optimisation of the molecule:
4 atoms 186 electrons neutral singlet
All Tl-Cl Bond lengths - 2.65095
All Cl-Tl-Cl Bond angles - 120.0
The Gaussian optimisation of TlCl3 produces a Gaussian log file which can be viewed in Windows WordPad. This file contains all of the information recorded during the optimisation of the geometry. The method used for the optimisation was the DFT B3LYP method using a basis option of LanL2DZ, which uses a basis set of D95V on first row atoms and Los Alamos ECP on heavier elements.
E(RB3LYP) = -91.218 A.U.
Final Dipole Moment - 0.00D
Full point group - D3h
Time taken to perform the calculation - 36.0 seconds
Data file: https://wiki.ch.ic.ac.uk/wiki/images/a/ac/CG507TLBR3OPTIMISATION.LOG
Isomers of Mo(CO)4L2
Mo(CO)4L2 with cis PCl3 ligands
Optimisation
Optimisation using B3LYP method with a LANL2MB basis set:
P-Cl bond length - 2.38-2.41
Mo-4CO and Mo-8CO bond length - 2.11
Mo-6CO bond length - 2.06
Mo-2CO bond length - 2.06
4C-5O and 8C-9O bond length - 1.19
2C-3O bond length - 1.19
OC(8)-Mo-P(10)Cl3 - 90.5 degrees
OC(8)-Mo-P(11)Cl3 - 90.6 degrees
OC(8)-Mo-C(2)O - 89.4 degrees
OC(8)-Mo-C(6)O - 89.4 degrees
E(RB3LYP) = -617.525 A.U.
RMS Gradient Norm = 0.00007137
Final Dipole Moment - 8.46D
Full point group - C1
Time taken to perform the calculation - 12 minutes 0.3 seconds
Optimisation using B3LYP method with a LANL2DZ basis set:
P-Cl bond length - 2.24
Mo-4CO and Mo-8CO bond length - 2.06
Mo-6CO bond length - 2.01
Mo-2CO bond length - 2.01
4C-5O and 8C-9O bond length - 1.17311
2C-3O bond length - 1.18
6C-7O bond length - 1.18
OC(8)-Mo-P(10)Cl3 - 91.9 degrees
OC(8)-Mo-P(11)Cl3 - 89.2 degrees
OC(8)-Mo-C(2)O - 89.7 degrees
OC(8)-Mo-C(6)O - 89.0 degrees
E(RB3LYP) = -623.577 A.U.
RMS Gradient Norm = 0.00000674 A.U.
Final Dipole Moment - 1.31D
Full point group - C1
Time taken to perform the calculation - 1 hour 13 minutes 59.8 seconds
Vibrational Analysis
E(RB3LYP) = -623.577 A.U.
This energy is the same as it was after the optomisation, which shows that the frequency analysis was performed on the optimised structure. The freuency vibrations of the molecule are shown below, there are a significant number of vibrations which have a wide range. The low frequencies again are low and are acceptable according to the accuracy of the basis sets used.
Low frequencies --- 10.7714 17.6127 42.0442
1 2 3
A A A
Frequencies -- 10.7554 17.6127 42.0442
Red. masses -- 29.7744 32.3028 19.3502
Frc consts -- 0.0020 0.0059 0.0202
IR Inten -- 0.0264 0.0074 0.0048
4 5 6
A A A
Frequencies -- 44.4255 56.2325 66.6693
Red. masses -- 28.2290 22.6511 17.5929
Frc consts -- 0.0328 0.0422 0.0461
IR Inten -- 0.1031 0.8280 0.2247
7 8 9
A A A
Frequencies -- 78.3284 80.8584 86.2218
Red. masses -- 17.1873 19.5470 16.0789
Frc consts -- 0.0621 0.0753 0.0704
IR Inten -- 0.2444 0.4679 0.0202
10 11 12
A A A
Frequencies -- 92.6366 97.6337 97.9405
Red. masses -- 17.0912 27.5319 17.4471
Frc consts -- 0.0864 0.1546 0.0986
IR Inten -- 0.4118 0.0655 0.2571
13 14 15
A A A
Frequencies -- 99.0293 104.8135 121.4520
Red. masses -- 31.4054 30.4113 29.3502
Frc consts -- 0.1815 0.1968 0.2551
IR Inten -- 0.0062 0.0090 0.5493
16 17 18
A A A
Frequencies -- 139.1449 143.5332 165.4368
Red. masses -- 33.0940 34.7023 33.3622
Frc consts -- 0.3775 0.4212 0.5380
IR Inten -- 0.7351 1.3051 0.0004
19 20 21
A A A
Frequencies -- 169.8592 175.7353 177.4497
Red. masses -- 30.9316 30.2004 32.8765
Frc consts -- 0.5258 0.5495 0.6099
IR Inten -- 0.0658 0.7038 0.0018
22 23 24
A A A
Frequencies -- 234.9367 235.4936 378.0602
Red. masses -- 34.3045 34.1341 13.5558
Frc consts -- 1.1156 1.1153 1.1416
IR Inten -- 12.8279 28.8439 11.5247
25 26 27
A A A
Frequencies -- 378.8566 396.0039 396.2797
Red. masses -- 13.8988 29.8624 21.8964
Frc consts -- 1.1754 2.7591 2.0259
IR Inten -- 0.0065 14.0582 8.1903
28 29 30
A A A
Frequencies -- 404.9629 407.8574 410.3321
Red. masses -- 14.6500 22.3883 26.5652
Frc consts -- 1.4155 2.1943 2.6353
IR Inten -- 1.9246 273.8653 8.4184
31 32 33
A A A
Frequencies -- 418.9423 424.7174 431.7512
Red. masses -- 25.8037 17.6489 25.1808
Frc consts -- 2.6683 1.8757 2.7656
IR Inten -- 1.7115 76.5770 241.3770
34 35 36
A A A
Frequencies -- 436.8063 458.7829 465.4059
Red. masses -- 22.5535 19.9540 14.0111
Frc consts -- 2.5354 2.4745 1.7881
IR Inten -- 152.7106 45.7034 37.9366
37 38 39
A A A
Frequencies -- 514.1671 529.8076 563.7701
Red. masses -- 12.3710 12.3841 14.5702
Frc consts -- 1.9269 2.0481 2.7285
IR Inten -- 0.0187 0.2973 82.0179
40 41 42
A A A
Frequencies -- 580.0622 597.6333 1945.2876
Red. masses -- 14.4269 14.5885 13.3561
Frc consts -- 2.8600 3.0699 29.7782
IR Inten -- 92.7268 105.3136 762.7270
43 44 45
A A A
Frequencies -- 1948.6715 1958.3479 2023.3147
Red. masses -- 13.4083 13.3437 13.2993
Frc consts -- 29.9987 30.1513 32.0780
IR Inten -- 1498.5552 632.9485 597.6445
Computational Data - DOI:10042/to-7099
Mo(CO)4L2 with trans PCl3 ligands
Optimisation
Optimisation using B3LYP method with a LANL2MB basis set:
Mo-P bond length - 2.48
P-Cl bond length - 2.40
All Mo-CO bond lengths - 2.11
All C-O bond lengths - 1.19
OC(6)-Mo-P(10)Cl3 - 90.6 degrees
OC(6)-Mo-P(11)Cl3 - 89.4 degrees
OC(4)-Mo-C(6)O - 90.0 degrees
OC(8)-Mo-C(6)O - 90.0 degrees
OC(6)-Mo-C(2)O - 180.0 degrees
E(RB3LYP) = -617.522 A.U.
RMS Gradient Norm = 0.00002926
Final Dipole Moment - 0.00D
Full point group - C1
Time taken to perform the calculation - 12 minutes 27.8 seconds
Optimisation using B3LYP method with a LANL2DZ basis set:
Mo-P bond length - 2.44
P-Cl bond length - 2.24
All Mo-CO bond lengths - 2.06
All C-O bond lengths - 1.17
OC(6)-Mo-P(10)Cl3 - 90.0 degrees
OC(6)-Mo-P(11)Cl3 - 90.0 degrees
OC(4)-Mo-C(6)O - 89.5 degrees
OC(6)-Mo-C(8)O - 90.5 degrees
OC(6)-Mo-C(2)O - 179.0 degrees
E(RB3LYP) = -623.576 A.U.
RMS Gradient Norm = 0.00002669 A.U.
Final Dipole Moment - 0.31D
Full point group - C1
Time taken to perform the calculation - 47 minutes 37.8 seconds
Vibrational Analysis
E(RB3LYP) = -623.576 A.U.
Low frequencies --- -2.2041 -1.5955 -0.0005 -0.0004 -0.0002 3.1836
Low frequencies --- 5.1569 6.2087 37.2059
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A A A
Frequencies -- 4.9748 6.1192 37.2059
Red. masses -- 21.7857 34.6922 27.0464
Frc consts -- 0.0003 0.0008 0.0221
IR Inten -- 0.0942 0.0000 0.4188
4 5 6
A A A
Frequencies -- 40.2209 72.2572 78.5677
Red. masses -- 25.6605 17.9513 18.7887
Frc consts -- 0.0245 0.0552 0.0683
IR Inten -- 0.3117 0.0001 1.0692
7 8 9
A A A
Frequencies -- 79.0896 80.1138 83.3308
Red. masses -- 18.8183 18.6272 15.8696
Frc consts -- 0.0694 0.0704 0.0649
IR Inten -- 0.0000 1.0951 0.0010
10 11 12
A A A
Frequencies -- 88.2910 96.8673 102.4355
Red. masses -- 15.5400 18.0557 27.9601
Frc consts -- 0.0714 0.0998 0.1729
IR Inten -- 0.0015 0.0277 0.0000
13 14 15
A A A
Frequencies -- 103.0671 109.9741 123.2401
Red. masses -- 27.6830 34.5586 31.4486
Frc consts -- 0.1733 0.2463 0.2814
IR Inten -- 0.0000 0.0093 0.4328
16 17 18
A A A
Frequencies -- 125.3156 161.2164 162.6660
Red. masses -- 31.6855 32.6745 32.7364
Frc consts -- 0.2932 0.5004 0.5104
IR Inten -- 0.3862 0.0000 0.0617
19 20 21
A A A
Frequencies -- 171.7341 190.3831 190.6131
Red. masses -- 38.6637 29.9782 30.1132
Frc consts -- 0.6718 0.6402 0.6446
IR Inten -- 6.4577 0.7522 0.7996
22 23 24
A A A
Frequencies -- 240.2024 251.7645 346.2552
Red. masses -- 34.1247 36.9295 12.7408
Frc consts -- 1.1600 1.3792 0.9000
IR Inten -- 0.0423 37.6065 0.0040
25 26 27
A A A
Frequencies -- 388.6203 388.6493 389.3980
Red. masses -- 17.7757 20.2990 22.0099
Frc consts -- 1.5817 1.8065 1.9663
IR Inten -- 0.0003 1.5460 0.417
28 29 30
A A A
Frequencies -- 389.5998 401.3300 406.8777
Red. masses -- 17.3110 14.9410 14.7808
Frc consts -- 1.5481 1.4179 1.4417
IR Inten -- 1.7147 3.9015 0.0403
31 32 33
A A A
Frequencies -- 408.8037 423.2874 425.6021
Red. masses -- 32.1788 25.2383 25.1027
Frc consts -- 3.1685 2.6643 2.6790
IR Inten -- 727.6780 168.4655 166.0350
34 35 36
A A A
Frequencies -- 436.3571 436.4767 457.8912
Red. masses -- 18.3450 18.9320 29.1137
Frc consts -- 2.0580 2.1250 3.5964
IR Inten -- 0.0062 6.0490 0.0819
37 38 39
A A A
Frequencies -- 483.2778 523.0843 574.1329
Red. masses -- 12.3169 12.3784 14.3917
Frc consts -- 1.6949 1.9955 2.7950
IR Inten -- 0.0019 0.0097 87.8634
40 41 42
A A A
Frequencies -- 574.3130 603.5716 1950.4374
Red. masses -- 14.4070 14.1952 13.4113
Frc consts -- 2.7998 3.0468 30.0598
IR Inten -- 89.8693 138.3486 1475.4337
43 44 45
A A A
Frequencies -- 1951.0768 1977.3502 2031.1315
Red. masses -- 13.4126 13.3318 13.2971
Frc consts -- 30.0824 30.7118 32.3209
IR Inten -- 1466.7554 0.6378 3.7698
Computational Data - DOI:10042/to-7100
The energy of the optimised cis and trans structure is the same, this would suggest that there is an equilibrium between the two isomers as they both have the same energy and conversion to the other isomer would readily occur.
Mini Project
In this mini project involves the study of metal containing diatomic compounds. These diatomics differ to simple diatomics due to the inclusion of d-orbitals. As we are using a large gold containing diatomic a pseudo-potential was used in the Gaussian calculations. The B3LYP method was used and a 6-311G(d,p) basis set was used for the oxygen and the sulphur and a LANL2DZ pseudo-potential was used for the gold. 6-311G(d,p)
Optimisation
AuS-
Data provided from Gaussian following the optimisation of the molecule:
2 atoms -1 Charge singlet
Bond lengths - 2.29
The Gaussian optimisation of BH3 produces a Gaussian log file which can be viewed in Windows WordPad. This file contains all of the information recorded during the optimisation of the geometry.
E(RB3LYP) = -533.742 A.U.
RMS Gradient Norm - 0.00003038 A.U.
Final Dipole Moment - 6.3D
Full point group - C*V
Time taken to perform the calculation - 30.03 seconds
From literature the AuS bond was reported to be 2.331Å using a B3PW91/LANL2DZ optimisation and 2.240Å using a B3PW91/LANL-E method and basis set DOI:10.1021/ja982234c
AuO-
Data provided from Gaussian following the optimisation of the molecule:
2 atoms -1 charge singlet
Bond length - 1.90
The Gaussian optimisation of BH3 produces a Gaussian log file which can be viewed in Windows WordPad. This file contains all of the information recorded during the optimisation of the geometry.
E(RB3LYP) = -210.668 A.U.
RMS Gradient Norm - 0.00000321 A.U.
Final Dipole Moment - 3.96D
Full point group - C*V
Time taken to perform the calculation - 27.6 seconds
From literature the AuO bond length from an Au2O complex was reported as 1.96-1.99Å using a (BO-LSD-MD) method,DOI:10.1021/jp027596s . In another article 1.946Å was reported using a B3PW91/LANL2DZ optimisation and 1.925 using a B3PW91/LANL-E method and basis set DOI:10.1021/ja982234c
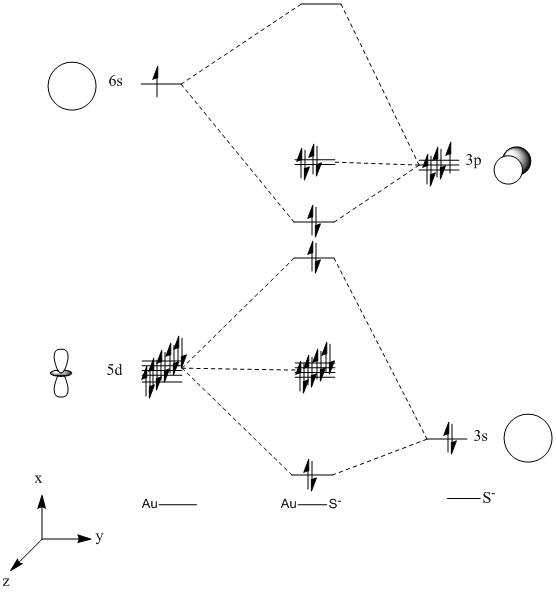
Molecular Orbital Analysis
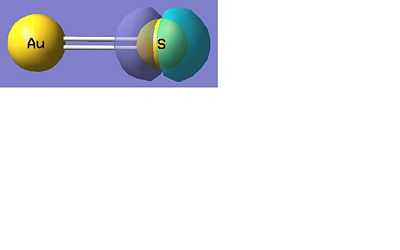
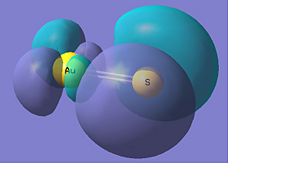
AuS-
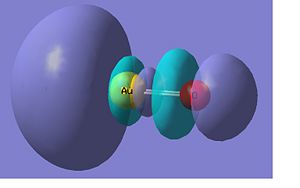
Below there is a molecular orbital diagram of AuS- which shows the valence orbitals and the valence electrons. The only atomic orbitals shown are the sigma+ atomic orbitals of each atom. These are shown as they are the only atomic orbitals where the symmetry matches. The combination of the S- and the Au results in lots of non bonding orbitals as core or lone pairs, which are also shown in the natural bond analysis formed as there is no atomic orbital of similar energy on the other fragment orbital of the same symmetry. The bonding and antibonding orbitals formed also have the same symmetry as the atomic orbitals that were combined to form the molecular orbitals. The LUMO should be made up of a p contribution from the sulphur and a s like character from the gold. This type of molecular orbital is shown in the molecular orbital representation shown below from the Gaussian calculation. From my predicted MO diagram I would expect the HOMO and the HOMO-1 to be the non bonding p orbitals (x and y) from the sulphur atom, the Gaussian calculation shows that these are degenerate as they have the same energy. In the representations shown below this is the case, though there is a small d-orbital contribution from the gold atom in this case. The low lying molecular orbitals a centred around the sulphur atom, which must have the atomic orbitals with the lowest energy.
There are 18 occupied molecular orbitals in AuS-, the three orbitals lowest in energy, the HOMO-1, HOMO, LUMO and LUMO+1 are shown below.
| Molecular Orbital Analysis | |||
|---|---|---|---|
| Molecular Orbital | MO Representation | Energy (kcal/mol) | Occupied? |
| 1 |  |
-88.617 | Yes |
| 2 |  |
-7.700 | Yes |
| 3 |  |
-5.667 | Yes |
| 17 |  |
-0.017 | Yes |
| 18 |  |
-0.017 | Yes |
| 19 |  |
0.058 | No |
| 20 |  |
0.138 | No |
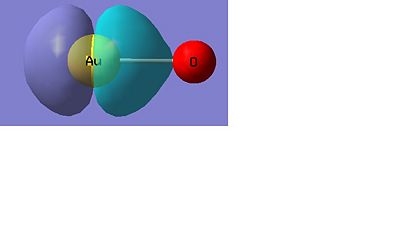
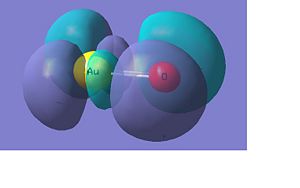
AuO-
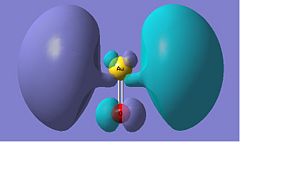
Below there is a molecular orbital diagram of AuO- which shows the valence orbitals and the valence electrons. The HOMO and LUMO is the same as for the sulphur as predicted. Though in this case there is a lower contribution to the molecular orbital from the oxygen than there was from the sulphur. The only atomic orbitals shown are the sigma+ atomic orbitals of each atom. These are shown as they are the only atomic orbitals where the symmetry matches to an atomic orbital on the other fragment orbital. The combination of the O- and the Au results in lots of non bonding orbitals as core or lone pairs, which are also shown in the natural bond analysis. The bonding and antibonding orbitals formed also have the same symmetry as the atomic orbitals that were combined to form the molecular orbitals.
There are 14 occupied molecular orbitals in AuO-, the three orbitals lowest in energy, the HOMO-1, HOMO, LUMO and LUMO+1 are shown below.
| Molecular Orbital Analysis | |||
|---|---|---|---|
| Molecular Orbital | MO Representation | Energy (kcal/mol) | Occupied? |
| 1 |  |
-18.865 | Yes |
| 2 |  |
-3.976 | Yes |
| 3 |  |
-2.124 | Yes |
| 13 HOMO-1 |  |
-0.007 | Yes |
| 14 HOMO |  |
-0.007 | Yes |
| 15 LUMO |  |
0.091 | No |
| 16 LUMO+1 |  |
0.150 | No |
NBO Analysis
AuS-
Atoms coloured by charge, bright red shows a highly negative charge, The highly negatively charged Sulphur atom is bright red and the Gold atom is also negative.
NBO Charges:
Au = -0.309 S = -0.691
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
S 1 -0.95866 9.99987 6.94467 0.01412 16.95866
Au 2 -0.04134 67.99551 11.04328 0.00255 79.04134
=======================================================================
* Total * -1.00000 77.99538 17.98795 0.01667 96.00000
The natural bond orbital analysis (below) shows that there is only one bond between the gold and the sulphur atoms. The S atom contributes 53.0% to the bond and the Au contributes the other 47.0% of the bond. The hybridisation of the sulphur bonding orbital includes a s, p and d contribution, though there is a dominant p character.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (2.00000) BD ( 1) S 1 -Au 2
( 52.96%) 0.7277* S 1 s( 4.95%)p19.16( 94.77%)d 0.06( 0.29%)
0.0000 0.0000 0.2188 0.0399 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.9733 -0.0172 -0.0010
0.0000 0.0000 0.0000 0.0000 0.0000
0.0537
( 47.04%) 0.6859*Au 2 s( 84.00%)p 0.00( 0.32%)d 0.19( 15.68%)
0.0000 0.9164 0.0137 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0425 0.0371 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.3960 -0.0027
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis, there are no value of E2 greater than 20 kcal/mol so these value are not of interest.
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1 1. BD ( 1) S 1 -Au 2 / 21. LP*( 8)Au 2 1.13 0.46 0.021 2. CR ( 1) S 1 / 21. LP*( 8)Au 2 0.61 87.74 0.208 3. CR ( 2) S 1 / 21. LP*( 8)Au 2 4.67 8.83 0.183 10. CR ( 4)Au 2 / 48. BD*( 1) S 1 -Au 2 6.11 2.26 0.105 11. LP ( 1) S 1 / 21. LP*( 8)Au 2 15.84 0.82 0.102 12. LP ( 2) S 1 / 19. LP*( 6)Au 2 5.62 0.20 0.030 13. LP ( 3) S 1 / 20. LP*( 7)Au 2 5.62 0.20 0.030 16. LP ( 3)Au 2 / 23. RY*( 2) S 1 1.24 0.86 0.029 17. LP ( 4)Au 2 / 24. RY*( 3) S 1 1.24 0.86 0.029 18. LP ( 5)Au 2 / 22. RY*( 1) S 1 2.00 0.87 0.037
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (SAu)
1. BD ( 1) S 1 -Au 2 2.00000 -0.22572 21(g)
2. CR ( 1) S 1 2.00000 -87.50250 21(v)
3. CR ( 2) S 1 1.99991 -8.59064 21(v)
4. CR ( 3) S 1 2.00000 -5.65552
5. CR ( 4) S 1 2.00000 -5.65552
6. CR ( 5) S 1 1.99996 -5.66615
7. CR ( 1)Au 2 1.99984 -3.94491
8. CR ( 2)Au 2 1.99999 -2.11158
9. CR ( 3)Au 2 1.99999 -2.11158
10. CR ( 4)Au 2 1.99568 -2.12699 48(g)
11. LP ( 1) S 1 1.97339 -0.58565 21(v)
12. LP ( 2) S 1 1.95790 -0.02483 19(v)
13. LP ( 3) S 1 1.95790 -0.02483 20(v)
14. LP ( 1)Au 2 1.99994 -0.12096
15. LP ( 2)Au 2 1.99994 -0.12096
16. LP ( 3)Au 2 1.99769 -0.14028 23(v)
17. LP ( 4)Au 2 1.99769 -0.14028 24(v)
18. LP ( 5)Au 2 1.99655 -0.13589 22(v)
19. LP*( 6)Au 2 0.04210 0.17364
20. LP*( 7)Au 2 0.04210 0.17364
21. LP*( 8)Au 2 0.02669 0.23908
22. RY*( 1) S 1 0.00357 0.73102
23. RY*( 2) S 1 0.00231 0.71545
24. RY*( 3) S 1 0.00231 0.71545
25. RY*( 4) S 1 0.00006 1.02938
26. RY*( 5) S 1 0.00006 1.02937
27. RY*( 6) S 1 0.00005 0.98593
28. RY*( 7) S 1 0.00000 15.65001
29. RY*( 8) S 1 0.00000 1.72143
30. RY*( 9) S 1 0.00000 17.42693
31. RY*( 10) S 1 0.00000 181.10384
32. RY*( 11) S 1 0.00001 1.84697
33. RY*( 12) S 1 0.00000 17.37211
34. RY*( 13) S 1 0.00000 0.84300
35. RY*( 14) S 1 0.00001 0.81479
36. RY*( 15) S 1 0.00001 0.81479
37. RY*( 16) S 1 0.00000 1.72143
38. RY*( 17) S 1 0.00000 17.42693
39. RY*( 1)Au 2 0.00003 2.21141
40. RY*( 2)Au 2 0.00002 0.77862
41. RY*( 3)Au 2 0.00000 0.24398
42. RY*( 4)Au 2 0.00000 0.91321
43. RY*( 5)Au 2 0.00000 0.54046
44. RY*( 6)Au 2 0.00000 0.59277
45. RY*( 7)Au 2 0.00000 0.59277
46. RY*( 8)Au 2 0.00000 0.54035
47. RY*( 9)Au 2 0.00000 0.24398
48. BD*( 1) S 1 -Au 2 0.00428 0.13404
-------------------------------
Total Lewis 95.87639 ( 99.8712%)
Valence non-Lewis 0.11518 ( 0.1200%)
Rydberg non-Lewis 0.00843 ( 0.0088%)
-------------------------------
Total unit 1 96.00000 (100.0000%)
Charge unit 1 -1.00000
AuO-
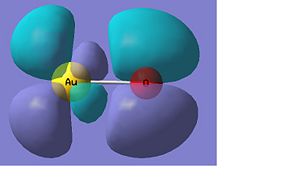
Atoms here are coloured by charge, bright red shows a highly negative charge, The highly negatively charged Oxygen atom is bright red and the Gold atom is also negative.
NBO Charges:
Au = -0.333 O = -0.667
Summary of Natural Population Analysis, this shows the charges of each atom provided in the Gaussian log file:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
O 1 -0.80427 1.99998 6.79951 0.00478 8.80427
Au 2 -0.19573 67.99176 11.19622 0.00775 79.19573
=======================================================================
* Total * -1.00000 69.99174 17.99573 0.01253 88.00000
Natural Population -------------------------------------------------------- Effective Core 60.00000 Core 9.99174 ( 99.9174% of 10) Valence 17.99573 ( 99.9763% of 18) Natural Minimal Basis 87.98747 ( 99.9858% of 88) Natural Rydberg Basis 0.01253 ( 0.0142% of 88) --------------------------------------------------------
Below the contributions of each atom to the bonding orbital can be seen and the hybridisations are also shown. For this molecule it can be seen that there are three bonds between the Au and the O atoms. In each case there is a majority contribution from the oxgen atom towards the bonding orbital, this is reflected by the high electron density located on the oxygen atom. In each case the bonding orbital has almost exclusively p character, which can also be seen in the molecular orbitals around the HOMO in the molecule. This suggests that the bonding in AuO- is more like a triple bond that the single bond character shown in AuS-. This is also reflected in the lengths of the bonds, with the former being significantly shorter than the latter.
---------------------------------------------------------------------------------
1. (2.00000) BD ( 1) O 1 -Au 2
( 94.56%) 0.9724* O 1 s( 0.00%)p 1.00( 99.99%)d 0.00( 0.01%)
0.0000 0.0000 0.0000 0.0000 0.9999
-0.0041 -0.0009 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0099
0.0000 0.0000 0.0000
( 5.44%) 0.2333*Au 2 s( 0.00%)p 1.00( 98.49%)d 0.02( 1.51%)
0.0000 0.0000 0.0000 0.0000 0.9924
0.0112 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 -0.1022
-0.0683 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000
2. (2.00000) BD ( 2) O 1 -Au 2
( 94.56%) 0.9724* O 1 s( 0.00%)p 1.00( 99.99%)d 0.00( 0.01%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.9999 -0.0041 -0.0009
0.0000 0.0000 0.0000 0.0000 0.0000
0.0099 0.0000 0.0000
( 5.44%) 0.2333*Au 2 s( 0.00%)p 1.00( 98.49%)d 0.02( 1.51%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.9924 0.0112 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 -0.1022 -0.0683 0.0000 0.0000
0.0000 0.0000
3. (2.00000) BD ( 3) O 1 -Au 2
( 52.25%) 0.7228* O 1 s( 3.40%)p28.41( 96.55%)d 0.02( 0.06%)
0.0000 0.1824 0.0267 -0.0003 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.9825 0.0151 0.0021 0.0000 0.0000
0.0000 0.0000 0.0236
( 47.75%) 0.6910*Au 2 s( 59.55%)p 0.03( 1.78%)d 0.65( 38.67%)
0.0000 0.7713 0.0248 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.1327 0.0130 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.6182 -0.0679
The second order perturbation theory analysis of Fock Matrix in NBO Basis shows that the values again show no important information about the equilibrium structure of the molecule.
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1 3. BD ( 3) O 1 -Au 2 / 15. LP*( 6)Au 2 1.60 0.55 0.027 4. CR ( 1) O 1 / 15. LP*( 6)Au 2 2.81 19.03 0.208 8. CR ( 4)Au 2 / 40. BD*( 3) O 1 -Au 2 11.65 2.26 0.145 9. LP ( 1) O 1 / 15. LP*( 6)Au 2 19.93 1.02 0.127 9. LP ( 1) O 1 / 31. RY*( 3)Au 2 0.56 3.67 0.041 12. LP ( 3)Au 2 / 17. RY*( 2) O 1 0.67 1.43 0.028 13. LP ( 4)Au 2 / 18. RY*( 3) O 1 0.67 1.43 0.028 14. LP ( 5)Au 2 / 16. RY*( 1) O 1 1.14 1.61 0.038
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (OAu)
1. BD ( 1) O 1 -Au 2 2.00000 -0.03393
2. BD ( 2) O 1 -Au 2 2.00000 -0.03393
3. BD ( 3) O 1 -Au 2 2.00000 -0.23288 15(g)
4. CR ( 1) O 1 1.99998 -18.70725 15(v)
5. CR ( 1)Au 2 1.99991 -3.94872
6. CR ( 2)Au 2 1.99999 -2.09556
7. CR ( 3)Au 2 1.99999 -2.09556
8. CR ( 4)Au 2 1.99186 -2.10940 40(g)
9. LP ( 1) O 1 1.97051 -0.69904 15(v),31(v)
10. LP ( 1)Au 2 1.99999 -0.09987
11. LP ( 2)Au 2 1.99999 -0.09999
12. LP ( 3)Au 2 1.99925 -0.11729 17(v)
13. LP ( 4)Au 2 1.99925 -0.11729 18(v)
14. LP ( 5)Au 2 1.99890 -0.09220 16(v)
15. LP*( 6)Au 2 0.02960 0.31913
16. RY*( 1) O 1 0.00111 1.51642
17. RY*( 2) O 1 0.00075 1.31147
18. RY*( 3) O 1 0.00075 1.31147
19. RY*( 4) O 1 0.00000 5.03662
20. RY*( 5) O 1 0.00000 49.87680
21. RY*( 6) O 1 0.00000 5.03662
22. RY*( 7) O 1 0.00000 1.41651
23. RY*( 8) O 1 0.00000 4.99422
24. RY*( 9) O 1 0.00001 3.10744
25. RY*( 10) O 1 0.00000 2.85256
26. RY*( 11) O 1 0.00000 2.85256
27. RY*( 12) O 1 0.00001 3.10744
28. RY*( 13) O 1 0.00000 3.00932
29. RY*( 1)Au 2 0.00001 0.62505
30. RY*( 2)Au 2 0.00000 0.26549
31. RY*( 3)Au 2 0.00000 2.97572
32. RY*( 4)Au 2 0.00001 0.39615
33. RY*( 5)Au 2 0.00000 0.56115
34. RY*( 6)Au 2 0.00000 0.68587
35. RY*( 7)Au 2 0.00000 0.68587
36. RY*( 8)Au 2 0.00000 0.56111
37. RY*( 9)Au 2 0.00000 0.26549
38. BD*( 1) O 1 -Au 2 0.00000 0.19036
39. BD*( 2) O 1 -Au 2 0.00000 0.19036
40. BD*( 3) O 1 -Au 2 0.00808 0.14957
-------------------------------
Total Lewis 87.95965 ( 99.9541%)
Valence non-Lewis 0.03768 ( 0.0428%)
Rydberg non-Lewis 0.00267 ( 0.0030%)
-------------------------------
Total unit 1 88.00000 (100.0000%)
Charge unit 1 -1.00000
Vibrational Analysis
AuS-
E(RB3LYP) = -533.742 A.U.
The vibrational analysis taken from the Gaussian log file can be seen below, it contains one molecular vibration of 334.0 cm-1. Only one vibration would be expected here as the molecule is a linear diatomic molecule. There are only five low frequencies here as there are only 3N-5 degrees of freedom for a linear molecule.
Low frequencies --- -6.4919 -6.4919 -0.0014 -0.0013 0.0014 333.9450
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1
SG
Frequencies -- 333.9450
Red. masses -- 36.2078
Frc consts -- 2.3790
IR Inten -- 8.9621
Atom AN X Y Z
1 16 0.00 0.00 0.99
2 79 0.00 0.00 -0.16
AuO-
E(RB3LYP) = -210.668 A.U.
Low frequencies --- -73.0324 -73.0324 -0.0003 -0.0003 0.0002 623.7090
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1
SG
Frequencies -- 623.7090
Red. masses -- 17.1805
Frc consts -- 3.9378
IR Inten -- 28.9418
Atom AN X Y Z
1 8 0.00 0.00 1.00
2 79 0.00 0.00 -0.08
Files from the mini project:
AuS Optimisation - DOI:10042/to-7086
AuO Optimisation - DOI:10042/to-7085
AuS Frequency Analysis - DOI:10042/to-7083
AuO Frequency Analysis - DOI:10042/to-7084
AuO MO and NBO Analysis - DOI:10042/to-7088
AuS MO and NBO Analysis - DOI:10042/to-7087