Rep:Mod:21comlab
NH3 molecule
NH3 optimisation
NH3 optimisation
Calculation Method B3LYP
Basis Set 6-31G(d,p)
E(B3LYP) -56.55776873 a.u.
RMS Gradient Norm 0.00000485 a.u.
Point Group C3V
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986274D-10
NH3 bonds and angles details
N-H bond distance (Angstrom)= 1.01798
H-N-H bond angle (Degree)= 105.741
NH3 3D simulation
NH3 molecule |
LOG file link: [1]
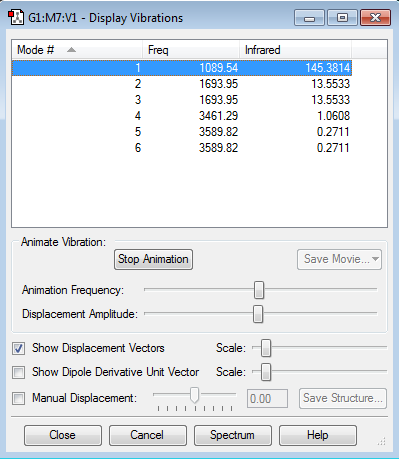
NH3 vibrations and frequencies
Questions and Answers
1-How many modes do you expect from the 3N-6 rule?
N=4, so the expected number of modes would be 12-6=6.
2-Which modes are degenerate (ie have the same energy)?
Modes number 2 and 3. Also, Modes number 5 and 6.
3-Which modes are "bending" vibrations and which are "bond stretch" vibrations?
"Bending" vibrations: modes number 1, 2, and 3.
"Bond stretch" vibrations: modes number 4, 5, and 6.
4-Which mode is highly symmetric?
The first mode is highly symmetric.
5-One mode is known as the "umbrella" mode, which one is this?
The first mode is the "umbrella" mode.
6-How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
I would expect to see 2 bands in an experimental spectrum of gaseous ammonia. The bands correspond to modes number 1, 2(3). There are also other frequencies which have infrared peaks, but they are too low in intensity, so we do not consider them as bands.
Charges on atoms in NH3
Charge on the N-atom(C) = -1.125
Charge on the H-atoms(C) = 0.375
Nitrogen is more electronegative than hydrogen, so it pulls the bonding electrons towards itself, and as a result carries a partial negative charge. Thus, the hydrogen atoms become partial positive charge carriers.
H2 and N2 molecules
H2 optimisation
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
H2 optimisation
Calculation Method B3LYP
Basis Set 6-31G(d,p)
E(B3LYP) -1.17853936 a.u.
RMS Gradient Norm 0.00000017 a.u.
Point Group D*H
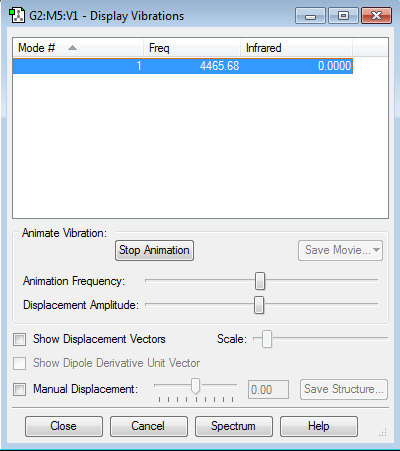
H2 vibrations and frequencies
H2 3D simulation
H2 ion |
LOG file link: [2]
N2 optimisation
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401061D-13
N2 optimisation
Calculation Method B3LYP
Basis Set 6-31G(d,p)
E(B3LYP) -109.52412868 a.u.
RMS Gradient Norm 0.00000060 a.u.
Point Group D*H
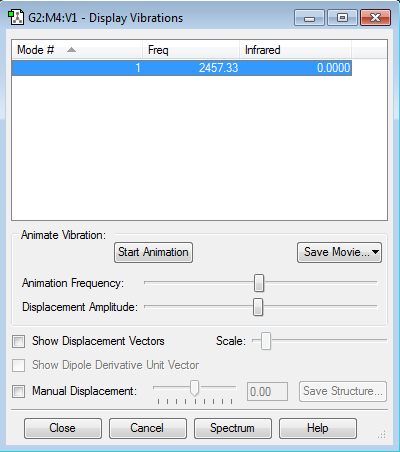
N2 vibrations and frequencies
N2 3D simulation
N2 ion |
LOG file link: [3]
Haber-Bosch reaction energy calculation
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u.
The energy for converting hydrogen and nitrogen gas into ammonia gas(ΔE) = -146.47849401 kJ/mol
Hence, the ammonia product is more stable than gaseous reactants.
Project molecule
CN- was chosen as the project molecule.
Calculations and details below all relate to this ion.
Basic info
C-N bond length(Angstrom) = 1.18409
Charge on C atom(C) = -0.754
charge on N atom(C) = -0.246
CN- optimisation
CN- optimisation
Calculation Method B3LYP
Basis Set 6-31G(d,p)
Charge -1
E(B3LYP) -92.82453153 a.u.
RMS Gradient Norm 0.00000704 a.u.
Point Group C*V
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000005 0.001800 YES
RMS Displacement 0.000008 0.001200 YES
Predicted change in Energy=-6.650393D-11
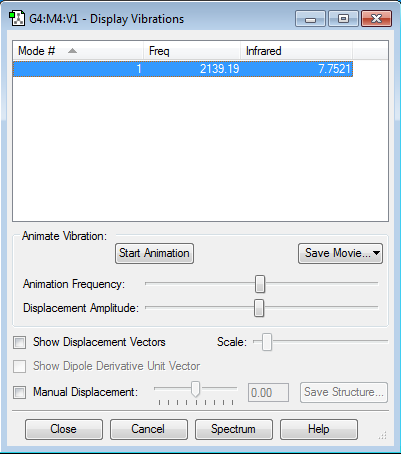
CN- vibrations and frequencies
CN- 3D simulation
CN- ion |
LOG file link: [4]
CN- selected MOs and description
Here are 6 selected MOs within CN- ion. Every MO is accompanied by a short description on its properties and characteristics.
Gray atom is the representative of carbon and the blue one corresponds to nitrogen.
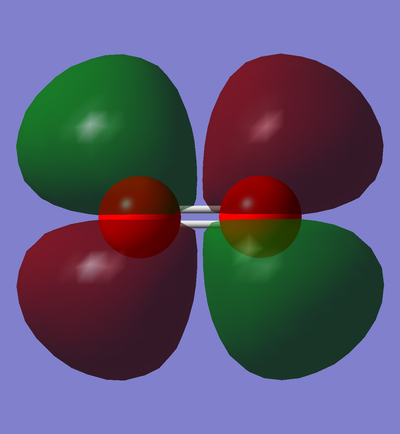
In phase overlap between 2s AOs
This is the transparent view of the occupied in phase overlap between 2s AO of carbon and 2s AO of nitrogen. As nitrogen is lower in energy than carbon, its AOs are also lower in energy than their equivalent AOs in carbon atom. Therefore, the contribution of 2s AO of nitrogen is larger, and as a result, the MO distribution is closer to the nitrogen atom rather than the carbon atom. This MO is bonding sigma orbital, but its bonding effects is cancelled out by the occupation of its corresponding sigma antibonding orbital.
Furthermore, this MO is so deep in energy in HOMO region( E= -0.56195 a.u.) .
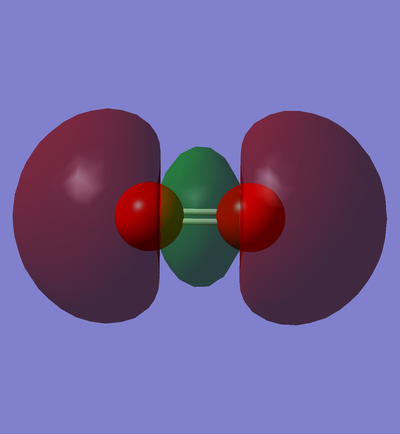
Out of phase overlap between 2s AOs
This is the transparent view of the occupied out of phase overlap between 2s AO of carbon and 2s AO of nitrogen. As carbon is higher in energy than carbon, its AOs are also higher in energy than their equivalent AOs in nitrogen atom. Therefore, the contribution of 2s AO of carbon is larger in antibonding MOs, and as a result, the MO distribution is closer to the carbon atom rather than the nitrogen atom. This MO is antibonding sigma orbital and it cancels out the bonding effect of its related bonding MO as was mentioned above.
Moreover, this MO is deep in energy in the HOMO region( E= -0.10626 a.u.) , although it is energetically higher than its corresponding bonding MO.
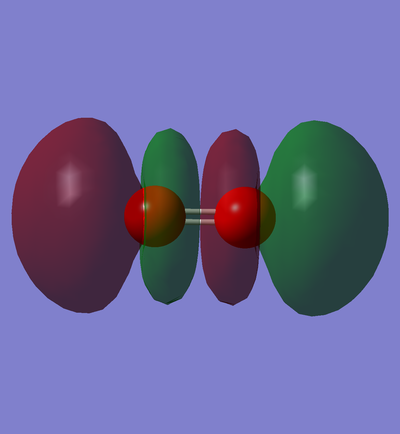
In phase overlap between 2px or 2py AOs
This is the transparent view of the occupied in phase overlap between 2px or 2py AO of carbon and 2px or 2py AO of nitrogen. As nitrogen is lower in energy than carbon, its AOs are also lower in energy than their equivalent AOs in carbon atom. Therefore, the contribution of 2s AO of nitrogen is larger, and as a result, the MO distribution is slightly closer to the nitrogen atom rather than the carbon atom, even though it is not properly illustrated above. This MO is bonding pi orbital, and the overlap between two p orbitals is side-on; thus, it causes a double bond between nitrogen and carbon. There are two double bonds present in cyanide ion and they are perpendicular to each other.
Besides, this MO is classified as a high MO in energy( E= -0.01696 a.u.) in comparison with other MOs in the HOMO region.
Out of phase overlap between 2px or 2py AOs
This is the transparent view of the unoccupied out of phase overlap between 2px or 2py AO of carbon and 2px or 2py AO of nitrogen. As carbon is higher in energy than carbon, its AOs are also higher in energy than their equivalent AOs in nitrogen atom. Therefore, the contribution of 2s AO of carbon is larger in antibonding MOs, and as a result, the MO distribution is closer to the carbon atom rather than the nitrogen atom. This MO is antibonding pi orbital, and becuase it has not been occupied, the pi bonds remain unchanged.
It is important to say that this MO is totally high in energy but energetically, is the lowest unoccupied MO in LUMO region( E= -0.35435 a.u.) .
In phase overlap between 2pz AOs
This is the transparent view of the occupied in phase overlap between 2pz AO of carbon and 2pz AO of nitrogen. As nitrogen is lower in energy than carbon, its AOs are also lower in energy than their equivalent AOs in carbon atom. Therefore, the contribution of 2s AO of nitrogen is larger, and as a result, the MO distribution is slightly closer to the nitrogen atom rather than the carbon atom. This MO is bonding sigma orbital because the overlap between p orbitals is end-on.
This MO is the the highest in the energy in the HOMO region( E= 0.01857 a.u.) .
Out of phase overlap between 2pz AOs
This is the mesh view of the unoccupied out of phase overlap between 2pz AO of carbon and 2pz AO of nitrogen. As carbon is higher in energy than carbon, its AOs are also higher in energy than their equivalent AOs in nitrogen atom. Therefore, the contribution of 2s AO of carbon is larger in antibonding MOs, and as a result, the MO distribution is closer to the carbon atom rather than the nitrogen atom. THis MO is antibonding sigma orbital, and because it has not occupied, it does not affect the bonding sigma orbital caused by in phase overlap between 2pz AOs.
Furthermore, this MO is energetically very high in the LUMO region( E= 0.59206 a.u.).
Analysis on O2 molecule
The O2 was chosen as another molecule to be analysed. In this part, the MOs of the molecule are also involved with a small description on their type and properties.
Basic info
Charge on O atoms within the molecule(C) : 0
O-O bond length(Angstrom) : 1.21461
O2 optimisation
O2 optimisation
Calculation Method UB3LYP
Basis Set 6-31G(d,p)
Spin Triplet
E(UB3LYP) -150.32004019 a.u.
RMS Gradient Norm 0.00006587 a.u.
Point Group D*H
Item Value Threshold Converged?
Maximum Force 0.000114 0.000450 YES
RMS Force 0.000114 0.000300 YES
Maximum Displacement 0.000069 0.001800 YES
RMS Displacement 0.000097 0.001200 YES
Predicted change in Energy=-7.817746D-09
O2 vibrations and frequencies
O2 3D simulation
Oxygen molecule |
LOG file link: [5]
O2 selected MOs and description
Here are 4 selected MOs within O2 ion. Every MO is accompanied by a short description on its properties and characteristics.
In phase overlap between 2px AOs
This is the transparent view of the occupied in phase overlap between either 2px or 2py AOs.
This MO is bonding pi orbital, and the overlap between two p orbitals is side-on; thus, it causes a double bond.
Besides, this MO is classified as an approximately high MO in energy( E= -0.54741 a.u.) in comparison with other MOs in the HOMO region.
Out of phase phase overlap between 2px AOs
This is the transparent view of the singly occupied out of phase overlap between either 2px or 2py AOs.
This MO is antibonding pi orbital, and becuase it has one electron, the pi bond decreases into its half order.
It is important to say that this MO is totally the highest in energy in the HOMO region( E= -0.30818 a.u.) .
In phase overlap between 2pz AOs
This is the transparent view of the occupied in phase overlap between 2pz AOs.
This MO is bonding sigma orbital because the overlap between p orbitals is end-on, although it has also antibonding character.
This MO is slightly high in the energy in the HOMO region( E= -0.55938 a.u.) .
Out of phase phase overlap between 2pz AOs
This is the transparent view of the unoccupied out of phase overlap between 2pz AOs.
THis MO is antibonding sigma orbital, and because it has not occupied, it does not affect the bonding sigma orbital caused by in phase overlap between 2pz AOs.
Furthermore, this MO is energetically very low in the LUMO region( E= 0.19634 a.u.).