Rep:Mod:217GASE
NH3 Molecule
RB3LYP was the method used for this molecule
6-31G(d.p) was the basis set used
The final energy in au was -56.55776873
The RMS gradient was 0.00000485
Point group of the molecule = C3v
The N-H bond distance is 1.01798 angstroms
The H-N-H bong angle is 105.741 degrees
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986272D-10
test molecule |
The optimisation file is linked to here
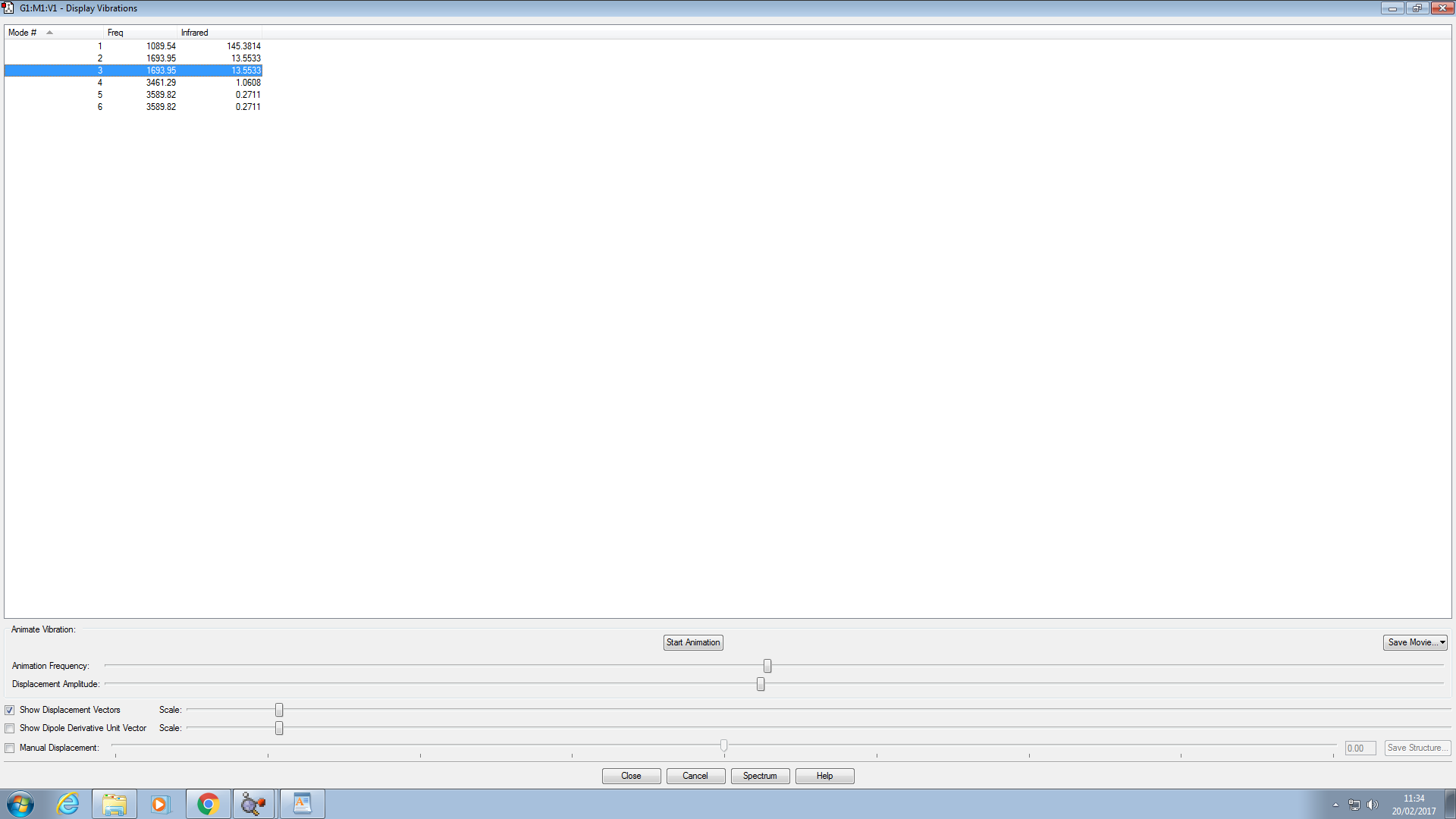
6 modes are expected from the 3N-6 rule.
Modes 2 and 3,as well as 5 and 6 have degenerate energies.
Modes 1,2 and 3 are bending. Modes 4,5 and 6 are stretching.
Modes 1,3 and 4 are symmetric.
Mode 1 is the umbrella one.
4 bands would be degenerate.
The charge on the Nitrogen atom is -1.125 and the charge on each hydrogen atom was 0.375.
I would have expected the Nitrogen charge to be -3 and each hydrogen having +1 charge.
The Hydrogen Molecule
RB3LYP was the method used for this molecule
6-31G(d.p) was the basis set used
The final energy in au was -1.17853936
The RMS gradient was 0.00000017
Point group of the molecule = D*H
The H-H bond distance is 0.74279 angstroms
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.164080D-13
The only frequency is 4465.68, so there are no negative frequencies.
The Nitrogen Molecule
RB3LYP was the method used for this molecule
6-31G(d.p) was the basis set used
The final energy in au was -109.52412868
The RMS gradient was 0.00000060
Point group of the molecule = D*H
The N-N bond distance is 1.10550 angstroms
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-3.400879D-13
The only frequency is 2457.33, so there are no negative frequencies.
Energy Changes
The equation of ammonia formation is as follows:
3H2 + N2 → 2NH3
E(NH3)= -56.55776873 2*E(NH3)= -113.1155375 E(N2)= -109.52412868 E(H2)= -1.17853936 3*E(H2)= -3.53561808
From these energy values, we can then use the stoichiometry of the equation to find the enthalpy of formation of ammonia as follows:
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074
Energy change in kJ/mol = -146.49
The ammonia product is more stable than its gaseous reactants because the energy change calculated is negative, an exothermic reaction. The ammonia has a lower energy. The calculated value is however much higher than experimentally calculated as shown in the following https://en.wikipedia.org/wiki/Standard_enthalpy_of_formation. This is because the conditions used in the Haber process make it possible to reduce the energy used in the formation of ammonia.
SiH4 Molecule
RB3LYP was the method used for this molecule
6-31G(d.p) was the basis set used
The final energy in au was -291.88802760
The RMS gradient was 0.00000002
Point group of the molecule = TD
The Si-H bond distance is 1.48485 angstroms
The H-Si-H bong angle is 109.471 degrees, so the molecule has a terahedral shape.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-2.452659D-14
test molecule |
The optimisation file is linked to [| here]
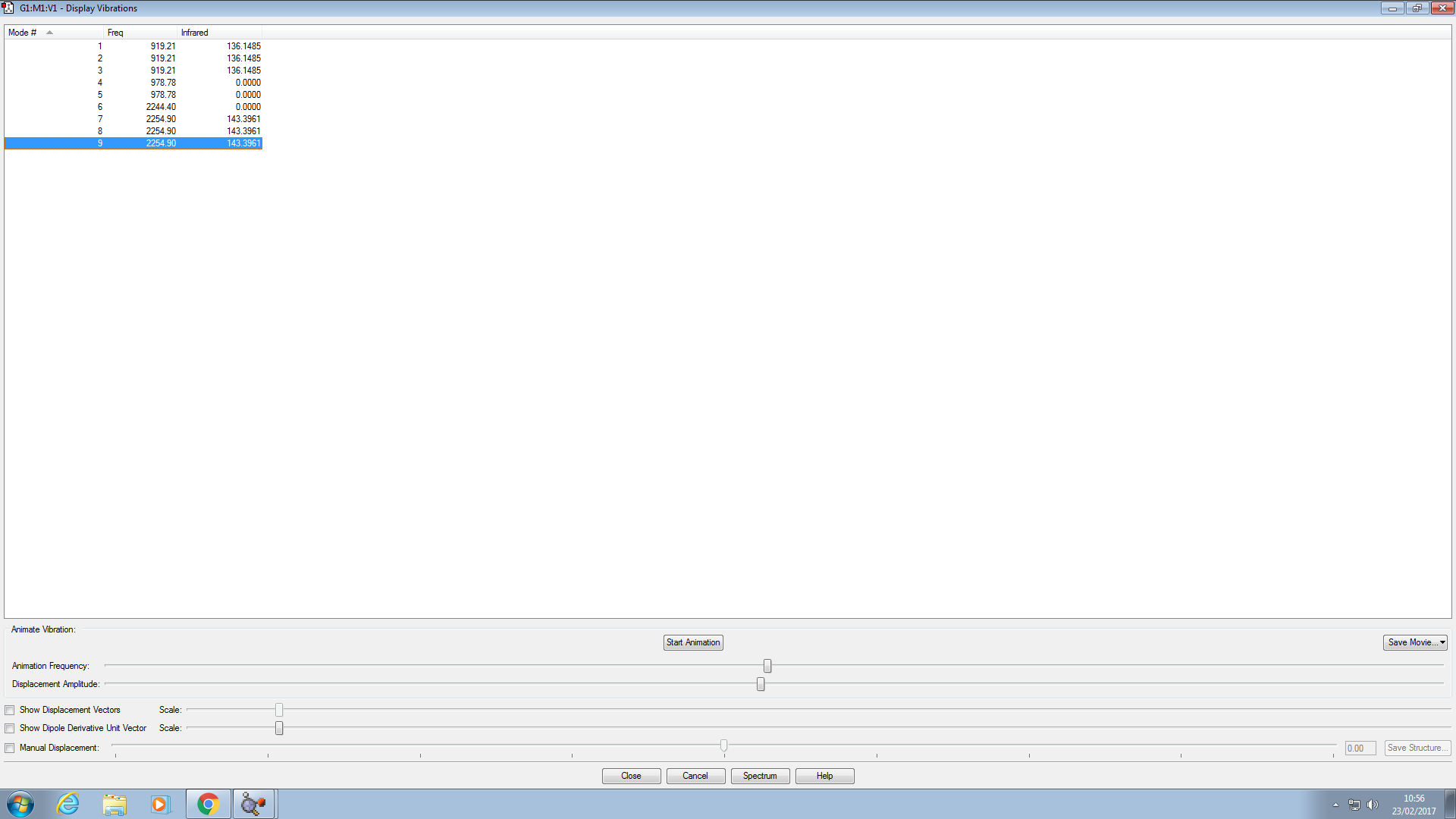
There are 9 vibrational modes observed.
The modes 1,2,3 are degenerate. As well as 4,5 and 7,8,9, with 3 different values.
2 bands would be seen because there are only 2 infrared active modes (figures).
Modes 1 to 5 are all bending, and modes 6 to 9 are stretching.
Modes 4,5 and 6 are symmetric.
The Si atom has a charge of 0.629, while each hydrogen atom has a charge of -0.157. This is different from the expected values which were Si:-4 and H:+1.
Energy Changes
The equation of SiH4 formation is as follows:
Si + 2H2 → SiH4
E(H2)= -1.17853936 2*E(H2)= -2.35707872 E(Si)= 0 E(SiH4)= -291.88802760
Note that the energy of Si is 0 because it is a unimolecular atom with no bonds.
From these energy values, we can then use the stoichiometry of the equation to find the enthalpy of formation of SiH4 as follows:
ΔE=E(SiH4)-[E(Si)+2*E(H2)]= -289.5309519
Energy change in kJ/mol = -760163.51
This show that SiH4 is more stable than its reactants as the reaction is exothermic.
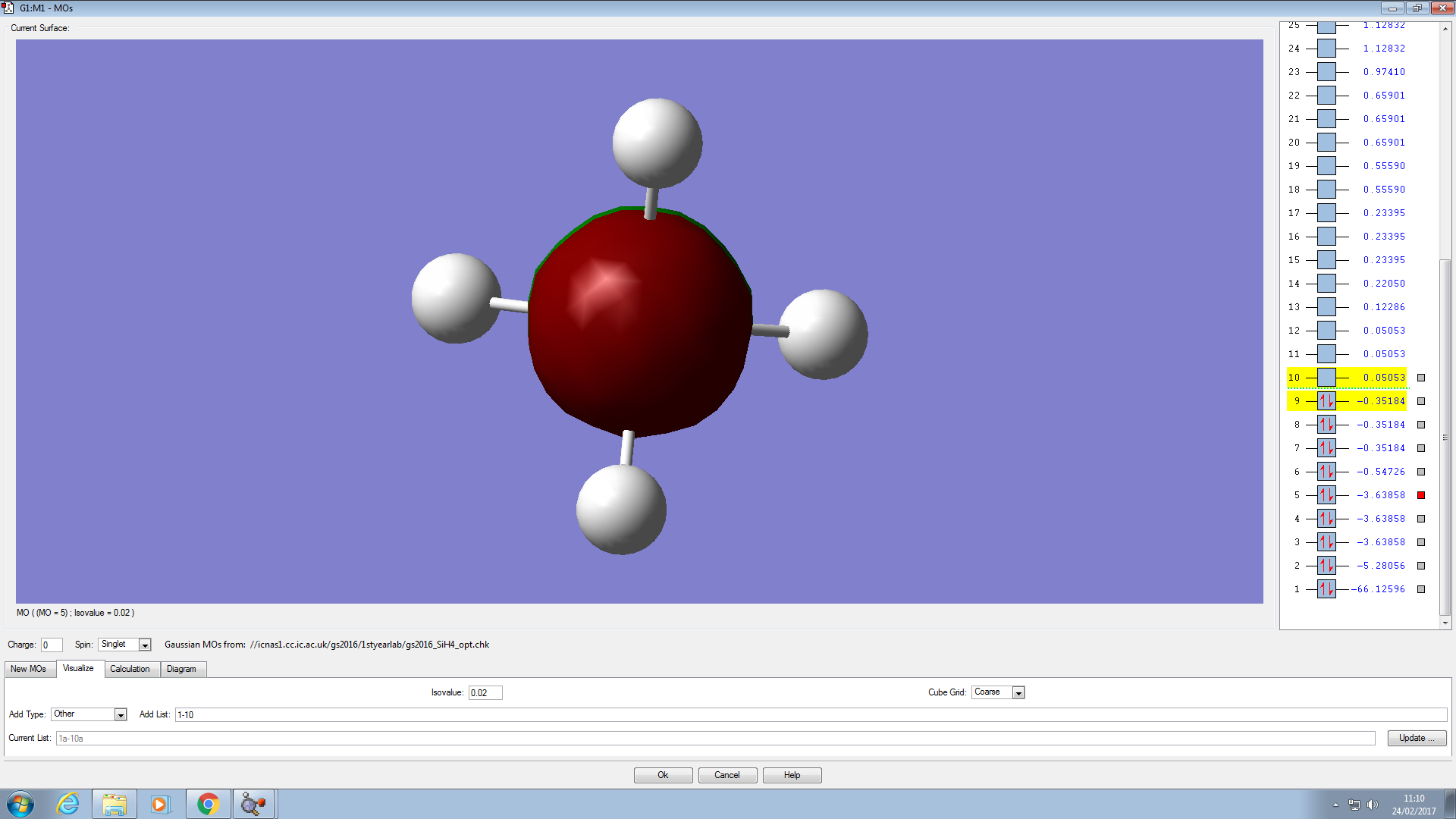
Molecular Orbitals
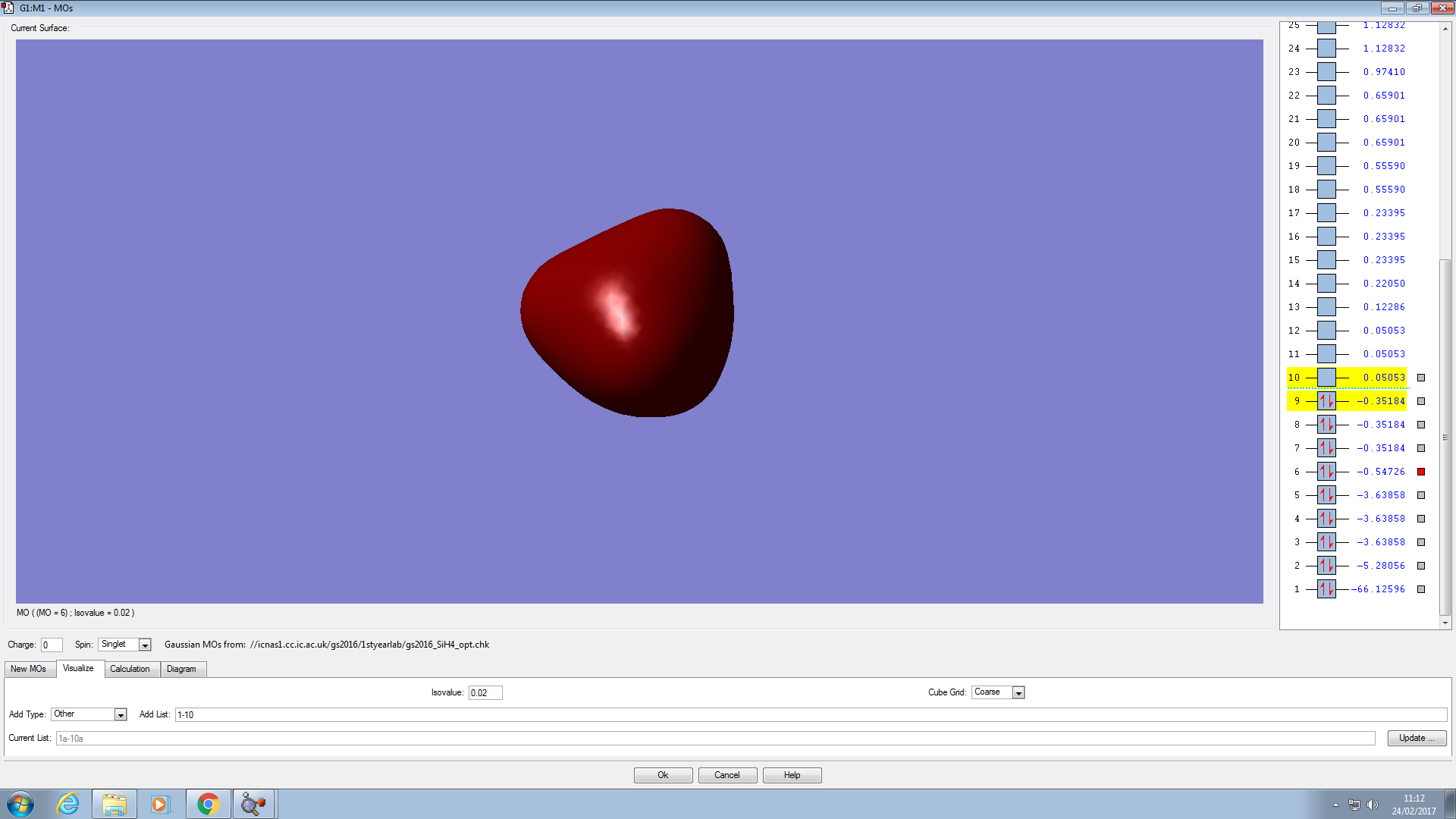
This is a 3s molecular orbital. It does not contribute to the bonding because its energy is lower than that of the 3p, i.e, there is no degeneracy so the orbital is not hybridised.
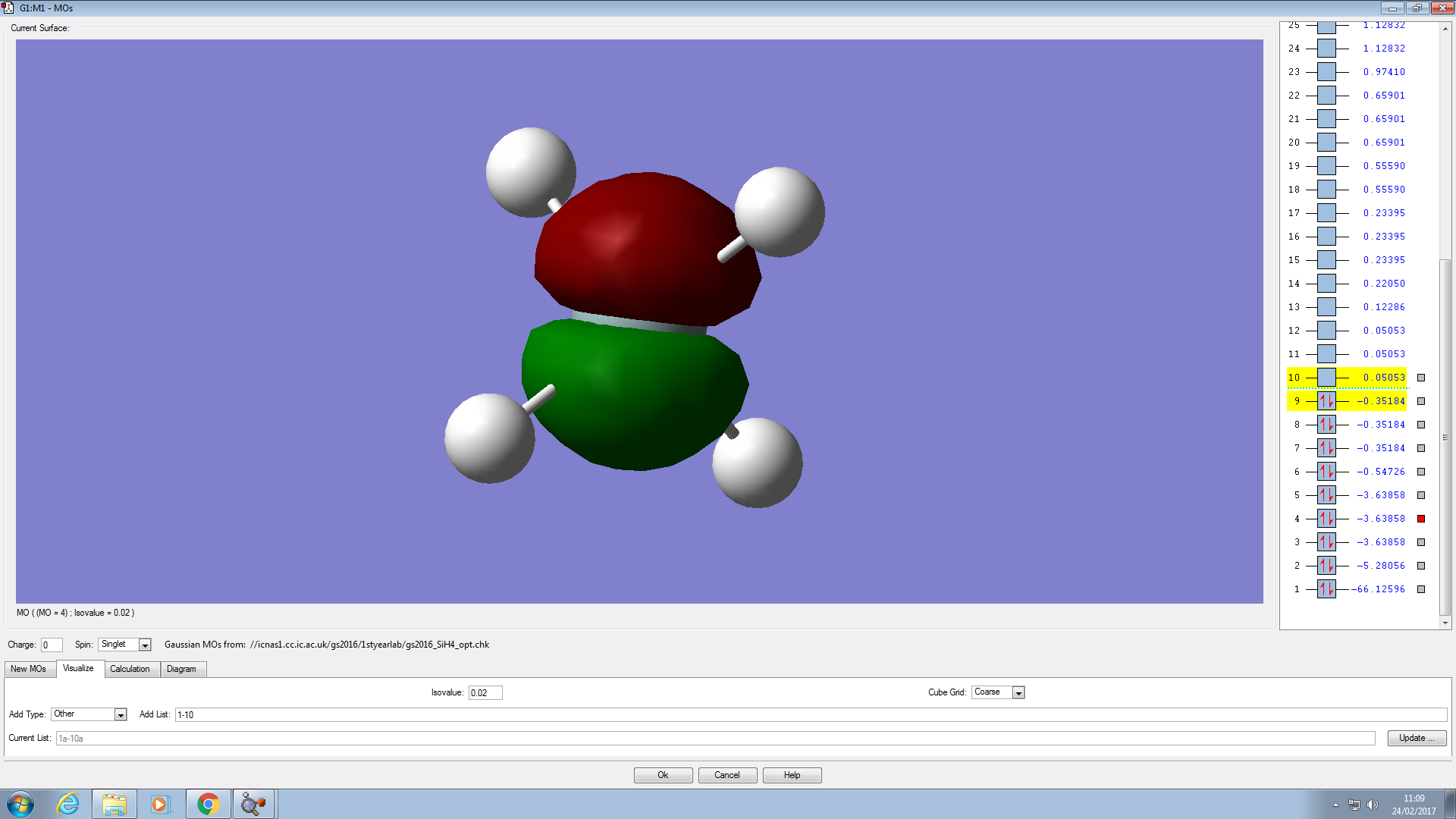
These are all degenerate 2p orbitals. They have the same energies and are facing different directions (2px, 2py and 2pz). The 3p orbitals have the same shapes and directions but are much larger. The 2p orbitals have no effects on the MOs. The 3p orbitals however bond with the hydrogen electrons and are the LUMO.
This is the orbital with the deepest energy. It is a filled 1s orbital and has no effect on bonding. It is not visible because it is very small and within the Si atom.