Rep:Mod:201000CBF

NH₃ Optimisation

• Calculation Method : RB3LYP
• Basis Set : 6-31G(d.p)
• Final Energy : -56.55776873 a.u.
• Point Group : C3v
• RMS Gradient : 0.00000485 a.u.
• N-H bond distance : 1.01798 ± 0.001 Å
• H-N-H bond angle : 105.741 ± 1°

The optimisation file is linked to here

Item Section

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.986280D-10

Jmol of structure:

optimised molecule

Table of vibrations and IR intensity

wavenumber cm-1	1090	1694	1694	3461	3590	3590
symmetry	A1	E	E	A1	E	E
intensity arbitrary units	145	14	14	1	0	0
images

Snapshot of the Display Vibrations table

Questions:

• How many modes do you expect from the 3N-6 rule? - 6
• Which modes are degenerate? - The two modes with frequency at 1694 cm^-1 and the two with frequency at 3590 cm^-1
• Which modes are "bending" vibrations and which are "bond stretch" vibrations?
  • 1090 cm^-1 : bending
  • Two degenerate at 1694 cm^-1 : bending
  • 3461 cm^-1 : bond stretch
  • Two degenerate at 3590 cm^-1 : bond stretch
• Which mode is highly symmetric? - the mode at 3461 cm^-1
• Which mode is known as the "umbrella" mode? - the mode at 1090 cm^-1
• How many bands would you expect to see in an experimental spectrum of gaseous ammonia? - two bands; one at 1090 cm^-1 and one at 1694 cm^-1. The other modes of vibration are highly symmetrical and produce a very small change in dipole moment, giving very small intensities which can't be seen in the IR spectrum.

Charge distribution in NH₃

As Nitrogen is more electronegative than Hydrogen we would expect Nitrogen to have a partial negative charge and Hydrogen a partial positive charge. This is in accordance with the numbers predicted by Gaussian;

• Charge on N: -1.078
• Charge on H: 0.359

N₂ Optimisation

• Calculation Method : RB3LYP
• Basis Set : 6-31G(d.p)
• Final Energy : -109.52412868 a.u.
• Point Group : D_∞
• RMS Gradient : 0.02473091 a.u.
• N-N bond distance : 1.10550 ± 0.001 Å

The optimisation file is linked to here

Item Section

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 Predicted change in Energy=-3.400988D-13

Jmol of structure:

optimised molecule

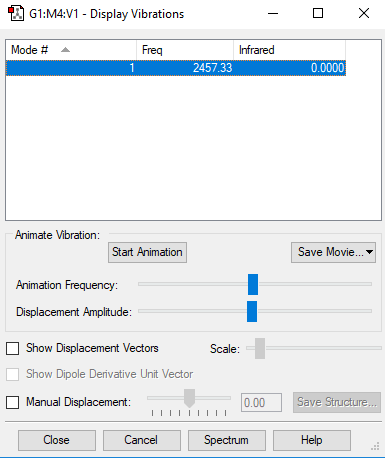
Table of vibrations and IR intensity

wavenumber cm-1	2457
symmetry	SGG
intensity arbitrary units	0

Snapshot of the Display Vibrations table

Questions:

• How many modes do you expect from the 3N-5 rule? - 1 stretching mode is present

Charge distribution in N₂

As N₂ is homonuclear there is no dipole moment and no charge on the individual N atoms.

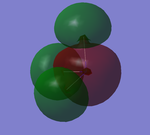
N₂ MOs: HOMO and LUMO

• HOMO energy = -0.42688
• LUMO energy = -0.02412

H₂ Optimisation

• Calculation Method : RB3LYP
• Basis Set : 6-31G(d.p)
• Final Energy : -1.17853936 a.u.
• Point Group : D_∞
• RMS Gradient : 0.00000017 a.u.
• H-H bond distance : 0.74279 ± 0.001 Å

The optimisation file is linked to here

Item Section

          Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-1.164079D-13

Jmol of structure:

optimised molecule

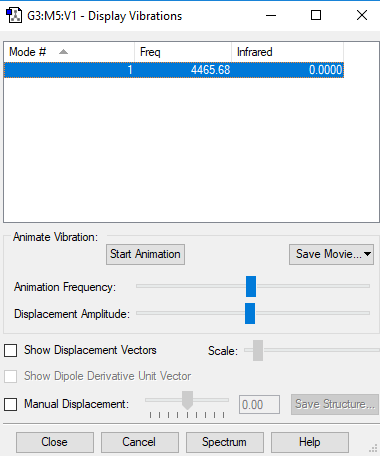
Table of vibrations and IR intensity

wavenumber cm-1	4466
symmetry	SGG
intensity arbitrary units	0

Snapshot of the Display Vibrations table

Questions:

• How many modes do you expect from the 3N-5 rule? - 1 stretching mode is present

Charge distribution in H₂

As H₂ is homonuclear there is no dipole moment and no charge on the individual H atoms.

N₂ in a mono-metallic TM complex

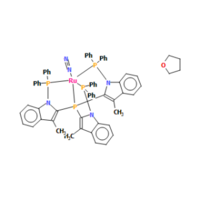
• Unique Identifier: DEKFUX
• N-N bond length in complex: 1.0866 Å
• N-N bond length from Gaussian: 1.10550 ± 0.001 Å

The structure can be found here: [[1]]

The bond length is calculated from the amount of electron density around the atoms. If we have a large electron density region between two positive nuclei, they will be attracted to it shortening the bond.

In our complex, Nitrogen is bound to a Ru atom, this acts as an electron withdrawing group reducing the electron density between the two atoms. This means there is greater repulsion between the two and the bond length is slightly lengthened.

The Haber-Bosch process

E(NH₃)= -56.5577687 a.u.

2*E(NH₂)= -113.115538 a.u.

E(N₂)= -109.5235911 a.u.

E(H₂)= -1.1785394 a.u.

3*E(H₂)= -3.5356181 a.u.

ΔE= 2*E(NH₃) - [E(N₂) + 3*E(H₂)] = -0.0563288 a.u.

ΔE = -147.8912644 kJ/mol

Ammonia is more stable because the reaction is exothermic therefore its energy is lower than the reactants'.

NF₃

• Calculation Method : RB3LYP
• Basis Set : 6-31G(d.p)
• Final Energy : -354.07131058 a.u.
• Point Group : C3v
• RMS Gradient : 0.00010256 a.u.
• N-F bond distance : 1.38404 ± 0.001 Å
• F-N-F bond angle : 101.830 ± 1°

The optimisation file is linked to here

Item Section

        Item               Value     Threshold  Converged?
 Maximum Force            0.000164     0.000450     YES
 RMS     Force            0.000108     0.000300     YES
 Maximum Displacement     0.000612     0.001800     YES
 RMS     Displacement     0.000296     0.001200     YES
 Predicted change in Energy=-1.274066D-07

Jmol of structure:

optimised molecule

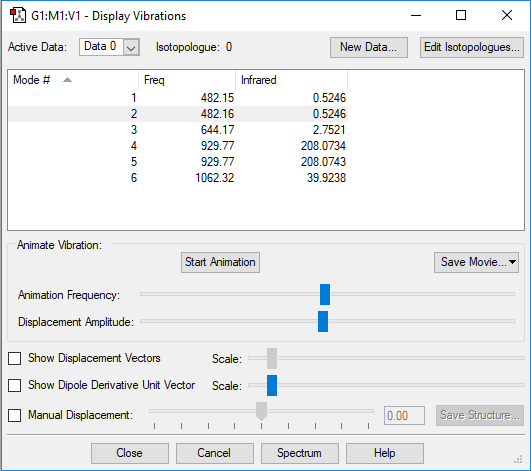
Table of vibrations and IR intensity

wavenumber cm-1	482	482	644	930	930	1062
symmetry	E	E	A1	E	E	A1
intensity arbitrary units	1	1	3	208	208	40
images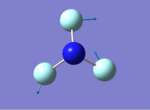

Snapshot of the Display Vibrations table

Questions:

• How many modes do you expect from the 3N-6 rule? - 6
• Which modes are degenerate? - The two modes with frequency at 482 cm^-1 and the two with frequency at 930 cm^-1
• Which modes are "bending" vibrations and which are "bond stretch" vibrations?
  • Two degenerate at 482 cm^-1 : bending
  • 644 cm^-1 : bending
  • Two degenerate at 930 cm^-1 : bending
  • 1062 cm^-1 : bond stretching
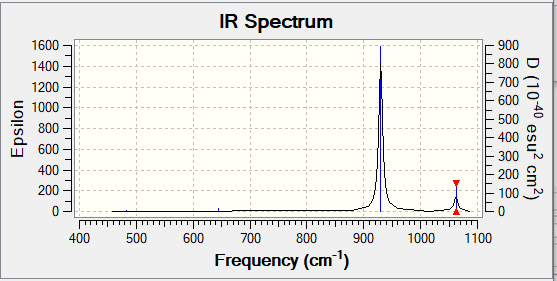
• How many bands would you expect to see in an experimental spectrum of NF₃? - two bands; one at 930 cm^-1 and one at 1062 cm^-1. The other modes of vibration produce a very small change in dipole moment, giving very small intensities which can't be seen in the IR spectrum.

This is the IR spectrum predicted by Gaussian, which clearly shows 2 bands.

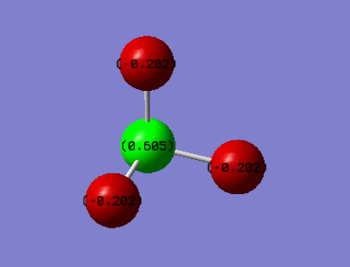
Charge distribution in NH₃

As Fluorine is more electronegative than Nitrogen so, we would expect Fluorine to have a partial negative charge and Nitrogen a partial positive charge. This is in accordance with the numbers predicted by Gaussian;

• Charge on N: 0.605
• Charge on F: -0.202

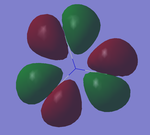
MO orbitals in NF₃

• HOMO ENERGY: -0.35162 a.u.
• LUMO ENERGY: 0.01947 a.u.

Orbitals
MO	3	5	8	11	16
Energy a.u.	-24.76570	-1.35870	-0.81874	-0.57102	-0.42224
Occupied?	YES	YES	YES	YES	YES
Descriptions	This image shows the s AOs for each of the Fluorines around the central N atom. They are buried deep in energy and therefore don't interact with the orbitals in Nitrogen remaining as AOs.	Here we can see the combination of 3 2s orbitals from Fluorine with the s orbital in the central Nitrogen atom to form an MO. The energy is much greater than for the AOs, but still lower than the HOMO/LUMO region.	The p orbitals in each of the Fluorines are interacting with the central s-orbital from the Nitrogen to form a clear central antibonding region and bonding lobes around the peripheral Fluorines.	The combination of the vertical p-orbitals of all of our atoms result in two clear regions of bonding and antibonding character. The bonding region is smaller due to the orientation of the p-orbitals, which are slightly tilted towards each other.	This shows a non-bonding orbital made up of the three horizontal p orbitals of the fluorines. It is very close to the HOMO/LUMO region. The p orbitals can't overlap because they don't have the correct symmetry, they are therefore high in energy as they can't interact and stabilise. Marking Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard. Wiki structure and presentation 1/1 Is your wiki page clear and easy to follow, with consistent formatting? YES - good structure well done. Do you effectively use tables, figures and subheadings to communicate your work? YES NH3 1/1 Have you completed the calculation and given a link to the file? YES Have you included summary and item tables in your wiki? YES Have you included a 3d jmol file or an image of the finished structure? YES Have you included the bond lengths and angles asked for? YES Have you included the “display vibrations” table? YES Have you added a table to your wiki listing the wavenumber and intensity of each vibration? YES Did you do the optional extra of adding images of the vibrations? YES Have you included answers to the questions about vibrations and charges in the lab script? YES - excellent explanations. N2 and H2 0.5/0.5 Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges) YES Crystal structure comparison 0/0.5 Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule? YES Have you compared your optimised bond distance to the crystal structure bond distance? YES - however you stated that the bond is lengthened in the complex, this is incorrect, your data is that the n-n bond is shorter in the complex. Haber-Bosch reaction energy calculation 0.5/1 Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)] YES Have you reported your answers to the correct number of decimal places? NO - you should have rounded to 1 d.p. (in kJ/mol) at the most. Do your energies have the correct +/- sign? YES Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product? YES Your choice of small molecule 3/5 Have you completed the calculation and included all relevant information? YES Have you added information about MOs and charges on atoms? YES - overall you have done well explaining the charges and vibrations. You have also explained the contributions of the AOs to the MOs correctly. However you are confused about the bonding/antibonding nature of MOs. The green and red colours signify positive and negative phases of the MOs, red is not antibonding and green is not bonding. Talk to one of your tutors and show them your wiki if you don't understand what I mean here. Independence 0.5/1 If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far You looked at the N2 MOs, you didn't get a whole extra mark for this as you made no comment on them.