Rep:Mod:200529ypphysical
The Cope Rearrangement
This computational lab makes use of a few of the methods used be GaussView to determine the transition state of the 3,3-sigmatropic shift shown below.

The concerted, pericyclic reaction can occur via a boat- or chair-like transition state. In order to help identify the transition state of this reaction, 1,5-hexadiene was constructed first with the middle 4 atoms in an anti conformation then in a gauche conformation. A simpler, and thus less computationally expensive level of theory was used (HF,3-21G) to minimise both the anti and gauche conformers. The results are displayed in the table below.
| Antiperiplanar | Gauche | |
|---|---|---|
| Conformation | 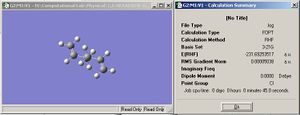 |
 |
| Energy/kCalmol-1 | -145389.29192814 | -145389.37101945 |
We would expect the anti- conformer to be more thermodynamically stable than the gauche- conformer. Although there is a stabilising gauche effect (an interaction between σ*C-X and σC-H on an adjecent carbon) this is only significant for a very electron withdrawing X group, for this dialkene the overwhelming conformational control is the preference of the relativly bulky CH=CH2 groups to be antiperiplanar. This is confirmed by the 0.0791kCal.mol-1 stabilisation energy of anti- over gauche.
The symmetry of the minimised antiperiplanar molecule is shown to be Ci. The more symmetric gauche conformer should be C2, however in the minimisation of the molecule, GaussView modified the dihedral angles of the central four carbon atoms very slightly off the 00 necessary for this structure to be considered C2 symmetry.
We were then asked to construct the anti2 structure of 1,5-hexadiene and compute it's energy at different levels of theory.
anti2 Conformer of 1,5-cyclohexadiene
Since the structre has already been minimised via a HF/3-21G method in the step above we can instantly compare the energy obtained with that stated in the labscript in order to ensure the correct structure has been optimised.
The energy of the optimised structre (-231.69253517 hartree) and the symmetry (Ci) fit perfectly with those cited in the lab script1 (-231.69254 hartree and Ci). Following this confirmation of structure, a B3LYP/6-31* calculation method was employed and an optimised energy of -234.61171549 hartree was read. We would expect this more intensive calculation to give a slightly lower value forenergy than the HF level of calculation, this is due to the added terms in the b3lyp minimising the overall energy of the molecule. After this more intensive minimisation was carried out a frequency analysis calculation at the same level of theory was carried out. Key energies are listed in the table below.
| Energy | Value/hartree |
|---|---|
| Eelec + ZPE | -234.469176 |
| E = E + Evib + Erot + Etrans | -234.461834 |
| Term including correction for RT | -234.460890 |
| Term including contribution of the Free Energy | -234.500744 |
References & Literature
Optimising the Chair and Boat Transition States
Chair Transition State

An allyl fragment was constructed in ChemBio3D and inported as a .gjf file into GaussView. This allowed a HF/3-21G method of calculation to be carried out. The structure obtained from this minimisation (shown to the right) was then used to produce a "guess" structure for the chair transition state. An optimisation and frequency calculation was selected from the Calculations menu of the Gaussian tab. In the key words section, Opt=NoEigen was input, telling the programme not to crash if more than one imaginary vibration is returned, and a HF/3-21G calculation was run.

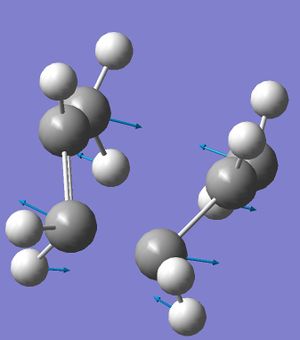
After the job had run, the list of vibrations was analysed and as the lab script suggested there was an imaginary vibration at ~818cm-1. This vibration did indeed correspond to the cope rearrangement and is shown to the right. You will notice that the atoms between which the C-C bond is breaking (1) are moving apart from one another and the carbon atoms between which the new C-C bond is being concertedly formed (3) are moving towards one another in this [3,3] sigmatropic reaction.
Boat Transition State

The optimisation of the "boat" transition structure was carried out using a QST2 method of calculation. This method interpolates two structures and finds a midpoint which is assumed to be the transition structure. As such both the starting reactant 1,5-hexadiene and the final product (also a 1,5-hexadiene) must be input, with correct numbering, into the GaussView program. Since this is a [3,3]-sigmatropic reaction, the numbers of the atoms input into GaussView are shown to the right.

The top image a) corresponds to the first qst2 calculation run for the [3,3]-sigmatropic reaction. This calculation returned an incorrect structure shown directly to the right. a qst2 method requires structures that are very close to the transition structure, otherwise a "false" transition structure could be found, this is the example shown to the right. To overcome this, the structures of the input molecules were modified to be close to the boat transition structure. This was done through the use of the modify dihedral angle tool on GaussView. Image b) shows this new, modified structure and a "boat-like" intermediate between the left and right image can be easily imagined. After running a second qst2 calculation on these modified structures a "boat-like" transition state was obtained and is shown below the incorrect transition structure. Again, looking at the imaginary vibration (at -839.967cm-1) it can be seen that this vibration corresponds to a [3,3]-sigmatropic shift reaction. We can imagine the bond between the carbons moving away from each other breaking while another bond forms between the carbons in the 3 position. An IRC was carried out to determine which conformer of 1,5-hexadiene was responsible for the chair transition state.
IRC Calculation For Chair transition State
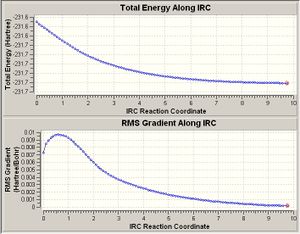
The HF/3-21G optimised structure of the chair transition state was opened up and IRC was selected from the Gaussian menu. To the right is shown the graph of the energies of each of the 100 geometries calculated by the IRC method. As can be seen, a minimum energy was not reached (the RMS gradient does not become positive towards the right of the x-axis). As such, the lowest point (point 100, highlighted by a red circle) was copied and a normal HF/3-21G method was carried out to minimse this structure. The optimised structure is shown below.
The symmetry of this optimised 1,5-hexadiene structure is C1 and as such this structure must be either the gauche3, gauche5, gauche6 or the anti4 structure. A comparison of the energy with the energies of the different structures shown on the lab script1 will indicate which of these structures has been optimised. The value of -231.69167 hartree for the optimised structure is closest to the value of -231.69267 for the gauche3 structure and this along with a comparison of the structural shape of each confirms that the chair transition state was formed by the [3,3]-sigmatopic shift of the gauche3 conformers.
References And Literature
The Diels-Alder Reaction
The first reaction to be studied is that between butadiene and ethene. In order to determine whether this is an allowed reaction we can compare the symmetry of the HOMO of butadiene with the symmetry of the LUMO of ethene. In order for the diels alder reaction to occur, there must be significant overlap between these two interacting orbitals. A satisfactory overlap only occurs if the two orbitals (HOMObutadiene-LUMOethene) have the same symmetry (i.e. are both antisymmetric or both symmetric)
Butadiene was first constructed in ChemBioUltra 3D and imported as a .gjf file into GaussView. An AM1 Semiempirical method was then used to construct the MO diagram of butadiene, this is shown to the right. A mirror plane through the molecule effectively "inverts" the phase of the orbital lobes and this orbital can therefore be said to be antisymmetric with respect to the plane. The below table shows both the HOMO and LUMO of butadiene and the symmetries of the orbitals with respect to the primary rotational axis and the plane of the molecule.
| MO | Symmetry with Respect to the Axis | Symmetry with Respect to the Plane |
|---|---|---|
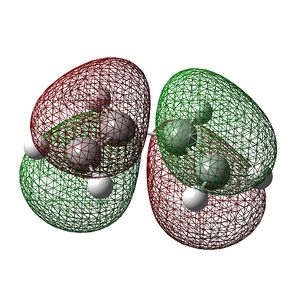 |
Symmetric | Antisymmetric |
 |
Antisymmetric | Antisymmetric |
Compare these symmetries with the symmetries of the HOMO and LUMO in the transition structure.
| MO | Symmetry with Respect to the Axis | Symmetry with Respect to the Plane |
|---|---|---|
 |
Antisymmetric | Antisymmetric |
 |
Antisymmetric | Symmetric |

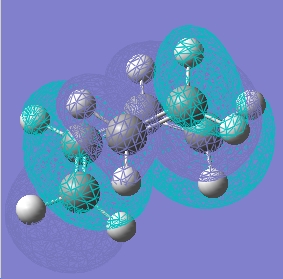
We can determine which molecular orbitals were involved in the formation of this final product by analysing the symmetry of the butadiene fragment in the HOMO of the transition state and comparing this symmetry with that of the HOMO and LUMO of butadiene. IN the transition state, the butadiene fragment is symmetric with respect to the rotation axis, but is anti symmetric with respect to the plane symmetry. This is the same symmetry as the HOMO of butadiene and we can therefore say that this Diels Alder product is formed through interaction of the HOMObutadiene and the LUMOethene. Looking at the symmetry of the ethene fragment in the HOMO of the transtion structure, we see that it is antisymmetric with respect to the plane of symmetry, but symmetric with respect to the axis of symmetry. This corresponds with the symmetry of the LUMO of ethene, shown to the right and we can therefore confirm that this diels alder product was formed through the following interaction : HOMObutadiene-LUMOethene.

The image to the right shows the imaginary vibration (at -430.395cm-1) which corresponds to the Diels Alder reaction. The atoms highlighted with a red spot are seen to move towards and away from each other with equal vectors and we can therefore state that both bonds are formed in a synchronous manner, which is what we would expect from a pericyclclic (concerted) reaction.
In order to determine the nature of the partially formed C-C σ bond, the table below shows the bond lengths of each C-C π and σ bond, along with that of the partially formed bond.
| Bond | Bond Length /Å |
|---|---|
 |
1.37867 |
 |
1.37657 |
 |
1.41288 |
 |
2.29289 |
The partially formed bond is not surprisingly longer than the π bond and is closer in lengh to the C-C σ bond.
Cyclohexadiene + Maleic Anhydride
A qst3 method was used to calculate the optimised structures of the endo- and exo- transition states of the reaction between cyclohexadiene and maleic anhydride. The table below shows an example of the screen pre-submission of the qst3, the optimised transition structure and the energy of that transition state.
| Product | Reaction "Pathway" | Transition State | Energy/hartree |
|---|---|---|---|
| Exo- |  |
 |
-605.57563766 |
| endo | 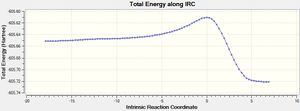 |
 |
-605.47846909 |
The imaginary vibrations in both the exo and endo transition states both show the concerted, synchronous formation of C-C bonds.
Not surprisingly, both these energies are higher than the starting and end products of this reaction, since this is a transition state it is therefore an energy maximum. What is interesting however is that although the exo product will be more thermodynamically stable, due to a decrease in steric strain, the endo actually has a lower activation barrier (lower energy transition state). This difference is -255.161kJmol-1 and is therefore not very significant when compared to RT (~2.5kjmol-1).
