Rep:Mod:200529ypinorganic

Computational Inorganic Chemistry

BH₃ Introduction

Optimisation of BH₃

After carrying out a FOPT type calculation via a RB3LYP method, using a 3-21G basis set, optimisation of BH₃ was achieved. The H-B-H bond angle and B-H bond length were measured. The optimised energy was found to be -26.46226438 a.u. There is a dipole moment, as expected, of 0D and the point group is given as being D₃H. The job took 29.0s.

B-H Bond Length	H-B-H Bond Angle
2.35099Å	120.0000

IR Vibrations of BH₃

no.	Form Of Vibration	Frequency	Intensity	Symmetry D3H Point Group
1		1145.71	92.6991	A2"
2		1204.66	12.3789	E'
3		1204.66	12.3814	E'
4		2592.79	0	A1'
5		2731.31	103.837	E'
6		2731.31	103.83	E'

The table above shows the 6 possible vibations of BH₃ when subjected to IR radiation. The table shows a snapshot of each vibration, it's intensity on an IR spectra, the frequency at which this vibration will occur and the symmetry label of the vibration within the D_3h point group.

Notice how one of the vibrations (number 4) has an intensity of 0. Although there is vibration, it is totally symmetiric, having a point group of A₂" meaning there is no overall change in dipole moment of the molecule and therefore no absorption is seen.

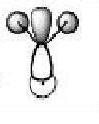
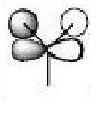
MO Diagrams (Qualitative and Quantitative) of BH₃

Orbital	Generated (Quantitative) MO	Qualitative MO 1
LUMO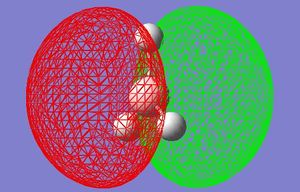
HOMO
HOMO-1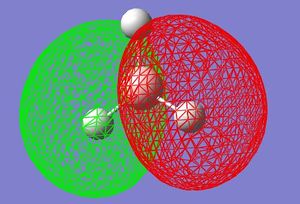
HOMO-2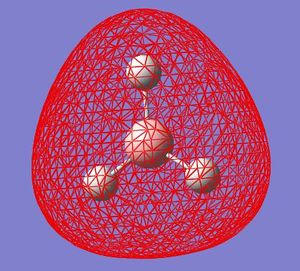
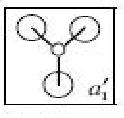HOMO-3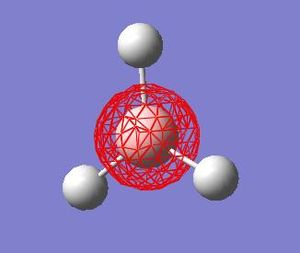

These quantitative MO results show a close symmetrical relationship with the qualitative MOs of BH₃. A qualitative approach to constructing MO diagrams requires little or no computing time and provides a pretty good description of bonding in simple, small molecules.

References and Literature

1. All qualitative MO drawings are taken from Dr P. hunt's Teahcing Page , http://www.ch.ic.ac.uk/hunt/teaching/teaching_MOs_year2/L3_Tut_MO_diagram_BH3.pdf

BCl₃

After carrying out a DFT optimisation calculation using the B3LYP method and a 3-21G basis set the following results were obtained for a molecule of PCl₃

B-Cl Bond Length	Cl-B-Cl Bond Angle
Å	1200

NH₃ (Small Molecule Project)

The same method as above was employed to minimise the energy and structure of ammonia. The results are below.

Measurement	Value
Visualisation
Point Group	C3v
N-H Bond Distance	1.02216Å
H-N-N Bond Angle	110.2420
Energy	-56.229 a.u.
Dipole Moment	1.8678D

The overall dipole moment of 1.8678D is due to the nitrogen lone pair being sp₃ hybridised, forcing the N-H covalent bonds out of plane, making the molecule non planar.

NH₃ IR Vibrations

no.	Form Of Vibration	Frequency	Intensity	Symmetry C3v Point Group
1		779.857	251.215	A1
2		1746.89	13.5909	E
3		1746.89	13.5915	E
4		3384.54	1.2245	A1
5		3536.02	1.4224	E
6		3536.02	1.4221	E

MO Diagrams For Ocupied Energy Levels and the LUMO for NH₃

Generated (Quantitative) MO	Qualitative MO
LUMO
HOMO
HOMO-1
HOMO-2
HOMO-3
HOMO-4

The Quantum Nature of Ammonia

Symmetry

Isomer Description	Optimisation Summary
Nitrogen tetra valent (all bonds equivalent)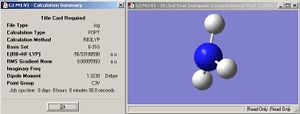
One bond constructed longer than other bonds (1.01Å c.f. 1.00Å)
High symmetry NH3

When one N-H bond is increased in length by just 0.1Å, it is enough to transform the symmetrical C_3v to a very unsymmetrical C₁ point group, owing to the loss of the C₃ symmetry element.

Although the bond (for the C₁ isomer) was changed by 0.01Å, the resulting optimised structure is very much closer to C_3vsymmetry, the bond length differing by only 10^-5Å. The modified, lengthened bond is infact shorter than the other 2 in the optimised structure (1.00594Å c.f. 1.00595Å). The observation of the very slight difference in bond lengths in the optimised structure of C₁ ammonia suggests that the symmetry of a molecule cannot be broken during optimisation; since the input molecule had C₁ symmetry, so the output optimisation must have C₁. The smallest possible difference (according to the program) in bond length is 10^-5Å, so the programme will set one bond to a length of this differene from the other 2 in order to ensure C₁ in the output.

The calculation times between the C_3v and C₁ optimisation can tell us how the programme uses symmetry to solve calculations. A decrease in symmetry (from C_3v to C₁) actually results in a longer calculation time (38.0s for C_3v c.f.44.0s for C₁) this suggests that Gaussview uses symmetry to shorten calculaions, perhaps by applying the same calculated values to all equivalent bonds. An optimisation calculation will be much quicker for a high symmetry molecule than for a lower symmetry molecule.

Not surprisingly, the lowest energy geometry of ammonia is the one that shows C_3v symmetry. Displayed below are the energies for the three optimised geometries of ammonia (in kJ/mol).

Point Group	Energy of molecule/ kJ/mol	ΔE (wrt Lowest Geometry/ kJ/mol
C3v	-148424.4664	0
C1	-148424.4709	4.5x10-3
D3h	-148148.1672	276.2992

Using More Extenisive Calculation Tools

Isomer Description	Optimisation Summary
Nitrogen tetra valent (all bonds equivalent)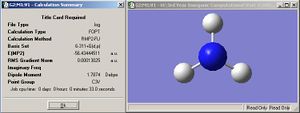
One bond constructed longer than other bonds (1.01Å c.f. 1.00Å)
High symmetry NH3

I ran these calculations a day after those in the previous section. The calculation times cannot be compared since different programs must ahve been running on my CPU on these two different days. The only explanation for the shorter calculation time, for the more complex basis set, is that these more complex calculations were run on a less cluttered CPU, increasing computional power. Again, the energies of each geometry are shown below.

Point Group	Energy of molecule/ kJ/mol	ΔE (wrt Lowest Geometry/ kJ/mol
C3v	-148168.6356	0
C1	-148168.6558	0.0202
D3h	-148148.1672	20.4684

The ΔE between the D_3h and the C_3v is much closer to the experimental value of 24.3kJ/mol. This lower energy barrier arrises since we used a more quantum mechanical approach in determining the optimised geometry of ammonia and allows us to say the "umbrella" effect can occur at room temperature.

A More Indepth Study of NH₃ Stretching Frequencies

A frequency analysis was carried out on a B3LYP/6-31G optimised ammonia molecule. Below are the tabulated intensities, frequencies and forms of vibration calculated.

Form of Vibration	Frequency of vibration	Intensity of Signal
A1	999.413	240.708
E	1673.65	28.676
E	1673.65	28.6756
A1	3484.88	2.6415
E	3627.94	3.9042
E	3627.94	3.904

For comparison, the IR vibrations obtained from carrying out an identical calculation on the D_3h transition state of ammonia are shown below.

Form of Vibration	Frequency of vibration	Intensity of Signal
A2"	-691.598	498.197
E"	1595.66	49.2729
E"	1595.66	49.2729
A2"	3525.11	0
E"	3738.78	52.9999
E"	3738.78	53.0016

Another table! This one shows how the same vibrational form can arise from different point group molecules (e.g. C_3v and D_3h)

C3v	D3h
A1	A2"
A1	A2"

The vibration responsible for the inversion mechanism is the first shown on this table. First of all, the hydrogens of C_3v ammonia will move parallel to the N-H bond, closer to nitrogen, where the D_3h A₂" vibration takes over, inverting the hydrogens.

Trans- and Cis- [Mo(CO)₄L₂ (L= P(CH₃)₃)

I would like to thank Ms. Florence Thomas¹ for providing the results to the molybdenum complex stretching calculations, since my files were all corrupted.

The two molecules pictured below were drawn in ChemDraw Ultra, imported as gjf files into Gaussian and minimised twice on the chemistry SCAN server:

1- First of all a lowleverl basis set was used and a B3LYP method with LANL2MB basis set optimised for basic geometry.

2- Secondly a better basis set was used, B3LYP method with LANL2DZ basis set. This optimised the molecule further, taking more computing time.

cis-Mo complex	trans-Mo complex

These optimised structures were then sent to SCAN once more for a frequency calculation. The output files were then checked and the form of vibrations were analysed. An interesting vibration is that shown below and is important since it results in a signal peak for the cis- complex but not for the molybdenum complex.

Isomer	Form of Vibration	Frequency	Intensity
Cis-		1857.42	417.318
Trans-		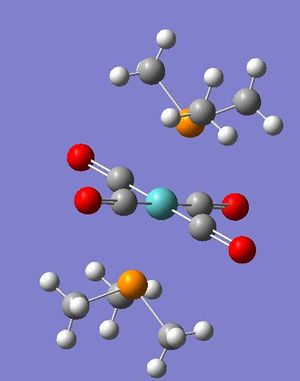1852.91	0

In the trans- complex, this vibration ~1850-1860cm^-1 is a highly symmetric transition and as such the overall dipole moment of the molecule does not change and a signal is not observed on the IR spectrum. Obviously this symmetric carbonyl stretching in the cis- complex will bring about a change in the overall dipole moment of the molecule, due to the two carbonyls perpendicular to one another, this change in dipole moment results in a signal on the IR spectrum. IR spectroscopy is therefore a powerful method for determining cis- trans- isomerism in complexes of the form [Mo(CO)₄L₂], for cis-complexes a peak will be seen at ~1855cm^-1 whereas no peak will be seen in this region for trans-.

References and Literature

1. https://www.ch.ic.ac.uk/wiki/index.php/Mod:crumblanium2802#Cis_and_Trans_Isomerism