Rep:Mod:1CSam11

                                                       ==Computational Lab Experiment 1C==

^[1]

Part 1

Thermodynamic Analysis of Cyclopentadiene Dimerisation and Hydrogenation Products

Molecule 1

molecule 1 minimised using MMFF94s force field

Type of Energy Contribution	Energy (kcal/mol)	Energy (kJ/mol)
Total Electrostatic Energy	13.01365
Total Van der Waal's Energy	3.54286
Total Out-of-Plane Bending Energy	30.77264
Total Torsional Energy	2.04136
Total Stretch Bending Energy	2.04136
Total Angle Bending Energy	0.01486
Total Bond Stretching Energy	12.80121
Total Energy	55.37344	231.838

Molecule 2

molecule 2 minimised using MMFF94s force field

Type of Energy Contribution	Energy (kcal/mol)	Energy (kJ/mol)
Total Electrostatic Energy	58.1907	243.633
Total Van der Waal's Energy	3.46742
Total Out-of-Plane Bending Energy	33.19047
Total Torsional Energy	-2.08217
Total Stretch Bending Energy	-2.94986
Total Angle Bending Energy	0.02197
Total Bond Stretching Energy	12.35798
Total Energy	14.18488

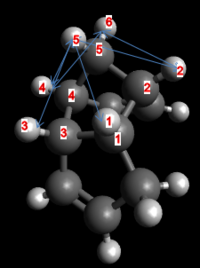
Molecules 1 and 2 have no partial charges. Of the reactant molecules, number 2, the endo Diels-Alder product, is the most unstable. The Van der Waal’s energy of the endo product is lower than number 1, the exo product, due to two favourable interactions available in the endo product, allowed by virtue of the reduced distance of the overhanging methylene bridging proton two protons of the cyclo-pentene ring. This is illustrated in the figure below:

Molecule 1 (Exo Product)

Van der Waal's Interaction	Interaction Length (Å)
H1-H5	2.632
H2-H5	3.448
H3-H5	2.667
H4-H5	2.668
H3-H6	2.622
H4-H6	2.624

Molecule 2 (Endo-product)

Van der Waal's Interaction	Interaction Length (Å)
H1-H5	2.541
H2-H5	2.667
H3-H5	2.574
H4-H5	2.667
H4-H6	2.624
H2-H6	2.623

Torsional and stretch bending energies of the endo product are also lower than for the exo product. Torsional strain is reduced in the endo product due to the gauche-antiperiplanar arrangement of alkyl substituents on bonds C1-C2 and C3-C4, which allows for increased σ-hyperconjugation and reduced steric clashing c.f the gauche-gauche conformation in the exo product. All other energy sources of the endo product are higher. Thus the dimerization is kinetically controlled, as molecule 2, the endo product is favoured over the lower total energy, more stable exo product. This agrees with literature computational modelling reports^[2] and experimental observations.^[3]

Molecule 3

molecule 3 minimised using MMFF94s force field

Type of Energy Contribution	Energy (kcal/mol)	Energy (kJ/mol)
Total Electrostatic Energy	50.72283	212.366
Total Van der Waal's Energy	3.3081
Total Out-of-Plane Bending Energy	30.85901
Total Torsional Energy	-1.92668
Total Stretch Bending Energy	0.06933
Total Angle Bending Energy	0.01531
Total Bond Stretching Energy	13.27678
Total Energy	5.12098

Important electrostatic interaction lengths between the nucleophilic allylic carbons and electrophilic overhanging hydrogens are noted below, alongside important H-H Van der Waal's interaction lengths. Numbering of interaction lengths is made with respect to the figure below.

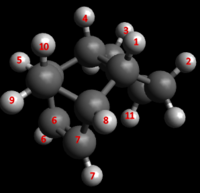
C-H Electrostatic Interaction	Interaction Lengths (Å)
C6-H9	2.589
C7-H9	2.589
H6-H11	2.803
H7-H11	2.803

H-H Van der Waal's Interaction	Interaction Lengths (Å)
H1-H2	2.29
H3-H4	2.29
H1-H8	2.502
H4-H5	2.502
H4-H10	2.666
H1-H10	2.542
H7-H9	3.423
H6-H9	3.423

Molecule 4

molecule 4 minimised using MMFF94s force field

Type of Energy Contribution	Energy (kcal/mol)	Energy (kJ/mol)
Total Electrostatic Energy	41.25749	172.737
Total Van der Waal's Energy	2.82311
Total Out-of-Plane Bending Energy	24.68536
Total Torsional Energy	-1.65719
Total Stretch Bending Energy	-0.37839
Total Angle Bending Energy	0.00028
Total Bond Stretching Energy	10.6373
Total Energy	5.14702

Important electrostatic interaction lengths between the nucleophilic allylic carbons and electrophilic overhanging hydrogens are noted below, alongside important H-H Van der Waal's interaction lengths. Numbering of interaction lengths is made with respect to the figure below.

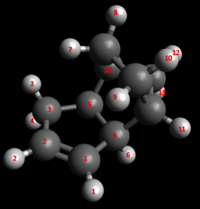
Electrostatic Interaction	Interaction Distance (Å)
C1-H4	2.666
C2-H3	3.206
C2-H4	3.159
C1-H3	3.471

H-H Van der Waal's Interaction	Interaction Lengths (Å)
H3/4-H5	2.285
H1-H6	2.674
H5-H14	2.459
H5-H13	2.518
H6-H13	2.632
H8-H12	2.609
H10-H12	2.572

The thermodynamic product of hydrogenation is dimer 4, which has a lower total energy. Van der Waal’s energy for product 4 is lower as only one H-H steric interaction lies within the repulsive region (<2.4 A, ^[2] and experimental observations.^[2]), c.f two steric clashes for product 3. Bond stretch, angle bending, out of plane bending and torsional energies are lower for product 4. Bend stretching energy is lower for product 3. Torsional energy is higher for dimer 3 as an eclipsed arrangement is forced upon the allyl group, with both allylic hydrogens arranged syn-periplanar with the X and Y hydrogens. In molecule 4, the hydrogens of the allylic group are in a staggered conformation with the bonded carbon hydrogens, which reduces steric clashing and increases σ-hyperconjugation, so lowering strain. These effects lower the bond stretch, angle bending and out of plane bending energies as less steric clashing is exhibited. Electrostatic energy of molecule 3 is lower than for molecule 4 as the distance between the partially negative, nucleophilic allylic carbons and the electrophilic overhanging hydrogens is reduced, so allowing for an increased interaction in molecule 3.

Conformations of an Intermediate in Taxol Synthesis

For both the carbonyl-up and the carbonyl-down atropisomer, four conformational isomers exist, which can be interconverted through a series of bond rotations. These conformational isomers occur due to the stereochemistry of the C ring, which has a cyclohexane structure and four energy minima: chair 1, twist-boat 1, twist-boat 2, chair 2 which are allowed by distortions of the cycloheptane B ring. The cycloheptane B ring has greater strain than cyclohexane C ring, partly due to transannular crowding (steric hindrance by groups on opposite sides of the ring). Thus to find the lowest energy conformation, the cyclohexane ring geometry need only be changed.
Considering only the cyclohexane ring, the planar structure was not trialled as it is well reported that with bond angles of 120º, (10.5º larger than the ideal angle of tetrahedral geometry) angle strain is too high. Additionally, every C-C bond in this structure would be eclipsed, resulting in high eclipsing strains and a highly destabilised structure. Of the reported energetically allowed confromers of the cyclohexane ring: chair; twist-chair; twist-boat and boat structures were trialled.
The highest energy conformer is reported to be the twist-chair form, which could not be modelled for either the atropisomers due to the global energy maximum lying at this geometry, between the two more favourable of the chair (a global minimum) and the twist-boat (local minimum) conformers.
The cyclohexane boat structure has two eclipsed bonds, with severed steric crowding of the "bow" and "stern" hydrogen atoms. As a result of these destabilising effects, which result in the bot form lying at the top of a local energy maxima between the two twist-boat froms, the cyclohexane C ring boat structure could not be found in either the carbonyl-up or carbonyl-down atropisomers.
By twisting the boat conformation, the steric hindrance of the boat is somewhat relieved. This allowed the two twist-boat conformers to be modelled for both atropisomers.
Lifting one carbon atom above the ring plane, and moving the other below ring planereduces the conformer energy further. This staggered structure conformer, in chair conformation, exists with the lowest energy, and is well-reported to exist as the dominant structure adopted by cyclohexane molecules. (REFERENCES: ORGANIC CHEM)

Carbonyl-down Atropisomers

Conformational Isomer	Conformer 1		Conformer 2		Conformer 3		Conformer 4		Conformer 5
Conformational Isomer	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)
B ring eclipsed, C ring chair 1	B ring eclipsed, C ring chair 60.55459 kcal/mol B ring eclipsed, C ring chair 60.55459 kcal/mol	Total Electrostatic Energy = -0.05161 Total Van der Waals = 33.22746 Total Out-of-Plane Bending Energy = 0.85124 Total Torsional Energy = 0.26085 Total Stretch Bending Energy = -0.14424 Total Angle Bending Energy = 18.81474 Total Bond Stetching Energy = 7.59616 Total Energy = 60.55459
B ring staggered, C ring chair 2	B ring staggered, C ring chair 74.97578 kcal/mol	Total Electrostatic Energy = 0.47721 Total Van der Waals = 35.62172 Total Out-of-Plane Bending Energy = 1.59809 Total Torsional Energy = 7.92190 Total Stretch Bending Energy = -0.21690 Total Angle Bending Energy = 21.18430 Total Bond Stetching Energy = 8.38944 Total Energy = 74.97578	B ring staggered, C ring chair 74.89187 kcal/mol	Total Electrostatic Energy = 0.45760 Total Van der Waals = 35.71917 Total Out-of-Plane Bending Energy = 1.61037 Total Torsional Energy = 7.60033 Total Stretch Bending Energy = -0.21462 Total Angle Bending Energy = 21.25908 Total Bond Stetching Energy = 8.45994 Total Energy = 74.89187	B ring staggered, C ring chair 70.70427 kcal/mol	Total Electrostatic Energy = 0.23104 Total Van der Waals = 35.22782 Total Out-of-Plane Bending Energy = 0.92455 Total Torsional Energy = -0.85820 Total Stretch Bending Energy = -0.15877 Total Angle Bending Energy = 27.10501 Total Bond Stretching Energy = 8.23281 Total Energy = 70.70427	B ring staggered, C ring chair 70.73128 kcal/mol	Total Electrostatic Energy = 0.22888 Total Van der Waals = 35.25229 Total Out-of-Plane Bending Energy = 0.92546 Total Torsional Energy = -0.92439 Total Stretch Bending Energy = -0.15213 Total Angle Bending Energy = 27.17449 Total Bond Stretching Energy = 8.22669 Total Energy = 70.73128	B ring staggered, C ring chair 70.67903 kcal/mol	Total Electrostatic Energy = 0.22795 Total Van der Waals = 35.27567 Total Out-of-Plane Bending Energy = 0.95955 Total Torsional Energy = -0.75685 Total Stretch Bending Energy = -0.16890 Total Angle Bending Energy = 26.99255 Total Bond Stretching Energy = 8.14905 Total Energy = 70.67903
B ring staggered, C ring twist-boat 1	B ring staggered, C ring twist boat 138.37778 kcal/mol	Total Electrostatic Energy = 1.91522 Total Van der Waals = 52.42341 Total Out-of-Plane Bending Energy = 2.76891 Total Torsional Energy = 7.67376 Total Stretch Bending Energy = -0.51417 Total Angle Bending Energy = 60.24160 Total Bond Stretching Energy = 13.86905 Total Energy = 138.37778	B ring staggered, C ring twist boat 138.43313 kcal/mol	Total Electrostatic Energy = 1.91704 Total Van der Waals = 52.14369 Total Out-of-Plane Bending Energy = 2.78293 Total Torsional Energy = 7.76965 Total Stretch Bending Energy = -0.49889 Total Angle Bending Energy = 60.52090 Total Bond Stretching Energy = 13.79780 Total Energy = 138.43313	B ring staggered, C ring twist boat 138.43466 kcal/mol	Total Electrostatic Energy = 1.91217 Total Van der Waals = 52.10441 Total Out-of-Plane Bending Energy = 2.73095 Total Torsional Energy = 7.59818 Total Stretch Bending Energy = -0.50455 Total Angle Bending Energy = 60.85561 Total Bond Stretching Energy = 13.73789 Total Energy = 138.43466	B ring staggered, C ring twist boat 65.82924 kcal/mol	Total Electrostatic Energy = 0.09374 Total Van der Waals = 35.38455 Total Out-of-Plane Bending Energy = 0.70011 Total Torsional Energy = 4.45351 Total Stretch Bending Energy = -0.02810 Total Angle Bending Energy = 17.43881 Total Bond Stretching Energy = 7.78661 Total Energy = 65.82924
B ring eclipsed, C ring twist-boat 2	B ring eclipsed, C ring higher energy twist-boat 75.03719 kcal/mol	Total Electrostatic Energy = 0.40144 Total Van der Waals = 35.79491 Total Out-of-Plane Bending Energy = 1.55287 Total Torsional Energy = 7.44715 Total Stretch Bending Energy = -0.20440 Total Angle Bending Energy = 21.52222 Total Bond Stretching Energy = 8.52300 Total Energy = 75.03719	B ring eclipsed, C ring higher energy twist-boat 68.88626 kcal/mol	Total Electrostatic Energy = -0.04523 Total Van der Waals = 34.66701 Total Out-of-Plane Bending Energy = 0.95110 Total Torsional Energy = 4.45092 Total Stretch Bending Energy = -0.06447 Total Angle Bending Energy = 21.08743 Total Bond Stretching Energy = 7.83950 Total Energy = 68.88626	B ring eclipsed, C ring higher energy twist-boat 66.32321 kcal/mol	Total Electrostatic Energy = -0.04537 Total Van der Waals = 35.08423 Total Out-of-Plane Bending Energy = 0.84920 Total Torsional Energy = 3.17749 Total Stretch Bending Energy = -0.05922 Total Angle Bending Energy = 19.57742 Total Bond Stretching Energy = 7.73947 Total Energy = 66.32321

The conformers, in order of increasing energy and decreasing stability are: chair 1, twist-boat 1, twist-boat 2, chair 2. The lowest energy conformer of the carbonyl-down atropisomer exists as the B ring eclipsed, C ring chair conformation with total energy of 60.55459 kcal/mol. Differences in energy between the optimised structures for each specified conformational isomer is mostly due to the cycloheptane B ring geometry, which can change dramatically with even minute geometry differences of a specified cyclohexane C ring conformer. This is due to increased complexity of the cycloheptane ring, allowing a wide array of geometries lying between two extremes of all-staggered C-C bonds and all-eclipsed C-C bonds. For simplicity here, all structures that did not appear with all-eclipsed bonds were tabulated with B ring staggered bonds.
The lowest energy carbonyl-down confomer exists with a cyclohexane C ring chair geometry, agreeing with literature. (REFERENCE ORGANIC CHEMISTRY) Of the two chair forms, termed chair 1 and chair 2, the lowest energy conformer, chair 1, has an eclipsed B ring structure, c.f. the staggered B ring of the higher energy conformer. This indicates that eclipsing interactions are not the only factor that needs to be considered, as an increase in eclipsing interactions should result in a higher energy conformer. All conformers have a strained gauche arrangement around the cyclohexane ring bridging C-C bond. However, the chair 1 form has a more regular gauche arrangement, as can be seen through dihedral angle analysis. The selected dihedral angles here are those involving the two ring bridging hydrogens, and are as summarised below.

Conformational Isomer	Torsion Angle H1-C-C-H2 (°)	Torsion Angle H1-C-C-C1 (°)	Torsion Angle H1-C-C-C2 (°)	Torsion Angle H2-C-C-C3 (°)	Torsion Angle H2-C-C-C4 (°)
B ring eclipsed, C ring chair 1	48.5	67	167	68.1	163.5
B ring staggered, C ring chair 2	52.9	62.4	168.1	59.2	174.1
B ring eclipsed, C ring twist-boat 1	33.2	88.3	153.5	90.5	35
B ring staggered, C ring twist-boat 2	28.9	86.6	147.4	86.3	142

The two chair forms give a more regular gauche arrangement than the twist boat forms, allowing for increasing overlap of σ-σ* orbitals in stabilising hyperconjugation. This effect thus contributes to the increased stabilisation of chair form 1.
Hyperconjugation interactions are summarised in the table below.

Conformational Isomer	*(C-C-(R) σ -> H-C σ)**	*(C-H σ -> C-C-(R) σ)**	*(C-H σ -> C-H σ)**	*(C-C σ -> C-C σ)**	*(C-C-(OR) σ -> C-H σ)**	*(H-C σ -> C-C-(OR) σ)**	*(C-C-(OR) σ -> C-C σ)**	*(C-C σ -> C-C-(OR) σ)**
B ring eclipsed, C ring chair 1	1	1	0	2	1	1	0	O
B ring staggered, C ring chair 2	2	2	0	0	0	0	1	1
B ring eclipsed, C ring twist-boat 1	0	0	2	2	0	0	1	1
B ring staggered, C ring twist-boat 2	1	1	0	2	1	1	0	0

As C is more electronegative than H (χ^P 2.5 c.f 2.1 respectively), so the C–C σ* orbital is lower in energy than the C–H σ* orbital, giving a slightly more favourable hyperconjugative interaction between the C–H σ bond and the C–C σ* orbital compared to that between the C–H σ bond and the C–H σ* orbital (1.5 kcal/mol vs. 1.0 kcal/mol). ^[1] This effect is increased for the C-C-(R)-> C-C-(OR) σ* interaction, and even more so for the C-C-(OR) σ* -> C-C-(H) σ conjugation due to the increased χ^P of oxygen relative to carbon and hydrogen. The chair 1 form benefits from both additional stabilisation from the C-(H)σ -> C-C-(OR) σ* and C-H σ -> C-C σ* hyperconjugations, which contribute to the stabilisation of this conformer. The chair 2 conformer benefits from C-H σ -> C-C-(R) σ* and C-C σ -> C-C-(OR) σ* interactions, whilst the twist-boat 1 conformer benefits from C-C σ -> C-C-(OR) σ* conjugations and twist-boat 2 benefits from H-C σ -> C-C-(OR) σ* and C-H σ -> C-C-(R) σ* hyperconjugations. Considering only hyperconjugation effects, the twist-boat 1 would be expected to be less stable than chair 2 and twist-boat 2, with chair-2 being less stable than twist-boat 2. Put simply, using the hyperconjugation analysis, the conformers in theoretical order of increasing energy are: chair 1, twist-boat 2, chair 2, twist-boat 1.
Thus, as the observed energy order differs from that obtained through analysis of equatorial effects (hyperconjugation interactions) it is evident that significant steric hindrance occurs between the B ring carbonyl group and the downward projecting carbon atom of the chair 2 and twist-boat 2 conformers. A 2.757 A close contact interaction exists between the carbonyl-down oxygen and the downward projecting carbon of the chair 2 cylohexane ring. This steric interaction is not present for the chair 1, B eclipsed ring form, as the cyclohexane chair form present here is the mirror image of that present in the B staggered ring isomer, and so the equivalent cyclohexane carbon atom projects upwards. The favourable reduction in the carbonyl-cyclohexane chair steric interaction outweighs the destabilising eclipse strain present in the B-ring, and this is reinforced through analysis of the chair 2 and twist-boat conformers. Both twist-boat conformers would be expected to give a higher energy than both chair forms, considering cyclohexane effects only. However, as is tabulated above, both twist-boats give a lower, more stabilised energy than the chair 2 isomer. This indicates that the carbonyl-cyclohexane repulsive steric clash is the dominant repulsive interaction in the molecule, and is alleviated in the twist-boat forms due to increases in the oxygen-carbon distance by the rotation of the downward projecting cyclohexane carbon atom. The reduction in steric hindrance is greater than the increase in energy obtained from conformation conversion of the C ring from chair to twist-boat.
Twist-boat 2 is higher in energy than twist-boat 1 as, though the principal carbonyl-carbon steric repulsion of chair 2 form is reduced in both twist-boat isomers, twist-boat 2 results in a downward projecting carbon atom, at a distance of 3.128 A from the carbonyl oxygen. In twist boat 1, this carbon projects upwards, and the interaction is reduced due to the longer 4.232 A distance.
The B ring eclipsed, chair 1 form will be used in the following dithiol experimentation as this conformation is the most stable, and therefore will be observed as the predominant conformation. Additionally, the total taxol geometry of the lowest energy conformer is reinforced through comparison with literature, as this conformation was observed as the lowest energy conformation for a dithiol, methylated taxol derivative. ^[4]

ChemBio3D Optimisations

As a comparative aside, the twist-boat chair structures were trialled in ChemBio3D using the MMFF94 force field, a maximum of 500 iterations and an RMS gradient of 0.00000001. Results are as tabulated below.

Conformational Isomer	Conformer 1		Conformer 2
Conformational Isomer	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)
B ring eclipsed, C ring chair 1	B ring eclipsed, C ring chair 1 61.0278 kcal/mol	Total Energy = 61.0278	B ring eclipsed, C ring chair 1 60.5445 kcal/mol	Total Energy = 60.5445
B ring staggered, C ring chair 2	B ring staggered, C ring chair 2 70.6275 kcal/mol	Total Energy = 70.6275
B ring eclipsed, C ring twist-boat 2	B ring eclisped, C ring twist-boat 2 66.3100 kcal/mol	Total Energy = 66.3100

As for the minimisations performed in Avogadro, the B ring eclipsed, C ring chair 1 returns the lowest total energy, with a 0.00009 kcal/mol difference between the two programs and MMFF94s and MMFF94 force fields. The fit between the twist-boat 2 forms and the chair 2 forms using MMFF94 and MMF94s is similar, with differences of 0.01321 and 0.05153 kcal/mol respectively. All forms return lower energy using the MMFF94 force field. However, the energy distribution between the conformers is the same, with the chair 2 conformer is returned with higher energy than the twist-boat conformer with the MMFF94s force field, reinforcing the results obtained with the MMFF94s force field using Avogadro. This reinforces that the steric interaction between the carbonyl oxygen and the cyclohexane downward projecting carbon in chair form 2 is more repulsive than eclipsing interactions in the B ring obtained through alleviation of steric hindrance by upward rotation of the carbon atom to chair form, and to a reduced effect in the twist-boat 2 form.

Carbonyl-up Atropisomers

Carbonyl-up atropisomer conformations were trialed in the same method as the carbonyl-down atropisomer. The Taxol carbonyl-up atropisomer was modelled with each of the four cyclohexane ring conformations and the total energy minimised using the MMFF94s force field with conjugate gradients in Avogadro. To decrease the energy of each conformer further, atomic geometries were changed slightly prior to further minimisations using the MMF94s force field. The table below summarises a selection of the conformations trialed for each conformational isomer, with the lowest energy geometry for each isomer tabulated.

Conformational Isomer	Conformer 1		Conformer 2		Conformer 3		Conformer 4		Conformer 5		Conformer 6
Conformational Isomer	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)
B ring staggered, C ring chair 2	B ring staggered, C ring chair 131.2788231 kcal/mol	Total Electrostatic Energy = 1.62706 Total Van der Waals = 47.53841 Total Out-of-Plane Bending Energy = 2.40406 Total Torsional Energy = 6.67894 Total Stretch Bending Energy = -0.53556 Total Angle Bending Energy = 61.26476 Total Bond Stetching Energy = 12.30116 Total Energy = 131.2788231	B ring staggered, C ring chair 131.25834 kcal/mol	Total Electrostatic Energy = 1.59637 Total Van der Waals = 47.29274 Total Out-of-Plane Bending Energy = 2.38051 Total Torsional Energy = 6.46826 Total Stretch Bending Energy = -0.55717 Total Angle Bending Energy = 61.77266 Total Bond Stetching Energy = 12.30497 Total Energy = 131.25834	B ring staggered, C ring chair 131.26806 kcal/mol	Total Electrostatic Energy = 1.61176 Total Van der Waals = 47.44958 Total Out-of-Plane Bending Energy = 2.38811 Total Torsional Energy = 6.56152 Total Stretch Bending Energy = -0.54461 Total Angle Bending Energy = 61.50072 Total Bond Stetching Energy = 12.30099 Total Energy = 131.26806	B ring staggered, C ring chair 2 131.07731 kcal/mol	Total Electrostatic Energy = 1.50782 Total Van der Waals =46.74049 Total Out-of-Plane Bending Energy = 2.24378 Total Torsional Energy = 5.90459 Total Stretch Bending Energy = -0.56858 Total Angle Bending Energy = 62.89435 Total Bond Stetching Energy = 12.35487 Total Energy = 131.07731
B ring eclipsed, C ring chair 1	B ring eclipsed, C ring chair 1 123.41854 kcal/mol	Total Electrostatic Energy = 1.63300 Total Van der Waals = 44.46712 Total Out-of-Plane Bending Energy = 2.52423 Total Torsional Energy = 4.62418 Total Stretch Bending Energy = -0.16983 Total Angle Bending Energy = 57.91489 Total Bond Stetching Energy = 12.42495 Total Energy = 123.41854	B ring eclipsed, C ring chair 1 123.38535 kcal/mol	Total Electrostatic Energy = 1.63578 Total Van der Waals = 44.47899 Total Out-of-Plane Bending Energy = 2.53372 Total Torsional Energy = 4.70558 Total Stretch Bending Energy = -0.18453 Total Angle Bending Energy = 57.75445 Total Bond Stetching Energy = 12.46136 Total Energy = 123.38535	B ring eclipsed, C ring chair 1 123.37353 kcal/mol	Total Electrostatic Energy = 1.63629 Total Van der Waals = 44.50357 Total Out-of-Plane Bending Energy = 2.53751 Total Torsional Energy = 4.70787 Total Stretch Bending Energy = -0.17295 Total Angle Bending Energy = 57.69574 Total Bond Stetching Energy = 12.46551 Total Energy = 123.37353	B ring eclipsed, C ring chair 1 123.32868 kcal/mol	Total Electrostatic Energy = 1.63859 Total Van der Waals = 44.54910 Total Out-of-Plane Bending Energy = 2.56324 Total Torsional Energy = 4.95789 Total Stretch Bending Energy = -0.19997 Total Angle Bending Energy = 57.32752 Total Bond Stetching Energy = 12.52280 Total Energy = 123.32868	B ring eclipsed, C ring chair 1 123.32349 kcal/mol	Total Electrostatic Energy = 1.63955 Total Van der Waals = 44.57888 Total Out-of-Plane Bending Energy = 2.56823 Total Torsional Energy = 5.00947 Total Stretch Bending Energy = -0.20268 Total Angle Bending Energy = 57.23473 Total Bond Stetching Energy = 12.49530 Total Energy = 123.32349	B ring eclipsed, C ring chair 1 123.32320 kcal/mol	Total Electrostatic Energy = 1.63764 Total Van der Waals = 44.58146 Total Out-of-Plane Bending Energy = 2.56702 Total Torsional Energy = 4.99945 Total Stretch Bending Energy = -0.19687 Total Angle Bending Energy = 57.22484 Total Bond Stetching Energy = 12.50967 Total Energy = 123.32320
B ring eclipsed, C ring twist-boat 1	B ring eclipsed, C ring twist-boat 1 128.48151 kcal/mol	Total Electrostatic Energy = 1.66793 Total Van der Waals = 45.98552 Total Out-of-Plane Bending Energy = 2.53493 Total Torsional Energy = 7.45904 Total Stretch Bending Energy = -0.21728 Total Angle Bending Energy = 58.39814 Total Bond Stetching Energy = 12.65323 Total Energy = 128.48151	B ring eclipsed, C ring twist-boat 1 128.47502 kcal/mol	Total Electrostatic Energy = 1.65517 Total Van der Waals = 46.00742 Total Out-of-Plane Bending Energy = 2.53554 Total Torsional Energy = 7.39507 Total Stretch Bending Energy = -0.53549 Total Angle Bending Energy = 58.49646 Total Bond Stetching Energy = 12.58139 Total Energy = 128.47502	B ring eclipsed, C ring twist-boat 1 128.43682 kcal/mol	Total Electrostatic Energy =1.65472 Total Van der Waals = 46.03398 Total Out-of-Plane Bending Energy = 2.55088 Total Torsional Energy = 7.48060 Total Stretch Bending Energy = -0.19954 Total Angle Bending Energy = 58.31709 Total Bond Stetching Energy = 12.59909 Total Energy = 128.43682	B ring eclipsed, C ring twist-boat 1 128.43442 kcal/mol	Total Electrostatic Energy = 1.65733 Total Van der Waals = 46.03176 Total Out-of-Plane Bending Energy = 2.55578 Total Torsional Energy = 7.52936 Total Stretch Bending Energy = -0.20264 Total Angle Bending Energy = 58.20822 Total Bond Stetching Energy = 12.65461 Total Energy = 128.43442	B ring eclipsed, C ring twist-boat 1 128.40590 kcal/mol	Total Electrostatic Energy = 1.65531 Total Van der Waals = 46.02818 Total Out-of-Plane Bending Energy = 2.59326 Total Torsional Energy = 7.92157 Total Stretch Bending Energy = -0.23094 Total Angle Bending Energy = 57.76893 Total Bond Stetching Energy = 12.67129 Total Energy = 128.40590
B ring staggered, C ring twist boat 2	B ring staggered, C ring twist-boat 135.38221 kcal/mol	Total Electrostatic Energy = 1.61088 Total Van der Waals = 49.00052 Total Out-of-Plane Bending Energy = 2.28097 Total Torsional Energy = 9.14482 Total Stretch Bending Energy = -0.39447 Total Angle Bending Energy = 61.50182 Total Bond Stetching Energy = 12.23766 Total Energy = 135.38221	B ring staggered, C ring twist-boat 135.36156 kcal/mol	Total Electrostatic Energy = 1.60889 Total Van der Waals = 49.13997 Total Out-of-Plane Bending Energy = 2.24812 Total Torsional Energy = 9.04908 Total Stretch Bending Energy = -0.37416 Total Angle Bending Energy = 61.42617 Total Bond Stetching Energy = 12.26349 Total Energy = 135.36156	B ring staggered, C ring twist-boat 2 131.26806 kcal/mol	Total Electrostatic Energy = 1.61029 Total Van der Waals = 47.53394 Total Out-of-Plane Bending Energy = 2.36877 Total Torsional Energy = 6.51641 Total Stretch Bending Energy = -0.53549 Total Angle Bending Energy = 61.45503 Total Bond Stetching Energy = 12.32172 Total Energy = 131.27067	B ring staggered, C ring twist-boat 2 131.27409 kcal/mol	Total Electrostatic Energy = 1.62127 Total Van der Waals = 47.46346 Total Out-of-Plane Bending Energy = 2.40461 Total Torsional Energy = 6.64622 Total Stretch Bending Energy = -0.54107 Total Angle Bending Energy = 61.37870 Total Bond Stetching Energy = 12.30090 Total Energy = 131.27409	B ring staggered, C ring twist-boat 2 131.27882 kcal/mol	Total Electrostatic Energy = 1.62706 Total Van der Waals = 47.53841 Total Out-of-Plane Bending Energy = 2.40406 Total Torsional Energy = 6.67894 Total Stretch Bending Energy = -0.53556 Total Angle Bending Energy = 61.26476 Total Bond Stetching Energy = 12.30116 Total Energy = 131.27882	B ring staggered, C ring twist-boat 2 131.27441 kcal/mol	Total Electrostatic Energy = 1.62048 Total Van der Waals = 47.42292 Total Out-of-Plane Bending Energy = 2.40991 Total Torsional Energy = 6.65155 Total Stretch Bending Energy = -0.54446 Total Angle Bending Energy = 61.41411 Total Bond Stetching Energy = 12.29989 Total Energy = 131.27441

As indicated above, the conformations, in order of increasing energy are as follows:chair 1, twist-boat 1, chair 2, twist-boat 2. This complements the result of the carbonyl-up atropisomer, as for both configurations, the B ring eclipsed, C ring chair conformational isomer exists with lowest energy. As for the carbonyl-up atropisomer, this occurs through the combination of numerous effects, whihc include hyperconjugation and steric hindrance of the electron dense carbonyl oxygen. In order to rationalise electronic stabilisation by hyperconjugation, the summary table is shown below.

Conformational Isomer	*(C-C-(R) σ -> H-C σ)**	*(C-H σ -> C-C-(R) σ)**	*(C-C σ -> C-C σ)**	*(C-C-(OR) σ -> C-H σ)**	*(H-C σ -> C-C-(OR) σ)**	*(C-C-(OR) σ -> C-C σ)**	*(C-C σ -> C-C-(OR) σ)**
B ring eclipsed, C ring chair 1	1	1	2	1	1	0	0
B ring staggered, C ring chair 2	2	2	0	0	0	1	1
B ring eclipsed, C ring twist-boat 1	1	1	2	1	1	0	0
B ring staggered, C ring twist-boat 2	2	2	0	0	0	1	1

Considering hyperconjugation effects only, the chair 1 and twist-boat 1 conformers would be expected to lie at lower energy and be mores stable than the chair 2 and twist-boat 2 conformers. This is due to the chair and twist-boat 1 conformers obtaining the highly stabilising H-C σ -> C-C-(OR) σ* interaction, compared to the C-C σ -> C-C-(OR) σ* hyperconjugation present in the chair and twist-boat 2 conformers, which exerts a reduced stabilision due to the higher energy C-C σ orbital c.f. the C-H σ orbital, giving reduced overlap, and so weaker orbital interaction and reduced splitting energy with the low energy C-C-(OR) σ* orbital.
Further disparity between the conformers is partially due to steric interations with the bulky, electron dense carbonyl group of the B ring with the C ring carbons. These carbons are bulkier and more electronically dense than the ring hydrogens, which thus do not exert steric repulsions with the carbonyl electron cloud with as great a magnitude as do the carbon atoms. Steric clashing is reduced in the chair 1 isomer, as the eclipsed B ring geometry allows the cyclohexane ring to lie below the plane of the carbonyl, and so the upward projecting cyclohexane carbon, at 3.075 A, is too far away from the carbonyl oxygen to provide any substantial repulsion, whilst the upward projecting B ring carbon, at 4.556 A also does not provide significant steric hindrance. The twist boat 1 form exerts a roughly equivalent steric repulsion through the upward projecting B ring and C ring atoms lying at 4.551 A and 3.056 A from the carbonyl oxygen respectively. The carbonyl steric repulsions present in chair 2 form are increased compared to those present in the chair 1 and twist-boat 1 forms, due to an increase in the number of upward projecting carbon atoms in the B and C rings at close proximity to the carbonyl oxygen. These interactions are roughly equivalent to those present in twist-boat 2 form. In chair 2 form, the C and B ring upward projecting carbons lie at 4.522 and 3.323 A from the carbonyl oxygen. c.f the shorter 4.419 and 3.421 A distances between oxygen and the C and B ring carbons, present in twist-boat 1.
Thus, as both steric effects and hyperconjugation interactions give a roughly equivalent energy for the chair 1, twist-boat 1 and chair 2, twist-boat 2 pairs, the increased stabilisation of each chair form relative to the twist-boat conformers results from the inherent stability of the chair conformation, by virtue of reduced eclipsing interactions and increased σ-σ* overlap, allowing for stronger hyperconjugation interactions.

Comparison of Carbonyl-Up and Carbonyl-Down Atropisomers

The lower energy conformation is the carbonyl-down atropisomer, which at 60.55459 kcal/mol is almost twice as stable as the lowest energy 123.3232 kcal/mol conformation of the carbonyl up atropisomer. Both structures feature a chair C ring, which is energetically favourable and locked into place by the centrally positioned bridge E-cyclononenone , which features heightened non-bonded trans-annular interactions than for the staggered B ring conformers, as has been reported. ^[5] The lower energy of the carbonyl-down isomer arises from the vast reduction in carbonyl oxygen cyclohexane carbon steric hindrance, which cannot be achieved in the carbonyl-up configuration. As thermodynamically, the final molecule in the oxy-cope equilibrium (carbonyl-up atropisomer) is higher and more unstable than the reagent and first carbonyl-down atropisomer product, this allows for the establishment of an observable equilibrium by the principle of microscopic reversibility.^[5] The carbonyl-down atropisomer is an example of a hyperstable olefin, a set of olefins which are stabilised rather than destabilised because of their bridgehead location and are unreactive. Poly-cyclic rings magnify the effects of hyperstability due to the stability gained by the olefin cage structure and the parent poly-cycloalkane being more strained.^[6] A selection of successive energy mimisations, achieved using the MMFF94s force field and conjugate gradient algorithm in Avogadro, of the cage structure in question, a bicyclo [6.2.1]undec-1-ene, is tabulated below, and reveals that Oxy-Cope Rearrangement stabilises the molecule from 85.54366 kcal/mol to 60.53455 kcal/mol at the MMFF94s level of theory. The lowest obtained pre-Oxy-Cope geometry and the stabilisation gained upon Oxy-Cope Rearrangement are in accordance with results documented by Paquette et al.^[5]

Taxol Pre-oxy Cope Rearrangement
Conformer 1		Conformer 2		Conformer 3
Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)
Taxol pre-Oxy Cope Rearrangement minimised to 94.80472 kcal/mol	Total Electrostatic Energy = 19.29532 Total Van der Waals = 38.64676 Total Out-of-Plane Bending Energy = 0.04770 Total Torsional Energy = -3.11166 Total Stretch Bending Energy = -1.45139 Total Angle Bending Energy = 29.29113 Total Bond Stetching Energy = 12.08687 Total Energy = 94.80472	Taxol pre-Oxy Cope Rearrangement minimised to 85.54372 kcal/mol	Total Electrostatic Energy = 16.34218 Total Van der Waals = 37.35729 Total Out-of-Plane Bending Energy = 0.03619 Total Torsional Energy = -3.77616 Total Stretch Bending Energy = -1.47038 Total Angle Bending Energy = 26.31645 Total Bond Stetching Energy = 10.73814 Total Energy = 85.54372	Taxol pre-Oxy Cope Rearrangement minimised to 85.54366 kcal/mol	Total Electrostatic Energy = 16.34231 Total Van der Waals = 37.35759 Total Out-of-Plane Bending Energy = 0.03606 Total Torsional Energy = -3.77637 Total Stretch Bending Energy = -1.46992 Total Angle Bending Energy = 26.31525 Total Bond Stretching Energy = 10.73874 Total Energy = 85.54366

As is the requirement for hyperstable olefins, the parent alkane of the carbonyl-down atropisomer, at 69.5350 kcal/mol using the MMFF94s force field, is higher in total energy than the carbonyl-down olefin, at 60.53445 kcal/mol using the same level of theory and force field.^[6]

Taxol Hydrogenation Product
Conformer 1		Conformer 2		Conformer 3
Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)
Taxol Hydrogenation Product minimised to 69.54399 kcal/mol	Total Electrostatic Energy = 0.00000 Total Van der Waals = 31.24484 Total Out-of-Plane Bending Energy = 0.03592 Total Torsional Energy = 9.27390 Total Stretch Bending Energy = 0.29445 Total Angle Bending Energy = 22.29051 Total Bond Stetching Energy = 6.40437 Total Energy = 69.54399	Taxol Hydrogenation Product minimised to 69.54357 kcal/mol	Total Electrostatic Energy = 0.00000 Total Van der Waals = 31.21907 Total Out-of-Plane Bending Energy = 0.03469 Total Torsional Energy = 9.18404 Total Stretch Bending Energy = 0.29428 Total Angle Bending Energy = 22.40441 Total Bond Stretching Energy = 6.40707 Total Energy = 69.54357	Taxol Hydrogenation Product minimised to 69.53530 kcal/mol	Total Electrostatic Energy = 0.00000 Total Van der Waals = 31.28088 Total Out-of-Plane Bending Energy = 0.03615 Total Torsional Energy = 9.20654 Total Stretch Bending Energy = 0.29431 Total Angle Bending Energy = 22.29783 Total Bond Stetching Energy = 6.41958 Total Energy = 69.53530

This reinforces the stability of the olefin and the elongated time required for the oxy-cope rearrangement, the product of which is higher in energy than the parent carbonyl-down olefin, as documented above. ^[5]

Dithiol, Methylated Derivative of Taxol

The lowest energy conformer for taxol, the carbonyl-down, B=eclipsed C=chair isomer, was used as a "starting block" for the dithiol, methylated taxol derivative, drawn using the appropriate tools in Avogadro and minimised using the MMFF94s force field with conjugate gradients in Avogadro. This gave two conformers based on the slope of the dithiol ethylene group. Results are noted below.

Conformational Isomer	Conformer 1		Conformer 2		Conformer 3
Conformational Isomer	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)
B ring eclipsed, C ring chair, dithiol slope right to left	taxol dithiol derivative, carbonyl down, eclipsed, chair, higher energy dithiol conformer	Total Electrostatic Energy = -6.01552 Total Van der Waals = 49.26889 Total Out-of-Plane Bending Energy = 0.89120 Total Torsional Energy = 9.65702 Total Stretch Bending Energy = 0.65716 Total Angle Bending Energy = 31.08724 Total Bond Stetching Energy = 14.96419 Total Energy = 100.51019	taxol dithiol derivative, carbonyl down, eclipsed, chair, lower energy dithiol conformer 100.49638 kcal/mol	Total Electrostatic Energy = -6.04364 Total Van der Waals = 49.35210 Total Out-of-Plane Bending Energy = 0.89469 Total Torsional Energy = 9.65981 Total Stretch Bending Energy = 0.65065 Total Angle Bending Energy = 30.98398 Total Bond Stetching Energy = 14.99878 Total Energy = 100.49638		Total Electronic Energy = 5.07403 Total Van der Waals = 19.97645 Total Out-of-Plane Bending Energy = 0.02967 Total Torsional Energy = 1.01202 Total Stretch Bending Energy = -0.80469 Total Angle Bending Energy = 2.61375 Total Bond Stetching Energy = 2.78242 Total Energy = 30.68364
B ring eclipsed, C ring chair, dithiol slope left to right	Dithiol taxol derivative, B ring eclipsed, C ring chair, dithiol slope left to right 100.45058 kcal/mol	Total Electronic Energy = -6.01409 Total Van der Waals = 49.27260 Total Out-of-Plane Bending Energy = 0.88841 Total Torsional Energy = 9.65287 Total Stretch Bending Energy = 0.63018 Total Angle Bending Energy = 30.94874 Total Bond Stretching Energy = 15.07185 Total Energy = 100.45058		Total Electronic Energy = 5.15300 Total Van der Waals = 19.37922 Total Out-of-Plane Bending Energy = 0.00939 Total Torsional Energy = 1.67403 Total Stretch Bending Energy = -0.86951 Total Angle Bending Energy = 2.18029 Total Bond Stretching Energy = 2.69798 Total Energy = 30.22440

This was optimised further to give a lower energy conformation of this isomer. taxol dithiol derivative, carbonyl down, eclipsed, chair, higher energy dithiol conformer

Type of Energy Contribution	Energy (kcal/mol)
Total Electrostatic Energy	-6.00757
Total Van der Waal's Energy	38.80345
Total Out-of-Plane Bending Energy	0.88053
Total Torsional Energy	9.67023
Total Stretch Bending Energy	0.67389
Total Angle Bending Energy	30.97644
Total Bond Stretching Energy	14.98488
Total Energy

‎

Second Conformer (lower energy)

The lower energy conformer has a geometry in agreement with literature. ^[1]

NEED DATA FOR THIS

This structure was optimised to a lower energy conformer.

taxol dithiol derivative, carbonyl down, eclipsed, chair, lower energy dithiol conformer

Type of Energy Contribution	Energy (kcal/mol)
Total Electrostatic Energy	-6.01409
Total Van der Waal's Energy	38.75358
Total Out-of-Plane Bending Energy	0.88842
Total Torsional Energy	9.65288
Total Stretch Bending Energy	0.63018
Total Angle Bending Energy	30.9487
Total Bond Stretching Energy	15.07189
Total Energy	89.93156

To check that the B=envelope, C=chair conformer was a minimum for the dithiol, methylated taxol derivative, a number of other isomers were tested, and documented below.

Conformational Isomer	Conformer 1		Conformer 2		Conformer 3
Conformational Isomer	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)
B ring staggered, C ring chair, dithiol slope right to left	taxol dithiol derivative, carbonyl down, eclipsed, twist-boat, dithiol conformer 102.35566 kcal/mol	Total Electrostatic Energy = -7.63857 Total Van der Waals = 51.72894 Total Out-of-Plane Bending Energy = 1.23175 Total Torsional Energy = 10.70883 Total Stretch Bending Energy = 0.01332 Total Angle Bending Energy = 31.07099 Total Bond Stetching Energy = 15.24039 Total Energy = 102.35566
B ring eclipsed, C ring boat, dithiol slope left to right	taxol dithiol derivative, B ring eclipsed, C ring boat, dithiol left to right 102.28425 kcal/mol	Total Electrostatic Energy = -6.24643 Total Van der Waals = 50.49824 Total Out-of-Plane Bending Energy = 1.02534 Total Torsional Energy = 13.59904 Total Stretch Bending Energy = 0.48338 Total Angle Bending Energy = 28.52666 Total Bond Stetching Energy = 14.39801 Total Energy = 102.28425
B ring eclipsed, C ring twist-boat, dithiol slope left to right	B ring eclipsed, C ring twist-boat, dithiol left to right 102.58219 kcal/mol	Total Electrostatic Energy = -8.72989 Total Van der Waals = 52.55376 Total Out-of-Plane Bending Energy = 0.98243 Total Torsional Energy = 13.09340 Total Stretch Bending Energy = 0.31291 Total Angle Bending Energy = 28.88162 Total Bond Stetching Energy = 15.48796 Total Energy = 102.58219	B ring eclipsed, C ring twist-boat, dithiol slope left to right	B ring eclipsed, C ring twist-boat, dithiol left to right 102.31850 kcal/mol	Total Electrostatic Energy = -8.72989 Total Van der Waals = 52.55376 Total Out-of-Plane Bending Energy = 0.98243 Total Torsional Energy = 13.09340 Total Stretch Bending Energy = 0.31291 Total Angle Bending Energy = 28.88162 Total Bond Stetching Energy = 15.48796 Total Energy = 102.31850

NMR Analysis of dithiol Taxol Derivative

Modelling the Sulphur bonded Carbon correction constant

The carbon shift correction for the ketone functionality was calculated using the provided formula in the script. The carbon shift correction for the sulphur bonded carbon was calculated using the method proposed by Braddock et al.^[7]

This involved using dimethylsulphide and methane as model NMR complexes, optimising these structures using the MMFF94s force field with conjugate gradient algorithm in Avodagro to total energies of 3.23095 and 0.02638 kcal/mol respectively, which are shown below.

DMS total energy 3.23095 kcal/mol

Methane total energy 0.02638 kcal/mol

These optimised structures were used as input to optimisation and NMR simulation calculations at the DFT B3LYP 6-31G(d,p) level of theory in Gaussian09. This returned optimised DMS and methane structures as shown below, where DMS numbering is documented.

DMS optimised to DFT B3LYP 6-31G(d,p) level of theory Methane optimised to DFT B3LYP 6-31G(d,p) level of theory The DMS and Methane ¹³C NMR spectra of the optimised DMS and methane structures are as shown.

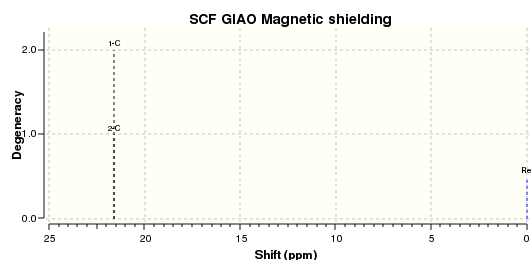
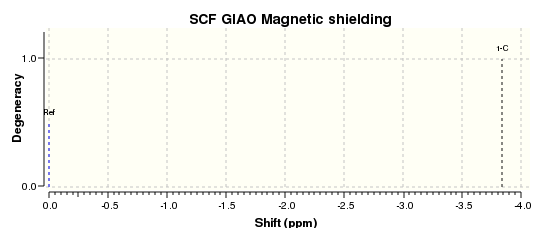
The carbon shift in dimethylsulphide was taken, and from this the methane carbon shift was subtracted, giving the sulphur correction. Parameters involved in this calculation are tabulated below.

Dimethylsulphide		Methane		δcorr (ppm)
Carbon Number	δcalc (ppm)	Carbon Number	δcalc (ppm)	δcorr (ppm)
C1	21.59386267	C1	-3.842204108	25.43606571
C2	21.59386054
Average	21.5938616

Analysis of Taxol Derivative NMR calculations

An initial NMR at B3LYP 6-31G(d) level of theory was run to compare with that obtained using B3LYP 6-31G(d,p) level of theory. This gave a structure of energy -1651.84055438 a.u, minimised to an RMS Gradient Norm = 0.00000896 a.u. and dipole moment of 1.8244 Debye.

Taxol,B ring eclipsed, chair 1 lowest energy conformer optimised to DFT B3LYP 6-31G(d) level of theory

The numbering of this structure used in ¹³C and ¹H NMR spectra analysis is shown below.

Atom numbering used in ¹³C and ¹H NMR spectrum analysis

Carbon and Hydrogen shifts are as noted.

¹³Carbon NMR			¹H NMR
Carbon Number	δcalc (ppm)	δcorr (ppm)	Hydrogen Number	δcalc (ppm)
C1	26.161857		H20	5.3808011259
C2	29.86709953		H18	2.1739491359
C3	147.5631791		H22	1.3884441820
C4	55.88038826		H23	2.0328648211
C5	39.98869248		H24	2.1101413932
C6	212.0205765		H25	1.5686530476
C7	55.208629		H26	1.5772279533
C8	121.0582038		H27	2.2212727976
C9	49.97235076		H28	1.1796658407
C10	24.56279499		H29	0.8114765715
C11	28.49392089		H30	0.5602421860
C12	33.98456806		H31	1.1097325593
C13	66.72226844		H32	0.5843857641
C14	92.90788938		H33	1.0914291282
C15	42.8563047		H34	0.5171291442
C16	25.65950574		H35	2.2921989860
C17	49.53367818		H36	2.3678804139
C19	35.59996883		H37	1.1055670964
C44	46.94962623		H38	0.8801533872
C45	45.28853047		H39	0.9134712328
			H40	1.9115711768
			H41	1.9390786429
			H42	1.5109610099
			H47	2.4266532587
			H49	2.3604387856
			H50	2.5928863775
			H51	1.7256286136
			H52	0.8754000000
			H53	0.2364156789

The hydrogen shifts are more removed from the experimental values than the carbon shifts. L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc.,, 1990, 112, 277-283. DOI:10.1021/ja00157a043 This is as expected as the two p-orbitals on hydrogen have not been taken into account at this level of theory.

The same molecule was entered into the NMR calculation again, using the expanded DFT B3LYP 6-31G(d,p) force field and basis set. These results, when compared with the 6-31G(d) basis set calculations gave a closer fit to the literature values, L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc.,, 1990, 112, 277-283. DOI:10.1021/ja00157a043 and those carbons bonded to sulphur and oxygen atoms were entered into sulphur and oxygen corrections. This gave results as follows.

¹³Carbon NMR
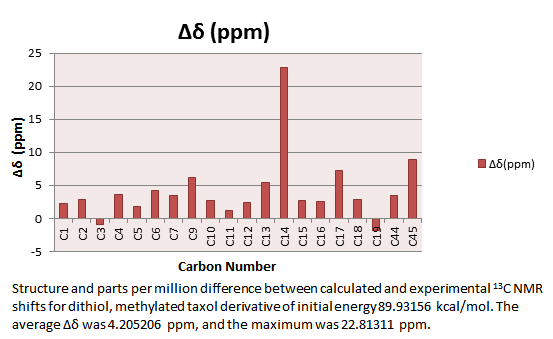
Carbon Number	δcalc (ppm)	δcorr (0.96δcalc + 12.2) (ppm)	Sulphur Correction (ppm)	δcorr (ppm)	∆δ(ppm)	Average ∆δ (ppm)
C1	24.45394017			24.45394017	2.243940174	4.20520568
C2	28.35963979			28.35963979	2.799639787
C3	147.8656084			147.8656084	-0.854391587
C4	54.93343559			54.93343559	3.633435588
C5	38.5101642			38.5101642	1.730164202
C6	211.9222905	215.6453988		215.6453988	4.155398844
C7	54.75635105			54.75635105	3.45635105
C9	49.5311262			49.5311262	6.251126196
C10	22.58014307			22.58014307	2.750143067
C11	26.50329918			26.50329918	1.153299184
C12	32.4674164			32.4674164	2.467416396
C13	65.93908338			65.93908338	5.40908338
C14	92.84098207		50.87213142	143.7131135	22.8131135
C15	41.47012634			41.47012634	2.740126336
C16	24.00755679			24.00755679	2.617556794
C17	48.03676504			48.03676504	7.216765045
C18	33.69603749			33.69603749	2.856037493
C19	33.69603749			33.69603749	-1.773962507
C44	45.64885345		25.43606571	71.08491916	3.525080837
C44	44.00772411		25.43606571	69.44378983	8.913789825

Part 2

Crystallographic Data

The structure of 21 (Shi asymmetric Fructose Catalyst), synthesised according to the scheme below

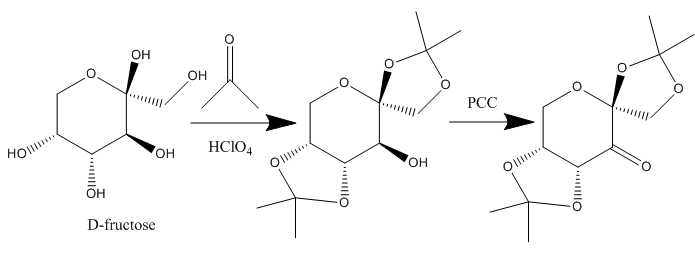
D-Fructose Shi catalyst synthesis scheme

was found in the Crystallographic Database using conquest, returning NELQEA

^[8] and NELQEA01^[9] structures, which were analysed using Mercury. An anomeric centre is a stereocentre resulting from intramolecular acetal (or ketal) formation of an aldehyde (or ketone) group and a hydroxyl group. Two stereochemistries at the anomeric centre are allowed, with each anomer being a diastereoisomers of the other.^[10] The α-anomer, with the anomeric substituent axial on the ring is stable and can exist as the dominant isomer over the β-isomer (anomeric substituent equatorial), depending on the other ring substituents. Considering steric arguments only, this is not the expected dominance as in chair conformation, bulky axial substituents cause destabilisation due to unfavourable 1,3-diaxial interactions. The anomeric effect may occur by stabilisation of the axial –OR via donation into the C-O σ* (antibonding) orbital by the lone pair of the pyranose ring oxygen. This hyperconjugation, a stereoelectronic effect acts against, and is observed over steric effects, which render axial -OR stereochemistry as repulsive. The anomeric effect increases in strength with the electronegativity of the anomeric substituent, thus for the OR group, the effect would be expected to be relatively strong in the Shi catalyst. It is reported that the anomeric effect is stronger in pyranose.^[11]

For analysis, all C-O bond lengths of the three acetal centres of the Shi catalyst were analysed. The pyranose ring acetal centre displayed bond lengths with a higher equivalence, whilst the acetal centres associated with the 2-dimethyl-(1,3)-dioxolane ring displayed the classical electronic stabilisation of the anomeric centre. This results in one C-O bond being significantly shorter than the other, due to the increase in bond strength of the ring C-O bond associated with π-like overlap of the oxygen p-orbital and the C-O σ*, and the decrease in bonding character of the C-O bond outside the ring, associated with electron donation from the oxygen into the C-O σ*.^[11]
The Shi fructose catalyst shows high enantioselectivity for the epoxidation of tri- and trans-substituted olefins. It has been reported that the pyranose oxygen is important for catalytic activity as electronically it inductively activates the carbonyl group to oxone attack due to the high electronegativity of the pyranose oxygen. ^[9] This effect is reinforced through analysis of the the pyranose ring C-O and 2,2-dimethyl-(1,3)-dioxolane ring C-O bond lengths, which have both axial orientations at the acetal carbon centre, so allowing for the double anomeric effect, where both C-O bonds are stabilised by the anomeric effect. ^[11]Assuming a double anomeric effect, with equivalent electron donation by each C-O axial lone pair into C-O σ*, one would expect equivalent bond lengths, as observed for molecule 1 in the NELQEA structure. However, NELQEA01 gives a longer 2,2-dimethyl-(1,3)-dioxolane ring C-O σ bond length, which may be indicative of the reported inductive electron withdrawal from the ketone by the pyranose oxygen. This effect increases the electron density of the pyranose C-O bond, increasing the bond strength and reducing bond length. An additional interaction between the ketone C=O π-cloud and 2,2-dimethyl-(1,3)-dioxolane ring C-O σ* bond may also be present, which may reduce electron density at the ketone further through the favourable π-like resonance effect between the C-O σ*-cloud and the C=O π-cloud, which is not present with the pyranose ring C-O bond.

The anomeric O-C-O bond lengths for each structure are noted below.

NELQEA

Shi catalyst crystal structure NELQEA

Molecule 1	'
Anomeric Centre bonds	Bond Length (A)
C7-01	1.413
C7-O2	1.441
C10-O5	1.409
C10-O4	1.439
Molecule 2
Anomeric Centre Bonds
C19-O7	1.38
C19-O8	1.443
C22-O11	1.416
C22-O10	1.438

Bond angles of the anomeric centres are as noted below.

Bond angle	Angle (theta)
Molecule 1
O1-C7-O2	103.2
O5-C10-O4	105.6
Molecule 2
O7-C19-O8	105.3
O10-C22-O11	105.1

Non-anomeric bonds and angles were analysed as below.

Non-anomeric bond lengths	Bond Length (A)
Molecule 1
C2-O6	1.403
C2-O2	1.403
Molecule 2
C14-O12	1.408
C14-O8	1.39

Bond angle	Angle (theta)
Molecule 1
O2-C2-O6	113.03
Molecule 2
O8-C14-O12	112.48

NELQEA01

This structure was analysed in the same way, with bond lengths and angles as tabulated below.

Shi catalyst crystal structure NELQEA01

'
Molecule 1
Anomeric Centre bonds	Bond Length (A)
C10-O5	1.428
C10-O4	1.456
C9-O1	1.423
C9-O2	1.454
Molecule 2
C22-O11	1.43
C22-O10	1.442
C21-O8	1.46
C21-O7	1.406

Bond angle	Angle (theta)
Molecule 1
O4-C10-O5	105.8
O1-C9-O2	103.6
Molecule 2
O11-C22-O10	105.7
O7-C21-O8	103

Non-anomeric bond lengths and angles are as noted in the following table.

Non-anomeric bond lengths	Bond Length (A)
Molecule 1
C2-O6	1.415
C2-O2	1.423
Molecule 2
C14-O8	1.42
C14-O12	1.405

Bond angle	Angle (theta)
Molecule 1
O8-C14-O12	113.26
Molecule 2
O6-C2-O2	112.78

The ketals are at both α-positions, and so act as chiral controls and activating groups. These ketals are sterically bulky enough and in close vicinity to the carbonyl group, allowing for high enantiomeric excess and reaction promotion at the carbonyl group. The lack of any R groups on the 5-membered rings reduces sterics around the carbonyl, allowing for oxone nucleophilic attack. ^[12]

Molecule 23,[Mn(III)(salen)(Cl)],(1R,2R)-(-)-[Bis(3,5-di-tert-butylsalicylidene)-1,2-cyclohexanediamine]chloromanganese(III), An Intermediate in Jacobsen's Catalyst Synthesis

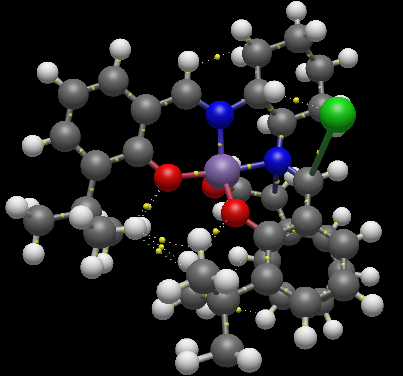
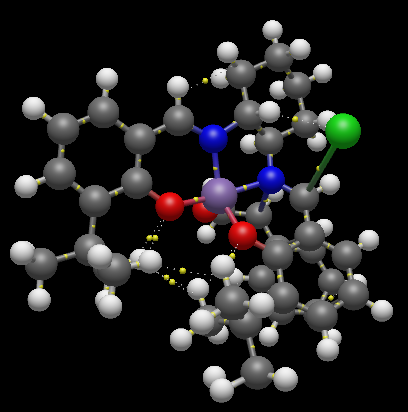
Two structures of the intermediate ([Mn(III)(salen)(Cl)]) to Jacobsen's catalyst were obtained, TOVNIB01 and TOVNIB02. These are as reported below.

TOVNIB01

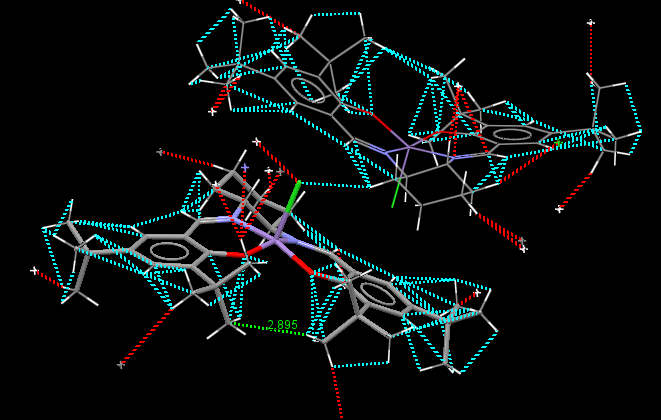
Jacobsen catalyst crystal structure TOVNIB01

TOVNIB02

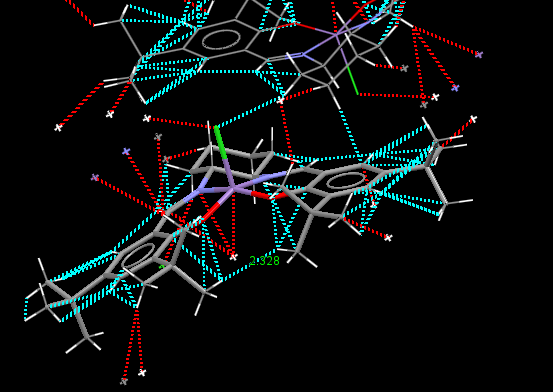
Jacobsen catalyst crystal structure TOVNIB02

Jacobsen’s ligand, (R,R)- or (S,S)-N,N′-bis(3,5-di-tert-butylsalicylidene)-1,2-cyclohexanediamine, (salen) contains a trans-cyclohexane-1,2-diamine linkage as the sole chiral unit. Salicylidene rings are each bonded to two sterically bulky tert-butyl groups. The enantiopure C2 symmetrical trans-cyclohexane-1,2-diamine serves as a sterodirecting group, creating chiral centres in substrate molecules. Previous X-ray crystal structural studies have shown that metal complexes of the salen ligand exist in an almost planar structure, with the tert-butyl groups of the salicylidene rings not being sufficiently sterically demanding to cause N₂O₂ coordination distortion. It has been reported that small deviations from planarity may however be required to predetermine the course of asymmetric reactions. ^[10] As is apparent from the crystal structures TOVNIB01 ^[13] and TOVNIB02^[14] documented, the N₂O₂ geometry exists with near planarity, indicating that the tert-butyl groups do not have sufficient steric bulk to cause distortion to a stepped geometry, as has been observed for similar Ni(II) complexes.^[10] Analysing the close contacts of the tert-butyl groups with the two Mn^(III) coordinated oxygens reveals that four interactions are made between each tert-butyl group and each oxygen. Two close contact interactions are made with attack from the chlorine side of the N₂O₂ coordination plane, with two close contact interactions between each tert-butyl and the oxygen from the under-side of this coordination plane. The tert-butyl groups have sufficient steric bulk to form four close contacts each with one phenyl functionality.

TOVNIB01

'

TOVNIB02

'

tBu-tBu Interactions

Attack from Cl-side

Attack from under Cl-side

Intramolecular Interactions

Interaction Distance (A)

Intramolecular Interactions

Average Interaction Distance (A)

Intramolecular Interactions

Interaction Distance (A)

Intramolecular Interactions

Average Interaction Distance (A)

Intramolecular Interactions

Average Interaction Distance (A)

TOVNIB01 (C-H, underside of Cl)

2.895

tBu(H)-O

2.193

tBu(C)-O

2.884

tBu(H)-O

2.55795

tBu(C)-O

3.017

TOVNIB02 (H-H, underside of Cl)

2.328

tBu(H)-O

2.335

tBu(C)-O

2.909

tBu(H)-O

2.497

tBu(C)-O

3.119

Analysis of the Transition State for Shi Catalyst Catalysed Epoxidation of Styrene

To find the styrene transition state in the Shi catalyst catalysed asymmetric epoxidation, the Gibbs free energy of the four transition states given for the R and S-isomers were analysed. This was carried out by accessing the .log file of each transition state structure, where the Gibbs Free Energy was found as the "Sum of Electronic and Thermal Free Energies". Results of the four R and four S-styrene oxide transition states are noted below.

R-styrene series	'	'	S-styrene series	'	'
Conformer DOI	Gibbs Free Energy (Hartree/Particle)	Gibbs Free Energy +Thermal Correction to Gibbs Free Energy(Hartree/Particle)	Conformer DOI	Gibbs Free Energy (Hartree/Particle)	Gibbs Free Energy + Thermal Correction to Gibbs Free Energy (Hartree/Particle)
10.6084/m9.figshare.822152	-1303.730703	-1303.34381	10.6084/m9.figshare.823545	-1303.73383	-1303.348909
10.6084/m9.figshare.828520	-1303.730238	-1303.344628	10.6084/m9.figshare.822136	-1303.72418	-1303.338169
10.6084/m9.figshare.822135	-1303.736813	-1303.35075	10.6084/m9.figshare.828519	-1303.72767	-1303.340216
10.6084/m9.figshare.822137	1303.738044	1304.124393	10.6084/m9.figshare.826003	-1303.73850	-1303.353713

This data reveals the structure with the lowest Gibb's Free Energy exists in the R-styrene oxide conformation, which was submitted for NCI and QTAIM analysis.

NCI and QTAIM Analysis of the S-styrene series

Non-covalent interactions refer to intra- and inter-molecular interactions that involve dispersed electromagnetic interactions and do not involve the sharing of electrons. ^[15] Such interactions are of the order of 1-5 kcal/mol. ^[15] Non-covalent interactions can be classified into four main categories: Van der Waals forces, π-effects, electrostatic,and hydrophobic effects. For the transition state of the Shi catalyst epoxidation of styrene, the R-styrene oxide conformation provides the lowest Gibb's Free Energy, a result supported by literature observation. ^[16] ^[17] ^[17] ^[17] Simply, this is due to non-covalent interactions in the transition state, which are greatest for the R-isomer product than for the S-isomer products, leading to the R-isomer pathway having a lower activation energy than the S-isomer pathway, which results in the R-isomer pathway being favoured and so having greater enantiomeric excess experimentally with the Shi catalyst. Both R and S-series transition states operate with a spiro conformation.

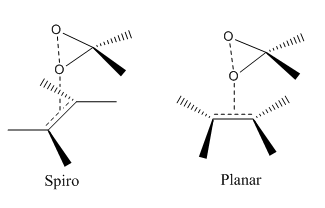
Spiro vs. planar epoxidation transition state

As illustrated below, the spiro A structure is observed for the transition states.

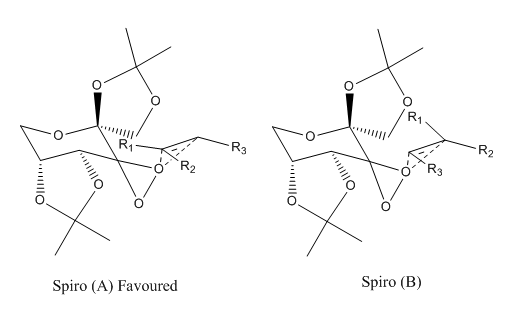
Spiro A vs. Spiro B epoxidation transition state

This result complies with literature, and this is favoured over the planar transition state due to the stabilising interaction of the dioxirane oxygen lone pair with the olefin pi* orbital. ^[17]

The S-styrene series NCI and QTAIM analysis results are as shown below. SM11 S isomer of styrene.cub.xyz

NCI analysis of the transition state for the Shi catalyst catalysed epoxidation towards the S-styrene oxide product 10.6084/m9.figshare.826003

[image:Screenshot NCI 3.PNG|centre|200px|frame|NCI analysis of the transition state for the Shi catalyst catalysed epoxidation towards the S-styrene oxide product 10.6084/m9.figshare.826003]]

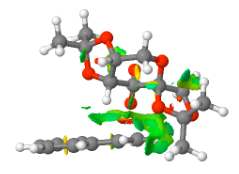
The S-styrene series transition state corresponding to 10.6084/m9.figshare.82600 of Gibbs Free Energy (without thermal correction constant) of -1303.73850 Hartree/Particle was also submitted to QTAIM analysis. Results are as below.

[[image:Qtaim 1.png|centre|200px|frame|Shi catalyst catalysed epoxidation of styrene 10.6084/m9.figshare.826003 S-series]

Shi catalyst catalysed epoxidation of styrene 10.6084/m9.figshare.826003 S-series

QTAIM and NCI analysis revealed the spiro transition state structure. This structure indicates significant C-O bond formation between the oxirane and C1 of the styrene ethyl substituent, which lies at an interaction distance of 1.969 Å, and as revealed by the NCI analysis, can be considered as "half-covalent". This spatial separation is greater than the C-O bond length of the oxirane, which lies at a distance of 1.414 Å and indicates incomplete product C-O bond formation, a conclusion reinforced by the product C-O bond lying at a distance greater than both the epoxide and the hydroxyl C-O typical bond length. The interaction between the β-carbon and the oxirane oxygen occurs over an increased distance of 2.349 Å, and the terminal hydrogen makes an interaction with the ketal oxygen with an interaction distance of 2.489 Å. Additional interactions between the ketal oxygen and the hydrogen at the β-carbon position lies at 2.572 Å. The ketal oxygen makes further interactions with the benzyl ring carbons with strongest interaction distances for each oxygen lying at 3.729 and 5.769 Å. The NCI analysis indicates two major attractive non-covalent interactions. One is intramolecular, and occurs between the eclipsed bonds of the benzene ring and the alkene C=C bond of styrene. The otehr is intermolecular and occurs between the alkene C=C bond of styrene and the oxygens of the dioxirane and the dioxacyclopentane ring which projects closest to the styrene C=C alkene bond.

R-styrene series QTAIM Lowest Energy Transition State

The lowest energy transition state of the Shi catalyst catalysed epoxidation reaction of styrene corresponded to the R-styrene oxide product pathway and was analysed by QTAIM analysis, which revealed the spiro transition state structure, as can be seen in the figures below.

Shi catalyst catalysed epoxidation of styrene lowest energy transition state R-series

This structure indicates significant C-O bond formation between the oxirane and C1 of the styrene ethyl substituent, which lies at an interaction distance of 1.998 Å. This spatial separation is greater than the C-O bond length of the oxirane, which lies at a distance of 1.423 Å and indicates incomplete product C-O bond formation on styrene but significant C-O bond breaking at the dioxirane, a conclusion reinforced by the product C-O bond lying at a distance greater than both the epoxide and the hydroxyl C-O typical bond length. The interaction between the β-carbon and the oxirane oxygen occurs over an increased distance of 2.349 Å, and the terminal hydrogen makes an interaction with the two ketal oxygens with interaction distances of 2.780 and 2.506 Å. Additional interactions between the ketal oxygen and the benzyl ring hydrogen lies at 2.915 and 4.194 Å. The hydrogen of the dioxacyclopentane interacts with the benzyl carbon at an interaction distance of 2.457 Å. The ketal oxygens make further interactions with the benzyl ring carbons with the strongest interaction distances for each oxygen lying at 3.491 and 5.523 Å, and it is these interactions, caused by better overlap of the benzyl ring with the dioxacyclopentane Shi catalyst ring which causes the R-styrene oxide product conformation to be favoured. The S-styrene oxide product pathway causes a significant reduction in the interactions between the benzyl functionality and the ketal oxygens due to the increase in spatial separation, thus causing the higher energies of the transition states for the S-styrene oxide product pathways. In summary, the R-styrene oxide product pathway is favoured as the transition state allows for reduced steric clashing between the bulky phenyl styrene ring and the Shi catalyst dioxacyclopentane ring at the 2-position on the pyranose ring. This also allows for increased interactions between the phenyl ring of styrene and the oxygens of the second dioxacyclopentane functionality at the 4-position on the pyranose ring of the Shi catalyst. Drawing from the NCI analysis of the higher energy S-styrene transition state, the favourable interactions here would be expected to arise between the alkene C=C bond and the oxygens of the dioxirane and dioxacyclopentane, and between the alkene C=C bond and the eclipsed benzene bonds. As the eclipsed benzene-alkene C=C interactions are available to the oxygens of the dioxirane and the dioxacyclopentane, this allows for an increased favourability of interaction for the R-series as the benzene ring is closer to the oxygens of the Shi catalyst, allowing for extended benzene pi-conjugation with the dioxirane and the dioxacyclopentane orbitals of the Shi catalyst. This conclusion is in accord with literature, which reports an attractive interaction between the oxazolidinone moiety of the Shi catalyst and styrene benzyl-π group in the transition state giving the spiro A transition state.^[18] Such non-covalent dispersive interactions have been previously reported to influence the stereoselectivity of reactions subject to enantiomeric differentiation.^[19]

Analysis of the Transition State for Jacobsen's Catalyst Catalysed Epoxidation of Styrene

The Gibb's Free Energy of each diastereomeric transition state was found from the .log file, with application of the thermal correction to free energy, giving result tabulated below.

R-styrene series	'	'	S-styrene series	'	'
Conformer DOI	Gibbs Free Energy (Hartree/Particle)	Gibbs Free Energy +Thermal Correction to Gibbs Free Energy(Hartree/Particle)	Conformer DOI	Gibbs Free Energy (Hartree/Particle)	Gibbs Free Energy + Thermal Correction to Gibbs Free Energy (Hartree/Particle)
10.6084/m9.figshare.860441	-3343.9691970	-3343.3060230	10.6084/m9.figshare.860446	-3343.960889	-3343.297060
10.6084/m9.figshare.860445	-3343.9631910	-3343.2987320	10.6084/m9.figshare.860449	-3343.962162	-3343.297940

This analysis revealed that the lowest energy transition state occurred for the R-series, a conclusion supported by literature, ^[20] ^[21] ^[22] and so this transtition state, which corresponds to the cis-breakdown pathway of the radical intermediate shown below, was used in QTAIM analysis.

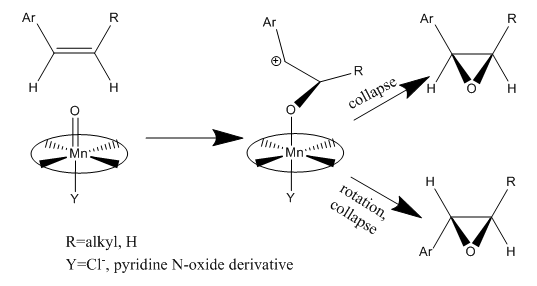
Jacobsen's catalyst radical intermediate breakdown pathway

S-styrene series QTAIM Lowest Energy Transition State

Jacobsen's catalyst catalysed epoxidation of styrene lowest energy transition state S-series

The S-series transition state indicated the significant formation of the C–O bond between the terminal carbon of the ethyl styrene substituent and the (salen)Mn-O oxygen. The C-O bond, at 1.779 Å is greater in length than the Mn-O bond which lies at 1.594 Å. The typical C-O bond length found in hydroxyl bonds lies at 1.43 Å , and 1.47 Å for epoxide C-O bonds. <refname="ja98253389760782">R. C Weast, Handbook of Chemistry and Physics, CRC Press, 65th Edition, 1984 Template:ISBN</ref> As the C-O interaction distance present in the transition is much greater than either of such bond lengths, it can be deduced that C-O bond formation in the transition state is not complete at C1. The β-carbon is oriented by the salen ligand oxygen, with an interaction distance of 3.054 Å. Additionally, the transition state is stabilised by π-overlap between the parallel displaced phenyl functionalities of styrene and the salen ligand, which are oriented with two strong interactions at distances of 3.290 and 3.388 Å.

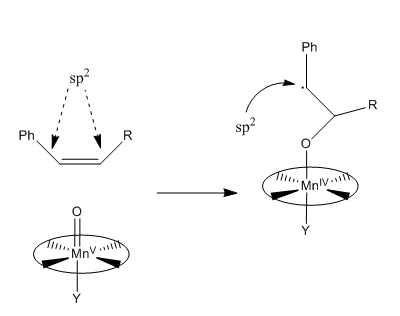
R-styrene series QTAIM Lowest Energy Transition State

Jacobsen's catalyst catalysed epoxidation of styrene lowest energy transition state R-series

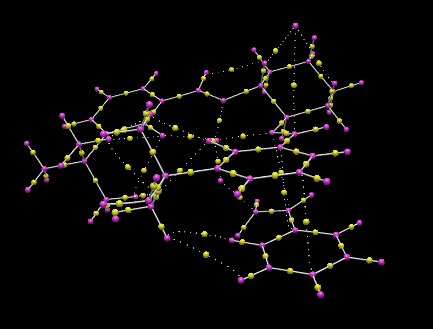
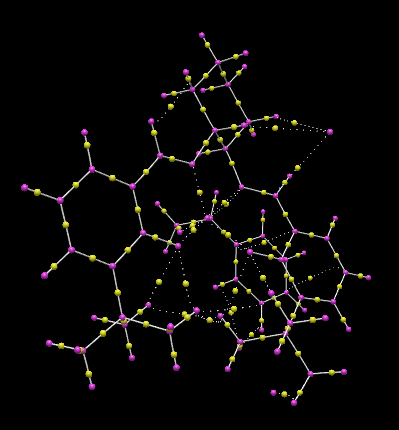
The lowest energy transition state of the Jacobsen’s catalyst catalysed epoxidation reaction of styrene, corresponded to the R-product pathway, and was analysed using QTAIM analysis. This agrees with literature reports carried out with [(R,R)-(–)-N,N-bis(3,5-di-tert-butylsalicylidene)-1,2-cyclohexanediaminomanganese(III) chloride]((R,R)-Jacobsen's catalyst). <refname="ja7696574643">J. Cubillosa, W. Hölderich, Rev. Fac. Ing. Univ. Antioquia, 2007,41, 31-47Template:ISSN</ref> This indicated the significant formation of the C–O bond between the terminal carbon of the ethyl styrene substituent and the (salen)Mn-O oxygen. The C-O bond, at 1.803 Å is greater in length than the Mn-O bond which lies at 1.592 Å. The typical C-O bond length found in hydroxyl bonds lies at 1.43 Å, and 1.47 Å for epoxide C-O bonds. <refname="ja98253389760782">R. C Weast, Handbook of Chemistry and Physics, CRC Press, 65th Edition, 1984 Template:ISBN</ref> As the C-O interaction distance present in the transition is much greater than either of such bond lengths, it can be deduced that C-O bond formation in the transition state is not complete at C1. The β-carbon is oriented by the salen ligand oxygen, with an interaction distance of 3.054 Å. Additionally, the transition state is stabilised by π-overlap between the eclipsed phenyl functionalities of styrene and the salen ligand, which are oriented with two strong interactions at distances of 3.294 and 3.421 Å. The eclipsed benzyl functionalities have an increased spatial separation in the R-styrene oxide product pathway conformation, but have increased overlap of π–clouds as in the S-series transition states, the benzyl rings exhibit parallel displacement, and so reduced stabilisation. Thus the S-styrene oxide product transition states exist at higher energies than the transition states for the R-styrene oxide pathways, disfavouring the S-styrene oxide product at low temperatures and inducing the enantioselectivity for the R-Styrene oxide in the Jacobsen’s catalyst catalysed epoxidation. Additionally, the side-on approach of the Mn=O bond with the styrene oxide is as reported in previous studies, Heterogeneous asymmetric epoxidation of cis-ethyl cinnamte over <refname="ja053389760782">J. A. C. Lobo, Jacobsen’s catalyst immobilized in inorganic porous materials, El Bagre, Kolumbien, 2005</ref> and it can be seen that the non-planarity of the salen-Mn bonding plane reported previously is present in the lowest energy transition state.

Analysis of the Transition State for Shi Catalyst Catalysed Epoxidation of 1,2-Dihydronapthalene

The Gibb's Free Energy of each diastereomeric transition state was found from the .log file, with application of the thermal correction to free energy. This revealed that the lowest energy transition state occurred for the S,R-series, and this was used in QTAIM analysis.

R,S-series	'	'	S,R-series	'	'
Conformer DOI	Gibbs Free Energy (Hartree/Particle)	Gibbs Free Energy +Thermal Correction to Gibbs Free Energy(Hartree/Particle)	Conformer DOI	Gibbs Free Energy (Hartree/Particle)	Gibbs Free Energy + Thermal Correction to Gibbs Free Energy (Hartree/Particle)
DOI:10.6084/m9.figshare.832492	-1381.120782	-1,380.697745	DOI:10.6084/m9.figshare.832538	-1381.131343	-1380.709885
DOI:10.6084/m9.figshare.832510	-1381.125886	-1,380.704512	DOI:10.6084/m9.figshare.832536	-1381.116109	-1380.696143
DOI:10.6084/m9.figshare.832511	-1381.134059	-1,380.711914	DOI:10.6084/m9.figshare.832545	-1381.126039	-1380.704465
DOI:10.6084/m9.figshare.832512	-1381.126722	-1,380.703543	DOI:10.6084/m9.figshare.832544	-1381.136239	-1380.714346

S,R-Dihydronapthalene oxide series QTAIM Highest Energy Transition State

QTAIM analysis of highest energy 1,2-dihydronapthalene oxide transition state DOI:10.6084/m9.figshare.832536

The transition state of the highest energy S,R-series Shi catalyst epoxidation of 1,2-dihydronapthalene corresponds to the S,R-product pathway. QTAIM analysis allows visualisation of the spiro transition state structure and significant C-O bond formation between the oxirane and C10 of the olefinic bond, which lies at a distance of 2.069 Å. The oxirane oxygen lies at an increased distance of 2.190 Å from C9, which lies closer to the benzyl functionality. QTAIM analysis further reveals the formation of strong interactions between ketal oxygen and the hexane-benzene bridging carbon, which lies at an interaction distance of 3.495 Å, and a much weaker interaction over a distance of 4.826 Å with the C3 ring bridging carbon and the ketal oxygen. Both of these interactions likely involve the overlap between the benzyl π-cloud and oxygen p-orbital lone pairs. A weaker interaction occur between the axial hydrogen of C1 and the pyranose ring oxygen at an interatomic distance of 2.088 Å and a further interaction exists between the C3 ring bridging carbon and the pyranose ring equatorial hydrogen separated by a spatial distance of 2.858 Å. For the transition states corresponding to the R,S-conformation, these interactions are reduced, as the available C1 hydrogen points equatorial, and is thus spatially further from the pyranose oxygen. Additionally, the benzyl group lies beneath the dioxacyclopentane ring at the 2-position on the pyranose. This ring projects down towards the benzyl group, but with the dioxacyclopentane carbon making the closest interaction with the benzyl group of 1,2-dihydronapthalene. This reduces the favourability of this orientation as the carbon lacks p-orbital lone pairs with which it can use to interact with the benzyl π-cloud.

S,R-Dihydronapthalene oxide series QTAIM Lowest Energy Transition State

QTAIM analysis of highest energy 1,2-dihydronapthalene oxide transition state DOI:10.6084/m9.figshare.832536

QTAIM analysis of lowest energy transition state

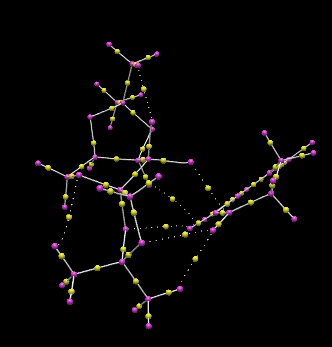
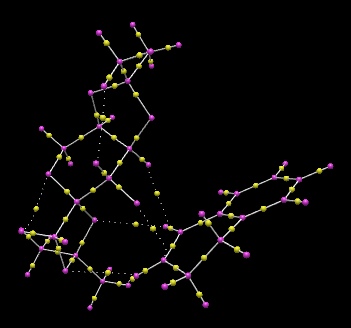
The transition state of lowest Gibb’s free energy of the Shi catalyst epoxidation of 1,2-dihydronapthalene corresponds to the S,R-product pathway, with an endo-structure between the phenyl functionality of the 1,2-dihydronapthalene reagent and the dioxyacyclopentane oxygen of the Shi catalayst. QTAIM analysis allows visualisation of the spiro transition state structure and significant C-O bond formation between the oxirane and C10 of the olefinic bond, which are spatially separated by 2.067 Å. The strong interaction here is due to the upward projection of the C1-C10 bond towards the dioxirane oxygen, increasing availability of the olefinic carbon for attack. The hydrogen of C1 is involved in a hydrogen-bonding like interaction with one oxygen of the dioxyacyclopentane at the C2-position on the pyranose ring, and a Van der Waals radii favourable overlap interaction with the dioxyacyclopentane methyl group. These interactions occur over distances of 2.445 and 2.233 Å respectively. The other dioxyacyclopentane oxygen is involved in an interaction with the other olefinic hydrogen at an interaction distance of 2.496 Å. The dioxirane oxygen lies at an increased distance of 2.189 Å from C9 c.f C10. QTAIM analysis further reveals the formation of strong interactions between ketal oxygen and the hexane-benzene bridging carbon, which lies at an interaction distance of 3.879 Å, and a much weaker interaction over a distance of 5.912 Å with the C3 ring bridging carbon and the other dioxyacyclopentane oxygen. Both of these interactions likely involve the overlap between the benzyl π-cloud and oxygen p-orbital lone pairs. A weaker interaction occur between the axial hydrogen of C2 and the dioxirane oxygen not involved in the epoxide formation, with an interatomic distance of 3.719 Å. For the transition state corresponding to the highest energy S,R-product, with the opposite direction of C10-C1 bond slope, the carbon involved in initial C-O bond formation with the dioxirane points downwards away from the dioxirane oxygen, reducing the interaction with the dioxirane oxygen due to an increased interaction distance of 2.069 Å. Additionally, the formation of the epoxide C-O bond occurs with the other dioxirane oxygen, which reduces steric clashing between the aromatic group of 1,2-dihydronapthalene oxide and the Shi catalyst dioxyacyclopentane rings, and allows for increase electrostatic interactions between the olefin and the dioxyacyclopentane oxygens.

NMR and Modelling of Alkenes and the Associated Epoxides

The two alkenes, and their corresponding epoxides chosen for molecular modelling were styrene (2-phenyloxirane) and 1,2-dihydronapthalene (1,2-dihydronapthalene oxide).

1,2-Dihydronapthalene Oxide

1,2-dihydronapthalene oxide has two chiral centres at each epoxy carbon, as shown in the following figure.

The two chiral centres associated with the epoxide must exist as (R,S) or (S,R) due to the syn-substitution of the epoxy oxygen across the alkene double bond, and thus the two chiral centres can be treated as one chiral centre. One conformational chiral plane arises from the geometry of the C9-C10 bond in the hexane ring, which can either slope up or down with respect to the benzene ring plane. The epoxy chiral centres gives rise to 2² (four) enantiomers, two of which cannot exist favourably due to the syn-oxygen substitution. For each of the two allowed enantiomers, (R,S) and (S,R), two chiral conformations can exist. The chiral conformers can interconvert into each other through chair-antichair inversions of the cyclohexane ring. These are described in the figure below.

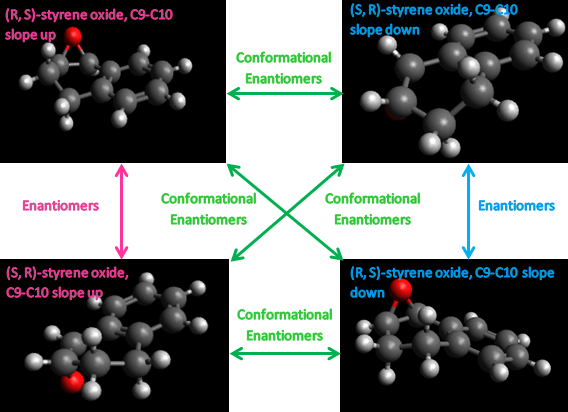
The two enantiomers of of 1,2-dihydronapthalene oxide and their conformational isomers

Each of the configurational and conformational isomers was modelled in Avogadro to the MMFF94s, conjugate gradient level of theory. Initial structures were minimised to obtain a minimum energy geometry for each isomer. These are as tabulated below.

Isomer	Conformer 1		Conformer 2		Conformer 3
Isomer	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)
(S,R)-1,2-dihydronapthalene oxide (C9-C10 slope up)	1,2-dihydronapthalene oxide 30.68348 kcal/mol	Total Electronic Energy = 5.07558 Total Van der Waals = 19.97117 Total Out-of-Plane Bending Energy = 0.02988 Total Torsional Energy = 1.01016 Total Stretch Bending Energy = -0.80380 Total Angle Bending Energy = 2.61823 Total Bond Stetching Energy = 2.78225 Total Energy = 30.68348	1,2-dihydronapthalene oxide 30.68347 kcal/mol	Total Electronic Energy = 5.07650 Total Van der Waals = 19.95799 Total Out-of-Plane Bending Energy = 0.03054 Total Torsional Energy = 1.01520 Total Stretch Bending Energy = -0.80232 Total Angle Bending Energy = 2.62588 Total Bond Stetching Energy = 2.77968 Total Energy = 30.68347	1,2-dihydronapthalene oxide 30.68364 kcal/mol	Total Electronic Energy = 5.07403 Total Van der Waals = 19.97645 Total Out-of-Plane Bending Energy = 0.02967 Total Torsional Energy = 1.01202 Total Stretch Bending Energy = -0.80469 Total Angle Bending Energy = 2.61375 Total Bond Stetching Energy = 2.78242 Total Energy = 30.68364
(S,R)-1,2-dihdronapthalene oxide (C9-C10 slope down)	1,2-dihydronapthalene oxide 30.22445 kcal/mol	Total Electronic Energy = 5.15408 Total Van der Waals = 19.38146 Total Out-of-Plane Bending Energy = 0.00922 Total Torsional Energy = 1.67327 Total Stretch Bending Energy = -0.86999 Total Angle Bending Energy = 2.17888 Total Bond Stretching Energy = 2.69754 Total Energy = 30.22445	1,2-dihydronapthalene oxide 30.22440 kcal/mol	Total Electronic Energy = 5.15300 Total Van der Waals = 19.37922 Total Out-of-Plane Bending Energy = 0.00939 Total Torsional Energy = 1.67403 Total Stretch Bending Energy = -0.86951 Total Angle Bending Energy = 2.18029 Total Bond Stretching Energy = 2.69798 Total Energy = 30.22440
(R,S)-1,2-dihydronapthalene oxide (C9-C10 slope down)	1,2-dihydronapthalene oxide 30.68345 kcal/mol ‎	Total Electronic Energy = 5.07563 Total Van der Waals = 19.96768 = Total Out-of-Plane Bending Energy = 0.03003 Total Torsional Energy = 1.01200 Total Stretch Bending Energy = -0.80345 Total Angle Bending Energy = 2.61984 Total Bond Stretching Energy = 2.78171 Total Energy = 30.68345	1,2-dihydronapthalene oxide 30.68344 kcal/mol ‎	Total Electronic Energy = 5.07608 Total Van der Waals = 19.96371 Total Out-of-Plane Bending Energy = 0.03025 Total Torsional Energy = 1.01298 Total Stretch Bending Energy = -0.80303 Total Angle Bending Energy = 2.62238 Total Bond Stretching Energy = 2.78106 Total Energy = 30.68344
(S,R)-1,2-dihydronapthalene oxide (C9-C10 slope up)	1,2-dihydronapthalene oxide 30.22442 kcal/mol	Total Electronic Energy = 5.15329 Total Van der Waals = 19.37677 Total Out-of-Plane Bending Energy = 0.00950 Total Torsional Energy = 1.67492 Total Stretch Bending Energy = -0.86888 Total Angle Bending Energy = 2.18145 Total Bond Stretching Energy = 2.69737 Total Energy = 30.22442	1,2-dihydronapthalene oxide 30.22441 kcal/mol‎	Total Electronic Energy = 5.15317 Total Van der Waals = 19.37800 Total Out-of-Plane Bending Energy = 0.00944 Total Torsional Energy = 1.67446 Total Stretch Bending Energy = -0.86923 Total Angle Bending Energy = 2.18084 Total Bond Stretching Energy = 2.69775 Total Energy = 30.22441

As expected, the conformational isomers, (S,R)-1,2-dihydronapthalene oxide (C9-C10 slope up) and (S,R)-1,2-dihydronapthalene oxide (C9-C10 slope down), and (R,S)-1,2-dihydronapthalene oxide (C9-C10 slope up) and (R,S)-1,2-dihydronapthalene oxide (C9-C10 slope down),give the same energy to within 0.00001 kcal/mol, whilst of the two (S,R) and (R,S)-1,2-dihydronapthalene oxide enantiomers,the (S,R) enantiomer gives a lower energy, and thus is predicted to be more stable than the (R,S) configuration.

NMR

Calculation of Oxide Correction Constants

To allow for the correction factors of the epoxy carbons, ethane and ethylene oxide were modelled using the MMFF94s force field with conjugate gradients in Avogadro. These input structures were optimised to DFT B3LYP level of theory using the 6-31G(d,p) basis set, and NMR calculations carried out on the optimised structures.

Ethane

The MMFF94s optimised structure used as input to the DFT B3LYP level of theory optimisation is shown below.

Ethane geometry optimised using MMFF94s force field‎

‎

Ethane

Energy parameters associated with this structure are as tabulated.

Energy Contribution	Energy (kcal/mol)
Total Electrostatic Energy	0.00000
Total Van der Waals Energy	0.11175
Total Out-of-Plane Bending Energy	0.00000
Total Stretch Bending Energy	-0.00153
Total Torsional Energy	-4.95900
Total Angle Bending Energy	0.01595
Total Bond Stretching Energy	0.00742
Total Energy	-4.82541

Ethylene oxide

Ethylene oxide was modelled using the MMFF94s force field in Avogadro, optimised to the DFT B3LYP 6-31G(d,p) level of theory with an NMR simulation carried out. The structure used as DFT B3LYP optimisation input is demonstrated below.

Ethylene oxide geometry optimised using MMFF94s force field‎

Ethylene oxide

Energy parameters associated with this structure are tabulated below.

Energy Contribution	Energy (kcal/mol)
Total Electrostatic Energy	3.49639
Total Van der Waals Energy	0.01963
Total Out-of-Plane Bending Energy	0.00000
Total Stretch Bending Energy	-0.00982
Total Torsional Energy	2.35781
Total Angle Bending Energy	0.18271
Total Bond Stretching Energy	0.00462
Total Energy	6.05133

Correction Factors

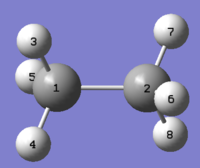
The ethane and ethylene structures gave ¹³C NMR peaks corrected with reference: TMS B3LYP/6-31G(d,p) Chloroform of shielding 192.17 ppm with NMR Degeneracy Tolerance of 0.05. Numbering used when referring to ethane atom shifts are made with refernce to the figure below.

The calculated C-O oxide δcorr (ppm) was given by subtracting the ethylene shift from the ethane shift for the equivalent atoms and are as documented in the table below.

Ethane 6-31G(d,p)				Ethylene 6-31G(d,p)
Carbon Number	δcalc (ppm)	Average δcalc (ppm)	Carbon Number	δcalc (ppm)	Average δcalc (ppm)	δcorr (ppm)
C1	9.4675	9.4675	C1	41.194	41.19395	31.72645
C2	9.4675		C2	41.1939

The equivalent analysis for ¹H NMR spectra corrected with reference: TMS B3LYP/6-31G(d,p) Chloroform of shielding reference 31.7462 ppm and NMR Degeneracy Tolerance of 0.05

Ethane 6-31G(d,p)				Ethylene 6-31G(d,p)
Hydrogen Number	δcalc (ppm)	Average δcalc (ppm)	Hydrogen Number	δcalc (ppm)	Average δcalc (ppm)	δcorr (ppm)
H4	0.9506	0.949933333	H1	2.6096	2.6096	1.659666667
H7	0.9504		H2	2.6096
H5	0.9504		H3	2.6096
H3	0.9488		H4	2.6096
H6	0.9488
H8	0.9504

It is well reported that the ¹H NMR spectrum of ethane has one signal which is an average of all hydrogen signals in the rapidly interchanging conformations adopted by ethane in solution occurring by rotation around the central C-C bond. ^[23] However the presently calculated spectrum exhibits three different signals, one for each equivalent hydrogen pair in ethane. This reinforces the static nature of the simulation, which takes into account only the one conformation. In this case, this conformer is the lowest energy staggered conformation, which provides the most accurate representation of the molecule as this conformer, residing at an energy minimum, is the dominant conformation found for a selection of ethane molecules at any given time. The six signals were averaged to give one signal. This provides a rather poor representation of the conformations in solution however, as the experimental final shift is an average of those observed for each conformation. The δcorr (ppm) was given by subtracting the ethylene shift from the ethane shift.

1,2-dihydronapthalene oxide NMR

The NMR simulation was carried out on the lowest energy conformer as this structure represents the dominant structure at any one time in solution. Referring to the table above, this gives the 30.22440 kcal/mol isomer.

Higher Level of Theory

The NMR was also carried out using the DFT B3LYP cc-pVTZ level of theory.This gave a structure with thermal free energies of:

Sum of electronic and thermal Energies= -462.280088
Sum of electronic and thermal Enthalpies= -462.279
Sum of electronic and thermal Free Energies= -462.320756

The ¹³C NMR and ¹H NMR spectra were corrected for TMS B3LYP/cc-pVTZ GIAO are as shown below, respectively.

These results were compared with literature for the (+)-enantiomer, ^[24] and disparity with experimental shifts calculated and tabulated below.

Carbon Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
C1	26.3666	22.2		4.1666	5.14473	8.1021	4.1666	-0.30897	-23.77355
C2	60.3019	55.5	31.72645	4.8019			-23.77355
C3	57.688	55.2	31.72645	2.488			-23.47355
C4	141.0021	132.9		8.1021			8.1021
C5	145.0906	137.1		7.9906			7.9906
C6	29.297	24.8		4.497			4.497
C7	133.4602	128.8		4.6602			4.6602
C8	133.5733	128.8		4.7733			4.7733
C9	131.242	126.5		4.742			4.742
C10	135.1256	129.9		5.2256			5.2256

The carbon NMR spectrum was compared with literature for the (-)-enantiomer, ^[25] giving results tabulated below.

Carbon Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
C1	26.3666	20.8		5.5666	6.77473	9.5021	5.5666	1.32103	-22.37355
C2	60.3019	54.1	31.72645	6.2019			-22.37355
C3	57.688	51.7	31.72645	5.988			-19.97355
C4	141.0021	131.5		9.5021			9.5021
C5	145.0906	135.6		9.4906			9.4906
C6	29.297	23.4		5.897			5.897
C7	133.4602	127.3		6.1602			6.1602
C8	133.5733	127.4		6.1733			6.1733
C9	131.242	125.1		6.142			6.142
C10	135.1256	128.5		6.6256			6.6256

The calculated carbon shifts have a 1.63 ppm larger disparity with the (-)-enantiomer ^[25] than with the (+)-enantiomer ^[24] literature carbon shifts. The disparity between literature shifts and the calculated shifts is due to the static nature of the molecule being run in the calculation, which is of one configuration and conformation. In reality the molecule is dynamic, and making transitions between different energetically available conformers on the submillisecond timescale, and so the different proton shifts that occur in each conformer are completely averaged out on the NMR timescale, which is ~1 sec. Thus a spectrum that is an average of the exchanging states is yielded. The interconversion between conformers is fast on the NMR time scale as it occurs at a much greater rate than the frequency difference between the two conformers. The difference in frequency depends on the Larmor frequency of the observed nucleus and the magnetic field strength, thus changing the magnetic field strength and cooling the solution undergoing the NMR experimental analysis would allow recreation of the static calculated spectrum of one conformer which lies at the energy minimum.
Additionally, intermolecular coupling between molecules is not taken account of in the calculated spectrum, which considers only one molecule. Thus coupling constants and peak multiplicity in the observed spectra would be expected to differ with those present in the calculated spectra.

The equivalent analysis was undertaken for the ₁H NMR spectrum. Below is documented the calculated _{1_{H NMR shifts calcualted at the DFT B3LYP cc-pVTZ level of theory and their disparity with literature shifts for the (+)-enantiomer}}

Hydrogen Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
H11	7.4035	7.018		0.3855	0.281076667	0.8442	0.3855	-0.13544	-2.122333333
H12	7.5534	7.1754		0.378			0.378
H13	7.5182	7.1356		0.3826			0.3826
H14	7.7166	7.322		0.3946			0.3946
H15	2.5507	2.2555		0.2952			0.2952
H16	2.8556	2.715666667		0.139933333			0.139933333
H17	2.3642	1.52		0.8442			0.8442
H18	1.6547	1.6988		-0.0441			-0.0441
H20	3.6844	3.667666667	1.659666667	0.016733333			-2.008
H21	3.8001	3.782	1.659666667	0.0181			-2.122333333

Th _{1_{H NMR shift were compared with literature for the (-)-enantiomer.^[25] Results are as tabulated below.}}

Hydrogen Number	δcalc (ppm)	Average δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
H11	7.4035		7.01		0.3935	0.19252	0.0142	0.3935	-0.223996667	-2.120333333
H12	7.5534	7.5358	7.1356		0.4178			0.4178
H13	7.5182	7.5358	7.1356		0.3826			0.3826
H14	7.7166		7.34		0.3766			0.3766
H15	2.5507		2.45		0.1007			0.1007
H16	2.8556		2.675		0.1806			0.1806
H17	2.3642		2.35		0.0142			0.0142
H18	1.6547		1.65		0.0047			0.0047
H20	3.6844		3.65	1.659666667	0.0344			-1.990333333
H21	3.8001		3.78	1.659666667	0.0201			-2.120333333

A Higher Energy Enantiomer, 30.22441 kcal/mol input energy

To allow for a comparison of the lowest energy isomer NMR, an additional NMR of a higher entropy isomer was carried out on (S,R)-1,2-dihydronapthalene oxide, of input energy 30.22441 kcal/mol, modelled at the DFT B3LYP 6-31G(d,p) level of theory in chloroform solvent, giving the structure shown below.

Numbering used for the ¹H NMR and ¹³C NMR spectra of 1,2-dihydronapthalene oxide 30.22441 kcal/mol at DFT B3LYP 6-31G(d,p)level of theory

Electron density surface of 1,2-dihydronapthalene oxide 30.22441 kcal/mol at DFT B3LYP 6-31G(d,p)level of theory, coloured by electrostatic potential

HOMO of 1,2-dihydronapthalene oxide 30.22441 kcal/mol at DFT B3LYP 6-31G(d,p)level of theory, coloured by electrostatic potential

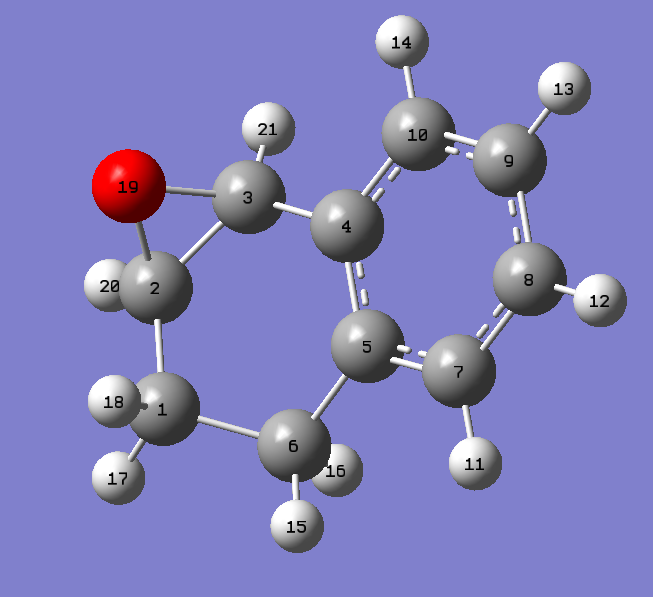
Following TMS/DFT B3LYP 6-31G(d,p) (chloroform) correction application, this gave ¹H and ¹³C NMR spectra as documented below.

¹H NMR data

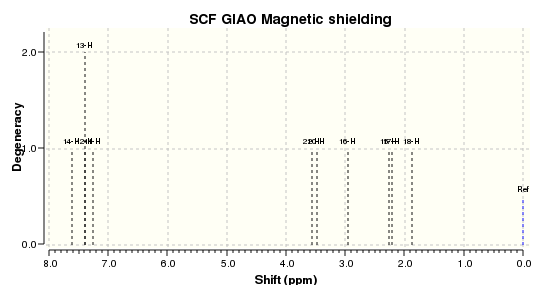
Comparison of B3LYP 6-31G(d,p) optimised structure with MMFF94s force field, conjugate gradient optimisation algorithm

The 30.2441 kcal/mol (S,R)-1,2-dihydronapthalene oxide conformer was optimised through the HPC using Gaussian 09 to the DFT B3LYP 6-31G (d,p) level of theory, and NMR, IR and VCD simulations run on this optimised configuration. Energetics of the optimised molecule are reported in the table below. The lower total energy of the molecule when run to the DFT B3LYP level of theory is lower than at the MMFF94s, conjugate gradient level of theory.

Energy Contribution	Energy (kcal/mol)
Total Electrostatic Energy	-4.01005
Total Van der Waals Energy	18.10016
Total Out-of-Plane Bending Energy	0.01243
Total Stretch Bending Energy	-0.46660
Total Torsional Energy	1.92867
Total Angle Bending Energy	3.35949
Total Bond Stretching Energy	3.11745
Total Energy	22.04156

Comparison of ¹H NMR data with (+)-1,2-Dihydronapthalene Oxide Literature

Comparing the calculated NMR shifts with D. Xiong et al. (USE REFERENCE IN FIGURE), the disparity between calculated and experimental shifts could be found. This is reported in the following table and figure.

Hydrogen Number	δcalc (ppm)	δexp (ppm)	∆δ (ppm)
H11	7.251492731	7.01	0.241492731
H12	7.391151507	7.18	0.211151507
H13	7.387571667	7.185	0.202571667
H14	7.615118252	7.34	0.275118252
H15	2.267285883	2.45	-0.182714117
H16	2.946631263	2.675	0.271631263
H17	2.209025512	2.35	-0.140974488
H18	1.873442614	1.65	0.223442614
H20	3.483067617	3.65	-0.166932383
H21	3.559560436	3.78	-0.220439564

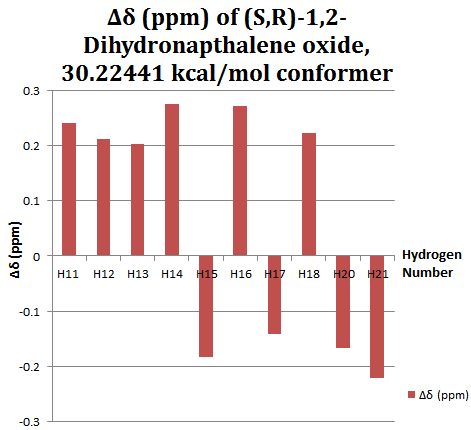
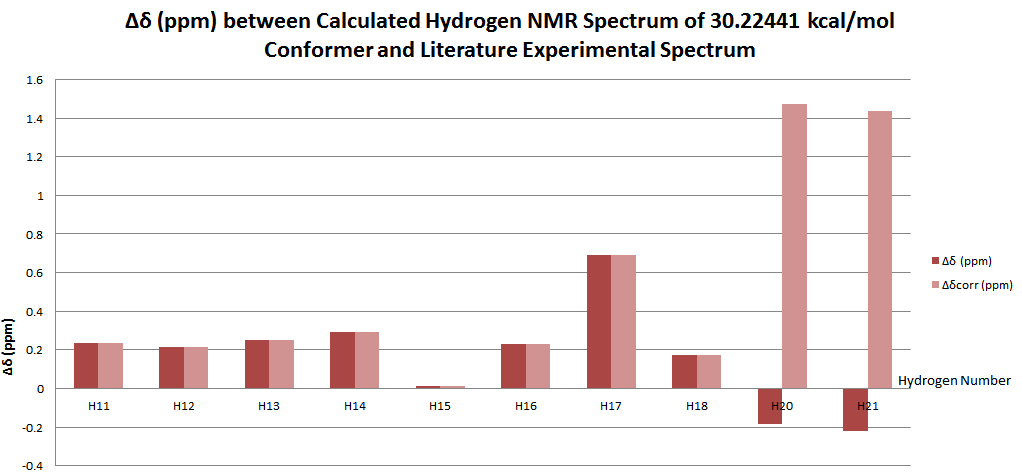
^{1</>H NMR ∆δ (ppm) of (S,R)-1,2-Dihydronapthalene oxide, 30.22441 kcal/mol conformer with literature D. Xiong, X. Hu, S. Wang, C.-X. Miao, C. Xia, W. Sun,E. J. Org. Chem., 2011, 2011, 23, 4289–4292}

^{1</>H NMR ∆δ (ppm) of (-)-1,2-Dihydronapthalene oxide 30.22441 kcal/mol}

Carbon NMR Comparison with (-)-Rotamer

Carbon Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
C1	29.06348904	20.8		8.263489036	0.03509053	8.263489036	8.263489036	-4.120980016	-22.37355
C2	52.82116189	54.1	31.72645	-1.278838112			-22.37355
C3	52.19244356	51.7	31.72645	0.492443564			-19.97355
C4	130.3705995	131.5		-1.129400532			-1.129400532
C5	135.38776	135.6		-0.212240025			-0.212240025
C6	30.18028122	23.4		6.780281225			6.780281225
C7	123.533413	127.3		-3.76658704			-3.76658704
C8	123.7910881	127.4		-3.60891185			-3.60891185
C9	121.7441924	125.1		-3.355807577			-3.355807577
C10	126.6664766	128.5		-1.833523393			-1.833523393

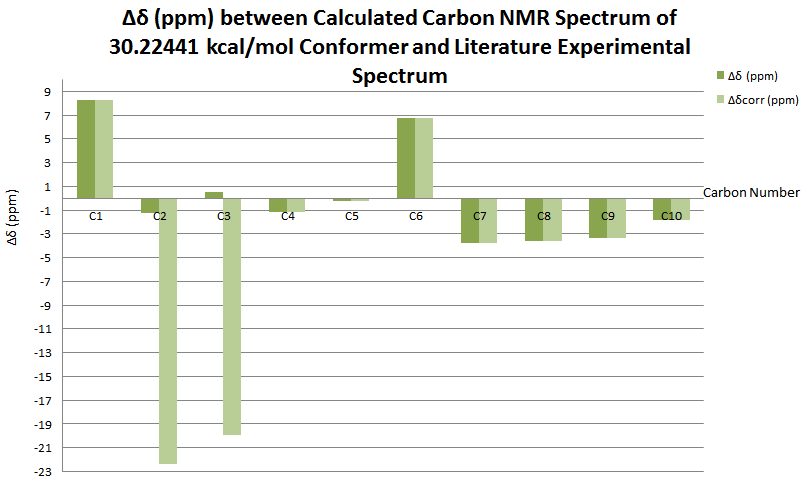
(-)-1,2-Dihydronapthalene oxide Literature Comparison

Further literature comparison with the (-)-rotamer was undertaken as a comparative study with the (+)-rotamer.

¹³C NMR data=

At the B3LYP 6-31G level of theory, ¹³C NMR spectrum is as below.

The Carbon shifts and disparity with literature^[26] is as noted below.

Carbon Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
C1	29.06348904	20.8		8.263489036	0.03509053	8.263489036	8.263489036	-4.120980016	-22.37355
C2	52.82116189	54.1	31.72645	-1.278838112			-22.37355
C3	52.19244356	51.7	31.72645	0.492443564			-19.97355
C4	130.3705995	131.5		-1.129400532			-1.129400532
C5	135.38776	135.6		-0.212240025			-0.212240025
C6	30.18028122	23.4		6.780281225			6.780281225
C7	123.533413	127.3		-3.76658704			-3.76658704
C8	123.7910881	127.4		-3.60891185			-3.60891185
C9	121.7441924	125.1		-3.355807577			-3.355807577
C10	126.6664766	128.5		-1.833523393			-1.833523393

The literature disparity is summarised in the following table.

Comparison of ¹³C NMR data with Literature

Repeat of NMR Analysis Using a Different Conformer and Higher Level of Theory

The MMFF94s force field, conjugate gradient algorithm optimised structures of the 30.2244 kcal/mol configurational isomer and the 30.6834 kcal/mol isomer were optimised further using Gaussian09 at the DFT B3LYP 6-31G(d,p) level of theory. These structures were input into optimisation at the higher DFT B3LYP cc-pVTZ level of theory, and NMR simulations carried out on both optimised structures. Results are as documented below.

30.68344 kcal/mol isomer at the 6-31G (d,p) level of theory

The ¹³C NMR spectrum of this isomer was corrected with reference TMS B3LYP/6-31G(d,p) Chloroform and reference shielding 192.17 ppm and NMR Degeneracy Tolerance of 0.05.

Atomic numbering used for the 30.68344 kcal/mol isomer is shown below.

The ¹³C NMR spectrum is shown below, with corrected shifts and comparison with literature,^[26] tabulated.

Carbon Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
C1	24.94531918	20.8		4.145319183	-0.267577089	-4.145319183	4.145319183	6.077712911	34.85481801
C2	56.4348396	54.1	88.1612896	2.334839596			34.0612896
C3	54.82836801	51.7	86.55481801	3.128368014			34.85481801
C4	130.383024	131.5		-1.116975979			-1.116975979
C5	133.8418328	135.6		-1.758167178			-1.758167178
C6	28.03616498	23.4		4.63616498			4.63616498
C7	123.8353838	127.3		-3.464616185			-3.464616185
C8	123.425036	127.4		-3.974963965			-3.974963965
C9	121.4413171	125.1		-3.658682863			-3.658682863
C10	125.5529435	128.5		-2.947056492			-2.947056492

Applying the oxide C-O correction in fact increases the disparity with literature,^[26] as can be seen in the following figure.

This may be due to the poor modelling of the simple ethylene oxide environment used for carbon correction factors when compared to the increased complexity of benzylic environment present for 1,2-dihydronapthalene. TALK ABOUT NAPTHALENE HERE!!!!

The equivalent analysis was carried out for the ¹H NMR spectrum, and is documented below.

X-Axis: Shift (ppm)

Y-Axis: Degeneracy
Reference: TMS B3LYP/6-31G(d,p) Chloroform
Reference shielding: 31.7462 ppm
NMR Degeneracy Tolerance: 0.05
X Y Degeneracy

14-H 7.4903000000 1.0000000000 1.0000000000 12-H 7.4035000000 1.0000000000 2.0000000000 13-H 7.3689000000 2.0000000000 2.0000000000 11-H 7.1952000000 1.0000000000 1.0000000000 21-H 3.6098000000 1.0000000000 2.0000000000 20-H 3.5657000000 2.0000000000 2.0000000000 16-H 2.8801000000 1.0000000000 1.0000000000 15-H 2.2677000000 1.0000000000 1.0000000000 18-H 2.2162000000 1.0000000000 1.0000000000 17-H 1.5628000000 1.0000000000 1.0000000000

To allow for comparison with literature, ^[27] the original spectra were used to refer to peaks notated as a "multiplet" in literature, and the peaks corresponding to one hydrogen environment were identified. For those hydrogens which observed coupling, each peak present in the multiplet was identified and these peaks averaged to find the centre of the multiplet, which corresponds to the chemical shift of the hydrogen.

Hydrogen Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
H11	7.1952	7.018		0.1772	0.126956667	6.8408	0.1772	0.45889	-0.050243333
H12	7.4035	7.1754		0.2281			0.2281
H13	7.3689	7.1356		0.2333			0.2333
H14	7.4903	7.322		0.1683			0.1683
H15	2.2677	2.2555		0.0122			0.0122
H16	2.8801	2.715666667		0.164433333			0.164433333
H17	1.5628	1.52		0.0428			0.0428
H18	2.2162	1.6988		0.5174			0.5174
H20	3.5657	3.667666667	5.225366667	-0.101966667			1.5577
H21	3.6098	3.782	5.269466667	-0.1722			1.487466667

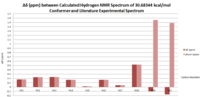
As for the carbon spectrum, applying the oxide hydrogen correction in fact increases the disparity between calculated results and literature, albeit the increase between these results is much lower, ~1.6 ppm for the hydrogen c.f ~32 ppm for the carbon NMR spectrum. This is most probably due to the increase distance between the hydrogens and epoxide oxygen, which gives the smaller correction factor calculated in the ethane model. Nevertheless, the increase in disparity reinforces the conclusion that the ethane environment is too oversimplified to allow for accurate correction factors. In general, the difference between the calculated and literature ¹H NMR peaks^[27] is lower than that observed for the ¹³C NMR spectrum.

30.68344 kcal/mol isomerAt the cc-pVTZ level of theory

H nmr spec napth oxide cc-pvtz 30.68344.PNG

Reference: TMS B3LYP/6-31G(d,p) Chloroform Reference shielding: 31.7462 ppm NMR Degeneracy Tolerance: 0.05

14-H 7.7291000000 1.0000000000 1.0000000000 12-H 7.5659000000 1.0000000000 2.0000000000 13-H 7.5307000000 2.0000000000 2.0000000000 11-H 7.4160000000 1.0000000000 1.0000000000 21-H 3.8126000000 1.0000000000 1.0000000000 20-H 3.6970000000 1.0000000000 1.0000000000 16-H 2.8681000000 1.0000000000 1.0000000000 15-H 2.5632000000 1.0000000000 1.0000000000 18-H 2.3767000000 1.0000000000 1.0000000000 17-H 1.6672000000 1.0000000000 1.0000000000

C nmr spec napth oxide cc-pvtz 30.68344.PNG X-Axis: Shift (ppm)

Y-Axis: Degeneracy
Reference: TMS B3LYP/6-31G(d,p) Chloroform
Reference shielding: 192.17 ppm
NMR Degeneracy Tolerance: 0.05
X Y Degeneracy

5-C      152.8919000000        1.0000000000        1.0000000000
4-C      148.8033000000        1.0000000000        1.0000000000

10-C 142.9270000000 1.0000000000 1.0000000000

8-C      141.3746000000        1.0000000000        1.0000000000
7-C      141.2615000000        1.0000000000        1.0000000000
9-C      139.0433000000        1.0000000000        1.0000000000
2-C       68.1034000000        1.0000000000        1.0000000000
3-C       65.4894000000        1.0000000000        1.0000000000
6-C       37.0983000000        1.0000000000        1.0000000000
1-C       34.1679000000        1.0000000000        1.0000000000

30.22440 kcal/mol isomer

C nmr spec napth oxide cc-pvtz 30.2244.PNG

X-Axis:  Shift (ppm)

Y-Axis: Degeneracy
Reference: TMS B3LYP/6-31G(d,p) Chloroform
Reference shielding: 192.17 ppm
NMR Degeneracy Tolerance: 0.05
X Y Degeneracy

5-C      152.8919000000        1.0000000000        1.0000000000
4-C      148.8034000000        1.0000000000        1.0000000000

10-C 142.9269000000 1.0000000000 1.0000000000

8-C      141.3746000000        1.0000000000        1.0000000000
7-C      141.2615000000        1.0000000000        1.0000000000
9-C      139.0433000000        1.0000000000        1.0000000000
2-C       68.1032000000        1.0000000000        1.0000000000
3-C       65.4893000000        1.0000000000        1.0000000000
6-C       37.0983000000        1.0000000000        1.0000000000
1-C       34.1679000000        1.0000000000        1.0000000000

H nmr spec napth oxide cc-pvtz 30.2244.PNG

X-Axis: Shift (ppm)

Y-Axis: Degeneracy
Reference: TMS B3LYP/6-31G(d,p) Chloroform
Reference shielding: 31.7462 ppm
NMR Degeneracy Tolerance: 0.05
X Y Degeneracy

14-H 7.7291000000 1.0000000000 1.0000000000 12-H 7.5659000000 1.0000000000 2.0000000000 13-H 7.5307000000 2.0000000000 2.0000000000 11-H 7.4160000000 1.0000000000 1.0000000000 21-H 3.8126000000 1.0000000000 1.0000000000 20-H 3.6969000000 1.0000000000 1.0000000000 16-H 2.8681000000 1.0000000000 1.0000000000 15-H 2.5632000000 1.0000000000 1.0000000000 17-H 2.3767000000 1.0000000000 1.0000000000 18-H 1.6672000000 1.0000000000 1.0000000000

IR and VCD analysis

IR and VCD analysis was carried out for the lowest energy isomer at input 30.2244 kcal/mol, optimised to the DFT B3LYP cc-pVTZ level of theory, with results as below.

Napth ox 30.2244 IR cc-pVTZ im.PNG

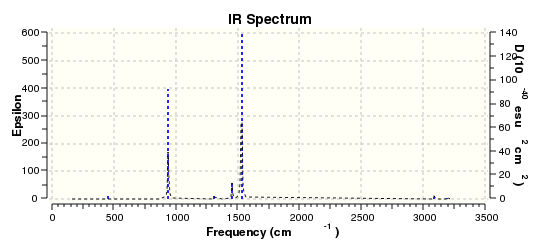
VCD can be used to elucidate the enantioeric excess (ee) of a sample consisting of a mixture of enantiomers of a chiral molecule. The sample % ee is defined as:

(N_A - N_B) x 100%/ (N_A + N_B)

where N_A and N_A is a measure of moles of enantiomer A and enantiomer B respectively. ^[28]This expression is equivalent to the excess amount of one enantiomer over the other relative to the total amount of both enantiomers. Optically pure samples of A have 100% ee, racemic mixtures 0% and optically pure B sample have -100% purity. VCD can be used for ee determination from the multiplicity of spectral bands that can be measure simultaneously in one spectrum. The intensity of the VCD bands gives an indication of the ee, as each VCD spectrum for each enantiomer is a mirror image of the other. ^[29]

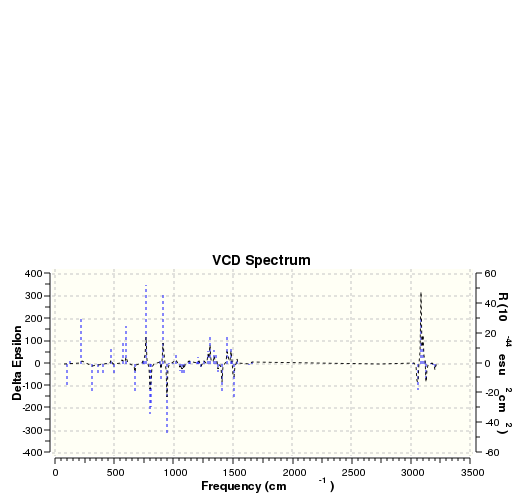
Styrene oxide Configurations

Styrene oxide has a chiral center at the benzylic carbon atom, giving (R)-styrene oxide and (S)-styrene oxide enantiomers. The energies of these two enantiomers were minimised to the MMFF94s, conjugate gradient level of theory.

Enantiomer	Conformer 1		Conformer 2		Conformer 3
Enantiomer	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)	Structure	Energy Contribution (kcal/mol)
R-styrene oxide	R-styrene oxide 21.61506 kcal/mol	Total Electronic Energy = 3.07365 Total Van der Waals = 13.67376 Total Out-of-Plane Bending Energy = 0.00164 Total Torsional Energy = 2.34616 Total Stretch Bending Energy = -0.74666 Total Angle Bending Energy = 1.42461 Total Bond Stetching Energy = 1.84188 Total Energy = 21.61506	R-styrene oxide 21.61547 kcal/mol	Total Electronic Energy = 3.08594 Total Van der Waals = 21.61547 Total Out-of-Plane Bending Energy = 0.00169 Total Torsional Energy = 2.34606 Total Stretch Bending Energy = -0.74594 Total Angle Bending Energy = 1.42450 Total Bond Stetching Energy = 1.84036 Total Energy = 30.68347
S-styrene oxide	S-styrene oxide 21.61503 kcal/mol	Total Electronic Energy = 3.07620 Total Van der Waals = 13.67135 Total Out-of-Plane Bending Energy = 0.00166 Total Torsional Energy = 2.34617 Total Stretch Bending Energy = -0.74656 Total Angle Bending Energy = 1.42457 Total Bond Stretching Energy = 1.84164 Total Energy = 21.61503	S-styrene oxide 21.61507 kcal/mol	Total Electronic Energy = 3.07301 Total Van der Waals = 13.67434 Total Out-of-Plane Bending Energy = 0.00164 Total Torsional Energy = 2.34620 Total Stretch Bending Energy = -0.74667 Total Angle Bending Energy = 1.42456 Total Bond Stretching Energy = 1.84199 Total Energy = 21.61507	S-styrene oxide 21.61508 kcal/mol	Total Electronic Energy = 3.07293 Total Van der Waals = 13.67443 Total Out-of-Plane Bending Energy = 0.00164 Total Torsional Energy = 2.34616 Total Stretch Bending Energy = -0.74669 Total Angle Bending Energy = 1.42463 Total Bond Stretching Energy = 1.84199 Total Energy = 21.61508

NMR analysis of S-styrene oxide

The NMR of (S)-styrene oxide was modelled at the DFT B3LYP 6-31G(d,p) level of theory in chloroform solvent, giving the structure as shown below.

(S)-styrene oxide at DFT B3LYP 6-31G(d,p)level of theory‎

Following TMS/DFT B3LYP 6-31G(d,p) (chloroform) correction application, this gave ¹H and ¹³C NMR spectra as documented in the figures below.

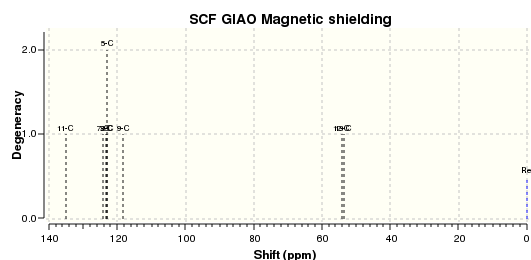
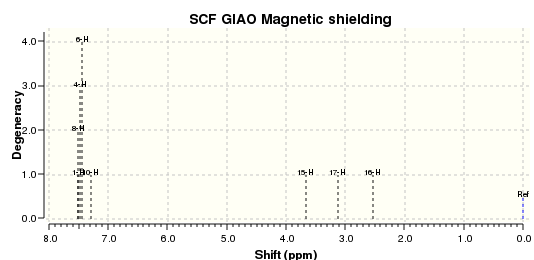
Numbering of atoms used in the following NMR analysis is demonstrated below.

Comparison of S-styrene Oxide with Literature

The carbon shifts were compared with both S-styrene oxide NMR and R-styrene oxide literature NMR shifts.

Comparison with R-styrene oxide literature shifts (K. Sarma, N. Bhati et al.) is as documented below.

Carbon Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
C2	122.9659755	128.1		-5.134024522	-7.231939222	5.134024522	11.7736977	33.982242
C3	123.4152252	128.5		-5.0847748		5.0847748
C5	122.9534464	125.5		-2.546553554		2.546553554
C7	124.1326453	128.5		-4.367354719		4.367354719
C9	118.2680608	125.5		-7.231939222		7.231939222
C11	135.1343367	137.6		-2.465663325		2.465663325
C12	54.05057945	52.4	85.77702945	1.650579448		33.37702945
C13	53.455792	51.2	85.182242	2.255791999		33.982242

Comparison with S-styrene oxide NMR literature was carried out,(Synthesis 2011(7): 1092-1098) with results as follows:

¹³C NMR

Carbon Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
C2	122.9659755	128.1		-5.134024522	-2.865492337	-7.231939222	5.134024522	11.7736977	33.982242
C3	123.4152252	128.5		-5.0847748			5.0847748
C5	122.9534464	125.5		-2.546553554			2.546553554
C7	124.1326453	128.5		-4.367354719			4.367354719
C9	118.2680608	125.5		-7.231939222			7.231939222
C11	135.1343367	137.6		-2.465663325			2.465663325
C12	54.05057945	52.4	85.77702945	1.650579448			33.37702945
C13	53.455792	51.2	85.182242	2.255791999			33.982242

Theoretically, no difference should be observed between the experimental NMR of the R- and S- enantiomers. However, comparing the carbon NMR shifts obtained through B3LYP 6-311G(d,p) optimisation and simulation, the shift differences of the carbon NMR spectra with literature reveal that a closer fit is obtained with the literature S-styrene oxide NMR. (Synthesis) The disparity shown between the calculated and experimental shifts is indicative of the conformational transitions and intermolecular coupling ^[1] in solution that are not modelled computationally.

¹H NMR

The hydrogen shifts were compared with literature experimental spectra. The S-isomer literature spectrum ^[30] when compared to the calculate R-isomer spectrum gave parameters as shown.

Hydrogen Number	δcalc (ppm)	Multiplet δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
H1	7.514585625	7.451002894	7.28		0.171002894	-0.069801232	-0.251973718	0.171002894	1.174948768	1.644740884
H4	7.483516459
H6	7.446452754
H8	7.512661831
H10	7.2977978
H15	3.662441679		3.84575	5.322108346	-0.183308321			1.476358346
H16	2.534026282		2.786	4.193692949	-0.251973718			1.407692949
H17	3.114074217		3.129	4.773740884	-0.014925783			1.644740884

This is summarised in the shift difference graph below.

Comparison with R-styrene oxide literature (K. Sarma, N. Bhati) gave a slightly closer fit of calculated hydrogen shifts to experimental shifts.

Hydrogen Number	δcalc (ppm)	Multiplet δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
H1	7.514585625	7.451002894	7.31		0.141002894	-0.094613732	-0.275973718	0.141002894	1.150136268	1.623740884
H4	7.483516459
H6	7.446452754
H8	7.512661831
H10	7.2977978
H15	3.662441679		3.87	5.322108346	-0.207558321			1.452108346
H16	2.534026282		2.81	4.193692949	-0.275973718			1.383692949
H17	3.114074217		3.15	4.773740884	-0.035925783			1.623740884

The closer fit is summarised in the shift difference graph below.

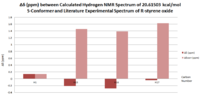
The closer fit of carbon NMR to the S-Styrene oxide literature conflicts with the closer fit of the hydrogen NMR to the R-Styene oxide literature, hinting towards the theoretical equivalence of the R- and S-enantiomer NMR spectra. Further literature would need to be carried out to gain a wider appreciation of such an effect. Additionally, it can be seen that correcting for the oxide hydrogens and carbons in fact increases disparity with literature.

NMR analysis of R-Styrene Oxide Lowest Energy Conformer

The 20.61505 kcal/mol conformer was optimised using the DFT B3LYP 6-31G(d,p) level of theory in Gaussian09 and NMR simulation calculatioins were carried out. This gave NMR spectra as shown below.

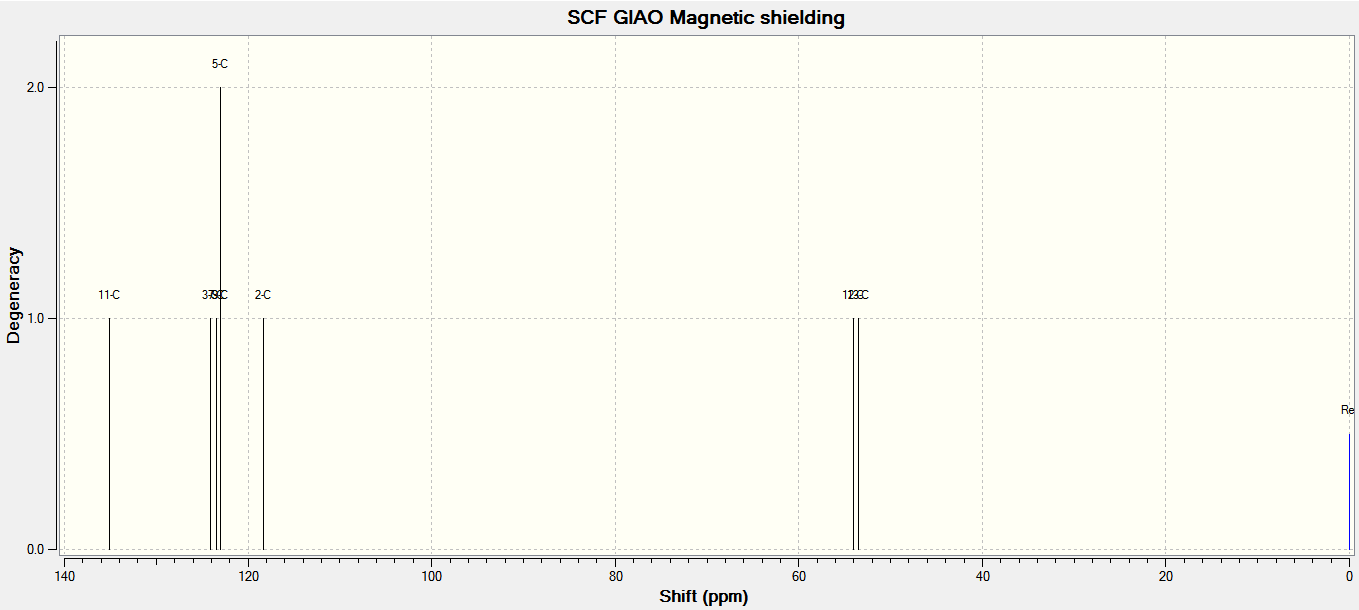
Atomic numbering used when referring to specified atoms in NMR analysis is as shown below.

Numbering of R-styrene oxide used during NMR analysis

Comparison of spectra with (S)-Styrene oxide

Literature NMR spectra of S-Styrene oxide, ^[31] was compared with the calculated NMR spectra. Results for ¹³C NMR spectra are as shown below in the following table and shift difference graph.

Carbon Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
C2	118.2706444	127.7		-9.429355626	-2.463345741	-9.429355626	-9.429355626	1.502460509	2.573722263
C3	124.1340577	128.1		-3.965942316			-3.965942316
C5	122.9525029	125.1		-2.147497079			-2.147497079
C7	123.4136518	128.1		-4.686348199			-4.686348199
C9	122.9586151	125.1		-2.141384907			-2.141384907
C11	135.1341726	137.2		-2.065827374			-2.065827374
C12	54.05586731	51.9	85.78231731	2.155867307			33.88231731
C13	53.47372226	50.9	85.20017226	2.573722263			2.573722263

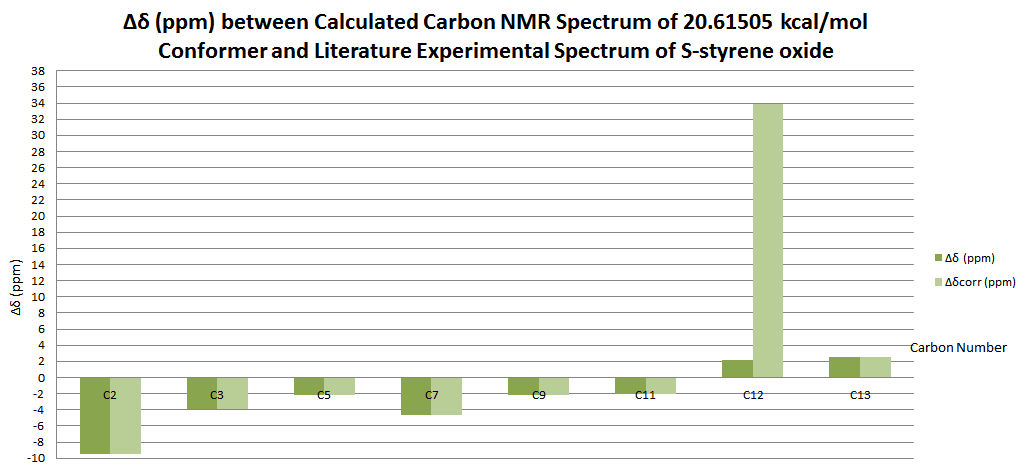
Difference graph of calculated R-styrene oxide ¹C NMR spectra, at DFT B3LYP 6-31G(d,p)level of theory, with experimental literature S-styrene oxide spectrum

Comparison of spectra with (R)-Styrene oxide

Literature NMR spectra of R-Styrene oxide,^[32] was compared with the calculated NMR spectra. Results for ¹³C NMR spectra are as shown below in the following table and shift difference graph.

Carbon Number	δcalc (ppm)	δexp (ppm)	δcorr (ppm)	∆δ (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)	∆δcorr (ppm)	Average ∆δ (ppm)	Mode ∆δ (ppm)
C2	118.2706444	128.1		-9.829355626	-2.863345741	-9.829355626	-9.829355626	5.068266759	34.00017226
C3	124.1340577	128.5		-4.365942316			-4.365942316
C5	122.9525029	125.5		-2.547497079			-2.547497079
C7	123.4136518	128.5		-5.086348199			-5.086348199
C9	122.9586151	125.5		-2.541384907			-2.541384907
C11	135.1341726	137.6		-2.465827374			-2.465827374
C12	54.05586731	52.4	85.78231731	1.655867307			33.38231731
C13	53.47372226	51.2	85.20017226	2.273722263			34.00017226

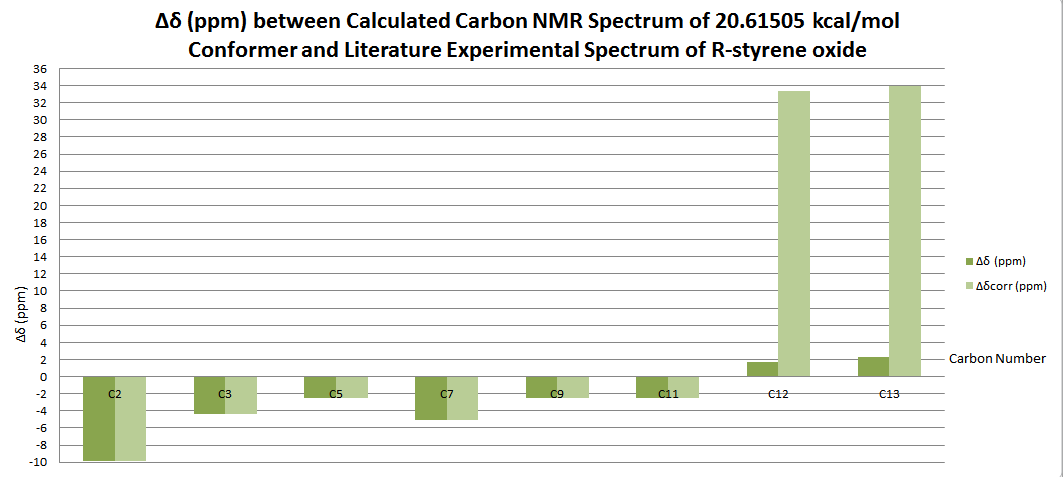
Difference graph of calculated R-styrene oxide ¹C NMR spectra, with experimental literature R-styrene oxide spectrum

IR and VCD analysis of styrene oxide

S-Styrene Oxide

The IR peaks of the lowest energy S-styrene oxide enantiomer, of energy 20.61503 kcal/mol, were compared with literature,^[1] with results tabulated below.

ν (cm^-1	ε_calc	∆ν_calc-exp	Average ∆ν	Mode ∆ν
3031	0.8672364229	-4	0.785714286	12
3038	1.1258300005	3
2975	0.2298337644	0
2919	0	-2
2926	0	5
2933	0.0777506685	12
1603	0.3872326267	-2
1456	2.1668723937	1
1281	5.3363537201	-5
1288	24.6060915808	2
980	2.5214957845	-1
875	6.9168187410	2
763	35.0258886184	3
693	3.9809019461	-3

=R-Styrene Oxide

The IR spectrum for the R-styrene oxide lowest energy isomer was modelled at the DFT B3LYPP 6-31G(d,p) level of theory, and is as shown below.

Through infrared spectroscopy, molecules absorb specific frequencies of non-polarised infrared red that are characteristic of their bonding structure, so creating normal modes with resonant frequencies related to bond strength and atomic mass of the atoms involved in bonding. For non-linear molecules like styrene-oxide, the degrees of vibrational freedom are 3N-6, where N signifies the number of atoms in the molecule, Thus, as IR spectra are indicative of bonding in the molecule, it is well documented that configurational enantiomers are indistinguishable by IR spectroscopy, due to no change in bonding structure occurring between them. However, the R-styrene oxide calculated spectrum is somewhat offset from the calculated S-styrene oxide spectrum and experimental literature spectra.^[1] ^[1]

This disparity occurs most dramatically in the 2700-3000 cm^-1 region, in which the R-isomer has an absence of characteristic peaks. This is indicative of the static nature of the calculation, which takes into account only the one supplied conformation of the configurational isomer being investigated. In reality, the experimental spectrum occurs with rapid interchange between conformers of the configuration. Thus the total bond energies are averaged over a selection of conformations, and the total bond energies of both R and S-styrene oxide have equivalence. Additionally, this disparity between IR spectra may be indicative of a poor R- or S-styrene model used as input for the NMR calculation.

VCD of S-enantiomer

The VCD of the S-enantiomer was run at the DFT B3LYP 6311++G(2df,p) level of theory also, giving a spectrum as shown.

As reported by G.-J. Kim, D.-W. Park et al.^[29] the VCD of S-(-)-styrene oxide, at the maximum intensity, gives a positive intensity at 1250 cm^-1, whilst R-(+)-styrene oxide gives a negative intensity of equal magnitude at equivalent frequencies. Thus, as the assigned S-enantiomer gives a maximum positive intensity in the present results, some agreement with literature is observed.^[29] However, the maximum peak, lying at 1500 cm^-1 is removed by ~250 cm^-1 from the expected maximum peak, albeit the reduced intensities in the 1200-1000 cm^-1 region agree well with literature.^[29]

VCD of R-enantiomer

The VCD of the R-enantiomer was run at the DFT B3LYP 6311++G(2df,p) level of theory also, giving a spectrum as shown.

As reported by G.-J. Kim, D.-W. Park et al.^[29] the VCD of R-(+)-styrene oxide, at the maximum intensity, gives a negative intensity at 1250 cm^-1, whilst S-(+)-styrene oxide gives a positive intensity of equal magnitude at equivalent frequencies. Thus, as the assigned R-enantiomer gives a maximum positive intensity in the present results, some agreement with literature is observed.^[29] However, the maximum peak, lying at 1500 cm^-1 is removed by ~250 cm^-1 from the expected maximum peak, albeit the reduced intensities in the 1200-1000 cm^-1 region agree well with literature.^[29]

Optical Rotations, ECD and UV-Vis of the Epoxides

For conformational isomers, stereochemistry is only important if one conformation cannot inter-convert freely with the other. Purification of one member of the enantiomeric pair or chiral diastereomers must be achieved to observe an optical rotation; members of the pair cancel each other out if purification is not achieved. Enantiomers of a known compound have optical rotations opposite in sign but identical in intensity. However it is not possible to predict the sign or magnitude of an enantiomer from its stereochemistry. Two diastereomers however have no reported relationship with respect to optical activity sign or magnitude, and have differences in other characteristic properties e.g. reactivity, melting point and solubility that cannot be predicted. For NMR and IR, enantiomers have the same spectra, but diastereomers have different spectra.

Optical Rotation of 1,2-Dihydronapthalene Oxide

The optical rotation of the 1,2-Dihydronapthalene oxide structure can be found from either the 1R,2S- or 1S,2R-enantiomer, as each is of the same magnitude. The lowest energy conformer of each configuration provides the most accurate optical rotation, at room temperature, of that configuration, as most time is spent in the lowest energy conformation, and so at any one time in a given sample, the dominant conformation exists at the energy minimum. The optical rotation was trialled for a number of isomers in order to check reliability of results. The higher energy (1S,2R)-isomer, of 30.68344 kcal/mol, was optimised to the DFT B3LYP 6-31G(d,p) level of theory, the optical rotation was calculated with the 6,311++G(2df,p) basis set. The 30.68344 kcal/mol isomer gave a negative rotation, of magnitude shown below.

[Alpha] ( 5890.0 A) = -155.82⁰
[Alpha] ( 3650.0 A) = -522.16⁰

The 30.2244 kcal/mol isomer, the lowest energy (1S,2R)-isomer, and thus the most accurate approximation for optical rotation was optimised to the DFT B3LYP 6-31G(d,p) level of theory and the optical rotation was calculated with the 6,311++G(2df,p) basis set, giving a negative rotation of magnitude shown below.

[Alpha] ( 5890.0 A) = -155.82⁰
[Alpha] ( 3650.0 A) = -522.15⁰

To increase accuracy of this calculation further the structure was optimised further using the higher force field cc-pVTZ and optical rotation simulation carried out. This returned reduced o.r as below.

[Alpha] ( 5890.0 A) = -155.22⁰
[Alpha] ( 3650.0 A) = -516.50⁰

The negative rotation for the 1S,2R-isomer compares favourably with literature reports,^[33] but indicates the %ee assignment in such literature may be drawn to error due to contaminant molecules present in so-called "enantiopure" references. For example, S. Pedragosa-Moreau et al.^[33] reported a 99% ee with o.r +129 for the (1R,2S)-isomer. This result implies a 100% enantiopure substance of o.r 130.303⁰, a value which is 25.17⁰ and 24.92⁰ lower than that calculated using the 30.2244 kcal/mol isomer, with input optimisations of DFT B3LYP 6-31G(d,p) and cc-pVTZ level of theory respectively. Indeed, the higher energy 30.68344 kcal/mol input isomer at optimised to B3LYP 6-31G(d,p) level of theory also returns an enantiopure o.r greater than the experimental reference. As calculations on the lowest energy isomer at both levels of theory return an enantiopure optical rotation greater in magnitude than the experimental enantiopure reference, this may indicate that the true enantiopure o.r lies significantly higher than the 130.303⁰ reported. However, optical activity is not an individual molecular property, but results from the random distribution of sample molecules. The calculation performed presently is performed on one static molecule only, and does not take into account inter-molecular and packing effects, which may cause changes to the molecular geometry of the oxides and thus cause deviations from the single molecule enantiopure o.r. Additionally, o.r measurements are sensitive to temperature fluctuations, and any disparity between the calculation parameters and the environment of the enantiopure substance may cause the observed experimental o.r reduction.

Optical Rotation of Styrene Oxide

Optical Rotation of S-(-)-Styrene Oxide

Using the NMR of the S-Styrene oxide, the lowest energy structure found in the present study, optimised to the DFT B3LYP 6-31G(d,p) level of theory, the optical rotation was calculated with the 6,311++G(2df,p) basis set. In accordance with literature,^[34] ^[35]this gave a negative rotation for S-styrene oxide, of magnitude shown below.

[Alpha] ( 589.0 nm) = -30.07⁰
[Alpha] ( 365.0 nm) = -93.90⁰

This o.r compared poorly with literature values of ~23⁰,^[34] ^[35] and so the enantiomer was optimised further to the cc-pVTZ level of theory. Using the NMR of this S-Styrene oxide optimised to the DFT B3LYP cc-pVTZ level of theory, the optical rotation was calculated with the 6,311++G(2df,p) basis set. The S-conformer gave a negative rotation, of magnitude shown below.

[Alpha] ( 589.0 nm) = -22.52⁰
Alpha] ( 365.0 nm) = -69.26⁰

The optical rotation at the higher level of theory agrees well with a -22.5⁰ enantiomeric pure reference in literature at 26⁰C^[34], but differs by 1.42⁰ from reports by D. E. White et al. with an enantiomeric pure reference of -23.94⁰ at a temperature of 31⁰C.^[34] ^[36] These differences may arise from temperature differences at measurement of the optical rotation but may also arise from an enantiomeric contamination present for the higher optical rotation. The present optical rotation is reduced compared to those obtained in previous reports due to the averaging effects of conformational transitions in solution, which are not accounted for by the static conformer model. Experimentally, this results in an average optical rotation of the conformations involved in conformational transitions. The present calculation has taken into account only one conformation. To reduce the effects of conformational transitions during computational analysis, the lowest energy conformer found for the S-Styrene oxide product was input into the optical rotation analysis as, this being the lowest energy conformer found presently, it was expected to exist predominantly in solution at any given time, and so give the greatest contribution to the optical rotation. However, the conformation found presently may reside at a local energy minima, in which case the trialed conformer would not be present as the predominant conformation.

Optical Rotation of R-(+)-Styrene Oxide

Using the NMR of R-Styrene oxide optimised to the DFT B3LYP 6-31G(d,p) level of theory, the optical rotation was calculated with the 6.311++G(2df,p) basis set. The higher energy 21.61547 kcal/mol configuration gave a positive rotation, of magnitude shown below.

[Alpha] ( 589.0 A) = 30.17⁰ [Alpha] ( 365.0 A) = 94.24⁰

Using the NMR of Styrene oxide optimised to the DFT B3LYP cc-pVTZ level of theory, the optical rotation was calculated with the 6,311++G(2df,p) basis set. The higher energy 21.61547 kcal/mol configuration gave a positive rotation, of magnitude shown below.

[Alpha] ( 589.0 A) = 22.47⁰ [Alpha] ( 365.0 A) = 69.10⁰

The R-styrene oxide conformer found with lower energy, 21.61506 kcal/mol was optimised to the DFT B3LYP 6-31G(d,p) level of theory, the optical rotation was calculated with 6.311++G(2df,p) basis set.

[Alpha] ( 589.0 A) = 30.43⁰ [Alpha] ( 365.0 A) = 95.05⁰

This conformer was optimised to the DFT B3LYP cc-pVTZ level of theory, and the optical rotation was calculated with 6.311++G(2df,p) basis set, giving a closer fit with literature.^[37]

[Alpha] ( 589.0 A) = 23.06⁰ [Alpha] ( 365.0 A) = 71.02⁰

In general for the Styrene oxide enantiomers, the lower energy conformers give the best fit with literature, and increasing the optimisation level of theory to the cc-pVTZ level increases the agreement with literature.^[37]

ECD and UV-Vis Simulations

Electronic Circular Dichroism spectroscopy (ECD) can be used to determine the absolute structure of solid and solution-phase molecules. For determining molecular 3D structure, configuration and conformation, it is a sensitive, quick and reliable technique, provided that the substance has chirality, is non-racemic, and absorbs circularly polarized light (CPL) in 180 - 1100 nm range available.^[38]

ECD and UV-Vis of 1,2-Dihydronapthalene Oxide

ECD and UV-Vis simulation were run on the 30.22441 kcal/mol configuraiton isomer, at DFT B3LYP 6-31G level of theory giving spectra as shown below.

UV-vis napthalane lowest energy conformer.svg

Excitation Energy (nm) = 192.5000000000 ɛ = 57629.5162835934 d(epsilon)/d(excitation energy) = -294.5415960797

Ecd spectrum napthalene lowest energy.svg

Excitation Energy (nm)= 196.0000000000 ∆ɛ = 9.0192453436

ECD and UV-Vis simulations were also run on the lowest energy conformer, the 30.2244 kcal/mol of the (-)-1,2-dihydronapthalene oxide configuration, which was deemed to be a more accurate representation of the molecule in solution. Noted are the maxima and minima for the relevant spectra of the structure optimised to the B3LYP 6-31G(d,p) level of theory are as below.

UV-Vis spectrum:

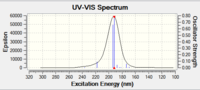
Excitation Energy (nm)= 192.02
Oscillator Strength = 0.7778

Comparing this UV-Vis maximum with that obtained for the higher energy (+)-isomer at the same level of theory, there is a 0.48 nm decrease in absorption maximum associated with the 0.00001 kcal/mol decrease in initial input energy.

ECD spectrum:

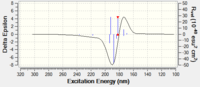
Excitation Energy (nm)= 187.58
R_vel (10^-40 esu²cm² = -47.1
∆ɛ = ~-8

Excitation Energy (nm)= 173.5
R_vel (10^-40 esu²cm² = 26.872
∆ɛ = ~4.5

To increase the accuracy of these calculations, the structure was optimised to B3LYP cc-pVTZ level of theory and ECD and UV-Vis simulations run. Noted are the maxima and minima for the relevant spectra of the structure optimised to the cc-pVTZ level of theory are as below.

UV-Vis spectrum:

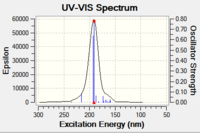
Excitation Energy (nm)= 190.84
Oscillator Strength = 0.7719

Thus increasing the force field increases the energy of the maximum absorption excitation energy, which is to be expected given the reduction in total energy that the cc-pVTZ force field brings about during optimisation c.f. the 6-31G force field.

ECD spectrum:

Excitation Energy (nm)= 158.78
R_vel (10^-40 esu²cm² = 0.441
∆ɛ = ~-3

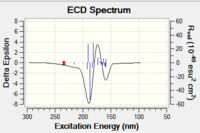
Excitation Energy (nm)= 173.53
R_vel (10^-40 esu²cm² = 7.1378
∆ɛ = ~3

Excitation Energy (nm)= 187.18
R_vel (10^-40 esu²cm² = -530.165
∆ɛ = ~-8

At the higher level of theory, one extra peak at a higher energy of 158.78 nm is observed, and all peaks are shifted to lower energy.

The ECD spectra are in general the mirror image of the UV-Vis spectrum, as expected, and each configurational isomer ECD spectrum is the mirror image of the other. However, no literature could be found for either enantiomer to compare with experimental values. Literature reports involving napthalene derivatives exhibit ECD peaks within the 200-250 nm region.^[39] The calculated values at the DFT B3LYP 6-31G level of theory lie in the 150-200 nm region, and thus provide a reasonable similarity given the errors associated with such a comparison.

ECD and UV-Vis of Styrene Oxide

Using the NMR calculation carried out on the R-styrene oxide highest energy configurational isomer, at the DFT B3LYP 6-31G(d,p) level of theory, ECD and UV-Vis simulations were run, giving results as shown below.

UV-Vis Spectrum

ʎ_max Excitation Energy (nm) = 187.98
Oscillator Strenght = 0.867
∆ɛ = ~59000

ECD Spectrum

ʎ_max Excitation Energy (nm)= 185.54
∆ɛ = ~-12
R_vel = ~-30

ʎ_max Excitation Energy (nm)= 160.09
∆ɛ = ~15
R_vel = ~40

Using the NMR calculation carried out on the S-styrene oxide configurational isomer, of lowest energy, at the DFT B3LYP 6-31G(d,p) level of theory, ECD and UV-Vis simulations were run, giving results as shown below.

UV-Vis Spectrum

ʎ_max Excitation Energy (nm) = 188.2400000000
∆ɛ = 58894.6631990984
d∆ɛ/dExcitation Energy =320.5154439262

ECD Spectrum

ʎ_max Excitation Energy (nm)= 185.6000000000
∆ɛ = 13.8016611316
d∆ɛ/dExcitation Energy = -0.4784170592

ʎ_min Excitation Energy (nm) = 160.0800000000
∆ɛ = -15.8501295345
d∆ɛ/dExcitation Energy = 0.3810660432

Suggesting New Candidates for Investigation=

A suitable epoxide of o.r > 500 or < 500 is provided by 2-(4-methylphenyl)-3-phenyl oxirane trans-(2R,3R)-2-(4-methylphenyl)-3-phenyl oxirane [Alpha] ( 5890.0 A) = -320.35˚ [Alpha] ( 4360.0 A) = -730.74˚

cis [Alpha] ( 5890.0 A) = -25.48 deg [Alpha] ( 4360.0 A) = -49.25 deg

Dansette,P.M. et al. Tetrahedron, 1976 , vol. 32, p. 2071 - 2074

The trans-(2R,3R)-2-(4-methylphenyl)-3-phenyl oxirane was optimised to a minimum in Avogadro using the MMF94s force field and conjugate gradients. The structure and parameters of the optimised molecule are shown below.

Trans methyl stilbene for hpc.cml

Energy Contribution	Energy (kcal/mol)
Total Electrostatic Energy	5.04177
Total Out-of-Palne Bending Energy	0.0201
Total Torsional Energy	2.17991
Total Stretch Bending Energy	-1.50356
Total Angle Bending Energy	2.83423
Total Bond Stretching Energy	3.9429
Total Energy	41.55575

This structure was submitted to optimisation at the DFT B3LYP 6-31G(d,p) level of theory, giving a structure and energy as shown below.

Sum of electronic and zero-point Energies= -655.026348

Sum of electronic and thermal Energies=              -655.012762
Sum of electronic and thermal Enthalpies=            -655.011818
Sum of electronic and thermal Free Energies=         -655.068821

The enantiomeric (1S,2R)-cis-2-(4-methylbenzenyl)-3-phenyl-oxirane, with a lower reported optical rotation, was optimised in Avogadro with the MMFF94s force field using the conjugate gradient algorithm. The structure and parameters of the lowest energy structure obtained using this technique are as below.

Trans methyl stilbene opt 4 (cis) new one.cml

'
Energy Contribution	Energy (kcal/mol)
Total Electrostatic Energy	6.56941
Total Van der Waals Energy	28.65841
Total Out-of-Palne Bending Energy	0.02091
Total Torsional Energy	2.1782
Total Stretch Bending Energy	-1.3851
Total Angle Bending Energy	3.20829
Total Bond Stretching Energy	4.08582
Total Energy	43.33594

NMR analysis was carried out, giving good agreement with literature for most carbon shifts, as documented below.

Carbon Number	δcalc (ppm)	δexp (ppm)	∆δcalc-exp (ppm)	Average ∆δcalc-exp (ppm)	Mode ∆δcalc-exp (ppm)
C1	122.9778008	125.5	-2.522199225	-4.017924319	-7.153745456
C2	123.513071	128.5	-4.986928969
C3	123.0827678	128.2	-5.117232162
C4	124.1918224	129.2	-5.008177643
C5	118.2462545	125.4	-7.153745456
C6	134.2028056	138.2	-3.997194358
C7	124.2666619	129.2	-4.933338102
C8	123.100	128.2	-5.100009147
C9	131.2212506	138.2	-6.978749362
C10	118.4044517	125.4	-6.99554825
C11	124.9491655	137.2	-12.25083451
C12	134.7213106	138.2	-3.478689364
C13	66.42459374	62.8	3.624593736
C14	66.27088104	62.7	3.57088104
C16	22.25830698	21.2	1.058306982

This was optimised to the DFT B3LYP 6-31G(d,p) level of theory, giving a structure of energetic parameters, expressed in Hartree/particle, as below.

Thermal correction to Gibbs Free Energy=               0.204857

Sum of electronic and zero-point Energies=           -655.023912

Sum of electronic and thermal Energies=              -655.010405

Sum of electronic and thermal Enthalpies=            -655.009460

Sum of electronic and thermal Free Energies=         -655.066618

↑ ^1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 ^1.6 W. T. Klooster , T. F. Koetzle , P. E. M. Siegbahn , T. B. Richardson , and R. H. Crabtree, "Study of the N-H···H-B Dihydrogen Bond Including the Crystal Structure of BH₃NH₃ by Neutron Diffraction", J. Am. Chem. Soc., 1999, 121, 6337–6343.DOI:10.1021/ja9825332 Cite error: Invalid <ref> tag; name "ja9825332" defined multiple times with different content
↑ ^2.0 ^2.1 ^2.2 J. Sauer, R. Sustmann, Angew. Chem. Int. Ed. Engl., 1980, 19, 779 - 807.DOI:[1] Cite error: Invalid <ref> tag; name "ja9825334" defined multiple times with different content
↑ K. Alder, G. Stein , Angew. Chem., 1937, 50, 510.DOI:[2]
↑ L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc., 1990, 112, 277-283.DOI:10.1021/ja9825332
↑ ^5.0 ^5.1 ^5.2 ^5.3 S. W. Elmore, L. Paquette, Tet. Lett., 1991, 319, 1891DOI:10.1016/S0040-4039(00)92617-0
↑ ^6.0 ^6.1 W. F. Maier, P.-V. R. Schleyer,J. Am. Chem. Soc., 1981, 103, 1891DOI:10.1021/ja00398a003
↑ C. Braddock, H. S. Rzepa, J. Nat. Prod., 2008, 71, 728-730DOI:10.1021/np0705918
↑ M. Durík, V. Langer, D. Gyepesová, J. Micová, B. Steiner M. Koós, Acta Cryst.,2001,E57, 672-674DOI:10.1107/S160053680101073X 10.1107/S160053680101073X
↑ ^9.0 ^9.1 Z.-X. Wang , S. M. Miller, O. P. Anderson, Y. Shi, J. Org. Chem.,2001, 66, 2, 521–530.DOI:10.1021/jo001343i 10.1021/jo001343i
↑ ^10.0 ^10.1 ^10.2 R. V. Stick, S. J. Williams, Carbohydrates, Amsterdam, Elsevier, 2009.Template:ISBN Cite error: Invalid <ref> tag; name "ja9825335" defined multiple times with different content
↑ ^11.0 ^11.1 ^11.2 J. Clayden, N. Greeves, S. Warren, P. Wothers, Organic Chemistry, Oxford University Press,2nd Edition, 2012, 1126-1131.Template:ISBN
↑ Z.-X. Wang , S. M. Miller, O. P. Anderson, Y. Shi, J. Org. Chem.,2001, 66, 2, 521–530.DOI:10.1021/jo001343i 10.1021/jo001343i
↑ J. W. Yoon, T.-S. Yoon, S. W. Lee, W. Shin, Acta Cryst.,1999, C55, 1766-1769 .DOI:10.1107/S0108270199009397
↑ F. R. Fronczek, X. R. J. Bu, Private Comm.,2002DOI:[3]
↑ ^15.0 ^15.1 E. Anslyn, Modern Physical Organic Chemistry, 2004, Sausalito, CA, University ScienceTemplate:ISBN Cite error: Invalid <ref> tag; name "ja9825332123" defined multiple times with different content
↑ Z.-X. Wang,Y. Shi, J. Org. Chem. 1997, 62, 8622-8623DOI:S0022-3263(97)01701-5
↑ ^17.0 ^17.1 ^17.2 ^17.3 G.-A. Cao, Z.-X. Wang, Y. Tu, Y. Shi, Tetrahedron Letters, 1998, 39, 25, 4425–4428DOI:10.1016/S0040-4039(98)00838-7 Cite error: Invalid <ref> tag; name "ja982533672123" defined multiple times with different content
↑ M. Hickey, D. Goeddel, Z. Crane, Y. Shi, Proc. Natl. Acad. Sci. USA; 2004, 101, 16, 5794–5798DOI:10.1073/pnas.0307548101
↑ J. L. Arbour, H. S. Rzepa, J. Contreras-García, L. A. Adrio, E. M. Barreiro, K. K. Hii, Chemistry - A European Journal, 2012, 18, 36, 11317–11324DOI:10.1002/chem.201200547
↑ G. A. Morris, S. B. T. Nguyen, J. T. Hupp, J. Mol. Cat. A: Chemical 174, 2001, 15–20DOI:S1381-1169(01)00165-0
↑ W. Zhang, J. L. Loebach, S. R. Wilson, E. N. Jacobsen, J. Am. Chem. Soc., 1990, 112, 7, 2801-2803 DOI:10.1021/ja00163a052
↑ M. Palucki, P. J. Pospisil, W. Zhang, E. N. Jacobsen, J. Am. Chem. SOC. 1994,116, 9333-9334DOI:10.1021/ja00099a062
↑ C. Altona, J. H. Ippel, A. J. A. W. Hoekzema, C. Erkelens, M. Groesbeek, L. A. Donders, A. Lambertus, Magnetic Resonance in Chemistry, 1989 , 27, 6, 564 - 576DOI:10.1002/mrc.1260270609
↑ ^24.0 ^24.1 P. C. Bulman Page, B. R. Buckley ,H. Heaney, A. J. Blacker, Org. Lett., 2005, 7, 3, 375–377DOI:10.1021/ol047836h
↑ ^25.0 ^25.1 ^25.2 L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc., 1990, 112, 277-283 DOI:10.1021/ja00157a043
↑ ^26.0 ^26.1 ^26.2 D. Xiong, X. Hu, S. Wang, C.-X. Miao, C. Xia, W. E. Sun, J. Org. Chem., 2011, 23, 4289–4292DOI:[4]
↑ ^27.0 ^27.1 P. C. B. Page, B. R. Buckley, H. Heaney , A. J. Blacker, Org. Lett., 2005, 7, 3, 375–377 DOI:10.1021/ol047836h
↑ C. Guo, R. D. Shah, R. K. Dukor, X. Cao, T. B. Freedman , L. A. Nafie, Anal. Chem., 2004, 76, 23,6956–6966DOI:10.1021/ac049366a
↑ ^29.0 ^29.1 ^29.2 ^29.3 ^29.4 ^29.5 ^29.6 G.-J.Kim, D.-W. Park, Y.-S. Tak, Catalysis Letters, 2000, 65, 1-3, 127-133DOI:10.1023/A:1019040532103
↑ ^30.0 ^30.1 D. Xiong, X. Hu, S. Wang, Shoufeng, C.-X. Miao, C. Xia, W. Sun, European Journal of Organic Chemistry, 2011 , 23, 4289 - 4292
↑ Y. Kon, H. Hachiya, Y. Ono, T. Matsumoto, K. Sato, Synthesis, 2011, 7, 1092-1098DOI:[5]
↑ K. Sarma,N. Bhati, N. Borthakur, A. Goswami, Tetrahedron, 2007, 63, 36, 8735,-8741
↑ ^33.0 ^33.1 S. Pedragosa-Moreau, A Archelas, R Furstoss, Tetrahedron, 1996, 52, 13, 4593–4606 DOI:10.1016/0040-4020(96)00135-4
↑ ^34.0 ^34.1 ^34.2 ^34.3 M. Hayashi, H. Miwata, N. Oguni, J. Chem. Soc., Perkin Transactions 1: Organic and Bio-Organic Chemistry, 1991, 5, 1167-1171 DOI:[6]
↑ ^35.0 ^35.1 V. Capriati, S. Florio, R. Luisi, A. Salomone, Org. Lett., 2002, 4, 14, 244-2448DOI:10.1021/ja9825332
↑ D. E. White, E. N. Jacobsen, Tetrahedron: Asymmetry, 2003, 14, 22, 3633-3638DOI:10.1016/j.tetasy.2003.09.024
↑ ^37.0 ^37.1 R. Imae, N. Itoh, H. Toda, Tetrahedron Asymm., 2012, 23, 22-23, 1542-1549DOI:[7]
↑ P. J. Stephens, F. J. Devlin, J. R. Cheeseman, VCD Spectroscopy for Organic Chemists, CRC Press, 2012, 1-30Template:ISBN
↑ B. M. Bulheller, G. D. Pantoş, J. K. M. Sanders, J. D. Hirst, Phys. Chem. Chem. Phys., 2009,11, 6060-6065DOI:10.1039/B905187B

[ja9825332-1] 1.0 ^1.1 ^1.2 ^1.3 ^1.4 ^1.5 ^1.6 W. T. Klooster , T. F. Koetzle , P. E. M. Siegbahn , T. B. Richardson , and R. H. Crabtree, "Study of the N-H···H-B Dihydrogen Bond Including the Crystal Structure of BH₃NH₃ by Neutron Diffraction", J. Am. Chem. Soc., 1999, 121, 6337–6343.DOI:10.1021/ja9825332 Cite error: Invalid <ref> tag; name "ja9825332" defined multiple times with different content

[ja9825334-2] 2.0 ^2.1 ^2.2 J. Sauer, R. Sustmann, Angew. Chem. Int. Ed. Engl., 1980, 19, 779 - 807.DOI:[1] Cite error: Invalid <ref> tag; name "ja9825334" defined multiple times with different content

[ja9825333-3] K. Alder, G. Stein , Angew. Chem., 1937, 50, 510.DOI:[2]

[ja9825301-4] L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc., 1990, 112, 277-283.DOI:10.1021/ja9825332

[ja98253986-5] 5.0 ^5.1 ^5.2 ^5.3 S. W. Elmore, L. Paquette, Tet. Lett., 1991, 319, 1891DOI:10.1016/S0040-4039(00)92617-0

[ja98253980-6] 6.0 ^6.1 W. F. Maier, P.-V. R. Schleyer,J. Am. Chem. Soc., 1981, 103, 1891DOI:10.1021/ja00398a003

[ja9825304-7] C. Braddock, H. S. Rzepa, J. Nat. Prod., 2008, 71, 728-730DOI:10.1021/np0705918

[ja9825311-8] M. Durík, V. Langer, D. Gyepesová, J. Micová, B. Steiner M. Koós, Acta Cryst.,2001,E57, 672-674DOI:10.1107/S160053680101073X 10.1107/S160053680101073X

[ja9825312-9] 9.0 ^9.1 Z.-X. Wang , S. M. Miller, O. P. Anderson, Y. Shi, J. Org. Chem.,2001, 66, 2, 521–530.DOI:10.1021/jo001343i 10.1021/jo001343i

[ja9825335-10] 10.0 ^10.1 ^10.2 R. V. Stick, S. J. Williams, Carbohydrates, Amsterdam, Elsevier, 2009.Template:ISBN Cite error: Invalid <ref> tag; name "ja9825335" defined multiple times with different content

[ja9825309-11] 11.0 ^11.1 ^11.2 J. Clayden, N. Greeves, S. Warren, P. Wothers, Organic Chemistry, Oxford University Press,2nd Edition, 2012, 1126-1131.Template:ISBN

[ja98253709-12] Z.-X. Wang , S. M. Miller, O. P. Anderson, Y. Shi, J. Org. Chem.,2001, 66, 2, 521–530.DOI:10.1021/jo001343i 10.1021/jo001343i

[ja9825398-13] J. W. Yoon, T.-S. Yoon, S. W. Lee, W. Shin, Acta Cryst.,1999, C55, 1766-1769 .DOI:10.1107/S0108270199009397

[ja9825360-14] F. R. Fronczek, X. R. J. Bu, Private Comm.,2002DOI:[3]

[ja9825332123-15] 15.0 ^15.1 E. Anslyn, Modern Physical Organic Chemistry, 2004, Sausalito, CA, University ScienceTemplate:ISBN Cite error: Invalid <ref> tag; name "ja9825332123" defined multiple times with different content

[ja979082533672123-16] Z.-X. Wang,Y. Shi, J. Org. Chem. 1997, 62, 8622-8623DOI:S0022-3263(97)01701-5

[ja982533672123-17] 17.0 ^17.1 ^17.2 ^17.3 G.-A. Cao, Z.-X. Wang, Y. Tu, Y. Shi, Tetrahedron Letters, 1998, 39, 25, 4425–4428DOI:10.1016/S0040-4039(98)00838-7 Cite error: Invalid <ref> tag; name "ja982533672123" defined multiple times with different content

[ja9825890733892-18] M. Hickey, D. Goeddel, Z. Crane, Y. Shi, Proc. Natl. Acad. Sci. USA; 2004, 101, 16, 5794–5798DOI:10.1073/pnas.0307548101

[ja982589077865332-19] J. L. Arbour, H. S. Rzepa, J. Contreras-García, L. A. Adrio, E. M. Barreiro, K. K. Hii, Chemistry - A European Journal, 2012, 18, 36, 11317–11324DOI:10.1002/chem.201200547

[ja982533672176823-20] G. A. Morris, S. B. T. Nguyen, J. T. Hupp, J. Mol. Cat. A: Chemical 174, 2001, 15–20DOI:S1381-1169(01)00165-0

[ja9825336723421176823-21] W. Zhang, J. L. Loebach, S. R. Wilson, E. N. Jacobsen, J. Am. Chem. Soc., 1990, 112, 7, 2801-2803 DOI:10.1021/ja00163a052

[ja98253367217341266823-22] M. Palucki, P. J. Pospisil, W. Zhang, E. N. Jacobsen, J. Am. Chem. SOC. 1994,116, 9333-9334DOI:10.1021/ja00099a062

[ja98253989-23] C. Altona, J. H. Ippel, A. J. A. W. Hoekzema, C. Erkelens, M. Groesbeek, L. A. Donders, A. Lambertus, Magnetic Resonance in Chemistry, 1989 , 27, 6, 564 - 576DOI:10.1002/mrc.1260270609

[ja98253987632-24] 24.0 ^24.1 P. C. Bulman Page, B. R. Buckley ,H. Heaney, A. J. Blacker, Org. Lett., 2005, 7, 3, 375–377DOI:10.1021/ol047836h

[ja9825397867632-25] 25.0 ^25.1 ^25.2 L. Paquette, N. A. Pegg, D. Toops, G. D. Maynard, R. D. Rogers, J. Am. Chem. Soc., 1990, 112, 277-283 DOI:10.1021/ja00157a043

[ja98253367842-26] 26.0 ^26.1 ^26.2 D. Xiong, X. Hu, S. Wang, C.-X. Miao, C. Xia, W. E. Sun, J. Org. Chem., 2011, 23, 4289–4292DOI:[4]

[ja982533670875-27] 27.0 ^27.1 P. C. B. Page, B. R. Buckley, H. Heaney , A. J. Blacker, Org. Lett., 2005, 7, 3, 375–377 DOI:10.1021/ol047836h

[ja982533289701-28] C. Guo, R. D. Shah, R. K. Dukor, X. Cao, T. B. Freedman , L. A. Nafie, Anal. Chem., 2004, 76, 23,6956–6966DOI:10.1021/ac049366a

[ja98253328970-29] 29.0 ^29.1 ^29.2 ^29.3 ^29.4 ^29.5 ^29.6 G.-J.Kim, D.-W. Park, Y.-S. Tak, Catalysis Letters, 2000, 65, 1-3, 127-133DOI:10.1023/A:1019040532103

[ja9824560-30] 30.0 ^30.1 D. Xiong, X. Hu, S. Wang, Shoufeng, C.-X. Miao, C. Xia, W. Sun, European Journal of Organic Chemistry, 2011 , 23, 4289 - 4292

[ja98254567-31] Y. Kon, H. Hachiya, Y. Ono, T. Matsumoto, K. Sato, Synthesis, 2011, 7, 1092-1098DOI:[5]

[ja98253234-32] K. Sarma,N. Bhati, N. Borthakur, A. Goswami, Tetrahedron, 2007, 63, 36, 8735,-8741

[ja9825393-33] 33.0 ^33.1 S. Pedragosa-Moreau, A Archelas, R Furstoss, Tetrahedron, 1996, 52, 13, 4593–4606 DOI:10.1016/0040-4020(96)00135-4

[ja9878654925332-34] 34.0 ^34.1 ^34.2 ^34.3 M. Hayashi, H. Miwata, N. Oguni, J. Chem. Soc., Perkin Transactions 1: Organic and Bio-Organic Chemistry, 1991, 5, 1167-1171 DOI:[6]

[ja9825465332-35] 35.0 ^35.1 V. Capriati, S. Florio, R. Luisi, A. Salomone, Org. Lett., 2002, 4, 14, 244-2448DOI:10.1021/ja9825332

[ja98254653378962-36] D. E. White, E. N. Jacobsen, Tetrahedron: Asymmetry, 2003, 14, 22, 3633-3638DOI:10.1016/j.tetasy.2003.09.024

[ja982587869332-37] 37.0 ^37.1 R. Imae, N. Itoh, H. Toda, Tetrahedron Asymm., 2012, 23, 22-23, 1542-1549DOI:[7]

[ja982536750-38] P. J. Stephens, F. J. Devlin, J. R. Cheeseman, VCD Spectroscopy for Organic Chemists, CRC Press, 2012, 1-30Template:ISBN

[ja982531223-39] B. M. Bulheller, G. D. Pantoş, J. K. M. Sanders, J. D. Hirst, Phys. Chem. Chem. Phys., 2009,11, 6060-6065DOI:10.1039/B905187B

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

Part 1

Thermodynamic Analysis of Cyclopentadiene Dimerisation and Hydrogenation Products

Molecule 2

Conformations of an Intermediate in Taxol Synthesis

Carbonyl-down Atropisomers

ChemBio3D Optimisations

Carbonyl-up Atropisomers

Comparison of Carbonyl-Up and Carbonyl-Down Atropisomers

Dithiol, Methylated Derivative of Taxol

NMR Analysis of dithiol Taxol Derivative

Modelling the Sulphur bonded Carbon correction constant

Analysis of Taxol Derivative NMR calculations

Part 2

Crystallographic Data

NELQEA

NELQEA01

Molecule 23,[Mn(III)(salen)(Cl)],(1R,2R)-(-)-[Bis(3,5-di-tert-butylsalicylidene)-1,2-cyclohexanediamine]chloromanganese(III), An Intermediate in Jacobsen's Catalyst Synthesis

TOVNIB01

TOVNIB02

Analysis of the Transition State for Shi Catalyst Catalysed Epoxidation of Styrene

NCI and QTAIM Analysis of the S-styrene series

R-styrene series QTAIM Lowest Energy Transition State

Analysis of the Transition State for Jacobsen's Catalyst Catalysed Epoxidation of Styrene

S-styrene series QTAIM Lowest Energy Transition State

R-styrene series QTAIM Lowest Energy Transition State

Analysis of the Transition State for Shi Catalyst Catalysed Epoxidation of 1,2-Dihydronapthalene

S,R-Dihydronapthalene oxide series QTAIM Highest Energy Transition State

S,R-Dihydronapthalene oxide series QTAIM Lowest Energy Transition State

NMR and Modelling of Alkenes and the Associated Epoxides

1,2-Dihydronapthalene Oxide

NMR

Calculation of Oxide Correction Constants

Correction Factors

1,2-dihydronapthalene oxide NMR

Higher Level of Theory

A Higher Energy Enantiomer, 30.22441 kcal/mol input energy

1H NMR data

Comparison of B3LYP 6-31G(d,p) optimised structure with MMFF94s force field, conjugate gradient optimisation algorithm

Comparison of 1H NMR data with (+)-1,2-Dihydronapthalene Oxide Literature

Carbon NMR Comparison with (-)-Rotamer

(-)-1,2-Dihydronapthalene oxide Literature Comparison

13C NMR data=

Comparison of 13C NMR data with Literature

Repeat of NMR Analysis Using a Different Conformer and Higher Level of Theory

30.68344 kcal/mol isomer at the 6-31G (d,p) level of theory

30.68344 kcal/mol isomerAt the cc-pVTZ level of theory

IR and VCD analysis

Styrene oxide Configurations

NMR analysis of S-styrene oxide

Comparison of S-styrene Oxide with Literature

NMR analysis of R-Styrene Oxide Lowest Energy Conformer

Comparison of spectra with (S)-Styrene oxide

Comparison of spectra with (R)-Styrene oxide

IR and VCD analysis of styrene oxide

S-Styrene Oxide

=R-Styrene Oxide

VCD of S-enantiomer

VCD of R-enantiomer

Optical Rotations, ECD and UV-Vis of the Epoxides

Optical Rotation of 1,2-Dihydronapthalene Oxide

Optical Rotation of Styrene Oxide

Optical Rotation of S-(-)-Styrene Oxide

Optical Rotation of R-(+)-Styrene Oxide

ECD and UV-Vis Simulations

ECD and UV-Vis of 1,2-Dihydronapthalene Oxide

ECD and UV-Vis of Styrene Oxide

Suggesting New Candidates for Investigation=

¹H NMR data

Comparison of ¹H NMR data with (+)-1,2-Dihydronapthalene Oxide Literature

¹³C NMR data=

Comparison of ¹³C NMR data with Literature