Rep:Mod:19970410
NH3
Basic properties of NH3
Calculation method:RB3LYP
Basis set:6-31G(d,p)
Final energy:-56.55776873 a.u.
RMS gradient:0.00000485 a.u.
Point group:C3v
N-H distance:1.01798 Å
The literature value of N-H distance is 1.012 Å [1]
H-N-H Bond angle:105.74115°
The literature value of H-N-H Bond angle is 106.7° [2]
Item Table of NH3
[here]
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986277D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Diagram of NH3
NH3 molecule |
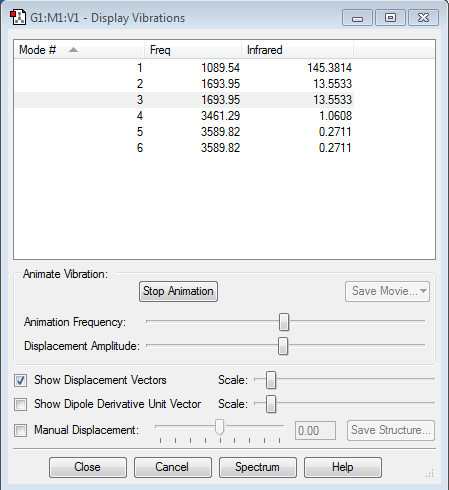
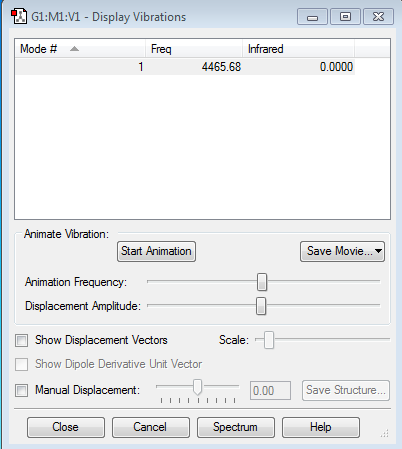
Vibrations
Mode of different vibrations
Vibration images
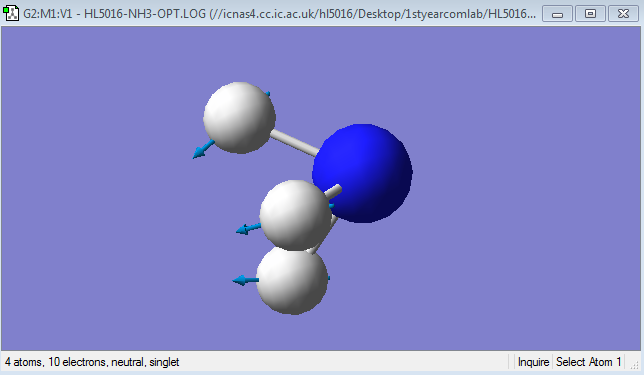
Mode 1
Frequency: 1089.54Hz
Intensity:145.3814
Type:Bending
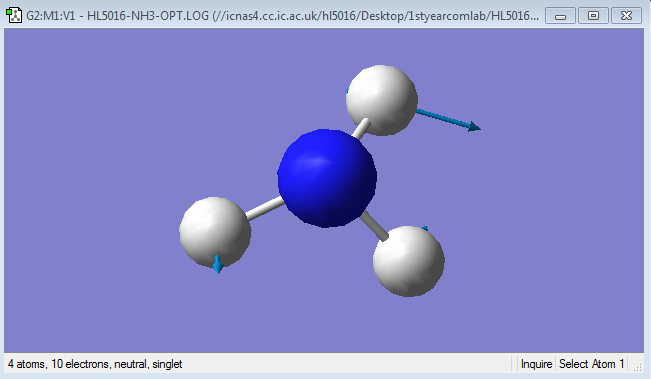
Mode 2
Frequency: 1693.95Hz
Intensity:13.5533
Type:Bending
Mode 3
Frequency: 1693.95Hz
Intensity:13.5533
Type:Bending
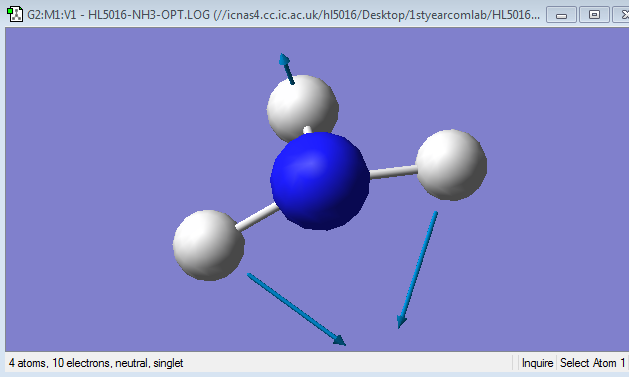
Mode 4
Frequency: 3461.29Hz
Intensity:1.0608
Type:stretching
Mode 5
Frequency: 3589.82Hz
Intensity:0.2711
Type:stretching
Mode 6
Frequency: 3589.82Hz
Intensity:0.2711
Type:stretching
How many modes do you expect from the 3N-6 rule?
For the rule 3N-6, N represents the number of atoms which is 4 in NH3, So the expected number of modes should be 3*4-6=6.
Which modes are degenerate (ie have the same energy)?
Mode 2 and mode 3 are degenerate; Mode 5 and mode 6 are degenerate since they absorb Infrad red with the same frequency.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Mode 1,2 and 3 are "bending" vibrations;Mode 4,5 and 6 are "bond stretch" vibrations.
Which mode is highly symmetric?
Mode 4 is highly symmetric.
One mode is known as the "umbrella" mode, which one is this?
Mode 1 is the "umbrella" mode.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
4 bands will be expected, but from the spectrum, the band can be observed is only 2. The dipole moment of the several modes are too low, thus the intensity is quite low, so the spectrum do no show them.
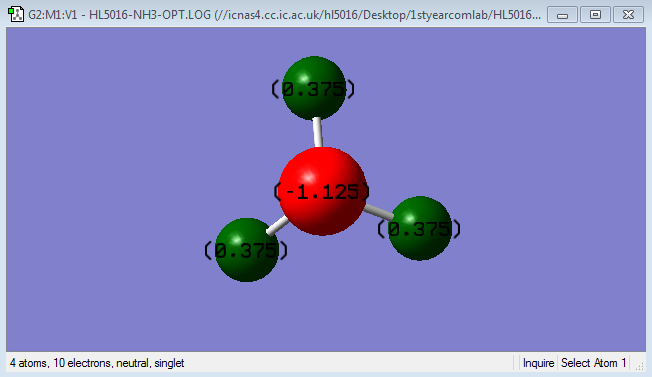
Charge Distribution
The charge on the N-atom is -1.125;
The charge on the H-atom is +0.375.
Because N-atom has a bigger electronegativity than H-atom, so electrons are 'pulled' towards N-atom. The concept electronegativity is a chemical properties that means the ability to attract electrons towards itself.
H2
Basic properities of H2
Calculation method:RB3LYP
Basis set:6-31G(d,p)
Final energy:-1.17853936 a.u.
RMS gradient:0.00000017 a.u.
Point group:D∞h
H-H distance:0.74279 Å
The literature value of H-H bond distance is 0.74 Å [3]
H-H Bond angle:180 °
Item Table of H2
[here]
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Diagram of H2
H2 molecule |
Vibrations
Mode of Vibrations
Vibration images
Mode 1
Frequency:4465.68Hz
Intensity:0
Type:stretching
Since the H2 molecule have no dipole moment, so they will not absorb IR, thus the intensity is 0.
Charge Distribution
The charge on the N-atom is 0.00;
The charge on the H-atom is 0.00.
Because H-atom has a same electronegativity with the H-atom, so electrons are 'pulled' equally towards themselves. The concept electronegativity is a chemical properities that means the ability to attract electrons towards itself.
N2
Basic properties of N2
Calculation method:RB3LYP
Basis set:6-31G(d,p)
Final energy:-109.52412868 a.u.
RMS gradient:0.00000060 a.u.
Point group:C∞h
N-N distance:1.10550 Å
N-N Bond angle:105.74115 °
Item Table of N2
[here]
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401031D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Diagram of N2
N2 molecule |
Vibrations
Mode of different vibrations
Vibration images
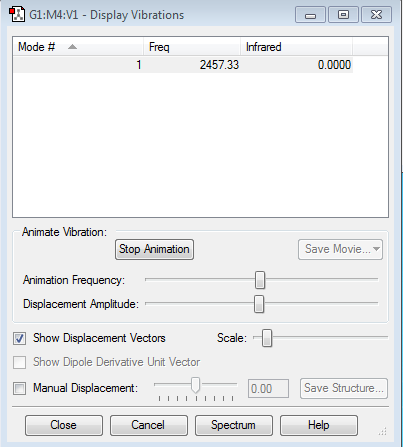
Mode 1
Frequency:2457.33Hz
Intensity:0
Type: stretching
Since the N2 molecule have no dipole moment, so they will not absorb IR, thus the intensity is 0.
Charge Distribution
The charge on the N-atom is 0.00;
The charge on the H-atom is 0.00.
Because N-atom has a same electronegativity with the N-atom, so electrons are 'pulled' equally towards themselves. The concept electronegativity is a chemical properities that means the ability to attract electrons towards itself.
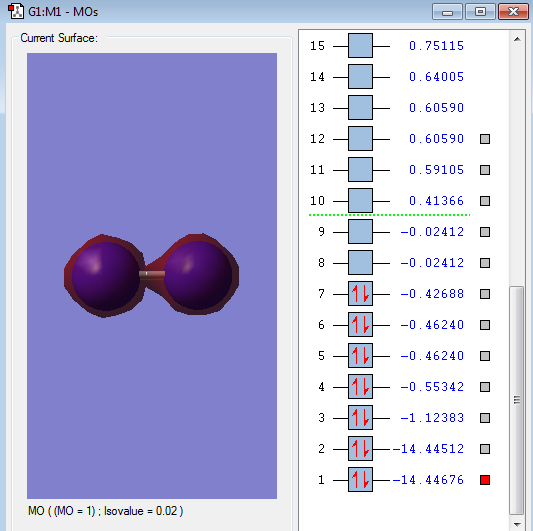
Molecular Orbitals of N2
MO diagram
MO images
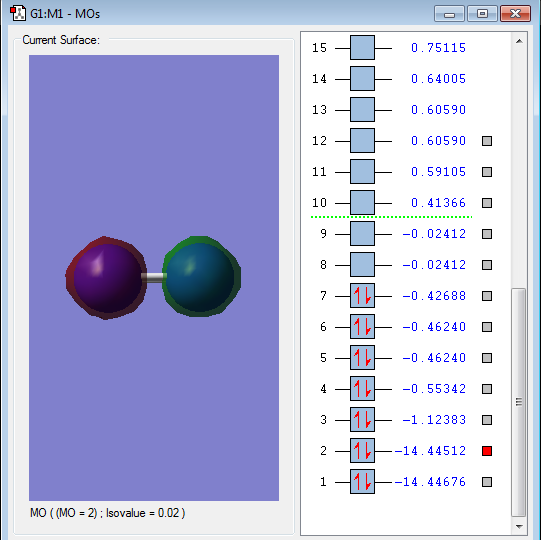
Type of orbital: 1s-1s bonding orbital
Energy of orbital:-14.44676 a.u.
Description:This is the 1s-1s bonding orbital. From the diagram, there is little overlap of 1s-1s AOs and has a very low energy. These 2 features indicate the little contribution of chemical bonding. Because the 1s AOs is very close to nucleus, the electrons will be held so tightly, thus 1s AOs are very hard to overlap.
Type of orbital: 1s-1s anti-bonding π orbital
Energy of orbital:-14.44512 a.u.
Description: This is anti-bonding orbital with low contribution to the formation of chemical bonding. The energy of this MO is too low that means there is almost no contribution of bond formation.
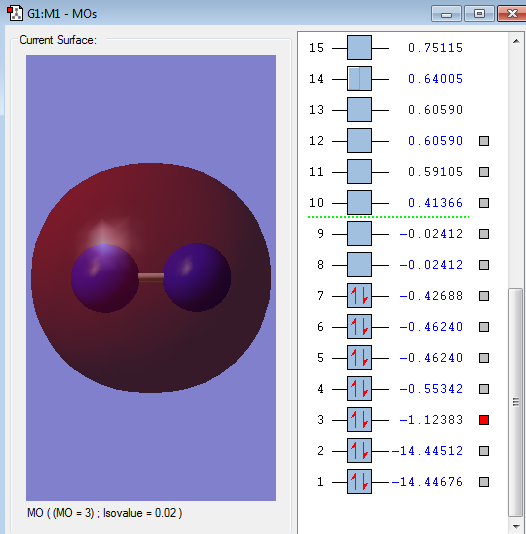
Type of orbital: 2s-2s bonding orbital
Energy of orbital:-1.12383 a.u.
Description: This is a bonding orbital that contributes strongly to the formation of chemical bonding. From the diagram, the 2s-2s MO is a extended circular surface that shows the big overlap.
Type of orbital: 2s-2s anti-bonding orbital
Energy of orbital:-0.55342 a.u.
Description: This is anti-bonding orbital has a relatively big energy difference with 2s-2s bonding orbital which can also indicate the better overlap of 2s-2s bonding orbital.
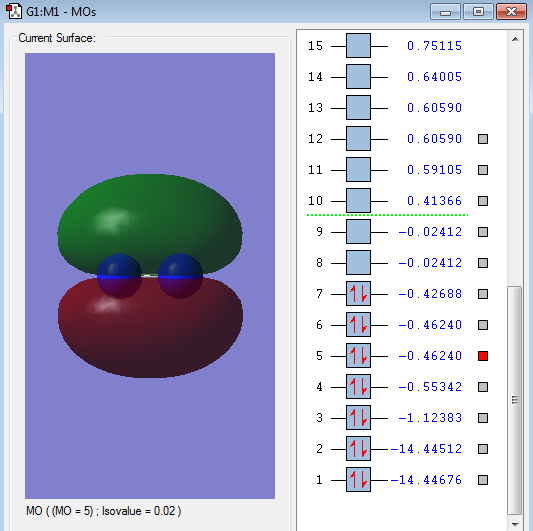
Type of orbital: 2p-2p bonding π orbital
Energy of orbital:-0.46240 a.u.
Description: This is a pi bond which formed from the side to side overlap of 2p AOs. There are 2 pi orbital with same energy. Since the existence of 3 x 2p orbitals, two of them are perpendicular to each other resulting in the formation of 2 pi bonds.
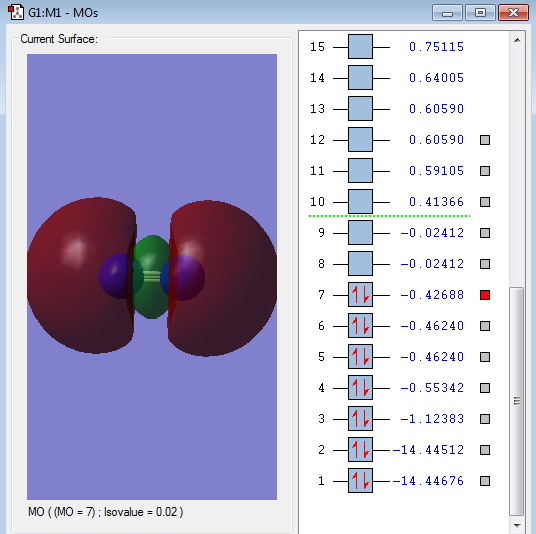
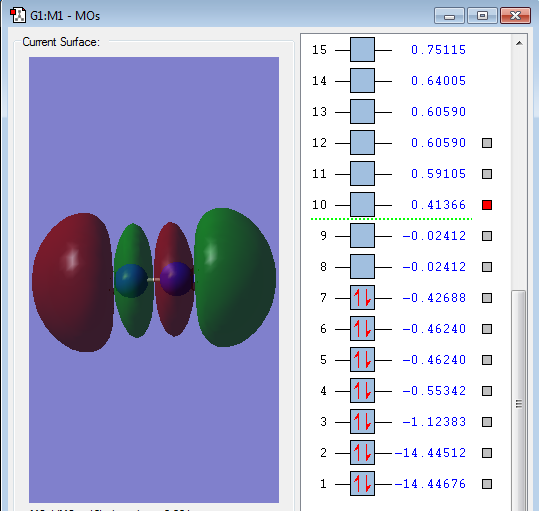
Type of orbital: 2p-2p bonding σ orbital
Energy of orbital:-0.42688 a.u.
Description: This is a sigma bonding that formed by the back to back overlap of 2p-2p orbital. Normally, the Sigma orbital should have a lower energy than pi bonding;however, the s-p mixing create a pi orbital with lower energy. [5]
Type of orbital: 2p-2p anti-bonding π orbital
Energy of orbital:-0.02412 a.u.
Description:This is an anti-bonding orbital which is unoccupied by electrons. The energy is quiet high that will destabilise the bond formation. However, there are no electrons in this orbital, so the chemical bond formed is not destabilized by this anti-bonding orbital
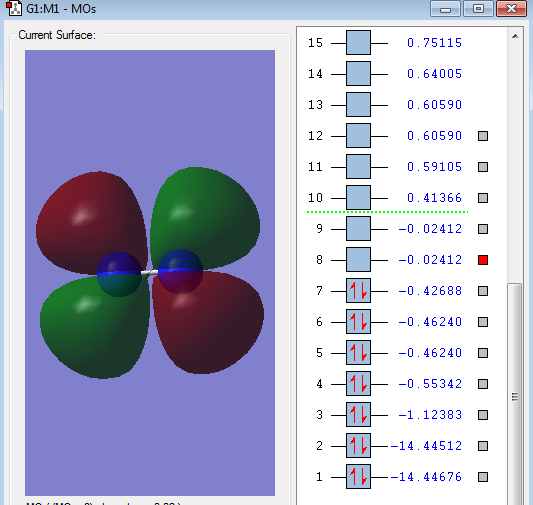
Type of orbital: 2p-2p anti-bonding σ* orbital
Energy of orbital:0.41366 a.u.
Description: This is the anti-bonding orbital with positive energy. But it also do not contain any electrons, so this orbital will not destabilize the chemical bond.
Haber-Bosch process
Reaction equation
N2 + 3H2 -> 2NH3
This reaction was used as the major production source of fertilizer. Originally, most of the plants can only obtain the NH3 under the help of thunderstorm, but with the fertilizer, they can absorb NH3 easily, thus they can grow more quicker and stronger. The N- atom is the essential components in amino acid, thus, more N- atoms, more amino acid and more protein in the plants. Since it is an exothermic reaction, the optimized temperature used is 450 degrees with 100 a.t.m. pressures. The catalyst is Iron. Based on these conditions, this reaction is relatively highly efficient for converting nitrogen gas and hydrogen gas into fertilizer.
Reaction energies
E(NH3)=-56.55776873 a.u.=-148492.421 kJ/mol
2*E(NH3)=-113.1155375 a.u.=-296984.843 kJ/mol
E(N2)=-109.52412868 a.u.=-287555.599 kJ/mol
E(H2)=-1.17853936 a.u.=-3094.255 kJ/mol
3*E(H2)=-3.53561808 a.u.=-9282.765 kJ/mol
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.5579074 a.u.= -146.48 kJ/mol
Since the reaction release energy which is exothermic reaction, the final product ( ammonia) is more stable than the gaseous reactants.
The literature value of reaction energies of Haber process is -45.7kJ/mol which much smaller than the calculated value. The difference may due to the different calculation method used. [6]
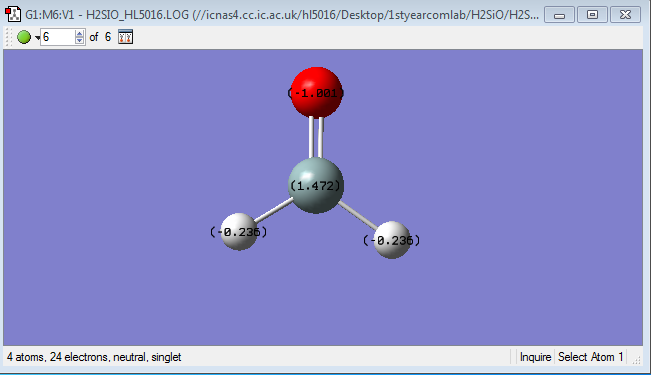
H2SiO
Basic properties of H2SiO
Calculation method:RB3LYP
Basis set:6-31G(d,p)
Final energy:-365.90001403 a.u.
RMS gradient:0.00000941 a.u.
Point group:Cs
Si-H distance:1.48652 Å
Si=O distance:1.53172 Å
H-Si=O Bond angle:124.15648 °
H-Si-H Bond angle:111.68594 °
Item Table of H2SiO
[here]
Item Value Threshold Converged?
Maximum Force 0.000023 0.000450 YES
RMS Force 0.000009 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000017 0.001200 YES
Predicted change in Energy=-5.109756D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4865 -DE/DX = 0.0 !
! R2 R(1,3) 1.4865 -DE/DX = 0.0 !
! R3 R(1,4) 1.5317 -DE/DX = 0.0 !
! A1 A(2,1,3) 111.686 -DE/DX = 0.0 !
! A2 A(2,1,4) 124.1565 -DE/DX = 0.0 !
! A3 A(3,1,4) 124.1576 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
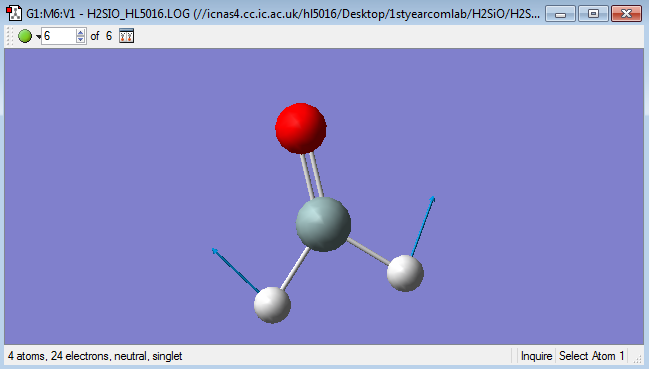
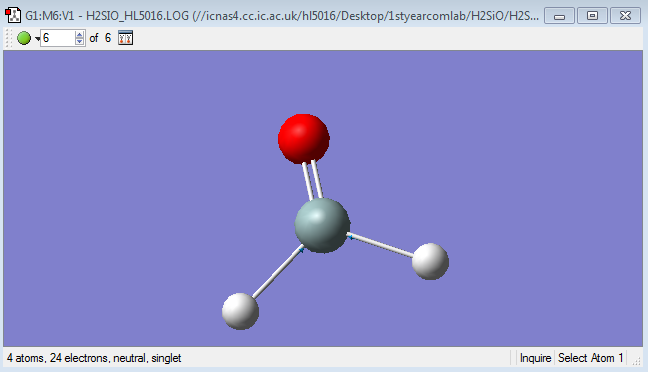
Diagram of H2SiO
H2SiO molecule |
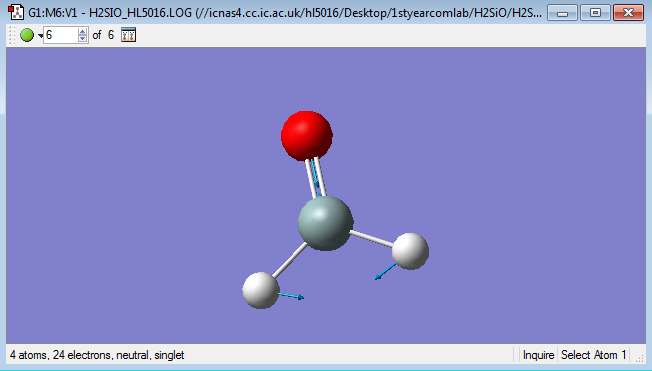
Vibrations
Mode of Vibrations
Vibration images
Mode 1
Frequency:698.63Hz
Intensity:58.6111
Type:Bending
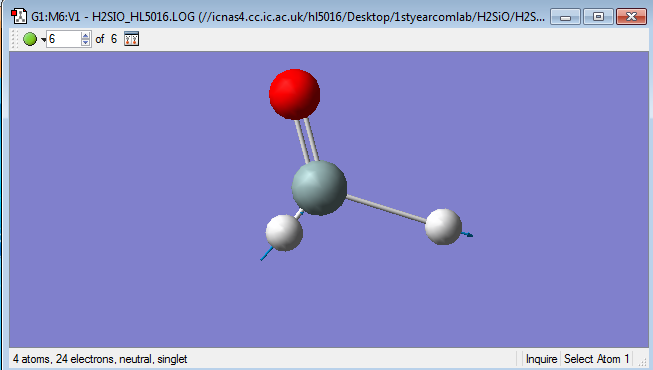
Mode 2
Frequency:712.10Hz
Intensity:61.2043
Type: Bending
Mode 3
Frequency:1037.98Hz
Intensity:55.3456
Type: Bending
Mode 4
Frequency:1219.23Hz
Intensity:64.9588
Type: stretching and bending
Mode 5
Frequency:2230.72Hz
Intensity:49.9752
Type: stretching
Mode 6
Frequency:2247.73Hz
Intensity:185.7008
Type: stretching
How many modes do you expect from the 3N-6 rule?
For the rule 3N-6, N represents the number of atoms which is 4 in H2SiO, So the expected number of modes should be 3*4-6=6.
Which modes are degenerate (ie have the same energy)?
None of the modes are degenerate since they do not absorb Infrad red with the same frequency.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Mode 1,2 and 3 are "bending" vibrations;Mode 5 and 6 are "bond stretch" vibrations.
Which mode is highly symmetric?
Mode 5 is highly symmetric.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
6 bands will be expected. But from the spectrum, only 4 bands were observed, since the value of frequency was quite similar, so they overlap to form a bigger band.
Charge Distribution
The charge on the Si-atom is +1.472;
The charge on the H-atom is -0.236.
The charge on the O-atom is -1.001.
Because O-atom has the biggest electronegativity value, so electrons are 'pulled' towards O-atom. For H-atom and Si-atom, H-atom has a bigger electronegativity than Si-atom, so H-atom is more negative charged since more electrons were pulled towards H-atom. The concept electronegativity is a chemical properties that means the ability to attract electrons towards itself.
MO orbitals
Coordinates
The Si=O bond is in z direction
The molecule is a trigonal planar structure and in z-y phase.
MO image:
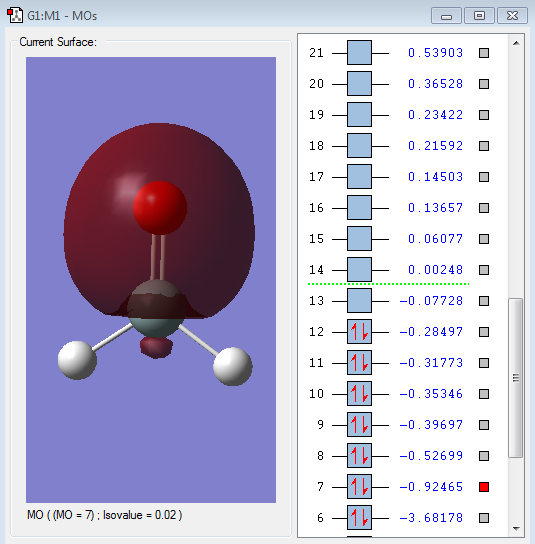
Type of orbital: 2s-2pz bonding orbital
Energy of orbital:-0.92465 a.u.
Description:This MO comes from the overlap of 2s orbital form o-atom and 2pz orbital from Si-atom. Since 2s orbital can only have one phase, but 2p orbital have 2 different phase, thus only part of the orbital will overlap. This MO orbital is occupied by electrons and will positively contribute to the chemical bond formation.
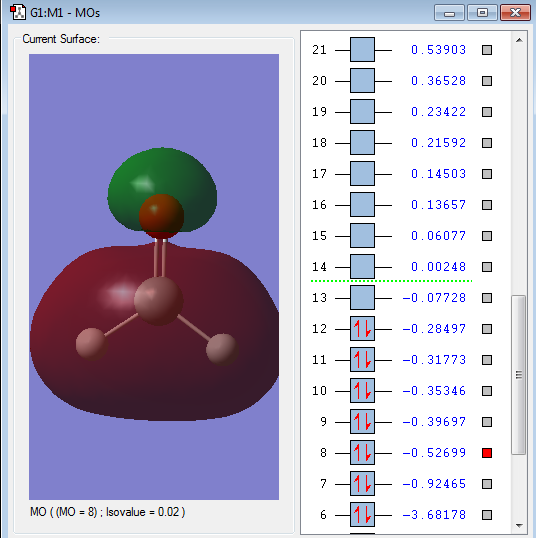
Type of orbital: 1s(H)-2s(Si)-1s(H) bonding orbital with a mixture of 2ps(Si)-2pz(H) anti-bonding orbital
Energy of orbital:-0.52699 a.u.
Description: This orbital is a mixture of bonding and anti-bonding orbital. The bonding orbital comes from the overlap of 1s(H)-2s(Si)-1s(H) AOs in the same phase, thus at the bottom the diagram, there is a big overlap area. The discontinuous of Si-O bond comes form the overlap of 2s(Si)-2pz(H) in the out-of-phase. Thus, there is no overlap orbitals between Si-O. This orbital is also occupied by electrons and will weaken the Si-O bond but strengthen the Si-H bond.
Type of orbital: 1s(H)(+)-2py(Si)(+)-2py(O)(+) bonding orbital
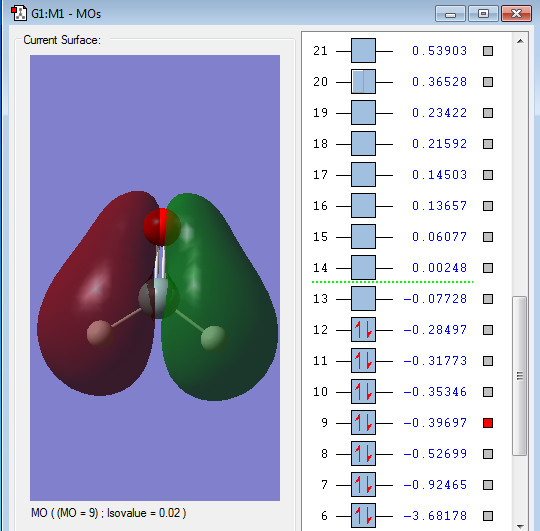
Energy of orbital:-0.39697 a.u.
Description: This orbital comes from a big overlap of 1s(H)-2py(Si)-2py(O), since the 2py orbitals has different phase, the 1s orbital for left hand side should have a different phase with the right hand side. Meanwhile, the phase of s and p orbitals all should be the same phase for each of the side. This orbital is also occupied by electrons and will stabilize the chemical bond formation
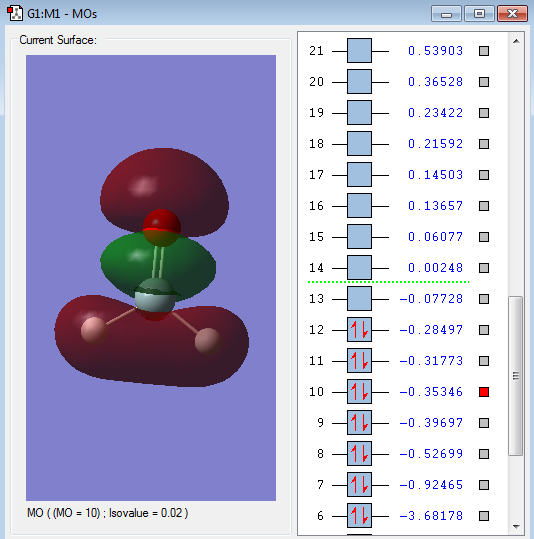
Type of orbital: 1s(H)-1s(H) bonding orbital and 2pz(Si)-2pz</sub(O) anti-bonding orbital and 2pz</sub(Si)-1s(H) anti-bonding orbitals
Energy of orbital:-0.35346 a.u.
Description: This orbitals is a mixture of bonding and anti-bonding orbitals. The 1s(H)-1s(H) overlap to form a bonding orbital but the 1s-1s system has a different phase with the 2pz</sub(Si), thus there is an overlap between Si and H atoms. The other anti-bonding orbital is the cancellation of the 2s(O)-2pz</sub(Si) AOs. The 2pz</sub orbital from O-atom also has a different phase with the 2pz</sub(Si), thus the 2pz</sub orbital from O-atom cancel with 2pz</sub orbital from Si-atom to create the discontinuities. Since the 2pz</sub(Si) orbital was cancelled by the s orbital from upwards and downwards, it become smaller. This orbital is occupied by electrons and will partially destabilize the bond formation.
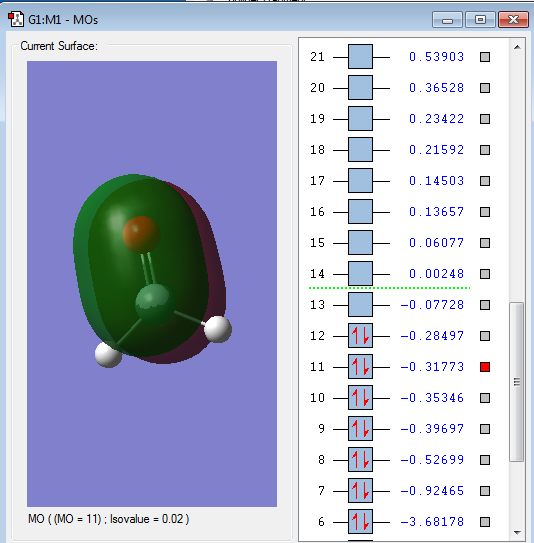
Type of orbital: 2px-2px bonding π orbital
Energy of orbital:-0.31773 a.u.
Description: This a pi bond which formed from the side to side overlap of 2px AOs. Since the 2 x 2px are perpendicular to 2pz resulting in formation of pi bond. This orbital is occupied by electrons and will stabilize the bond formation.
Reaction energies
E(H2SiO)=-365.90001403 a.u.
E(O2)=-150.25742434 a.u.
0.5*(O2)=-75.12871217 a.u.
E(H2)=-1.17853936 a.u.
2*E(H2)=-2.35707872
2*ΔE= 2*E(H2SiO)-[(O2)+2*E(H2)]=-579.185525 a.u.
ΔE=-289.5927625 a.u. = -7.60*105 kJ/mol
Reference
- ↑ Revore, M., & Mccarthy, M. I. (1996). Surfaces. Molecules, 3654(95), 7610–7616.
- ↑ Revore, M., & Mccarthy, M. I. (1996). Surfaces. Molecules, 3654(95), 7610–7616.
- ↑ Liang, T., Devine, B., Phillpot, S. R., & Sinnott, S. B. (2012). Variable charge reactive potential for hydrocarbons to simulate organic-copper interactions. Journal of Physical Chemistry A, 116(30), 7976–7991. doi:10.1021/jp212083t
- ↑ Mo, D., Bond, P., & Bond, D. (n.d.). MO Diagram for CO.
- ↑ MO theory for diatomic molecules. (2012).
- ↑ Modak, J. M. (2002). Haber Process for Ammonia Synthesis Jayant M Modak. Resonance, 7(8), 69–77.