Rep:Mod:14willh

Transition Structures and Reactivity

In this computational study, Gaussview 5.0, Gaussian installed on departmental computers and Gaussian 1px using the Imperial College High Performance Computing portal were all used.

Computational Methods

General

Gaussview provides a UI in which molecules and fragments to be studied are built or viewed by converting relative atomic positions into a set of cartesian coordinates. These coordinates can then be used to generate input files for performing various optimisation/ energy calculations using Gaussian (or many other commercially available packages eg. Spartan). Since molecules contain many nuclei and electrons, exact calculations are impossible for molecules larger than trivial H₂⁺, which means approximations are needed to simplify the calculations. This is done using a variety of methods. The method of choice determines the Hamiltonian used to solve the Schrödinger equation and the basis set describes how the total wavefunction is built.

Hartree-Fock Method

Hartree-Fock theory is considered as one of the most important ways to tackle nontrivial quantum mechanical calculations and is the basis of MO theory. It assumes that electrons can be described by time-averaged single electron wave functions (spin orbitals) on the premise that electronic and nuclear motion can be separated and electrons don't interact with each other. This means that the total wavefunction is a product of the orbital wave functions, known as the Hartee Product.

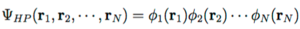
A fundamental postulate of quantum mechanics states that identical particles must be indistinguishable from one another, which means the Hartree product can be rewritten with exchange of electrons. Since the probability of finding each electron at a fixed nucleus is the same, at most, the total wavefucntion from the Hartree product can change sign (antisymmetric). To satisfy the antisymmetry principle, wave functions can be written in the following form:

For N electrons, this can be rewritten as a determinant, where each row represents each of the nuclear positions and each column is for the different orbital wavefucntions of each electron. This is called the slater determinant:

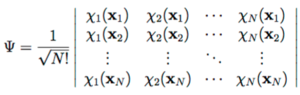
Determinants are used frequently in computational calculations since they reduce calculations to linear algebra, solved iteratively using diagonalisation. This provides the expanded LCAO basis set for the wavefunction. For the Hamiltonian, the full Hartree-Fock equations are given by:

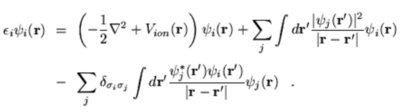
Since the theory discussed neglects interactions between electrons (electron correlation) and only takes an average potential from the other electrons (mean field), larger and more complex systems can lead to a poor descriptions where electron interactions may become important. For this reason, the HF method should not be used for accurate measurements of thermodynamic properties to compare with experiment, but rather can provide a fast and simple method for calculating relative properties and trends from which higher levels of theory can subsequently be carried out as required.

It should be noted that if more than one electron occupies the same spatial orbital (e.g. in a two electron system) their contributions cancel out meaning the function would be equal to zero. This is consistent with the well known Pauli Exclusion Principle.

DFT

Walter Kohn, Nobel Prize winner 1998 for the development of DFT.

If a larger structure is to be studied, for which the HF method would be too computationally tasking and expensive,(eg. in the calculation of the structure of DNA) density functional theorem is usually the first stop. DFT differs from HF in the fact that it uses electron density to calculate structures and properties, not a many-electron wavefunction as was discussed for HF. Although at first it was considered to be an inaccurate quantum mechanical method, refinement of approximations has made it a more promising technique in computational studies.

The most notable contribution to DFT was from Hohenberg and Kohn who developed the Hohenberg-Kohn-(Sham) theorems:

1. The electron density determines the external potential (to within an additive constant). This means many particle ground state energy of a molecule is a unique functional (function of a function) of electron density.(Proof)
2. The second theorem establishes a variational principle; For any positive definite trial density, ρt, such that ∫ρt (r)dr = N then E[ρt ]≥ E0

For an N-particle problem, there are 3N degrees of freedom (cartesian coordinates for each particle). By considering the electron density as approximately a single particle, the number of degrees of freedom - and hence the number of variables to calculate for - is reduced to just 3. This is clearly a huge simplification from solving the Schrödinger equation with 3N degrees of freedom and so the advantage of using DFT over HF is already evident. Where HF will quickly chew through computer power, DFT effectively only needs to solve for a single-electron-type wavefucntion. Subsequently, this means that individual energy terms can all be expressed as functionals of the equilibrium charge density. Another advantage of DFT over HF is that it includes kinetic energy and exchange-correlation energy (potential due to spin and charge) in the expression for the total energy of the system. Although with complete basis of single-electron wavefunctions the HF method is best since it will be the closest approximation to the exact solution, for many electron molecules (i.e. pretty much every molecule since a basis set completely defined by single electron wavefunctions only happens for the smallest of molecules) DFT is able to calculate values fairly accurately (with the inclusion of KE and correlation energy) without the need for expensive, high performance computers and with the inclusion of electron correlation.

For an in-depth introductory discussion of DFT by Harrison, Imperial College Chemistry Department, click here.

Since both methods adopt different basis sets, it is trivial to compare energy results.

Optimisation Processes

Introduction

The method and basis set chosen defines the shape of the potential energy surface (PES) for a molecule. Methods using the B-O approximation give the total energy in terms of nuclei-nuclei interaction and the electronic energy with respect to nuclear coordinates. Stationary points, where the gradient is zero, on the PES correspond to reactants, products and transition structures.

These points are given by the differential of the PES. From physics it is known that the differential of energy gives the negative force (F=-dE(R)/dR). Hence, the gradient of the PES will give the force acting on the particles at the specified coordinates. So at the reaction minima, the geometry is optimised because the total forces acting upon the molecule are equal to zero. The second derivative of the PES gives the force constant. The force constant for every atom with a molecule at given coordinates is called the Hessian (force constant matrix) where each individual force constant that makes up the Hessian is an eigenvalue of the Hessian.

The Hessian gives information on the curvature of the PES and some optimisations (Newton-Raphson) use this to find the closest stationary point. When all eigenvalues of the Hessian are positive (upwards curvature in every direction) the point is a minimum; when all eigen values are negative the point is a maximum; when the eigenvalues are both negative and positive the point is a saddle point of an order given by the number of negative eigenvalues. For a TS, the saddle point is first order (ie. only one negative eigenvalue).

Many optimisation algorithms use the fact that the expression for the PES can be rewritten as a Taylor series. Then, using a quadratic approximation (ie. only expanding to the term of order 2 (third term) to be significant), the PES energy about a point can be written as, where g is the positive gradient, H is the Hessian and x is the step from x₀:

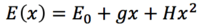
The gradient is zero at a stationary point, hence, where x_i is the Newton-Raphson (NR) step and h is a Hessian eigenvalue:

Another optimisation method that builds on the ideas of NR is the rational function optimisation (RFO), which is used in Gaussian. Whereas NR will locate the nearest local stationary point (regardless of its nature), which is not helpful for exploring other parts of the PES, the RFO method uses a shift parameter so that:

The optimisation then computes a linear search between the latest and best previous point by branching off previous paths and exploring stationary points that may not be the local minima. The two methods can be represented pictorially as:

Gaussian

With all of the above in mind, once the method and basis set has been chosen, Gaussian optimises the geometry in the following way:

• Gaussian optimises information on the given PES using a Berny algorithm with rational function optimisation (RFO) and convergence criteria using a list of redundant internal coordinates (bond lengths, angles and dihedrals).
• The initial Hessian is the calculated numerically by 'diagonalising the Hessian'. Calculating the Hessian after every step is time consuming and so is only updated at predetermined intervals or when close to minima using updating schemes:

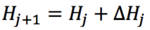
• The steps in-between these steps update the Hessian by approximations using the computed energies and gradients of the last set of coordinates.
• After the optimisation of each step, the following table is outputted:

Item               Value     Threshold  Converged?
 Maximum Force            0.022366     0.000450     NO 
 RMS     Force            0.005364     0.000300     NO 
 Maximum Displacement     0.136975     0.001800     NO 
 RMS     Displacement     0.038308     0.001200     NO 
 Predicted change in Energy=-2.222789D-03

• RMS is the root mean squared value from all of the atoms. The process is repeated until all values are below the threshold convergence criteria. The optimisation is said to have converged and the optimum geometry is found (although the energy will always be slightly higher than the real minima).
• Combinatorial Explosion Problem: The number of local minima typically goes exponentially with the number of variables (degrees of freedom).

The Cope Rearrangement

Cope Rearrangement of 1,5-hexadiene through three theoretical transition structures. At this time, the path highlighted involving the aromatic transition structure is considered to be the one that is followed after extensive computational studies since the initial discovery of the Cope rearrangement.

Chair and Boat conformations of the the aromatic transition state, which closely resemble cyclohexane.

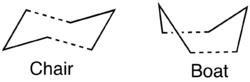
Introduction

The Cope rearrangement , first reported over 70 years ago, is a well known [3,3]-sigmatropic rearrangement reaction in which two π bonds and one σ bond are broken and then reformed to give a more thermodynamically stable regio-isomeric product. Much research has been conducted since then to probe the mechanistic features of the reaction and to understand its high degree of regio- and stereo- selectivity. Organic texts discuss such reactions extensively and often explain the control of the reaction in terms of orbital interactions (e.g. Woodward Hoffmann rules). However, transition-state geometry is the key to understanding the control in these types of reactions and formulating bench-top rules for these tendencies.

The original representation of the reaction mechanism depicted a concerted mechanism for bond migration with an aromatic transition state (TS), however there was debate for many years with supporting evidence for a bis-allyl or 1,4-diyl TS and there was also discussion on the energy differences of the chair and boat conformations. Since TSs are transient species, they cannot be viewed in the regular spectroscopic ways (they have a very short half-life) and so much of the arguments for each TS was based on computational modelling results and comparisons of thermodynamic and physical data, often using kinetic isotope effects (KIE), to experimental values to validate results. The development of computational modelling was occurring at the same time as much of this debate and so the Cope rearrangement is heavily intertwined within this

The difficulty in modelling the Cope rearrangement arises from the flatness of the potential surface close to local-minima. In the 90s, Wiest et al. conducted a study of a handful of different computational methods as applied to the Cope rearrangement using density functional theory (DFT), from which it was determined that the B-LYP and Becke3-LYP methods provided estimates of reaction activation energies that were as close as 1 kcal/ mol to experimental values using the 6-31G* and 6-311+G** basis sets.

Aims

In this tutorial:

• Optimise the geometries of the reactants/ products of different 1,5-hexadiene conformers to locate their low-energy minima and the overall global minimum energy structure on the potential energy surface, to determine the preferred reaction mechanism.
• Symmetrise optimised structures to find their point group
• Calculate and visualise vibrational frequencies
• Correct Potential energies in order for them to be comparable with experimental data.
• Optimise the - cyclohexane like - chair and boat TS conformers. The lowest energy TS will be the most stable and will proceed to form the kinetic product.

Optimising the Reactants and Products

In this discussion, the reactants and products of the rearrangement of different 1,5-hexadiene conformers are optimised using the HF/3-21G level and the higher B3LYP/6-31G* level of theory, where. Thermodynamic, physical and conformational data is compared to experiment and intuition.

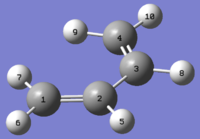
1,5-hexadiene has 10 energetically distinct conformations due to free rotation about 3 C-C bonds, all of which have been calculated at the HF/3-21G and B3LYP/6-31G* levels of theory as presented in the table below. The conformations were built based upon the Newman projections, adjusting dihedral angles accordingly and then cleaned using the Clean function. Each conformation retained its symmetry following the optimisation process, which indicates that the initial guess conformations, using Newman projections, are reasonable first estimates of the final structures. The table of conformations is shown below, where the structures shown are from the HF/3-21G level of theory.

The calculated energies are expected to be negative; this is because Gaussian sets the energy to zero for when atoms that make up the molecule are infinitely far apart (don't interact). As the atoms are brought together, bonding interactions are formed, which are stabilising/ energy lowering interactions. So, overall, the formed molecule will have an energy less than zero.

Click on the energy data for DOI files. Units were converted from Hartrees to kcal/mol using the online Energy Units Converter from Colby College chemistry department. Energies are relative to the lowest calculated energy conformer.

Conformer	Structure	Point Group	Energy/ Hartrees HF/3-21G	Relative Energy (HF method)/ kcal/mol	Energy/ Hartrees B3LYP/6-31G*	Relative Energy (DFT method)/ kcal/mol	Central C3-C4 Bond Length/ Å
gauche1	Jmol	C2	-231.68771610	3.1031103129	-234.60786363	2.4703421743	1.53935
gauche2	Jmol	C2	-231.69166694	0.62392025307	-234.61070757	0.6857424997	1.55071
guache3	Jmol	C1	-231.69266122	0	-234.61132934	0.29557585067	1.55322
gauche4	Jmol	C2	-231.69153035	0.70963179043	-234.61048196	0.82731494232	1.55533
gauche5	Jmol	C1	-231.68961570	1.9110930614	-234.60911048	1.6879318195	1.54569
gauche6	Jmol	C1	-231.68916020	2.1969236879	-234.60888834	1.8273268039	1.54314
anti1	Jmol	C2	-231.69260235	0.03694149062	-234.61180037	0	1.55231
anti2	Jmol	Ci	-231.69253506	0.079166612149	-234.61170282	0.061213562263	1.55305
anti3	Jmol	C2h	-231.68906680	2.2555330853	-234.60752006	2.6859356503	1.53477
anti4	Jmol	C1	-231.69097053	1.0609242192	-234.61078874	0.63480754477	1.54363

Optimisation of the Anti1 Conformer (approx. anti-periplanar)

Using the Newman projection in the table above as a guideline, the anti1 conformer was built approximately and then the dihedral angle of the central C-C bond was changed to 180º. After cleaning the structure using the Clean function, a note of the initial point group was made and then optimisation of the structure was carried out at the HF/3-21G level. The structure was optimised in around 10 seconds (owing to a small basis set). The output data is recorded in the table above and is consistent with the data provided in the tutorial Appendix 1.

Anti1 Conformer

Optimisation of the Gauche1 Conformer

Using the Newman projection in the table above as a guideline again, the gauche conformer was built approximately and then the dihedral angle of the central C-C bond was changed to 0º. After cleaning the structure using the Clean function, a note of the initial point group was made and then optimisation of the structure was carried out at the HF/3-21G level. The structure was optimised quickly as for the anti1 conformer (owing to a small basis set as discussed) and again the output data in the table above is consistent with what is given in the tutorial Appendix 1.

Gauche1 Conformer

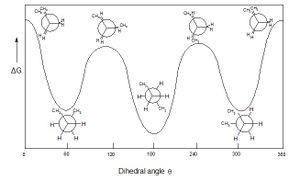
Normally, it is expected, from conformational analysis using Newman projections, that anti conformations are lower in energy than than gauche conformations. This is due to destabilising interactions and torsional strain in the gauche conformation, which is relieved in anti conformations:

Typical trend of conformer energy as a function of dihedral angle, θ, using butane as an example.

This means that the gauche1 conformer would be expected to have a higher energy than the anti1 conformer. Indeed, the optimisations at the HF/3-21G level calculate the gauche1 conformer to be higher in energy than the anti1 conformation. To further justify this, it is good practice to inspect molecular orbitals:

Gauche1 HOMO

Anti1 HOMO

It is clear from the HOMOs for the anti1 conformer that there is a small amount of extended delocalisation, namely hyper conjugation, that extends to hydrogens adjacent to the double bonds. This extra stabilisation is not seen for the gauche1 conformer, and so anti1 will be lower in energy (as predicted using Newman projections). Also, for the gauche1 conformer, the two double bond terminal ends of the molecule are much closer together than for the anti conformer; this will increase the energy of the gauche1 conformer. Combining these effects, running in opposite directions, helps explain the large energy gap between the anti1 and gauche1 conformers.

Optimisation of the Gauche3 Conformer

From the table above, it is evident that the gauche3 conformer has the lowest energy structure at the HF/3-21G level. It is important to optimise a range of conformers to find the global minimum as it is not always obvious which structure will be the lowest. This is evident here where we would normally expect gauche conformers to be higher in energy than the anti conformer, but the HF/3-21G level of theory has calculated it to be the other way around. Again, to further investigate this, the molecular orbitals are inspected:

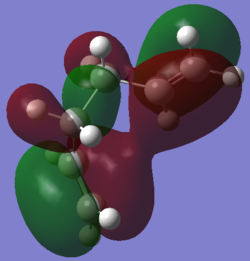
Gauche3 HOMO

Anti1 HOMO

This is the HOMO for the gauche 3 conformer. It shows that the occupied orbitals have a slightly delocalised π-electron cloud, which can not be seen in the HOMO for the anti1 conformer. This extra stabilisation from the delocalisation is larger than the destabilisation from being in a gauche conformer and so the total effect is that the gauche3 conformer is lower in energy. The delocalisation is only slight, though, and so it would be expected that the energy will not be much lower than the anti1 conformer. This is seen from the calculated energies, which show a very small energy gap between the two conformers especially since the anti1 conformer does have a bit of extra stabilisation as discussed above.

Although this discussion is true at the HF/3-21H level, the table of data above shows a different order of relative energies for the B3LYP/6-31G* level. At this level of theory, calculations predict the same three lowest energy conformers (gauche 3, anti1, anti1), but using the larger basis set shows the order to be anti1<anti2<gauche3 from largest to smallest with anti1 and anti2 being very close in energy and gauche3 not so close. The orbital argument above can still be used to explain why gauche 3 is lower in energy than the anti3 and anti4 conformers since orbital inspection shows that there is almost, but no delocalisation between π-systems. At this level of theory there steric interactions have been calculated to be much more favourable and orbital inspection shows that the hyper conjugation of the HOMO is much larger than calculated at the HF/3-21G level. Therefore, the anti1 and anti2 conformers are lower in energy. This occurs at the higher level of theory because DFT takes into account electron correlation (electron interactions) and does not take a mean field, so it is better able to calculate the stereoelectronic interactions more accurately.

Optimisation of the Anti2 Conformer at the HF/3-21G and B3LYP/6-31G* Levels

The output data is recorded in the table above and is consistent with the data provided in the tutorial Appendix 1. After both optimisations had been carried out, on first inspection it didn't look like the higher level of theory had changed the geometry much if at all and both still had C_i symmetry. As discussed in the computational methods section, HF will provide a very good approximation, but does not account for exchange correlation and only treats the electronic interactions as a mean field, which is over estimated. It was also said that DFT must be used for large basis sets or if electronic interactions become important. In the case we are considering, we have already seen how important electronic interactions are in deciding which conformer is lowest in energy and so structures should be reoptimised using DFT, which does account for exchange correlation. Using Gaussview, the geometry of the structures from both levels of theory were quantified by dihedral angles and bond lengths.

Bond Lengths

Labelling of the Anti2 Conformer

HF/3-21G Bond	HF/3-21G Bond Length/ Å	B3LYP/6-31G* Bond	B3LYP/6-31G* Bond Length/ Å
C1-C2 (double)	1.31621	C1-C2 (double)	1.33351
C2-C3 (single)	1.50896	C2-C3 (single)	1.50409
C3-C4 (single)	1.55305	C3-C4 (single)	1.54807
C4-C5 (single)	1.50869	C4-C5 (single)	1.50409
C5-C6 (double)	1.31621	C5-C6 (double)	1.33351

The typical C=C bond length is around 1.34 Å. Comparing this with the data above, the calculated C=C bond lengths for both methods are lower this with the bond length at the HF/3-21G level of theory being the lowest. This could initially suggest that the HF method is not sufficient at accurately predicting the precise geometry of a molecule due to this relatively large difference. Also the DFT B3LYP method is using a more precise, 6-31G*, basis set than the HF method, which could be another reason for this difference. Using a more precise method is useful if results are to be compared to experimental physical/ thermodynamic properties. However, increasing the precision of the basis set and using a higher level of theory will quickly eat into computational power and will no longer be simple 'bench top' calculations that can be carried out on a regular PC. In this study, our molecule is small and so the basis set will still not be large, however for more complex molecules this is definitely a factor to consider.

Dihedral Angles

HF/3-21G Carbons	HF/3-21G Dihedral Angle/ Degrees	B3LYP/6-31G* Carbons	B3LYP/6-31G* Dihedral Angle/ Degrees
C1-C2-C3-C4	114.685	C1-C2-C3-C4	118.518
C2-C3-C4-C5	180.000	C2-C3-C4-C5	180.000
C3-C4-C5-C6	-114.685	C3-C4-C5-C6	-118.518

180º is seen for both levels of theory since we are looking at the anti periplanar conformer and so this angle will be fixed at 180º no matter what level of theory is used. This is also why corresponding angles differ in sign: the bonds are pointing in opposite directions. A sp² substituent bond angle is 120º. Again, we can see that the HF/3-21G level has predicted a value much lower than this whereas B3LYP/6-31G* is much closer to this. This is further evidence that the B3LYP/6-31G* level of theory is a more accurate method to use.
It is important to note that, although the angles and bond lengths change (and therefore the cartesian coordinates), the point group does not change upon changing the level of theory. This is because bond angles change by equal magnitude on both sides of the centre of inversion.

Zero-Point Energy Correction

As described in the tutorial script, the calculated energies of each conformer correspond to the energy of a molecule on a bare potential energy surface at 0K without accounting for zero-point energies for the vibrational contribution to energy. To be able to compare the calculated energy values to experiment, a zero-point energy correction needs to be carried out, which will derive absolute values that are comparable to experiment. This is done by carrying out a frequency analysis at the same level of theory on the structure under investigation. For the anti2 conformer, the frequency analysis was conducted using the B3LYP/6-31G* level and all of the frequencies were found to correspond to real vibrations thereby confirming that the structure is not a transition structure. Data Files.

The thermochemical zero-point correction data at 298.15K from this frequency analysis is shown below:

Zero-point correction=                           0.142492 (Hartree/Particle)
 Thermal correction to Energy=                    0.149849
 Thermal correction to Enthalpy=                  0.150793
 Thermal correction to Gibbs Free Energy=         0.110877
 Sum of electronic and zero-point Energies=           -234.469211
 Sum of electronic and thermal Energies=              -234.461854
 Sum of electronic and thermal Enthalpies=            -234.460910
 Sum of electronic and thermal Free Energies=         -234.500825

The sum of the electronic and zero-point energies correspond to 0K since at this temperature there are no contributions from rotational or translational energy. The sum of the electronic and thermal energies are taken at 298.15K and 1 atm (standard conditions) where now there will be contributions from the other energy forms and so explains why this energy is higher. The sum of the electronic and thermal enthalpies correct for enthalpy contributions at 298.15 K. Using H=E+RT at 0K, it can be seen that the RT=0 and therefore H(0)=E(0). As the temperature is further removed from 0K, the RT terms increases to a significant value and at 298.15K we would expect to see that the thermal enthalpy is higher than the calculated thermal energy. This is the case for the calculate data above. A similar consideration is applied to the sum of the electronic and thermal free energies: using G=H-TS, at 0K the entropy does not contribute (although residual entropies may need to be considered in some systems), but at 298.15 K the TS term is significant to visibly decrease the free energy below the thermal enthalpy. The TS term is also expected to grow at a much faster rate than RT and so the decrease in free energy will be greater than the increase in thermal energy. This explains why the sum of the electronic and thermal free energies at 298.15 K, 1 atm is lower than the thermal energies and enthalpies. Such entropy of of a system is determined using statistical thermodynamics and the molecular partition function:

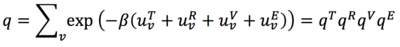
The thermochemical zero-point correction data at 0K was calculated by using the freqchk utility in Gaussian. The output, as expected, shows that all four energies are equal to the sum of electronic and zero-point energies from above. This shows that this quantity does not change with the temperature, again as expected:

Sum of electronic and zero-point Energies=           -234.469211
 Sum of electronic and thermal Energies=              -234.469211
 Sum of electronic and thermal Enthalpies=            -234.469211
 Sum of electronic and thermal Free Energies=        -234.469211

Optimising the "Chair" and "Boat" Transition Structures

Chair Transition Structure

It has already been described that the chair TS is lower in energy than the boat TS by analysing it as an analogue of cyclohexane. The chair conformer was built on Gaussview by first building an allyl fragment and optimising is at the HF/3-21G level. This fragment was then duplicated and the two fragments were rotated and translated so that they approximated a chair structure with a distance of approximately 2.2 Å between them. The Clean function was used to clean this structure and the point group was changed to C_2h using the Symmetrise function up and get something closer to the real chair structure.

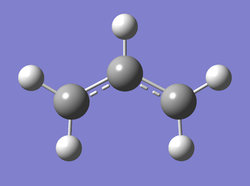
Allyl Fragment Data Files

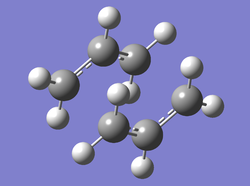
Chair TS Guess Geometry Input File

TS optimisations are more difficult than reactant/ product minimisations because the TS will be at a saddle point. At this saddle point, the TS is a minimum in one direction but a maximum in another direction. The reaction path proceeds via minimum energy (mep) so the calculation needs to know where the direction of negative curvature is since if the TS is a maximum energy structure then moving from the TS along the reaction coordinate will result in a lowering of the energy. The second differential of the PES is its curvature and relates to the force constant matrix (known as the Hessian). Taking the simple harmonic oscillator model for bond vibrations, the vibration of a bond is given by:

Harmonic Oscillator Frequency Equation

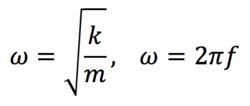
Where w is the bond vibration angular frequency, k is the bond force constant.The frequency from the expression above is proportional to the square root of the force constant. For a minimum energy reactant/ intermediate/ product, the PES will have a positive curvature moving in any direction from this point, which means they will have vibrations all with positive force constants (real frequencies). A TS, on the other hand, (which will have negative curvature either side of the reaction coordinate) will result in a negative k. The square root of a negative number does not belong to the set of real numbers (imaginary). This means that if we have a single imaginary frequency after a frequency calculation, then the structure is a possible TS. However, like for the reactants and product conformers, there may be more than one possible TS structure and it is important to optimise all of them to find the global minimum (the one through which the reaction will proceed under non-photochemical conditions).

Optimisation: Eigenvector Following

This first method of optimisation assumes that the initial guess at the TS is close to the final calculated structure. The gaussian calculation of the guess chair structure was set up with Opt+Freq selected; Optimisation to a Minimum changed to Optimisation to a TS (Berny); calculate force constants Once; and the additional keywords Opt=NoEigen were added. The additional key words stops the calculation from crashing if more than one imaginary frequency is found during the optimisation. This occurs if the initial guess structure is far form a TS, hence should not be used unless a reasonable guess structure is already known. Frequency analysis of the optimisation output (output data found here) shows a single imaginary frequency at -817.89 cm^-1. This vibration corresponds to the transition vibration in the Cope rearrangement and is shown below. Data Files

Optimisation: Frozen Coordinate Method

The second method of optimisation is useful if a reasonable guess of the tradition structure cannot be made, which is useful for probing new reactions where mechanisms have not been studied in detail and for larger molecules where more complex TS would be hard to guess. Using the pre-optimisation guess structure again, the interactions between terminal carbons of the allyl fragments were frozen using the Redundant Coord Editor with the bond lengths being fixed to 2.2 Å. The optimisation was simply set up at the HF/3-21G level with the Job Type set to Optimisation as for a minimum energy geometry. The input line should show Opt=ModRedundant. The output was symmetrised to a C_2h point group and the structure was optimised as a minimum again. Data Files

The redundant coordinates were now set to Bond and Derivative so that the numerical Hessian of the redundant bonds are now calculated and optimised. The optimisation was set up for a TS as before (Opt+Freq TS (Berny) Opt=NoEigen), but with the force constant calculation set to Never so that the optimisation doesn't calculate a completely new Hessian, but adjusts the Hessian based on the new information given by the optimisation of the previously frozen coordinates. The output structure is shown below with a single imaginary frequency at -817.76 cm^-1, which is comparable the that found using the previous method giving an initial indication that the two methods lead to the same transition structure. Data Files

Comparison of Optimisation Methods

As discussed above, the first method is best used for when the guess transition structure is well known and close to the actual TS structure. However, if this is not known then the frozen coordinate method should be used. To make sure that both optimisations lead to the same structure a bond length analysis was carried out. The forming and breaking bond lengths were found by visualising the vibrations and setting Manual Displacement to a maximum; saving the structure; and then inspecting the distances between the terminal carbons.

Method	Forming Bond Length/ Å	Breaking Bond Length/ Å	Intermediate Bond Length/ Å
Eigenvector Following	1.16523	2.88481	2.02137
Frozen Coordinate	1.16416	2.88411	2.02073

From this it is seen that there is only a difference of 0.001 Å (3.d.p) between the methods for forming and breaking bond lengths. The intermediate bond length shows that both methods are correct to 3.d.p. So overall it can be said that there is no real difference between the calculated structures, which is backed up further with similar imaginary frequencies (-817.89 cf. -817.76 cm^-1).

Boat Transition Structure

As discussed above, we need to optimise all of the guess transition structures to make sure that we find the global minimum. Although by analysing the chair and boat transition structures as for cyclohexane we expect the boat TS to be higher in energy due to van der Waals strain from "flagpole" interactions, the boat TS should be optimised for structures with substituents as there may be favourable interactions which are not noticeable at first glance (like for the gauche3 conformer being lower in energy than the anti1 conformer).

Optimisation: QST2 Method

QST2 stands for quadratic synchronous transit. It locates the TS by interpolating along the PES parabola that connects the reactants and products guided by quasi-Newtonian mechanics to find the TS that would be needed. If the interpolation is carried out linearly between the reactant and product structures, the method is called linear synchronous transit (LST). The initial guess is a structure exactly between the reactants and products. QST2 works well for reactions where the reactant and product structures can be specified (eg. bimolecular reactions), but gives poor guess structures for isomerisaiton reactions due to poor interpolation. A more robust method that does not fail due to poor guess structures is QST3 since you are able to specify an initial guess structure unlike for QST2, which only needs reactants and products to be specified.
QST methods do not require a full evaluation of the Hessian, unlike the eigenvector following methods, which means methods such as CCSD(T) can be used where analytical Hessians are not available.

The numbering of the reactants and products was manually changed to ensure that it was consistent with rearrangement. The reactant and products were numbered as follows using the optimised anti2 reactant molecule previously calculated:

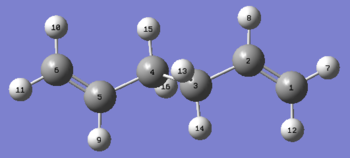
Reactant

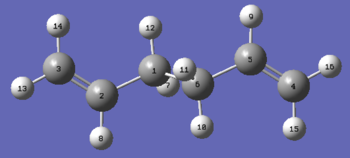
Product

This was then optimised to a transition state as before (Opt+Freq, Once, Opt=NoEigen), but to TS(QST2) instead of TS(Berny). The result of the calculation is shown below. Clearly this is not the right TS since it is more chair-like than boat and the bonds being formed/ broken are not consistent with the Cope rearrangement. This failure is because when the calculation was being carried out, the method only translated allyl fragments and did not interpolate using structures rotated about bonds. Again this is an indication that QST2 does not work if the initial guess structure is not good enough due to poor interpolation discussed above.

QST2 Failed Optimisation
Data Files

To resolve this, the angles of the reactant and product in the input file were modified so that their geometries are closer to a boat transition structure. For both the reactant and product, the C2-C3-C4-C5/C2-C1-C6-C5 dihedral angles was changed to 0º; C2-C3-C4/C2-C1-C6 and C3-C4-C5/C1-C6-C5 angles were changed to 100º. This gives the reactant and product molecules shown below:

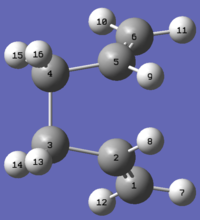
Reactant

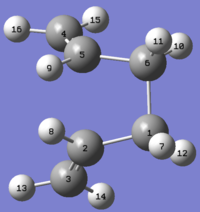
Product

The calculation was set up in the same way as before, which converged to a boat TS with a single imaginary frequency at -838.14 cm^-1 as shown below (Data Files):

QST2 Boat TS After Modifying Angles

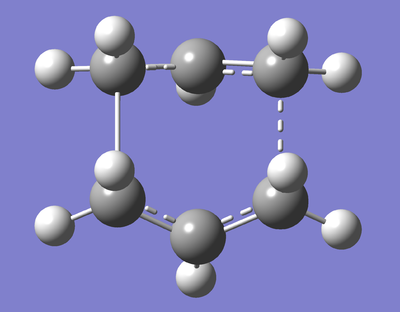
Optimisation: QST3 Method

As discussed previously, the QST2 method may lead to poor interpolation. To overcome this, the QST3 method could be used, which requires a manual input for the guess structure of the transition state. This is a much more robust method if a reasonable guess structure can be made. The reactant and product geometries and labelling are the same as for the QST2 method. The guess structure now for the QST3 method is shown below with appropriate labelling:

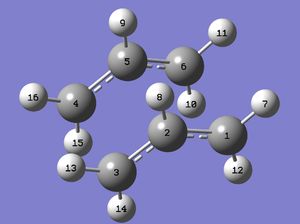
Guess Boat TS

This optimisation converged to a boat TS without the need to modify reactant or product angles and a single imaginary frequency was found at -840.01 cm^-1, which is very similar to that found from the modified QST2 method. This shows that, although QST2 is fully automated, QST3 is more robust in that the initial interpolation is closer to the final TS and so modification of input reactants and products is not required (Data Files)

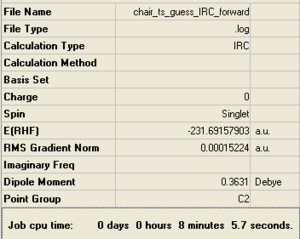
Intrinsic Reaction Coordinate (IRC)

IRC Results after 50 Steps

It is difficult to predict which conformer will form the transition state by just looking at the TS and so IRC is used to connect the reactants and products to the TS. IRC is a special case of the minimum energy path (MEP) and is useful as it enables visualisation of possible intermediates that may not have been thought about previously as well as connecting the whole reaction together.

The basic idea of IRC is to take small steps in mass-weighted coordinates from the TS to the local minimum of the reactants or products. This is done moving along the path for with the second derivative of the PES is most negative (highest curvature) taken at each of the points with a predetermined step length and terminates when energy minima are reached (reactants/products). This method is powerful in that it provides the hight of the reaction barrier, thermodynamic properties and reaction rates.
The IRC for this reaction was calculated using the chair TS from the eigenvector following method. IRC was selected as the Job Type; compute the forward reaction coordinate (since in this case the product and reactants are the same energy and so the reaction will be symmetrical about the TS); calculate the force constant Always; N=50 Steps.

After 44 steps, the IRC had found a minimum and stopped the calculation, however the final structure did not correspond to one of the minimum energy 1,5-hexadiene conformers with a final energy of -231.69157903 a.u.. However the structure did look a lot like the gauche2 conformer, which gave an initial indication of a kinetic product or even a reaction intermediate. This geometry and the IRC/path is shown below.(Data Files)

The RMS is the root mean squared force on the structure which is equal to the gradient at a point on the PES. At stationary points, the gradient is zero and hence the RMS will be zero which is why the RMS starts at zero (from the TS) and converges to zero at higher reaction coordinates. The RMS (from reactants to TS) will increase exponentially as bonds become more strained with geometrical changes until it reaches a maximum. At this point, bonding interactions actually breakdown so as to relieve the strain, which is why the RMS then decreases sharply until the TS stationary point is reached and the RMS is zero again.

Point Number:  43          Path Number:   1
   CHANGE IN THE REACTION COORDINATE =    0.31433
   NET REACTION COORDINATE UP TO THIS POINT =   13.51239
  # OF POINTS ALONG THE PATH =  43
  # OF STEPS =   1

 PES minimum detected on this side of the pathway.
    Magnitude of the gradient =      0.0001432
 Calculation of FORWARD path complete.
 Reaction path calculation complete.

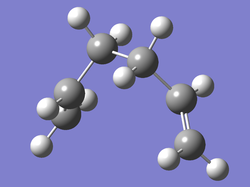
IRC: Gauche2-Like Geometry after 44 Steps

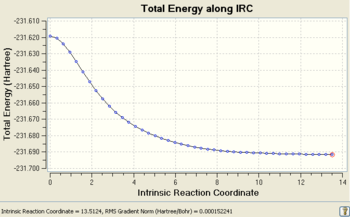
IRC: Energy Path After 44 Steps

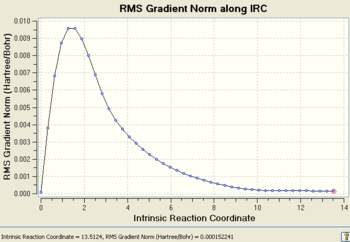
IRC: RMS Gradient Normal After 44 Steps

At this point there is three different things that can be done to reach the actual minimum:

Approach	Discussion
Run a minimisation from the last point on the IRC	This approach is the fastest, but minimisation may not give the global minimum rather a local minimum that does not correspond the the product geometry.
Restart the IRC with more steps	Can be a more reliable approach if the TS and products aren't too far from each other since using too many points can cause the IRC to veer off in the wrong direction.
Restart the IRC with computing the force constant at every step	This is the most reliable method, but very time consuming and requires a lot of computing power, which means that it is not feasible in larger macromolecular systems.

IRC: Minimisation From the Last Point on the IRC

The final structure from the first IRC calculation was copied and pasted to a new molecule group window. This structure was then optimised at the HF/3-21G level of theory. The final energy for this optimised structure was -231.69166702 a.u., which is the same as for the gauche2 conformer correct to 6.d.p. This method, then, has proved to be quick at finding the forward reaction minimum geometry corresponding to the gauche2 conformer of 1,5-hexadiene as the kinetic product or a possible reaction intermediate after an initial 50 step IRC calculation and not the global minimum gauche3 conformer at the HF/3-21G level of theory.(Data Files)

IRC: Restart the IRC with More Steps

Inspection of the RMS gradient and .log file shows gradient convergence to zero and so the IRC with these settings will always finish at step 44 no matter how many steps the calculation is set to take. This means for this case, this method would be pointless.

IRC: Compute the Force Constant at Every n=1 Steps

Again, this method finished after 44 steps with a geometry resembling the gauche2 conformer with an energy of -231.69157820 a.u. without the need for further optimisation as for the first approach.(Data Files). So, although it has failed to find the actual minimum geometry, it shows that all three methods will output a geometry strongly resembling the gauche2 conformer with reasonably similar energies. This, then, has proven to be the best IRC method in this particular case. All of this information points in the direction of the gauche2 conformer being the adjacent minimum to this TS. The gauche2 product forms, even though it is not the global minimum, because it is the kinetic product. A kinetic product forms via a lowest activation energy transition state, which is what we have here and is shown quantitatively in the following sections, whereas a thermodynamic product typically has a higher activation energy (but in this case will be the same TS), but results in the overall global minimum product. So we can say that gauche2 is expected to be the kinetic product of the reaction that, under equilibrating conditions, should readily convert into the global minimum conformer back through the chair TS. The TS structures have been calculated at 298.15 K, recalculation at higher temperature will then show an IRC going to the lower energy conformers until finally forming the most thermodynamically stable product since there will then be sufficient energy to surmount the TS energy barrier (unlike at 298.15K)

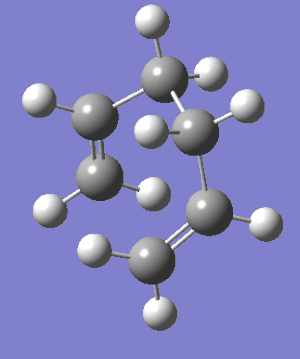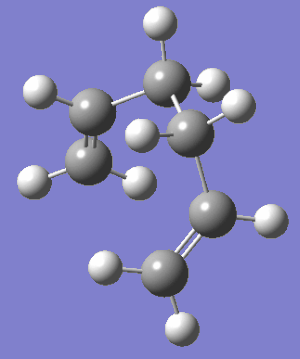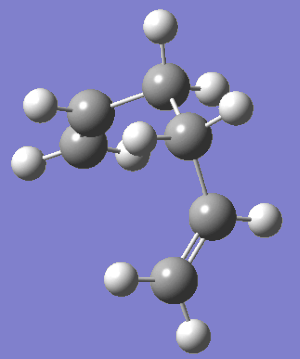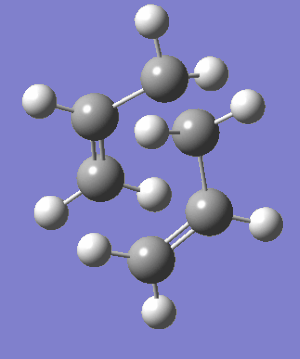
Cope Rearrangement IRC from the TS to the Gauche2 Conformer.

Reoptimisation Using DFT

The final step to take in order to quantitatively determine the reaction path from products to reactants, activation energies need to be calculated. Thus far, the chair and boat TS have been calculated at the HF/3-21H level. To find more accurate boat and char TS geometries, reoptimisation at a higher level of theory, the B3LYP/6-31G* level, must be carried out. The calculation settings used were exactly the same as for the HF\3-21G level and the input files were the chair and boat TS geometries from the HF\3-21G optimisation. As before, it is also important still to remember to inspect vibrations to ensure that the optimised geometry still has a single imaginary frequency.

The table below summarises imaginary frequencies, different energies at different temperatures for the HF\3-21G and B3LYP/6-31G* levels used in this wiki report. The Electronic energies were calculated by subtracting the zero-point energy correction from the sum of electronic and zero-point energies. Click on the structure name for data files.

	HF/3-21G Energy/ Hartrees
Structure	Electronic Energy	Sum of Electronic & Zero-Point Energy (0 K)	Sum of Electronic and Thermal Energy (298.15 K)	Imaginary Frequency/ cm-1
Chair TS	-231.619322	-231.466694	-231.461332	-817.89
Boat TS (Modified Angles QST2)	-231.602800	-231.445327	-231.444383	-838.14
Boat TS (QST3)	-231.602802	-231.450928	-231.445299	-840.01
Anti1	-231.692603	-231.539601	-231.532644	-
Anti2	-231.692535	-231.539542	-231.532570	-
Gauche2	-231.691667	-231.538704	-231.531793	-
Gacuhe3	-231.692661	-231.539486	-231.532646	-
	B3LYP/6-31G* Energy/ Hartrees
Structure	Electronic Energy	Sum of Electronic & Zero-Point Energy (0 K)	Sum of Electronic and Thermal Energy (298.15 K)	Imaginary Frequency/ cm-1
Chair TS	-234.556983	-234.414929	-234.409008	-565.65
Boat TS (Modified Angles QST2)	-234.543093	-234.402343	-234.396008	-530.26
Boat TS (QST3)	-234.543093	-234.402342	-234.396007	-530.31
Anti1	-234.611801	-234.469286	-234.461965	-
Anti2	-234.611703	-234.469211	-234.461854	-
Gauche2	-234.610708	-234.468205	-234.460939	-
Gacuhe3	-234.611329	-234.468693	-234.461464	-

Reoptimised Geometries

	Chair TS		Boat TS (QST3)
Bond	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*
C1-C1/ Å	2.02137	2.13990	1.96768	2.20685
C2-C2/ Å	2.87933	2.77952	2.90969	2.85704
C3-C3/ Å	2.02137	2.13994	1.96768	2.20669

From the data summarised in both tables above, it can be seen, as has been throughout this tutorial, that using a higher basis set and DFT does not change the geometry of the molecule significantly. However a change of method and basis set does have a dramatic effect on the calculated energies/ vibrations. B3LYP/6-31Gd, although more computationally expensive, takes into account electron correlation and so will be the more accurate method of choice for optimisations of the Cope rearrangement. For the same accuracy using the HF method, a much higher basis set would be needed, which will significantly increase the processing time needed to complete the calculations. DFT, then, allows use of higher basis sets for more accurate results as well as including electron correlation, but at a fraction of the computational expense as for other methods. It would be most efficient, then, to first optimise the geometry using the HF/3-21G method, and then reoptimising (as done here) using the B3LYP/6-31Gd method as and when needed. Also, from the geometry data, it is seen that the difference between the boat bond lengths at the two levels of theory is much greater than for the char structures. This shows that as the energy of the structures increases, the more divergent both methods are towards each other. This is logical since at higher energies, small changes/ differences have a bigger effect.

Activation Energies

At 0K there is no thermal contribution and so the sum of the electronic and zero-point energies is used for the calculation of activation energy. At 298.15K there is some thermal contribution and so the sum of the electronic and thermal energies is used for the calculation of activation energy. The activation is calculated using the difference between these energies for the reactant conformers and the chair and boat TS.

	Chair TS Activation Energy/ kcal/mol				Boat TS (QST3) Activation Energy/ kcal/mol
	HF/3-21G		B3LYP/6-31G*		HF/3-21G		B3LYP/6-31G*
	0K	298.15K	0K	298.15K	0K	298.15K	0K	298.15K
Anti1	45.749843	44.7489652	34.1095398	33.2310263	55.6431595	54.8098267	42.0080032	41.3892787
Anti2	45.7128199	44.7025295	34.0624765	33.1613727	55.6061364	54.763391	41.96094	41.3196252
Gauche2	45.186967	44.2149545	33.4312019	32.5872015	55.0802834	54.275816	41.3296653	40.7454539
Gauche3	45.6776794	44.7502202	33.7374266	32.916644	55.5709959	54.8110817	41.63589	41.0748964

From the data in the table above, it can be seen that each method correctly predicts that the chair TS activation energies are much lower than the boat TS (by about 12 kcal/mol). For all of the conditions and methods tabulated the gauche2 conformer always give the lowest activation energy, which again shows the usefulness in using the HF/3-21G method to get a general trend of properties and reaction outcomes without expensive computation. The experimental values of the activation energies at 0K are 33.5 ± 0.5 kcal/mol for the chair TS (completely consistent with DFT calculation for the gauche2 conformer) and 44.7 ± 2.0 kcal/mol for the boat TS (very close to DFT calculation for the gauche2 conformer). These are both completely consistent with the B3LYP/6-31G* level calculations, but not the HF method. This shows how accurate the DFT method is over the HF method, as discussed throughout, for larger basis sets with mild computational expense in calculating accurate energies for structures comparable to experiment. The difference between theory and experiment is that for theory, on top of approximations to make calculations possible to do, no account of other interactions such as intermolecular is taken.

Fundamentally, this tutorial has shown how far computational studies have come in predicting the reaction outcomes of highly stereo- and regio-selectiver reactions. Although the DFT method is much more accurate than the HF method, the HF method is still able to predict the overall likely reaction outcome under these conditions. But, if energies are under analysis then more time spent on higher levels of theory is necessary to get experimentally comparable results.

Diels-Alder Cycloaddition

Introduction

Otto Diels (Left) and Kurt Alder (Right): winners of the 1950 Nobel Prize for the discovery of the Diels-Alder reception.

Like the Cope rearrangement, Diels-Alder (DA) cycloaddition is a pericyclic reaction that is well studied and documented in textbooks to proceed via a [4+2] concerted mechanism via a cyclic TS forming unsaturated six-membered rings. These reactions are characterised from other pericyclic reactions by the overall breakage of two π C-C double bonds and the formation of two σ C-C bonds from diene + dienophile reactants. C-C bonds are much more stable than double bonds making this process exothermic due to such driving force.

The reaction was discovered by Otto Diels and Kurt Alder who were the recipients of the 1950 Nobel Prize for this contribution and its development in chemistry. The DA reaction has huge synthetic utility across all chemistry. Most notably the pharmaceutical and agrochemical industries where compounds typically have multiple rings. DA reaction provides mush simplification of such compounds with a very reliable and predictable reaction.

The simplest Diels-Alder Reaction is the reaction between 1,3-butadiene (diene) and ethylene (dienophile) to yield cyclohexane as shown in the scheme below.

The reaction can occur with two different types of electron demand: normal or inverse. The energies of the HOMO and LUMO of both reactants will determine if the reaction is allowed or forbidden and the type of electron demand. Normal electron demand occurs when the electron rich diene (EDG substituents) donates its HOMO electrons to the LUMO of the electron deficient dieneophile (EWG substituents) where the choice of substituents maximises the interaction between the HOMO and LUMO (brings them close in energy). Using the simplified Klopman-Salem expression below (derived from perturbation theory), it can be seen that the closer orbitals are in energy, the better they interact and the greater the stabilisation energy due to the interaction, where S is the overlap integral and ΔE is the difference in energy between interacting orbitals:

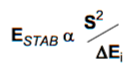
Inverse electron demand is the opposite, where the EWG is on the diene and EDG on the diene to bring the HOMO and LUMO orbitals closer together. If the HOMO and LUMOs are sufficiently close in energy; have the same symmetry for effective orbital overlap and the overall reaction will lead to stabilisation then the reaction is allowed. Substituents that modify the energy levels of the reactants also play a role in the region-selectivity of the reaction of which will be studies using computational methods in the proceeding discussion.

Although the reaction between 1,3-butadiene and ethylene is known to be concerted ^{Citation Needed}, theoretical studies of the alternative stepwise pathway shows that the TS of the stepwise process is not a lot higher in energy than the concerted pathway, 2.3 to 7.7 kcal/mol ^{Citation Needed}. This means it is important to study substituted versions on a case by case basis since they may proceed via a stepwise process depending on the interactions as a result of the substituents and possible secondary orbital interactions between them. The nature of the TS will elucidate the reaction mechanism and the prediction of endo- or exo- products.

(Very good introduction. Perhaps make a stronger point about the symmetry - the reaction is forbidden unless the interacting orbitals share the same symmetry ^{Citation Needed}. At the moment you've only put this in the inverse DA paragraph. As you've spoken about stepwise reactions of dienes and dienophiles, have you tried finding the TS's? Tam10 (talk) 12:33, 11 December 2015 (UTC))

Aims

• Optimise the cis-butadiene geometry
• Plot the HOMO-LUMO of cis-butadiene and deduce its symmetry
• Computation of the TS geometry for the prototype reaction and examine the nature of the reaction path
• Study the nature of the transition structure for the substituted Diels-Alder reactions
• Study the regio-selectivity of the Diels Alder reaction using secondary orbital interactions

Computational Methods

Semi-Empirical Methods

The methods used in this study are based on improving the limitations of the HF method. Namely, the speed and accuracy. This is done by implementing know experimental data so as to omit interactions that aren't necessarily important to calculate/ don't hugely contribute to the overall energy and geometry (eg. dipole moments and ionisation energies). The two-electron multi-centre integrals are negated to simplify the Hamiltonian to the consideration of only the valence shell electronsThis negates large parts of the quantum mechanical ab initio HF method, which makes it significantly quicker and can therefore be applied to large molecules. The semi-empirical methods used in this study use zero-differential orbital (ZDO) basis sets. A drawback of these methods is that, since experimental data is being used to simplify the calculations, if the data for the reaction under analysis is unique and not on the database, then geometries won't be an accurate depiction of reality.

Austin Model 1 (AM1)

This method simplifies the HF calculations by approximating two-electron integrals and adapting the calculation of core repulsion, which results in an expression for non-physical favourable interactions similar to van der Waals. AM1 has been shown to improve on HF for the calculation of heats of formation. However, systematic over-estimates of basicities means AM1 still has its limitations.

(Could you expand that last sentence? Tam10 (talk) 12:33, 11 December 2015 (UTC))

Diels-Alder Reaction Between cis-Butadiene and Ethene

Optimisation of cis-Butadiene

cis-Butadiene structure built in Gaussview with C_2v symmetry

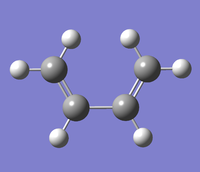
The first step in the theoretical analysis of this DA reaction was to optimise cis-butadiene. This was done using the AM1 semi-empirical method.

First, cis-butadiene was built by putting four carbon atoms in a cis- formation with the appropriate H atoms around them and then using the Modify Bond tool to implement the appropriate bonding between the atoms. The structure was then cleaned up using the Clean function too arrive at the cis-butadiene structure shown to the right with C_2v symmetry. This structure was then optimised using the AM1 method with the opt+freq job type. The Data files can be found here. Vibrational analysis shows an imaginary frequency at -39.43 cm-1, so already the limitations of AM1 are visible. Such vibrational frequency can be viewed here. A plot of the optimised cis-butadiene HOMO and LUMO is shown below. Symmetry is relative to the axis of highest symmetry (principal axis): the z axis.

cis-Butadiene antisymmetric (a) HOMO

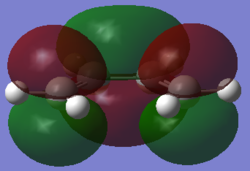
cis-Butadiene symmetric (s) LUMO

Optimisation and Analysis of cis-Butadiene + Ethylene TS

Ethylene was built in Gaussview with two sp² carbon fragments and then optimised using the AM1 method with the opt+freq job type again. Data files can be found here. There were no imaginary frequencies (as expected) and the HOMO and LUMO of ethylene are shown below with the associated symmetry.

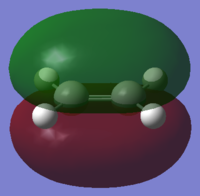
ethylene symmetric (s) HOMO

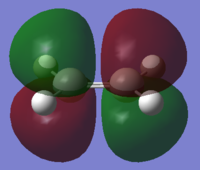
ethylene antisymmetric (a) LUMO

	cis-Butadiene	Ethylene
HOMO Energy/ kcal/mol	-215.74181	-243.31429
LUMO Energy/ kcal/mol	10.71148	33.15729

(Be careful here - the orbital energies are in eV not Hartrees. You're showing band gaps of 200-300 kcal/mol. Tam10 (talk) 12:33, 11 December 2015 (UTC))

From MO theory and as was discussed in the introduction, orbitals must have the same symmetry for there to be sufficient orbital overlap and stabilisation energy (ie. so the overlap integral, S, is not zero). This means that for the reaction between cis-butadiene and ethylene, the possible frontier orbital interactions leading to the reaction TS are butadiene HOMO+ethylene LUMO or butadiene LUMO+ethylene HOMO. From the energy data in the tables above, the smallest energy gap out of these two is between the HOMO of butadiene and the LUMO of ethylene (248.89910 kcal/mol cf. 254.02577). This is normal electron demand. From FMO theory, the best overlap of these approaching orbitals is from above each other so as to maximise the orbital overlap between the ethylene π* and cis-butadiene π orbitals. From this knowledge, a guess TS was drawn. This structure was first optimised using HF to 'clean up the orientations' and then optimised to a TS (Benry) with the AM1 method and calculating force constants once with the additional key words opt=noeigen as shown below. Data files for AM1 optimisation here. The single imaginary frequency at -955.98 cm-1 confirms that this structure is a transition structure with an energy of 70.06363411 kcal/mol.

Guess TS	Imaginary Frequency Vibration at -955.98 cm-1 leading to the Diels-Alder reaction after AM1 optimisation	Lowest Real Imaginary Frequency at 147.32 cm-1

TS antisymmetric (a) HOMO

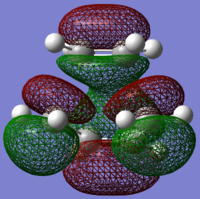
TS symmetric (s) LUMO

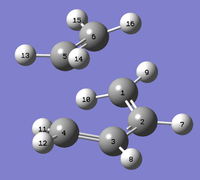
Labelled TS

Analysis of TS Geometry

To investigate whether the formation of the TS is synchronous or not, quantitatively, other than just by looking at the imaginary frequency the bond lengths of the forming/ breaking bonds were measured. If they are both the same length then this gives a good indication that the process is synchronous. Also from the bond lengths we can deduce whether the formation of the TS is concerted. For this to be so, the bonds all around the ring will all be very similar lengths (intermediate of C-C and C=C bonds) to show some delocalisation, but not aromaticity.

	Bonds Breaking/ Å	Intermediate Bonds/ Å	Bonds Forming/ Å
C1-C2	1.22394	1.38185	1.59856
C2-C3	1.57749	1.39749	1.21749
C3-C4	1.22395	1.38185	1.59856
C4-C5	2.78778	2.11937	1.45208
C5-C6	1.12290	1.38290	1.64290
C6-C1	2.78777	2.11936	1.45207

As has been found in other experiments, the C1-C2 (and C3-C4) intermediate bonds are almost exactly equal to the C2-C3 bond length (only 0.01564 Å difference), which is in line with a delocalised TS characteristic of concerted mechanisms. The intermediate bond length in the ethylene component, C5-C6, is also very similar to the butadiene component with a difference of just 0.00105 Å. This means that each bond of both components has approximately the same bond length. Although this is not confirmation for a concerted TS since the C4-C5 and C6-C1 bonding interactions are much larger (non-aromatic nature). Also it can be seen that the C1-C2 and C3-C4 bond lengths are always exactly the same throughout the formation of the TS. This indicates the synchronous nature of the reaction previously discussed.

Typical C-C bond lengths are summarised below:

Summary of different C-C bond lengths.

Using this data, it can be seen that the the C2-C3 bond forming corresponds to the formation of an sp²-sp² C=C bond. The others all show character of forming sp³-sp₃ C-C bonds. This is consistent with the know reaction outcome, where the formed cyclohexene consists of just a single double bond. For the intermediate bonds, the C4-C5 and C6-C1 aren't actually formal bonds yet. The van der Waals radii of carbon atoms is 1.7 Â. When considering bonding interactions, twice the radii van der Waals radii needs to be considered (one contribution from each atom involved in the interaction). This means that carbon atoms will start to interact at a distance of 3.4 Å apart. The tabulated bond lengths found for this reaction at the AM1 level are all much lower than this value, which means there is considerable interaction throughout the formation of the TS between the C4-C5 and C6-C1 carbons (moving towards a formal bond).

The IRC for the both reaction directions from the TS was calculated at the AM1 level using 100 steps and calculating the force constant always. The output from this calculation gave an IRC path that was opposite to the real reaction direction (products-TS-reactants). To overcome this, the data from the .log file was imported into excel, data inverted by taking the negative of the reaction coordinates and then replotted. The corrected IRC is shown below with the reaction animation, which shows the concerted synchronous TS formation. Data files for the IRC can be found here.

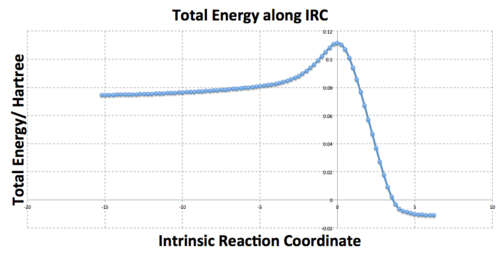
IRC for the reaction between cis-butadiene and ethylene at the AM1 level.

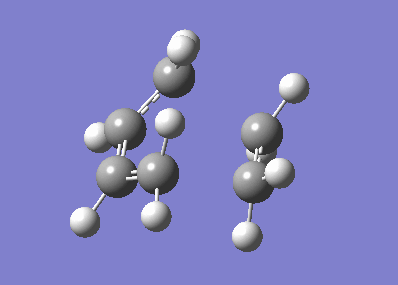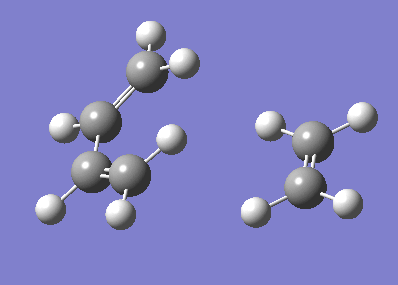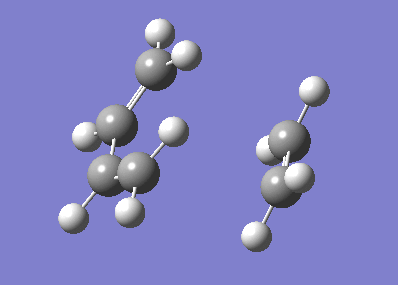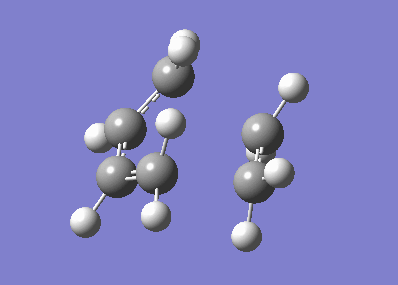
Forward reaction animation.

s-trans and s-cis Butadiene

From the IRC, the reaction seems to be highly exothermic, so why is the reaction generally carried out at elevated temperatures? The answer is because of the very specific geometry in which the reactants must be oriented on approach to each other. Also butadiene must be in the cis- conformation, but this is much higher in energy than the trans- form and so pretty much all of butadiene exists as the trans- form. The trans form does not have the appropriate orbital symmetry for DA reaction with ethylene. Trans-butadiene was optimised at the AM1 level. The MOs of trans-butadiene are shown below. No imaginary frequencies were found. Data files for this optimisation can be found here.

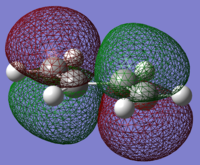
trans-butadiene HOMO

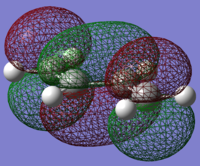
trans-butadiene LUMO

Using the AM1 method, the energy of trans-butadiene was found to be 29.84585 kcal/mol cf. 30.62038 kcal/mol. This means the s-trans- form is not that much more stable than the s-cis form. Further investigation was carried out by performing a QST2 for the interpolation of the interconversion of s-trans and s-cis conformers (using appropriate atom labelling) to find the TS for the conversion. This structure was then optimised to a TS (Berny) and a single imaginary frequency was found at -85.27 cm^-1 confirming it as a TS. Data file here. A basic reaction profile was plotted using the sum of the electronic and thermal energies thermochemistry data of each structure using excel. The energies were converted into kJ/mol and the plot is shown below.

(The difference in energy that you've calculated is less than 1 kcal/mol which isn't too much. In reality it should be higher, but AM1 is underestimating it. Tam10 (talk) 12:33, 11 December 2015 (UTC))

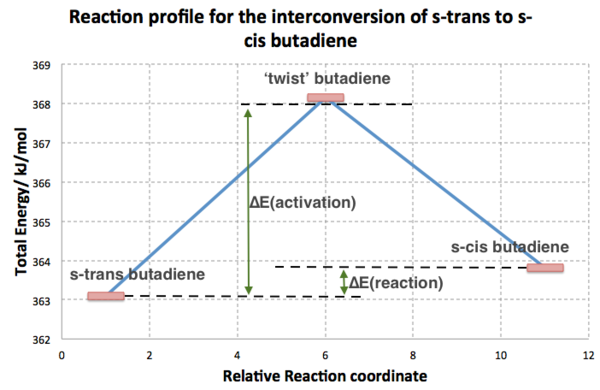
s-trans butadiene	'twist' butadiene	s-cis butadiene

(You should normalise these energies - the absolute value has no real meaning. Tam10 (talk) 12:33, 11 December 2015 (UTC))

From the profile, the activation energy is approximately 5 kJ/mol, but experimentally it is actually higher than this, but nevertheless shows the same idea. This energy barrier means that about 96% of butadiene exists as the s-trans conformer and so to get any appreciable reaction rate for the DA reaction, high temperatures are needed so that the barrier can be readily surmounted.

Diels-Alder Reaction Between Cyclohexadiene and Maleic Anhydride

The Diels-Alder reaction is stereospecific. This means that the stereochemistry is conserved in the products (i.e. trans to trans and cis to cis etc.). In more complex DA reactions where there are substituents attached to a diene and dieneophile this stereospecificity becomes important; this is because in these cases, there will be the possibility of forming two different products (exo or endo). Of these there can be enantiomeric forms too since approach of the dienophile to the diene orbitals can be from above or below the plane of the diene.

Reaction scheme for the DA reaction of 1,3-cyclohexadiene with maleic anhydride

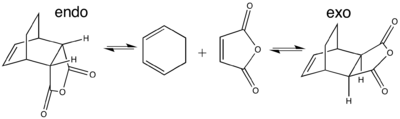
The initially proposed rules for predicting the outcomes of these more complex reactions was presented by Alder and Stein, which states that the endo product should be the only formed product. The currently accepted theory was proposed by Woodward and Hoffmann, which is based on secondary orbital interactions and the conservation of orbital symmetry:

'In allowed thermal pericyclic reactions the number of (4q+2)s and (4r)a components must be odd.'

These rules, however, have been called into question due to possible dispersion and steric interactions that may also be involved in the selectivity, but are not accounted for by the Woodward-Hoffman rules. This means that computational studies on the DA reaction, although well studied experimentally, are still important to help understand reaction selectivity. This is important in synthetic chemistry since you can predict the outcome of a reaction before it is performed.

The reaction between cyclic dienes (such as 1,3-cyclohexadiene) and maleic anhydride is extremely facile and results in an kinetic endo adduct major product where the TS for the thermodynamic exo product is expected to be higher in energy.

Optimisation of 1,3-Cyclohexadiene and Maleic Anhydride

Optimisations were, again, carried out using the AM1 method and their HOMO-LUMO calculated orbitals are shown below.

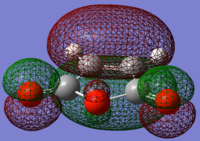
	Maleic anhydride symmetric HOMO	Maleic anhydride antisymmetric LUMO	Data Files.
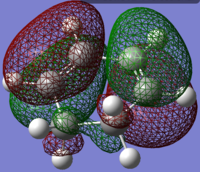
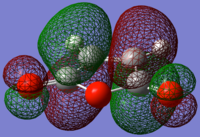
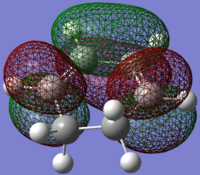
	1,3-Cyclohexadiene antisymmetric HOMO	1,3-Cyclohexadiene symmetric LUMO	Data Files.

From the symmetry of the above orbitals for the optimised reactants, the two possible interactions that will lead to a DA reaction are between the symmetric HOMO of maleic anhydride and the symmetric LUMO of 1,3-cyclopentadiene (287.81 kcal/mol energy difference) or the antisymmetric LUMO of maleic anhydride and the antisymmetric HOMO of 1,3-cyclohexadiene (164.69 kcal/mol energy difference). As was done for the prototypical DA reaction, the interaction that will occur will be the one in which the orbitals are closest in energy (using the Klopman-Salem simplified equation) so that the stabilisation energy is maximised. Comparing the energy differences of the HOMOs and LUMOs in this case, the reaction is expected to proceed via the interaction of the interaction of the antisymmetric LUMO of maleic anhydride and the antisymmetric HOMO of 1,3-cyclohexadiene. This interaction is normal electron demand, but is more facile than previously seen due to the substituents. The carbonyl substituents on maleic anhydride are EWG which lowers the energy levels (LUMO moves lower=closer in energy to the cyclohexadiene HOMO).

Exo Transition Structure

The exo transition structure was built using a guess from the combination of the optimised 1,3-cyclohadiexene and maleic anhydride reactants from above. This initial guess structure was then optimised to a TS (Berny) with the AM1 method. Vibrational analysis showed a single imaginary frequency at -812.27 cm-1, which confirms that this is a transition structure. This vibration is shown below. Data Files.

The geometry of this TS was then analysed using bond lengths as for the previous DA reaction studied. This data is tabulated below.

	Bonds Breaking/ Å	Intermediate Bonds/ Å	Bonds Forming/ Å
C1-C2	1.24519	1.39441	1.62391
C2-C3	1.57674	1.39674	1.21674
C3-C4	1.24513	1.39438	1.62390
C4-C5	2.88894	2.17043	1.45243
C5-C6	1.15013	1.41013	1.67013
C6-C1	2.88854	2.17001	1.45199

From the intermediate bond lengths it can be seen that C1-C2-C3-C4 bond lengths are all approximately the same at around 1.4 Å. This means that there is delocalisation across these bonds, which indicates a concerted nature of this mechanism. 1.4 Å is only slightly larger than that known for the average sp²-sp² C=C bond. All of the bond lengths tabulated are less than twice the vdw radii of a C atom, so even if there are no formal bonds between C4-C5 and C6-C1, there is still strong electronic interaction. The TS formation may be synchronous too since the C4-C5 and C6-C1 bonds being formed consistently have a difference of approximately 0.0004 Å thought the bond forming process.

The TS HOMO and LUMO are shown below. As can be seen, the symmetry of the interaction of the diene and dieneophile has conserved orbital symmetry.

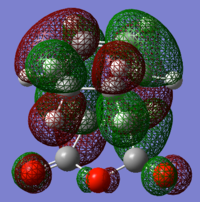
exo TS antisymmetric HOMO

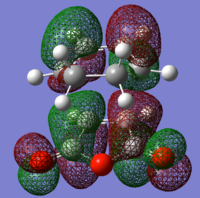
exo TS antisymmetric LUMO

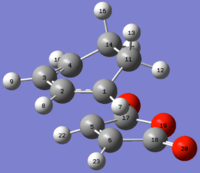
Labelled exo TS

Endo Transition State

The optimised endo transition state was found to have a single imaginary vibrational frequency at -806.38 cm-1 shown below. Data Files.

The bond lengths, as before, are as follows.

	Bonds Breaking/ Å	Intermediate Bonds/ Å	Bonds Forming/ Å
C1-C2	1.24665	1.39306	1.61767
C2-C3	1.57724	1.39724	1.21724
C3-C4	1.24665	1.39305	1.61767
C4-C5	2.85790	2.16239	1.46937
C5-C6	1.16849	1.40849	1.64849
C6-C1	2.85790	2.16239	1.46937

Bond distances are similar to the exo transition structure and the same conclusions can be drawn from their analysis. The TS HOMO and LUMO are shown below. As can be seen, the symmetry of the interaction of the diene and dieneophile has conserved orbital symmetry.

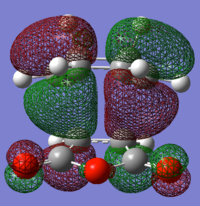
endo TS antisymmetric HOMO

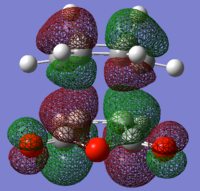
endo TS antisymmetric LUMO

Comparing Exo and Endo: The Orbital Picture

Instinctively on first glance at the two TS it would be expected that the endo TS would be higher in energy due to the higher steric gauche interactions in the geometry as compared to the exo. However, comparing the energy of each TS (endo=-31.639 kcal/mol cf. exo=-32.319 kcal/mol) the endo TS is actually lower in energy. There must be large favourable interactions that are possible in the endo TS and not in the exo TS that can overcome the steric interactions and more! To investigate this, MOs must be visualised.

From orbital analysis there seems to always be many nodal planes in the HOMO. However nodes at atoms are less energetically contributing than between atoms (and most of them in the HOMO are on the atoms) so many of these nodes don't contribute significantly to the overall energies. It can also be seen that only the endo transition structure has stabilising secondary orbital interactions (SOI). These orbital interactions, though, are not typical since they appear not to be involved in the formation of bonds between the two reactants, but rather a redistribution of π electrons in the π system. These interactions are, however are close to the limit of twice the vdw radii and so are not as strong as first might be expected and in other systems, other interactions may perturb this interaction and is not sufficient in this system to explain the great preference for endo over exo. To explain this, further data must be considered such as product distribution, free energy and solvent models, activation energy, rate constants, activation energy and temperature. An understanding of the combination of all of these effects is needed to fully explain the results of a DA reaction. This shows how this simple reaction has some very complex underlying driving forces for the formation of one product over another.

(Perhaps reorientate the MOs to demonstrate this paragraph. Or use jmols to show the orbitals. Tam10 (talk) 12:33, 11 December 2015 (UTC))

Activation Energy

The energy of the reactants is given as there sum of the data for the individual optimised structures. The data used is the sum of the electronic and thermal energies.

	Reactants/ kcal/mol	TS/ kcal/mol	Products/ kcal/mol	Activation Energy/ kcal/mol
Exo	62.457	90.915	25.395	28.458
Endo	62.457	90.162	25.395	27.705

The first point to notice is that the AM1 method has correctly predicted that the exo product is lower in energy and so will be expected to find accumulation of this product over a long period of time and at elevated temperatures. The second inference is that the energy of the Endo TS is only 0.753 kcal/mol more stable than the exo TS, which means that the previous discussion on the SOI's not being the determining factor in this reaction, possibly from being too far apart, is consistent with this data. The reaction profiles shown below are virtually completely superimposed on each other with just the difference of a different TS energy (and hence Eact). Product geometries were found by performing and IRC and then optimising the final structures using AM1. Exo product Data Files. Endo product Data Files.

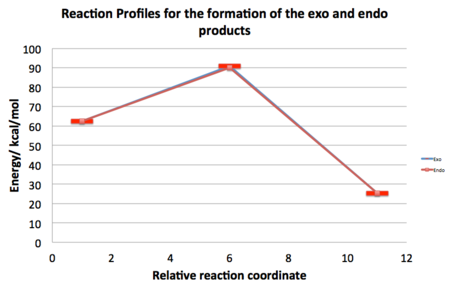
It is interesting to note that for a similar reaction between cyclopentadiene and maleic anhydride, the exothermicity is much less. This is attributed to the aromaticity of the cyclopentadiene (furan). So although we have seen that there are some SOI that should be considered, there are also many other factors that will need to be considered to get a full picture of what is happening during these elegant reaction types.

For a deeper insight with less time constraints, the following properties should be investigated (neglected in this study):

Property	Discussion
Entropy	Although for this reaction is is expected that the entropy of both will be approximately the same, for more complex unknown reactions, an entropic driving force is possible and so should be considered.
Enthalpy & Gibbs Free energy	Differences may arise from plotting these reaction profiles rather than using the total energy of the substances. It is expected that the exo TS free energy will be higher in energy again.
Product distribution	Using a Boltzmann distribution
Activation Energy
Rate Constants
Equilibrium constants
Temperatrue Effects	It is expected that as the temperature of the calculation is increased, the yield of the reaction decreases. This is because the entropic contribution to the free energy will no longer be negligible. In fact the entropy will be negative (retro-DA becomes more favourable).Citation Needed
Investigate a wider variety of substituents and reactants in general
Repeat calculations using a more accurate method or another semi-empirical method such as PM3 (Parameterised Model number 3)

Conclusion

This whole study has shown the power of using computational programs such as Gaussian to implement numerical quantum calculations in predicting and explaining the underlying nature of reaction mechanisms. Such studies are every increasing to be paramount in both industrial and research applications. It has also been shown that there is not one method that is best in all situations and a good knowledge of what the methods actually do is needed for choosing which method is best implemented to probe reaction details. In the tutorial for the Cope rearrangement is was found that the Chair TS is lower in energy than the Boat TS. The energies of different conformations of starting material were also analysed. This was done using two different computational methods. The end result was that DFT is quicker than HF using larger basis sets and more accurate because it accounts for electron correlation. However using larger basis sets (which is common) for DFT means that they are more computationally expensive. This means that optimisations should be carried out using HF/3-21G first and then using the higher levels of theory when it is necessary. The semi empirical is less accurate than both HF and DFT methods (although it does consider electron interactions). It was used in the second half of the study in place of the other methods since more complex reactions will make DFT and HF calculations very slow. Again, for more accurate energies that are comparable to experiment, allowing for more computational processing time will be necessary.

The study of the DA reaction stereoselectivity showed that although SOI do have some influence on the exo or endo outcome, it may not be the only factor and in more complex reactions, the SOI may be negligible or easily countered by other effects.In this study, however, it was correctly found that the exo TS lies slightly above the endo TS in energy and so the prevailing kinetic product will be the endo product (lowest activation energy).

Further analysis of this reaction using these properties may elucidate new tools to describe these reactions, which may reveal other novel ways of using the high degree of stereoselectivity that is currently not explained convincingly.