Rep:Mod:135197471
NH3
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -56.5575579 a.u.
Point groups: C3V
N-H bond length: 1.101798 Å
H-N-H bond angle: 105.745 degrees
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000009 0.001200 YES
NH3 |
The optimisation file is linked to here
Questions
1)how many modes do you expect from the 3N-6 rule?
6 modes of vibration as there are 4 atoms in the molecule as it is non-linear: (3*4)-6 = 6.
2) Which modes are degenerate (ie have the same energy)?
2 and 3 are degenerate with respect to each other, as are 5 and 6.
3) Which modes are "bending" vibrations and which are "bond stretch" vibrations?
1, 2 and 3 are bending vibrations while 4, 5 and 6 are stretching.
4) Which mode is highly symmetric?
Mode 4 involves each bond stretching in the same direction by the same amplitude simultaneously.
5) One mode is known as the "umbrella" mode, which one is this?
Mode 1.
6) How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
3 bands, as there are 4 distinct frequencies at which the molecule vibrates but modes 5 and 6 have very small intensities and would not be easily visible in the spectrum.
The charge on nitrogen is -1.125 and 0.375 for hydrogen. This aligns with what is expected as nitrogen is more electronegative than hydrogen so will withdraw electron density giving it a negative charge whilst hydrogen has a positive one.
H2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -1.1785394 a.u.
Point groups: D*H
H-H bond length: 0.74279 Å
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
All values have converged as they are below the threshold.
H2 |
The optimisation file is linked to here
There are no negative frequencies therefore the energy is at a minimum.
N2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -109.5235911 a.u.
Point groups: D*H
N-N bond length: 1.10550 Å
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
All values have converged as they are below the threshold.
N2 |
The optimisation file is linked to here
There are no negative frequencies therefore the energy is at a minimum.
Haber Process Enthalpy Change
E(NH3)=-56.55755789
2*E(NH3)=-113.1151158
E(N2)=-109.52359111
E(H2)=-1.17853936
3*E(H2)=-2.35707872
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.05590659
-0.0559066 Hartrees = -146.78 kJ/mol
Since the reaction has a negative enthalpy change, energy is released in the reaction. As a result, the product is more stable than the reactants.
The literature value for NH3 enthalpy of formation is -92.44 kJ/mol [1]
F2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -199.49825218 a.u.
Point groups: D*H
F-F bond length: 1.40281 Å
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES
All values have converged as they are below the threshold.
F2 |
The optimisation file is linked to here
There are no negative frequencies therefore the energy is at a minimum.
There is no charge on either atom as they are identical so electron density is shared equally between them
Orbitals
Orbitals and Energies
2s
This is the 2s bonding orbital. It is quite deep in energy at -1.33659, but still much higher in energy than 1s. It is occupied by 2 electrons and there is good overlap between the atomic orbitals.
2s*
This is the 2s* anti-bonding orbital. It is quite deep in energy at -1.09047, but less stable than the corresponding bonding orbital due to the lack of overlap between each atomic orbital. The lack of overlap is caused by the phases of each atomic orbital being opposed. It is occupied by 2 electrons.
2pz
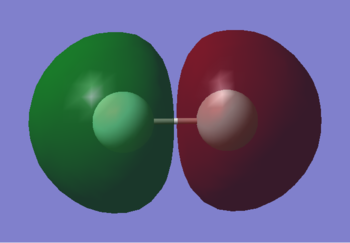
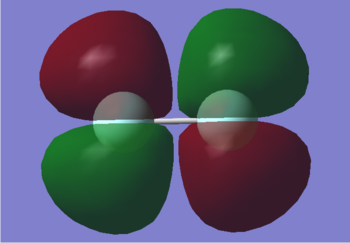
This is the 2pz bonding orbital (z is the axis in the plane of the bond). It is higher in energy than the 2s at -0.58753. Even though both orbitals have the same principal quantum number, they have different orbital angular momentum quantum numbers and the different shape causes it to be higher in energy. It is occupied by 2 electrons. It is lower in energy than 2py as the atomic orbitals that form it point along the same axis so lobes of the same phase have very good overlap between the nuclei, decreasing the orbital energy.
2py
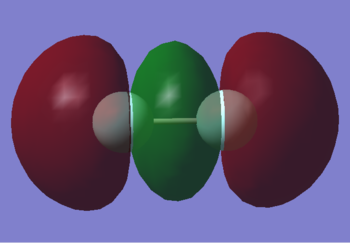
This is the 2py (y is an axis perpendicular to the plane of the bond) bonding orbital. It has an energy of -0.52332, which is higher than 2pz as the atomic orbitals do not have as much overlap. It is occupied by 2 electrons. It has the same energy as 2px and so is degenerate. Both orbitals have the same shape and overlap, they are just in perpendicular planes.
2py*
This is the 2py* anti-bonding orbital. It is higher in energy than the corresponding bonding orbital at -0.39190 due to poor overlap of atomic orbitals. It is the HOMO along with the 2px* anti-bonding orbital with which it is degenerate. The phase of the atomic orbitals that are adjacent are opposite, preventing overlap. It is occupied by 2 electrons.