Rep:Mod:130290nayr
The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations
Aim
The aim of this experiment is to use molecular mechanics to predict the geometry and regioselectivity of small molecules using ChemBio3D (MM2). This will produce an energy (in kcal mol-1) together with optimised values for bond lengths, angles etc. Hence, rationale of predominate for the reactions will be deduced. In addition, semi-empirical and DFT molecular orbital theory will be used to investigate the regioselectivity of an electrophonic chloro-substituted bicyclic diene reaction, in conjunction with another known reaction reported in literature.
The Hydrogenation of Cyclopentadiene Dimer
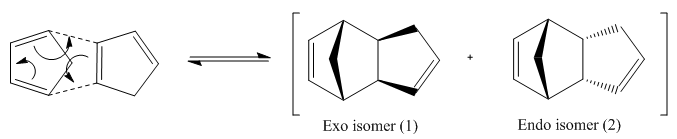
The dimerisation of cyclopentadiene proceeds under thermal conditions via a suprafacial [π4s + π2s] Diels-Alder cycloaddition with a Huckel Transition state and produces 2 isomers - the exo and endo isomer:
| Isomer | Exo (1) | Endo (2) |
|---|---|---|
| Stretch | 1.28 | 1.25 |
| Bend | 20.37 | 20.66 |
| Stretch-Bend | -0.83 | -0.83 |
| Torsion | 7.69 | 9.51 |
| Non-1,4 VDW | -1.42 | -1.51 |
| 1,4 VDW | 4.25 | 4.30 |
| Dipole/Dipole | 0.38 | 0.44 |
| Total Energy/ kcal/mol | 31.70 | 33.83 |
The table shows the energies of both isomers which were deduced using the MM2 force field on ChemBio3D. It can be seen that the exo isomer (1) corresponds to a lower energy, by approximately 2kcal/mol overall, in comparison to the endo isomer (2). Thus, from a thermodynamic aspect, the exo isomer is the most favourable. This is because it is less torsionally strained since it is in the anti-periplanar configuration whilst the endo isomer exists in a gauche configuration.
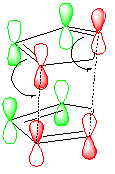
However, the higher energy endo-isomer predominates [1]which is the kinetic product and therefore the reaction must proceed under kinetic control. Under kinetic control the reaction is irreversible and depends on the transition state energy. It will have a lower energy TS but higher energy product. In this case, kinetic control predominates due to the stabilisation of the TS due to second orbital overalap interactions which will lead to an increase in constructive interference of the two orbital wavefunctions. This does not occur for isomer (1) and is shown diagrammatically below. The red orbitals overlap to form new sigma bonds and the green orbitals are the secondary interactions.
Hydrogenation of Cyclopentadiene Dimer
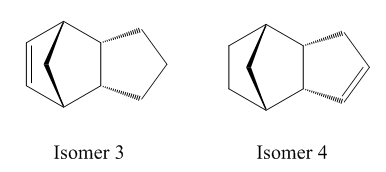
The hydrogenation of the predominate isomer (2) can form two separate products. These differ by account of which double bond is hydrogenated. The two isomers formed can be seen below, along with their corresponding energies (table 2). It is only after a long time when the tetrahydro derivative is formed.
| Relative Contributions | Isomer 3 Energies (kcal/mol) | Isomer 4 Energies (kcal/mol) |
|---|---|---|
| Stretch | 1.27 | 1.35 |
| Bend | 18.89 | 12.83 |
| Stretch-Bend | -0.84 | -0.56 |
| Torsion | 11.14 | 12.43 |
| Non-1,4 VDW | -1.65 | -1.34 |
| 1,4 VDW | 5.79 | 4.43 |
| Dipole/Dipole | 0.16 | 0.14 |
| Total Energy/ kcal/mol | 34.76 | 29.04 |
The difference in overall energy of the two molecules is approximately 4.5 kcal/mol, with isomer (4) being the lowest of the two. Hence, this isomer will be the thermodynamically favourable product. This conclusion is also supported by considereing the energy of the initial endo product in the previous section discussion. The energy of isomer (3) is higher than the endo product energy, but is lower than this for isomer (4) indicating that isomer (4) predominates.
The reason that isomer (4) is lower in energy can be understood when considering the independent energy terms which are very similar for both isomers but is considerably different for the bending term. The energy associated with the bending is smaller for product (4) which indicates that these bends are closer to the ‘natural’ bending modes due to the geometrical features of the molecule. This can be understood by analysing the bond angles around the double bond for each sp2 carbon. For isomer (4), the C=C-C bond angles are 113.0/112.40 whilst for isomer (3) the angles are both 107.6o. As a result, for isomer (3) the angle deviates furthest away from the most stable angle of 120o and consequently increases the overall energy of the molecule. Consequently, with larger bond angles formed in isomer (4), the strain released on the bridging methyl group will be greater then isomer (3). The larger angles will ensure that the the angle between the C-CH2-C bridging group is closer to 1090 for which the geometry is most favourable.
Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)
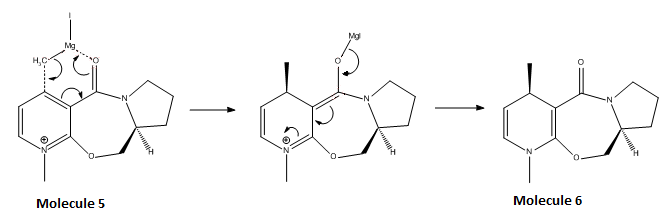
In the following reaction, the optically active derivative of prolinol (5) reacts with MeMgI to alkylate the pyridine ring in the 4-position, with the absolute stereochemistry shown in molecule 6:
| Molecule 5 | Molecule 6 | ||||||
|
|
The chelation of the Grignard reagent to the oxygen atom makes this particular reaction highly regio- and stereoselective with the driving force primarily due to the removal of the positive charge on nitrogen.
For this reaction the MM2, MMFF94, and MOPAC molecular orbital method was used to calculate which geometry is the most stable. The use of MM2 and MMFF94 methods are not capable of successfully calculating energy minima because by default the programmes give the most stable structures based on symmetry and it is this default behaviour that corrupts the minima from being calculated. This primarily arises from the N+ atom. However, MM2 and MMFF94 was still used initially to configure the general structure of the molecule so that later calculations were made easier.
The MeMgI was not included in the calculations because the programme does not have specific parameters defined for heavy metal atoms (e.g. bond lengths, force constants etc.) but does only for carbon, hydrogen, nitrogen, oxygen, sulphur, and halogens. If included, an error message (‘No atom type was assigned’) is observed. More powerful programmes need to be used if the Grignard reagent is to be incorporated. Once successfully included, the total energy of the molecule would be increased.
The energy of molecule 5 was minimised and the geometries within the molecule were varied by moving multiple atoms around (changing angles) and calculating the energy minima again. The results are shown in Table 3 below. This was done by changing the conformation from a chair to twist-boat to boat isomer. The reported dihedral angle is the one between the carbonyl group and the carbon atom in which the methyl group is attached.
| Energy kcal/mol | Dihedral Angle/ o |
|---|---|
| 93.72 | 28.87 |
| 93.61 | 25.78 |
| 101.85 | 17.89 |
| 101.02 | 16.96 |
| 102.71 | 14.02 |
The table clearly shows that as the angle becomes smaller, the overall energy increases. But, the dihedral angles are always positive indicting that the carbonyl oxygen always lies above the benzyl ring. This explains the stereocontrol of the reaction and the stereochemistry of the final product 6. Since the carbonyl oxygen always lies above the plane, the electrophilic Mg will always attack above the plane also. Consequently, the methyl group will always be attached to the ring above the plane (to give a wedged bond). The methyl group on the Grignard is a relatively small group so steric hindrance between the methyl group and the carbonyl group will be small when they are attacking on the same side of each other.
In the second reaction, the pyridinium ring of molecule 7 is reacted with aniline to form molecule 8. The mechanism is shown below:
| Molecule 7 | Molecule 8 | ||||||
|
|
Like before, the energy of molecule 7 was minimised and the geometries within the molecule were varied by moving multiple atoms around (changing angles) and calculating the energy minima again. The results are shown in Table 4 below. The reported dihedral angle is the one between the carbonyl group and the carbon atom in which the analine group is attached.
| Energy kcal/mol | Dihedral Angle/ o |
|---|---|
| 155.51 | 41.07 |
| 155.49 | 41.59 |
| 156.54 | 43.65 |
| 151.03 | -37.43 |
| 150.84 | -39.02 |
The table above shows that for the lowest energy configurations, the dihedral angle has to be negative. This means that the carbonyl oxygen has to lie behind the benzyl ring.
This reaction undergoes stereospecific control. The reason for this is because of steric hindrance. The incoming analine molecule is electron rich (lone pair on nitrogen) and bulky and the oxygen from the carbonyl group is also electron rich (lone pair on oxygen). These two electron clouds will repel each other and thus influence the direction of reactivity. In this case, to minimise the repulsion the analine will attack on the opposite side of the ring of where the carbonyl oxygen exists. Consequently, since the carbonyl group is approximately 37o below the ring, the analine will always attack from above the ring (and give a wedged bond) to form the stereospecific molecule 8.
To improve the calculations, the magnesium atom needs to be incorporated. These 'new' bonds will have an effect on the energy minima by increasing them slightly. In some cases, the ordering of the energies for each conformation may change slightly and hence the understanding of the most stable isomer may change. Programmes that allow heavy metal atoms in the calculation include Gaussview which works from the Density Function Theory Method.
Furthermore, an improvement was already made initially by using MOPAC rather than simple molecular mechanics which ignores stereoelectronic factors particularly in transition states. MOPAC uses data derived from molecular orbitals rather than simply using force constants etc...
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
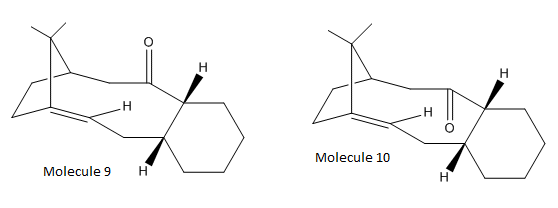
The synthesis of taxol has become increasingly important for medical uses. The intermediates of the reaction can be seen as molecule 9 and 10 below:
| Molecule 9 | Molecule 10 | ||||||
|
|
Molecules 9 and 10 are isomers of each other (known as atropisomers) and isomerise to the alternative carbonyl molecule upon standing[2]. Atropisomerism occurs when there is restricted rotation around a double bond, usually due to steric hindrance. In this example the carbonyl group does not rotate and can either occur in the ‘up’ or ‘down’ position.
To calculate the energy minima of both molecules, the MM2 and MMFF2 force field were used. The carbonyl group orientation will change the overall energy of the molecule, but before this was experimented with, the cyclohexane ring was stabilised by changing the conformation to chair, boat and twist boat. With this, it was observed that the chair confirmation was the most stable configuration for both molecules when using both MM2 and MMFF2 methods. However it must be noted that there was only an extremely small difference (approx. 0.5 kcal/mol) between the chair and twist-boat conformers, so under normal conditions it is expected that these two conformers would interchange simultaneously. The values from both methods can be seen below:
| Molecule 9 | Molecule 9 | Molecule 10 | Molecule 10 | |
| Ring conformation | MM2 (kcal/mol) | MMFF94 (kcal/mol) | MM2 (kcal/mol) | MMFF94 (kcal/mol) |
| Chair | 49.92 | 73.98 | 43.76 | 61.28 |
| Twist-boat | 50.51 | 74.37 | 44.46 | 62.13 |
| Boat | 55.58 | 80.14 | 52.32 | 74.40 |
Using the two separate methods (MM2 and MMFF94) yielded similar energy differences between each conformation so using either method is equally reliable. It is clearly seen that the molecule 10 (with the carbonyl oxygen pointing down) is the most stable. The main reason for this is because there will steric hindrance if the carbonyl was pointing upwards with the methylene bridging group. This is not present when the oxygen points downwards in molecule 10.
When the individual components of the energies were analysed, it was observed that the torsion componenent was the major difference. Torsional energy was much higher for molecule 9 (21.87 kcal/mol) compared to molecule 10 (17.94 kcal/mol). This indicates that there is more torsional strain in molecule 9 which will arise due to the bond angles around the carbonyl group. If the bond angles lie far from the most stable 120o then the energy will be increased. For molecule 9, this angle was observed to be 118.1o, whilst for molecule 10 it was 120.5o.
During subsequent functionalisation of the alkene in both molecules, the reaction is abnormally slow. This is due to the fact that it is hyperstable[3] which means that it will be inert to hydrogenation and is primarily accredited to the large ring size in which it is situated. The alkane produced by hydrogenation is more strained than the corresponding alkene and this is normally seen in bridgehead alkenes in medium/large rings, but not for small rings which is not allowed according to Bredt’s rules[4].
Modelling Using Semi-empirical Molecular Orbital Theory
Regioselective addition of dichlorocarbene was studied. For this, the geometry was deduced and the energy of the orbitals were calculated and displayed graphically. This was done by using a quantum mechanical treatment instead of the previous classical mechanical treatment. For the following discussion, the MOPAC/PM6 MO method was used to obtain data.
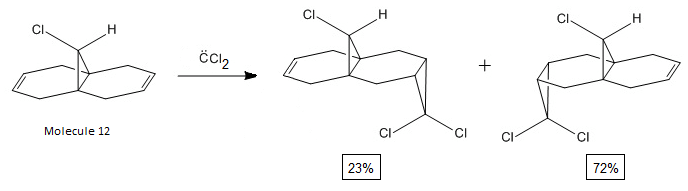
The regioselective addition of dichlorocarbene to molecule 12 is shown below and yields two products (syn:anti) of the ratio 23:72[5];
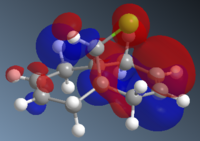
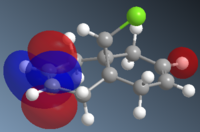
To understand the selectivity of this reaction, the molecular orbitals of molecule 12 need to be considered. The most important orbitals will be the HOMO and LUMO since it is these frontier orbitals that control the reactivity. These can be seen below:
 |
 |
 |
 |
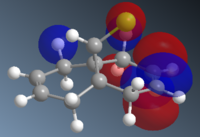 |
The molecular orbitals show that highest electron density lies around syn alkene which is seen by the HOMO. As a result, the syn alkene will be more nucleophilic and attract electrophiles more. Since diclorocarbene is an electrophile it will be more likely to attack on the syn alkene and hence give a higher more yield of the syn product.
Additionally, there is another factor that controls the regioselectivity. This arises from the interaction of the anti-alkene pi orbital (HOMO-1) and the C-Cl ᵟ* orbital (LUMO+1) which results in a lowering of the anti pi orbital energy relative to the syn-alkene pi orbital. This is known as a stabilising anti-periplanar interaction[6] and lowers the anti pi orbital by 0.08eV. This signifies that this orbital will be more thermodynamically stable and will be less reactive. Therefore, it is less nucleophilic.
After molecular optimisation using using B3LYP/6-31G(d,p) (SCAN), the absorption frequencies were for the syn and anti alkenes were calculated, along with the C-Cl stretching frequency. This was done not only for molecule 12 but a hydrogenated product (molecule A), and substituted derivatives of molecule 12. The derivatives include molecule B, C, D and E as shown below. The IR frequencies are seen in the table below:
| Compound | syn C=C / cm-1 | anti C=C / cm-1 | C-Cl / cm-1 |
|---|---|---|---|
| Molecule 12 | 1757.5 |
1737.1 |
770.80
|
| Molecuel A | 1758.1 |
- |
775.0
|
| Molecule B (C-OH) | 1757.8 |
1753.0 |
765.3
|
| Molecule C (C-CN) | 1756.5 |
1706.3 |
765.8
|
| Molecule D (C-BH2) | 1756.6 |
1657.2 |
759.0
|
| Molecule E (C-SiH3) | 1756.3 |
1690.3 |
763.8
|
The absorption frequency for the anti double bond is smaller than that of the syn double bond. This arises because of a stabilising interaction where electron density is donated from the anti alkene pi orbital to the C-Cl σ* orbital. As a result, the bond order of the anti double bond is decreased which consequently weakens the double bond; giving an overall smaller absorption frequency for the anti double bond.
The absorption frequency for the C-Cl bond in the dihydro product (molecule A) is higher than that of molecule 12. This is because there is no stabilising interaction between the two orbitals in the molecule. Thus, there is no electron dnation into the C-Cl σ* orbital therefore no decrease in bond order. This will create a stronger C-Cl bond and higher frequency. In addition, the frequencies of the syn alkene bonds in both molecule 12 and molecule A do not vary significantly indicating that there is no stabilisation interaction that includes this double bond. Hence there is no change in bond order and consequently absorption frequency.
For the OH substituent, the frequency of the anti alkene is increased which can be attributed to the donation of the lone pair of electrons from oxygen into the anti pi orbital. This will increase the alkene bond order and increase its strength which will have the increased effect on the frequency. Since the pi orbital will have more electron density, there will be donation into the C-Cl σ* orbital which will weaken the bond and therefore create a smaller C-Cl vibration frequency compared to molecule 12 and molecule A.
For molecules C, D and E the stretching frequencies are significantly lower compared to molecule 12. This is because –CN, -BH2 and SiH3 are all electron withdrawing groups where electrons will be donated into the empty p orbital on carbon, boron and silicon. The anti alkene will therefore constitute of less electron density which will lower the bond order and decrease the absorption frequency of this bond.
Structure based Mini project using DFT-based Molecular orbital methods
Stereoselective C(2)-Vinylation of 1-Substituted Imidazoles with 3-Phenyl-2-propynenitrile
The reaction below was investigated by Boris A. Trofimov et al (http://pubs.acs.org/cgi-bin/abstract.cgi/joceah/asap/abs/jo801240x.html)[7] and produces two isomers of the ratio 95:5 as seen below;
Theoretically, isomer 1 will be the major isomer primarily due to steric hindrance. When the two substituents are on the same side of the double bond, their electron clouds will overlap and therefore repel each other. This repulsion will increase the overall energy of the isomer (isomer 2) and is the reason why it has a llower yield. The mechanism for the reaction can be seen below:
The stereoselectivity of this reaction will be looked at computationally and derived, from calculations, which isomer is most stable. The method used was DTF with a base function of 6-31g. The difference in energy between the two molecules is -0.01 Hartrees with Isomer 1 being the lower energy. This is consistent with the relative percentage yield given in the above reaction scheme of a ratio of 95:5.
| molecule | ΔG/ Hartrees | Joules |
|---|---|---|
| Isomer 1 | -666.08 | -2.9038e-15 |
| Isomer 2 | -666.09 | -2.9039e-15 |
Characterisation of both isomers
Analysis of NMR data
We are interested in distingushing between the 2 stereospecific isomers. This will be done by analysing the 13C NMR and the IR specra of both isomers. Below is a table of the NMR shifts using computational methods:

| Carbon | Computational method NMR shift; E-isomer (ppm) | Computational method NMR shift; Z-isomer (ppm) |
|---|---|---|
| 1 | 74.45 | 73.41 |
| 3 | 69.83 | 69.90 |
| 5 | 56.2 | 54.84 |
| 6 | 44.11 | 45.49 |
| 7 | 60.82 | 63.68 |
| 8 | 103.48 | 103.56 |
| 9 | 82.36 | 82.78 |
| 10 | 71.75 | 69.47 |
| 11 | 71.38 | 72.03 |
| 12 | 68.48 | 68.62 |
| 13 | 72.04 | 72.22 |
| 14 | 67.99 | 67.62 |
| 16 | 160.23 | 161.08 |
The calculated NMR data for both isomers are both very similar to the literature values. This indicates that both isomers are valid and do exist. It can also be seen that carbon-13 NMR can not be used to distinguish the products
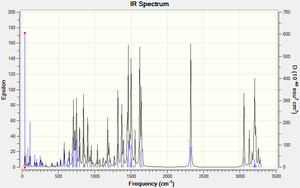
Analysis of IR data
the Ir data shows that there are no distinct differences between the two IR spectra and thuis cannot be wholly used to distinguish the two isomers to confirm with literature that the E isomer is the major product.

Optimisation files: E DOI:10042/to-6498 and Z DOI:10042/to-6499 NMR files: E DOI:10042/to-6500 and Z DOI:10042/to-6501 Frequency files: E DOI:10042/to-6502 and Z DOI:10042/to-6503
References
- ↑ Alder, K., Stein, G. Liebigs Ann. Chem. 1933
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319
- ↑ W.F. Maier, P.v.R. Schleyer., J. Am. Chem. Soc,, 1981
- ↑ Pelayo Camps, Francesc Pérez and Santiago VázquezTetrahedron,1997, 53, 9727.
- ↑ B. Halton, S.G.G. Russell, J. Org. Chem., 1991, 56,
- ↑ B. Halton, R. Boese, H.S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447.
- ↑ B. Trofimov, L. Andriyankova J. Org. Chem., 2008, 73, pg 9155