Rep:Mod:12dschubertroad

Module 1

The Hydrogenation of Cyclopentadiene Dimer

The Cyclopentadiene Dimer

The dimerisation of cyclopentadiene can adopt 2 geometries. These are the -exo and -endo forms. The reaction product can be determined by 2 forms of control, thermodynamic and kinetic. For if the reaction is under thermodynamic control then the product will be that of lowest energy. Using computer modelling we can compare the two products and their relevant energies. These two forms can be seen here with their relevant energies.

Dimer	Energy (Kcal mol-1)
-exo	31.88
-endo	34.02

From this we can see that the thermodynamic product dimer is the -exo dimer as this has the lower energy of the two (Energy difference = 2.14 Kcal mol^-1). However, the dimerisation results specifically in the -endo dimer, this can be attributed to the reaction being under kinetic control.

In order to rationalise the product choice when the reaction is under kinetic control we must consider the transition states.

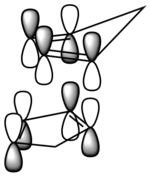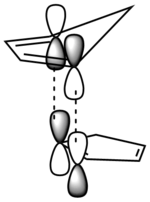
The -endo product has 4 orbital interactions in the TS	The -exo product has 2 orbital interactions in the TS

From this we can see why the -endo product is the kinetic product, as there is a better orbital interaction. This is in good agreement with the HOMO-LUMO interactions presented by Hoffmann and Woodward.

Hydrogenation of the -endo dimer

The initial hydrogenation of the -endo dimer can produce two possible products as there are two available double bonds, these can be seen below.

These two products 3 and 4 can now have their energies computed and compared in order to see which is more thermodynamically favourable.

Product	Energy (Kcal mol-1)
3	31.15
4	35.93

We can see from these calculations that the most thermodynamically stable product is product 3.

Stereochemistry of Nucleophillic additions to a pyridinium ring (NAD⁺ analogue)

Reaction 1

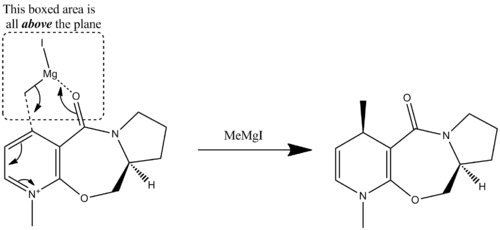
The reaction of the optically active proliniol and methyl magnesium iodide we are told proceeds with the absolute stereochemistry shown below.

An investigation into different conformers of the reactant was carried out, so that the lowest energy reactant could be obtained. Special attention was paid to adjusting the starting positions of the enol oxygen and the 5-membered ring bend (relative to the plane of the aromatic ring) before the energy optimisation was carried out.

Starting position of enol oxygen	Starting position of furthest ring carbon	Dihedral angle of carbonyl group relative to benzene ring	Energy (Kcal mol-1)
above	above	16.1o	44.57
above	below	35.0o	44.34
below	below	9.7o	43.07
below	above	7.8o	44.58

The conformer with the lowest energy can be seen below.

Prolinol

This conformer has a dihedral angle at the carbonyl of 7.8^o. By applying this fact to the mechanism by which the reaction proceeds we can see that this will always result in the methyl group being added above the plane of the molecule.

Reaction 2

Reaction 2

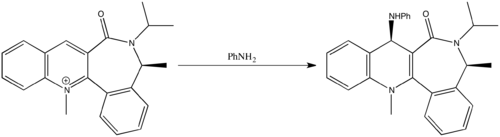
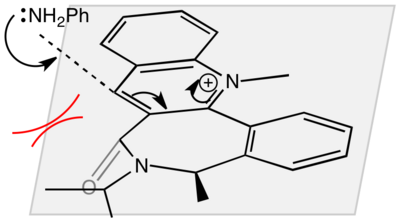
The pyridinium ring in this reaction reacts with aniline to form the product shown in the scheme to the right. As in reaction 1, the reactant was modelled on Chembio3D, and various starting geometries (in relation to the plane of the pyridine ring) were minimised using the MM2 forcefield option. The variables chosen this time were the sp³ nitrogen centre and the carbonyl group. The results of these minimisations can be seen below.

Starting position of carbonyl Group	Starting position of sp3/ Nitrogen	Dihedral angle of carbonyl group relative to benzene ring	Energy (Kcal mol-1)
above	above	26.5o	66.34
above	below	-25.3o	63.56
below	below	-22.0o	63.70
below	above	-26.2o	63.70

The most stable conformer being the one with the lowest relative energy, can be seen to the below.

This conformer has a carbonyl dihedral angle of -25.3^o, which means that it is below the plane of the pyridine ring. As we are told that the final product has the NHPh group above the plane, we can say that the mechanism involves the aniline attacking on the opposite face of the carbonyl group. This can be rationalized as occurring because the large aniline wants to avoid any steric clashes with the carbonyl group.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Proposed intermediates in Taxol synthesis

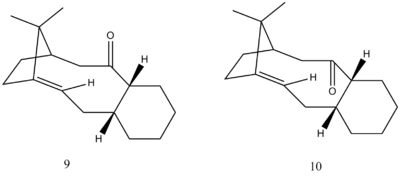
During the synthesis of Taxol, a key intermediate is proposed by Paquette to exist. This intermediate, as shown on the right, can be synthesised with the carbonyl group being either above (9) or below (10) plane. It is proposed that on standing the compound isomerises to the alternative isomer. This is an example of atropisomerism, that is hindered rotation about a single bond. The stereochemistry of the carbonyl addition will depend upon which isomer is the most stable. To calculate this, we have modelled both 9 and 10 on ChemBio3D, and minimised their energies using both the MM2 and MMFF94 force field simulations. The results can be seen in the table below.

Relative energies of isomers 9 and 10, Jmol files linked to buttons.

Isomer	Energy (Kcal mol-1)
	MM2	MMFF94
	65.52	88.17
	49.91	66.37

From this data we can see that isomer 10 has the lowest values for both the relative forcefield measurements. Note here that the cyclohexane ring in each of these appears to be in the twist-boat conformation. Minimisations were made with the cyclohexane in the lower energy chair conformation but they always either reverted to the twist boat, or minimised to a higher energy conformation. This may be due to the geometry forced on the ring from the rest of the molecule.

We are told that the subsequent functionalisation of the alkene in this reaction is abnormally slowly. This can be rationalised by the hyper-stabilisation of the alkene. According to McEwen and Schleyer, alkenes at bridgehead carbons in larger polycyclic systems are often favoured. This is because functionalisation of the double bond in the case of these large polycyclic systems causes the sp² carbon to become an sp³ which in these cases is disfavoured. This is because the sp³ carbon centres created are now conformationally of higher energy due to steric strain.

Modelling Using Semi-empirical Molecular Orbital Theory

Part 1

Compound A

The molecule to the right was created and the energy minimised using the MM2 forcefield option in ChemBio3D. The molecular orbitals were then calculated and visualised using MOPAC/RM1 methods. These molecular orbitals were then used to investigate the effects of an electrophilic attack on the molecule.

HOMO of Compound A

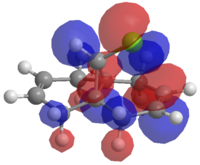
The reaction with Dichlorocarbene, can be considered to be like an electrophilic attack. Using the HOMO from the MO calculations, which is shown to the left, we can see that there is a differentiation between the two double bonds. In the HOMO the double bond on the same side as the Chlorine atom is shown to be high in electron density. From this information we can say that this double bond will be the one susceptible to electrophilic attack.

Part 2

For this we are investigating the effect that the C-Cl bond has on vibration frequencies. For this we will compare the two molecules shown below (A & B)

Using a B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation on these two molecules, we can model the IR stretching frequencies of these two molecules. These can be seen in the two plots below.

IR Spectrum of Compound A

IR Spectrum of Compound B

HOMO-2 of Compound A showing π_C=C(-exo) -> σ*_C-Cl interaction

HOMO-4 of Compound A showing p_vac-> π_C=C(-endo) interaction

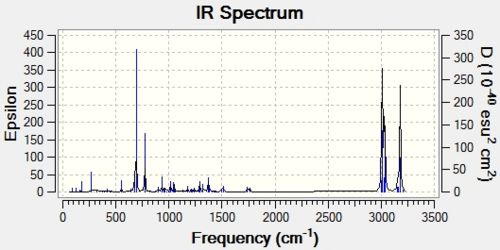
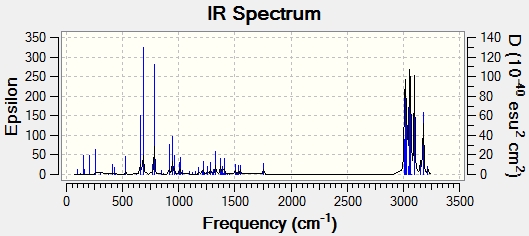
The key frequencies have been identified and tabulated below:

Molecule	Stretching Frequency (cm-1)
	C-Cl	C=C endo	C=C exo
A	772.6	1761.0	1740.8
B	782.7	1757.2	n/a

The key differences seen here are:

• a shift in C-Cl stretching frequency, the hydrogenated product has a higher stretching frequency, showing that the bond is stronger.
• a difference in the C=C stretching frequency, the -exo stretch in compound A occurs at ~20cm^-1 less than those for the -endo C=C, indicating that the -exo is weaker than the -endo double bond.

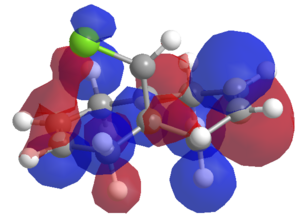
These differences can be rationalised using what was discussed earlier with reference to the electron distributions in these molecules. If we observe the HOMO-2 for the diene, then we can see that there is a constructive overlap between the -exo C=C π cloud, and the σ* C-Cl bond. This constructive overlap has acted to weaken the C-Cl bond, and thus reduces the stretching frequency of the bond.

This same reasoning can be applied to why the -exo double bond is weaker than the -endo double bond, if we observe the HOMO-4 we can see that the -endo C=C bond π cloud receives a constructive overlap from the Cl p_vac orbital. This acts to strengthen the bond. The -exo bond does not have this interaction and this is weaker, and thus has a lower stretching frequency.

Structure based Mini project using DFT-based Molecular orbital methods

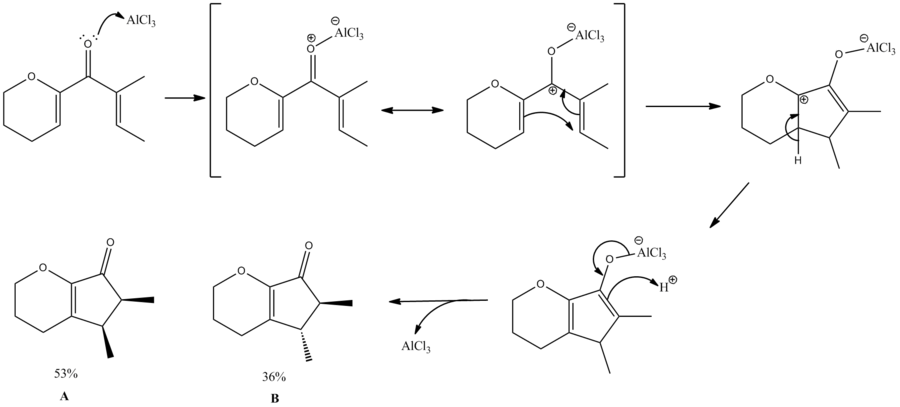
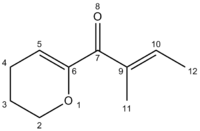
For my mini-project I decided to study the Nazarov cyclisation of (2E)-1-(3,4-dihydro-2H-pyran-6-yl)-2-methylbut-2-en-1-one as described by Liang, Gradl and Trauner.

Nazarov Cyclization of (2E)-1-(3,4-dihydro-2H-pyran-6-yl)-2-methylbut-2-en-1-one

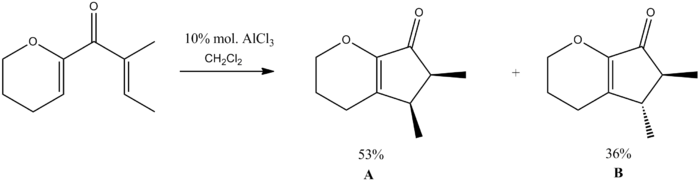
I have proposed a mechanism for this reaction as shown below.

In order to investigate the products (A & B), we first modelled them using ChemBio3D, doing some basic energy minimisations. In order to ensure the lowest energy conformation was being established many different starting positions were chosen before the minimisations. However all starting configurations of both molecules minimised to only one conformer each. This can be attributed to the small size of the molecules and therefore the lack of conformation flexibility, leading to the lowest energy conformer always being found.

Product	Energy (Kcal mol-1)
A	13.67
B	12.23

We can see that from these calculations, that B is the lower energy conformer. As the literature states that the major product of the reaction is A, we can say that this reaction is under kinetic control.

To understand this control, we can first observe the orbital interactions leading to the torqueoselectivity. This reaction is a 4π thermal cyclisation, which from orbital symmetry requirements is a conrotatory motion. Inherently, there 2 possible conrotation directions leading to torqeoselectivity in the products of this reaction, this is displayed below:

torqueoselectivity of the Nazarov cyclization.

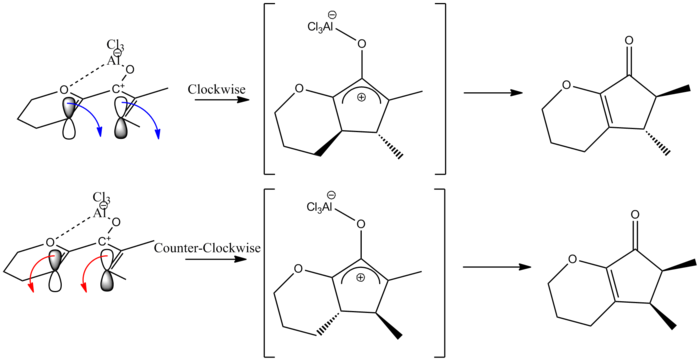
In this reaction there is a slight preference for one product (A). This can be rationalised by the presence of the ring and the oxygen on the ring. Through ring oxygen coordination (to the lewis acid) and steric strain from the ring, there is a slight preference for counter clockwise conrotation (trough more stable Transition states). This is supported by Frontiera and Collison and also Occhiato et al

NMR Calculation and Interpretation

GIAO Calculation for A (original)

GIAO Calculation for B (original)

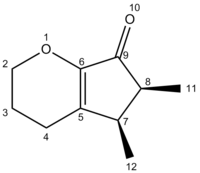
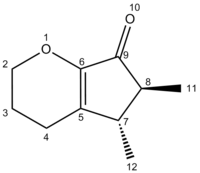
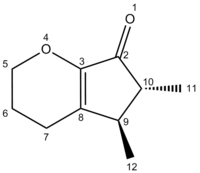
Here is a table comparing the ¹³C chemical shift values of the literature and calculated values

Product	Atom number and Shift (ppm)
	9	5	6	2	8	7	4	3	12	11
Lit A	203.27	149.70	148.69	66.81	42.13	36.06	21.97	21.66	14.79	11.22
Computed A	200.45	148.62	148.09	64.59	45.59	38.66	24.07	23.02	18.26	12.26
LitB	202.63	149.56	147.43	70.90	66.64	47.34	41.31	21.60	17.84	14.71
Computed B	200.22	148.00	147.83	64.52	48.47	43.19	24.89	22.90	18.84	16.21

Graph showing the key variations between experimental and computational changes in ¹³C shifts between A and B

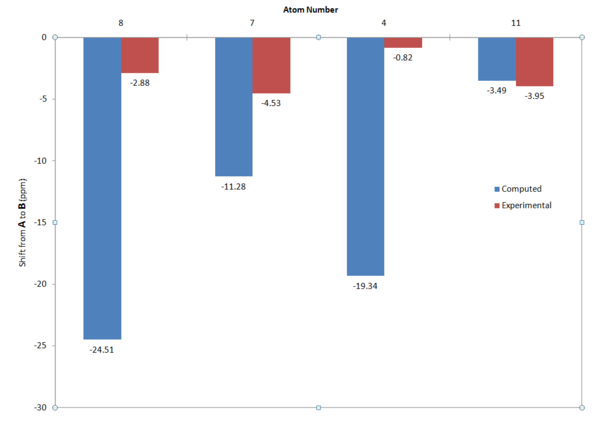
There was overall an acceptable agreement between the calculated and literature values. On this table the values where there were notable discrepancies between the calculated and literature values have been highlighted in red and amber according to their levels of disagreement. Also, highlighted in green the columns which would be used in the analysis of the products to distinguish between them. Observing these green columns we can make the following assessments:

• For Carbon 8, the literature shows this as one of the key distinguishing shifts between the products (shift of 24.5ppm). This shift is not evident in the computer calculations and is only 2.88ppm. This could perhaps be down to a poor optimisation of the product B, as the shift is missing from product B.
• For Carbon 7, the literature shows a shift of -11.3ppm. This shift is evident in the computationally modelled values, but to a lesser extent (-4.5ppm). This can again be attributed to a poor optimisation of product B.
• For Carbon 4, the literature shows a shift of 19.34ppm. For the computer calculation this shows as <1ppm shift, again poor optimisation of B.
• For Carbon 11, the literature shows a shift of 3.5ppm, and the computation shows a shift of 4.0ppm, this is in very good agreement and shows that correct optimization with respect to this carbon has occurred.

Using this information we decided to take 3 alternative approaches to trying to solve the issue. This first was to see if the issue was that the enantiomers of the products described in the literature were being produced. The second approach was to try running an alternative conformer of product through the system to see if it produced better results. The third was to model the reactants to see if unreacted product may be causing the shifts.

Enantiomers

This approach was taken; as in research into this reaction, Occhiato et al had stated that the products were the same. However in their supplementary information, they had drawn the enantiomer of B as a product.

For this investigation the enantiomers of products A and B were modelled and run through the system as before. The results are below. It must be noted that on this approach the atoms were labelled differently, however in the table they have been put in the same order for clarity.

GIAO Calculation for A (flip)

GIAO Calculation for B (flip)

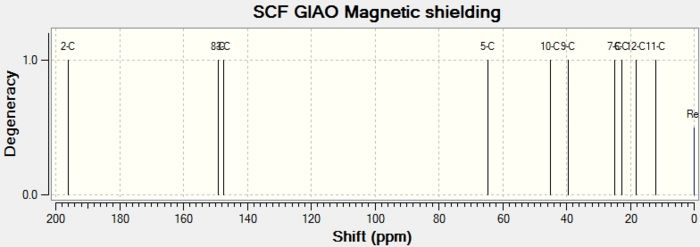
Product	Atom number and Shift (ppm)
	2	8	3	5	10	9	7	6	12	11
Lit A	203.27	149.70	148.69	66.81	42.13	36.06	21.97	21.66	14.79	11.22
Computed A'	200.32	149.154	147.434	64.62	45.04	39.54	25.01	22.70	18.15	11.91
LitB	202.63	149.56	147.43	70.90	66.64	47.34	41.31	21.60	17.84	14.71
Computed B'	199.97	148.10	147.68	64.31	48.59	41.77	23.59	22.88	18.34	15.44

This approach did not produce any better results, as the same issues with the computationally modelled B occurred.

Changing the Conformation of B

There were 2 approaches to this, the first was by separately using all the various energy minimisation techniques made available to us in this course, prior to calculating the ¹³C NMR. The second approach arose out of the fact that there was one pre-optimisation conformation of that B could be minimised to a conformer that was not the lowest energy conformation found.

After calculating the NMR for these conformations, the results were very similar to those calculated previously, with all the same discrepancies. This approach therefore is not discussed any further.

Modelling the reactant

Also stated in the research conducted by Occhiato et al was that some of the reactant (<5%) remained after the reaction. This approach was to model this reactant and calculate the ¹³C NMR. This was to see if the experimental shifts for B that do not match those seen from the computed shifts of B, could be attributed to impurity reactant present.

GIAO Calculation for Reactant

Product	Atom number and Shift (ppm)
	7	6	10	9	5	2	4	3	12	11
Computed Reactant	184.28	149.62	141.53	133.28	110.73	64.32	23.00	22.72	17.51	14.78

This data shows that were there reactant molecule present, it could be used to explain the erroneous shift of B occurring at ~65ppm. However it does not account for the other major erroneous shift at ~40ppm.

Discussion

Many methods and starting conformations were modelled for product B and all produced the same conformer that was lower energy than that of A. The literature indicated that in this reaction A was the major product (although not by a large amount). This showed that the reaction proceeded with kinetic rather than thermodynamic control, with steric and coordination factors causing A to be the kinetic product. This was in good agreement with the literature.

The products of this reaction have been differentiated using experimental ¹³C NMR. However our attempt at showing this differentiation using computational methods has not fully agreed with this. The key differences in experimental chemical shifts that differentiate the products did not show up as effectively in the computational model.

The chemical shifts calculated for product A were in good agreement with the literature quoted values and indicate that the correct conformer was modelled. However the cause of the discrepancies in this project could be attributed to a poor modelling technique for product B. Further investigation into possible other causes to these discrepancies did not fully account for them either. As no other literature ¹³13 values for product B could be found, we cannot fault the experimental technique with complete certainty. However given the reliability of the computational methods, especially on smaller molecules like those investigated; we can make indicate that perhaps the discrepancies can be attributed to errors in the original experimentation.

The computational technique did still successfully show some of the expected differences in chemical shifts, and in these cases it successfully confirmed differences between the products.

Conclusion

Computational Modelling is an extremely powerful diversely useful tool in organic synthesis. We have shown how it can be used to help rationalise why certain products are produced when a reaction is under thermodynamic or kinetic control. We have also shown how it can be used to predict spectroscopic data. These uses were shown by modelling the reactants, intermediates and the final products in certain reactions. Using these models we can asses their energies, molecular orbitals and Spectroscopic properties, and us this information in the rationalisations. As shown in the mini project, the power of computational techniques can even be used to differentiate between diasteroisomeric reaction products. In our mini project there were disagreements with the literature experimental technique. These show up the limitations of computational modelling at this level, however further investigation though repeating the laboratory experiment and higher level computing would solve this problem.