Module 3

The Cope rearrangement of 1,5-hexadiene

Here we are investigating the cope-rearrangement. This reaction is generally accepted to proceed in a concerted fashion via a chair or boat transition state.

Part 1

Part One, molecules optimised at HF/3-21G Level of theory

Matched Conformer

Structure

Symmetry

Calculated energy (Hartree)

Lit. Energy (Hartree)

anti2

C_i

-231.69254

gauche3

C₁

-231.69266

Part 2

**Part Two, Comparison of Geometries produced by B3LYP/6-31G* and HF/3-21G Levels of theory**
Basis Set & Structure	C1-C2-C3-C4 Dihedral	C1-C2 Bond Length (Å)	C2-C3 Bond Length (Å)	C3-C4 Bond Length (Å)
	-114.666^o	1.316	1.509	1.553
	-118.528^o	1.334	1.504	1.548

Part 3

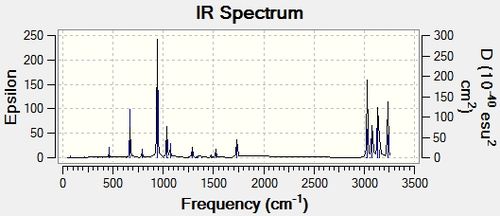
The B3LYP/6-31G* optimised structure was then sent off for Frequency analysis. The result came back with all positive frequencies, showing the optimisation was to a minima. The spectrum was also visualised. We were also able to extract various Thermochemical data from the .log file.

**Energies from Frequency Analysis (Hartrees)**
Sum of Electronic and Zero-point Energies (@0K, E=E_elec+ZPE)	Sum of Electronic and Thermal Energies (@298.25K, 1atm, E=E+E_vib+E_rot+E_trans)	Sum of Electronic and Thermal Enthalpies (H = E + RT)	Sum of Electronic and Thermal Free Energies (G = H - TS)
-234.469196	-234.461849	-234.460905	-234.500777

Optimizing the "Chair" and "Boat" Transition Structures

The Chair Transition State

An initial guess of the TS was formed using allyl fragments, these were aligned similar to the chair conformation and the terminal carbon internuclear distance between each fragment was set to 2.2Å.

Part 1 - Optimization to a TS (Berny)

Vibrationjwp108

Following the instructions we were given, this optimisation produced a successful result. The TS we had modelled had one imaginary frequency at -818cm^-1. We have animated this vibration, showing it correctly models the cope rearrangement.

Part 2 - Using the Redundant co-ordinates editor, followed by optimization to a TS (Berny)

Vibrationjwp108

Following the instructions we were given, this optimisation also produced a successful result. The TS we had modelled had one imaginary frequency at -818cm^-1. We have animated this vibration, showing it also correctly models the cope rearrangement.

The Boat Transition State

For this investigation we modelled both the reactant and product in the same mol-group, and assigned the atom numbers accordingly. We then set up a QST2 transition state optimisation which according to the script was supposed to fail. However the calculation was a success, and it correctly modelled the Chair TS. However we continued on with the project.

In order for us to get gaussian to model the boat TS, we had to change the geometry of the reactants and products, both were oriented as eclipsed for the central 4 Carbons. This was then sent off for QST2 calculation.

Vibrationjwp108

The result was a Boat TS with an imaginary frequency of -840cm^-1

Looking at both the Chair and Boat transition states we can states. We can say that the chair TS resembles the anti2 reactants and products (this was also confirmed by the unexpected success of the QST2 modelling). Whereas the Boat TS resembles the gauche reactants (the eclipsed product and reactant molecules are not to dissimilar from gauche.)

IRC Analysis

Intrinsic Reaction Coordinate analysis was used to compute the conformers of the reactants and products from the transition state. The two transition states were modeled, IRC then follows the steepest energy gradient from the TS down to a local minimum.

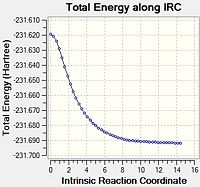
Chair

For the IRC method we were given a few options to attempt and see if they were successful. We were told that if we set the calculation to 50 steps, and to calculate the force constants once then the calculation would fail. In light of this we attempted a calculation with 75 steps, still calculating the force constants once. This also failed to reach a minimum. From this we decided to set the conditions to calculate the force constants always and take 75 steps.

The final structure of this minimisation had an energy of -231.69167 a.u. This corresponds to the Gauche 2 conformer, which on visualising the final structure of the IRC analysis we can see has been produced.

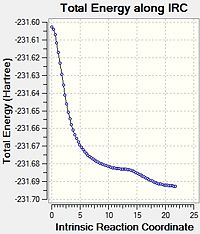
Boat

Using the result from the Chair analysis we decided to use the same method for the IRC of the boat analysis (75 steps, Calculate force constant always).

This final structure has successfully minimised to a structure with an energy of -231.69259 a.u. This is lower than that produced by the IRC from the Chair structure, but it does not appear to correlate to any of the conformers discussed in the appendix.

Increasing The Level Of Theory On Transition States

Both the Chair and Boat structures were optimised using B3LYP/6-31g* level of theory. The geometries and energies were then compared with those produced by the HF/3-21g level of theory.

**Comparison of Chair TS produced by B3LYP/6-31G* and HF/3-21G Levels of theory**
Level of theory	allyl frag. C-C-C angle (°)	allyl terminal C seperation (Å)	allyl terminal trans-H Dihedral (°)	C-C Bond (Å)	Energy (a.u)
HF/3-21G	120.5	2.02	172.3	1.39	-231.6193223
B3LYP/6-31G*	120.0	1.97	171.4	1.41	-234.55698303

**Comparison of Boat TS produced by B3LYP/6-31G* and HF/3-21G Levels of theory**
Level of theory	allyl frag. C-C-C angle (°)	allyl terminal C seperation (Å)	allyl terminal trans-H Dihedral (°)	C-C Bond (Å)	Energy (a.u)
HF/3-21G	121.7	2.14	0.0	1.38	-231.60280248
B3LYP/6-31G*	122.3	2.21	0.0	1.39	-234.54309281

Using the results from the optimisation at the B3LYP/6-31G* level of theory, we can obtain the energies of the TS at 0 and 298.15K. Using these and the anti2(lowest energy reactant conformer) energies we can calculate the activation energies and compare them to experimental values.

Comparison of the activation energy obtained at the B3LYP/6-31G* level of theory and experimental values.
	Sum of Electronic and Zero Point Energies (@0K)(a.u)	Sum of Electronic and Thermal Energies (@298.15K)(a.u)	Activation energy (@0K))(kcal/mol)	Activation energy (@298.15K))(kcal/mol)
anti2 reactant	-234.469196	-234.461849	n/a	n/a
Chair TS B3LYP/6-31G*	-234.414929	-234.409008	34.05	33.16
Experimental(Chair)(@0K)	n/a	n/a	33.5 ±0.5	n/a
Boat TS B3LYP/6-31G*	-234.402335	-234.396001	41.96	41.32
Experimental(Boat)(@0K)	n/a	n/a	44.7 ±2.0	n/a

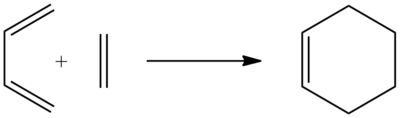
The Diels-Alder Reaction

Exercise 1, Ethene and Cis-Butadiene

Orbital interactions

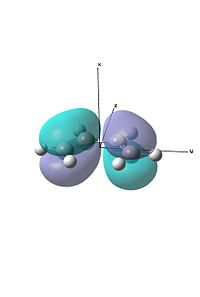
For the first exercise we were investigating a diels alder reaction between ethene and cis-bitadiene. We created both molecules and then optimised them using the semi-empirical AM1 method. Following this we visualised the HOMO and LUMO's of the two.

MO modelling for ethene and butadiene. **Note: cis-butadiene(xz plane)=ethene(xy plane)**
Species	HOMO	Symmetry of HOMO	LUMO	Symmetry of LUMO
Cis-Butadiene		Anti-Symmetric (in xz plane)		Symmetric (in xz plane)
Ethene		Symmetric (in xy plane)		Antisymmetric (in xy plane)

Due to symmetry requirements that only orbitals of the same symmetry may interact, we can see here that the HOMO of butadiene will interact with the LUMO of ethene, and the HOMO of ethene will interact with the LUMO of butadiene. Using this information we can model the Transition state of the reaction.

The Transition State

Using the information from the MO analysis, it was established that the transition state would adopt a form where one molecule sat above the other. In order to model this, a bicyclic system was created and optimised. The result then had one ethene fragment removed and the fragments separated into the reactants with the atoms returned to their original valencies. The inter fragment distance was then set to 2.2Å and the molecule was then sent for optimisation to a TS(Berny).

The result of this optimisation was successful. The transition state of the diels-alder reaction was successfully modelled, with an energy of -231.60320857 a.u. This was confirmed by the presence of an imaginary frequency at -818cm^-1, this frequency as displayed below represents the diels-alder reaction. It also shows that the bond formation is synchronous.

Vibrationjwp108

This can be compared with the lowest real frequency which is at 167cm^-1 which is the ethene rocking frequency.

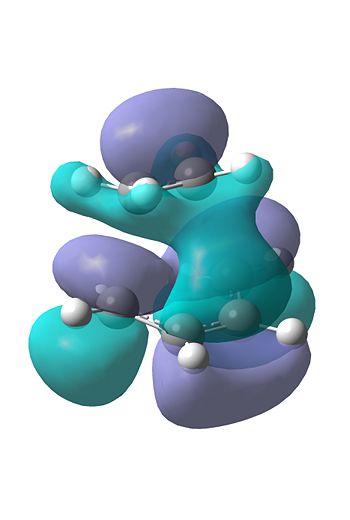
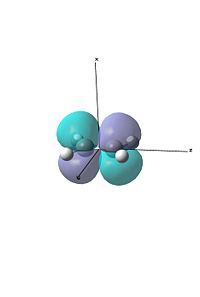
We also visualised the HOMO and LUMO for this TS. As can be seen, there is good overlap between the HOMO of ethene and the LUMO of the butadiene, forming the HOMO and LUMO. This is evident as both those fragment orbitals are symmetric, which is evident in the HOMO and LUMO of the TS, which are both also symmetric (in the σ_v plane).

Extracting the geometry from the output TS file we have formed the following table:

caption
	ethene C=C (Å)	butadiene C=C (Å)	butadiene C-C (Å)	Butadiene CCC angle	fragment separation
Reactants	1.33	1.34	1.45	125.7	n/a
TS	1.38	1.37	1.39	121.5	2.21
Typical sp² Carbon^[1]	1.34	1.34	n/a	120.0	n/a
Typical sp³ Carbon^[2]	n/a	n/a	1.54	109.5	n/a

Here we can see that the TS bond lengths are all very similar, and are intermediate between sp³ and sp² C-C bond lengths. This is indicating that in the TS the system is delocalised in nature, due to being in the transition between the two hybridisations. The interfragment distance however is much larger, at 2.2Å. This is the bond that is being formed and its length can be rationalised as being this long as it is larger than the VdW radii of the C atoms, which is 1.7Å^[3] As the bond is not yet formed.

Exercise 2, Cyclohexa-1,3-diene and Maleic Anhydride

For this investigation we were modelling the reaction between Cyclohexa-1,3-diene and Maleic Anhydride. This reaction has two possible products, the exo and endo products, as outlined below. It is known that the reaction is under kinetic control and that the endo product predominates. From this we can say that the exo transition state should be higher in energy than the endo transition state.

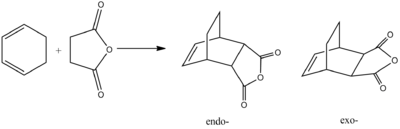
Transition State modelling

Both transition states were modelled from the initial bicyclic systems, altered, then sent for optimisation to a TS(Berny)

As shown in the below table both models produced correct Transition states, as they both correctly had 1 imaginary frequency which modelled the diels-alder reaction in question.

endo and exo transition states vibrating at the imaginary frequencies that correspond to the diels alder reaction

Transition state

Model

Corresponding imaginary Frequency

Energy of TS (a.u)

exo

Vibrationjwp108

-647cm^-1

-605.60359125

endo

Vibrationjwp108

-643cm^-1

-605.61036815

As seen here the energy of the Endo TS is lower than that of the Exo. This confirms how the reaction can be said to be under kinetic control, producing the endo product, as the endo TS is lower in energy.

geometry of TS's Analysis
Transition State	diene C=C -> C-C (Å)	Diene C-C -> C=C (Å)	Dienophile C=C -> C-C (Å)	Interfragment distance (Å)	Interfragment through space distance (dienophile carbonly Carbon - closest Carbon on diene) (Å)
exo	1.37	1.40	1.37	2.26	2.92
endo	1.37	1.40	1.37	2.23	2.85

MO Analysis

The HOMO

By visualising some of the MO's of the Transition States we can rationalise the reasoning why the endo TS is lower in energy. If we first look at the HOMO of the endo and exo, both seem to be very similar, and the similarity is confirmed by their energies aswell:

TS **HOMO** Energies
TS	HOMO Energy (a.u)
exo-	-0.323
endo	-0.324

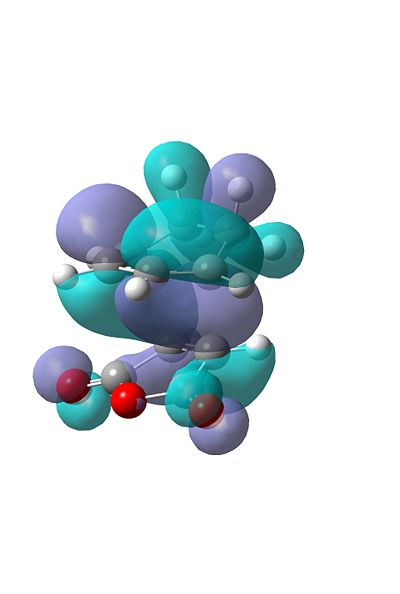
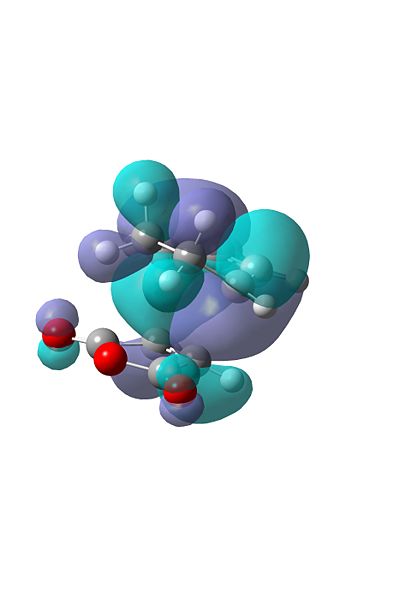
The HOMO-1

However if we visualise the HOMO-1's for both TS's this is where the secondary orbital interaction becomes evident. In the endo transition state we can see the interaction that occurs between the diene π system and the carbonyl's on the dienophile. This interaction is not present in the exo TS. This effecct is also evident in the relative energies of the HOMO-1's, as the endo, with the secondary orbital overlap is much lower in energy.

TS **HOMO-1** Energies
TS	HOMO-1 Energy (a.u)
exo-	-0.355
endo	-0.362

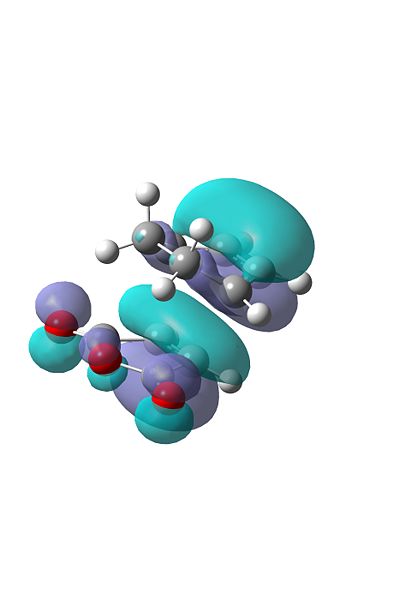
Conclusion

Using computational methods to analyse transition states ahas proven to be a successful method. We have investigated the many different methods of how the TS can be modelled. We have also done investigations from the Transition state to products using IRC analysis. Using this and MO analysis of transition states, we have been able to analyse why kinetic control of reactions produces certain products.

However in this short investigation we have only begun to investigate the potential of computational chemistry and the modelling of transition states. There are much more interactions that could've been investigated, such as solvent effects that may dramatically change the relative energies of two transition state pathways. However investigations into these would be well beyond the scope of this laboratory course.

References

↑ P. Pyykkö, M. Atsumi, Chemistry: A European Journal, 15, 2009, pp186–197 DOI:10.1002/chem.200800987
↑ P. Pyykkö, M. Atsumi, Chemistry: A European Journal, 15, 2009, pp12770–12779 DOI:10.1002/chem.200901472
↑ A.Bondi, J. Phys. Chem, 68, (3), 1964, pp441–51 DOI:10.1021/j100785a001

[1] P. Pyykkö, M. Atsumi, Chemistry: A European Journal, 15, 2009, pp186–197 DOI:10.1002/chem.200800987

[2] P. Pyykkö, M. Atsumi, Chemistry: A European Journal, 15, 2009, pp12770–12779 DOI:10.1002/chem.200901472

[3] A.Bondi, J. Phys. Chem, 68, (3), 1964, pp441–51 DOI:10.1021/j100785a001

[1]

[2]

[3]