Y3C Physical Module

Submitted by William Lim

The Cope Rearrangement Tutorial

Optimizing the Reactants and Products

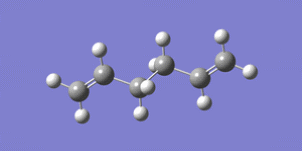
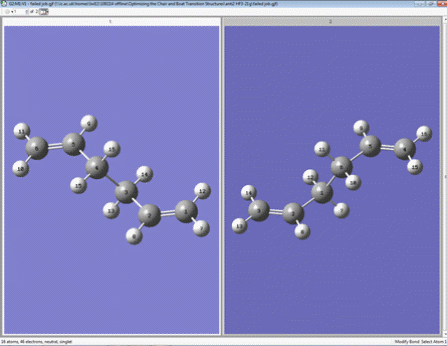
a) A molecule of 1,5-hexadiene with an anti-periplanar conformation for the central four C atoms was drawn. This was 'cleaned' and then optimized at the HF/3-21G level of theory.

The energy of the result was -231.69254 a.u..

The molecule had symmetry. Its point group was Ci.

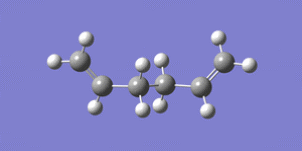
b) Another molecule of 1,5-hexadiene with a gauche conformation for the central four C atoms was drawn. It was then ‘cleaned’ and then optimized at the HF/3-21G level of theory. This structure was expected to have a higher energy than the anti structure I had just optimized.

The energy of the structure for b) was -231.69153 a.u.. This was 0.00101 a.u. higher than the molecule drawn for a) and this result was expected.

The molecule had symmetry. Its point group was C2.

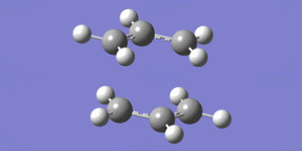
c) A molecule of 1,5-hexadiene with an anti conformation for all C atoms was drawn. This was predicted to be the lowest energy conformation. It was then ‘cleaned’ and then optimized at the HF/3-21G level of theory.

The energy of the structure for c) was -231.69260 a.u.. The molecule had symmetry. Its point group was C2.This molecule has a lower energy than a) and this was expected.

d) The molecule shown in c) was anti1 in Appendix 1. The molecule shown in b) was gauche4 in Appendix 1.The molecule shown in a) was anti2 in Appendix 1.

e) anti2 was already located and is the molecule shown in a). It has the same energy as the molecule shown in the table in Appendix 1.

f) The optimized molecule in a) was reoptimized at the B3LYP/6-31G* level. The energy of the reoptimized molecule was -234.61171 a.u.. This is a lower energy than the energy obtained by using the HF/3-21G level of theory. The overall geometry does not change. The point group is still Ci.

g) Starting from the optimized B3LYP/6-31G* structure f), a frequency calculation was run at the same level of theory.

Sum of electronic and zero-point Energies=           -234.469204

Sum of electronic and thermal Energies=              -234.461857

Sum of electronic and thermal Enthalpies=            -234.460913

Sum of electronic and thermal Free Energies=         -234.500777

Optimizing the "Chair" and "Boat" Transition Structures

The HF/3-21G level of theory was used for parts b) to f).

a) An allyl fragment was drawn and optimized at the HF/3-21G level of theory.

A new MolGroup was created and the optimized allyl structure from the first calculation was pasted twice into the new window by selecting Paste and then Append Molecule. The two fragments were then oriented so that they look roughly like the C2h chair transition state shown in Appendix 2. The terminal ends of the allyl fragments were set approximately 2.2 Å apart

This was saved as the chair_ts_guess input file.

b) A new MolGroup was created and then chair_ts_guess was pasted into the window. The structure shown in a) was then optimized for a transition state. The following settings were used:

Job Type: Opt+Freq

Optimization to a TS (Berny)

Calculate force constants: Once

Opt=NoEigen was added to the Additional keyword box at the bottom

The frequency calculation gave an imaginary frequency of magnitude 818 cm-1.

The vibration was animated to ensure that it was the one corresponding to the Cope rearrangement.

c) chair_ts_guess was also optimized using the frozen coordinate method. A new MolGroup was created and chair_ts_guess was pasted into the window. The Redundant Coord Editor from the Edit menu was then used. A new coordinate was generated and two terminal carbons from the allyl fragments which form/break a bond during the rearrangement were selected, and Bond and Freeze Coordinate were selected. This was done for the other two terminal C atoms. The following settings were then used to optimize this structure:

Job Type: Opt+Freq

Optimization to a Minimum

d) The chk file for c) was opened. The bond forming/breaking distances were then optimized by using the Redundant Coord Editor, creating a new coordinate, selecting two terminal atoms, and choosing Bond and Derivative. This procedure was repeated for the other bond. This time a transition state optimization was set up but the ‘calculate the force constants’ option was set as Never. The chk file showed an error and the log file was subsequently used. The bond forming/bond breaking bond lengths for the two pairs of terminal C atoms had increased slightly and were more similar (see table below) and the structure was similar to the one optimized in section (b).

'	Bond length for pair 1	Bond length for pair 2
b).chk	2.02040	2.02064
d).log	2.02070	2.02069

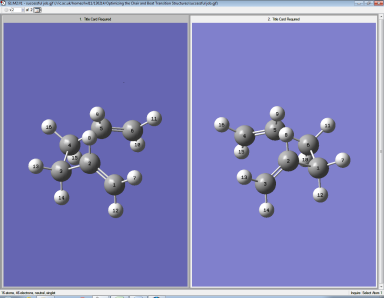
e) The boat transition structure was optimized using the QST2 method. In this method, the reactants and products for a reaction can be specified and the calculation will interpolate between the two structures to try to find the transition state between them.

One anti2 molecule (only optimized at the HF/3-21G level of theory) was added to each of the two windows made by using the File → New → Add to MolGroup function, and the atoms were labelled in the reactant and product so that each atom in the reactant is in its expected position in the product: Normal 0 false false false EN-GB X-NONE X-NONE

The first QST2 calculation was set up. Only these settings were changed from default:

Job Type: Opt+Freq

Optimize to a TS (QST2)

Since this the reactants and products looked significantly different from the real situation, the job did not give the correct result. The dihedral angle for the central C-C-C-C of the reactant and product molecule was changed to 0°. Then the C2-C3-C4 and C3-C4-C5 bonds of the reactant and product molecule were changed to 100°. QST2 calculation was done with these structures:

The result obtained was:

There was only one imaginary frequency (indicating that this was a transition state) and the vibration was animated to ensure that it was the one corresponding to the Cope rearrangement.

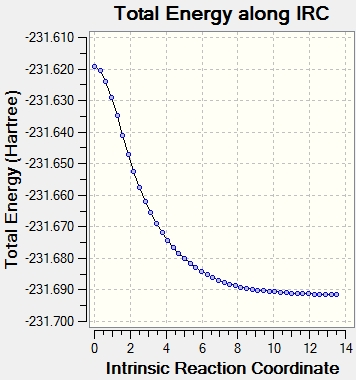
f) The optimized chair transition structure from b) was opened and the IRC method was run.

The reaction coordinate was computed in the forward direction. Force constants were calculated always, and compute more points was set to N=50.

The result gave 44 points.

This gave a product molecule with a geometry that was not optimized. Subsequently, the final point (near the minimum) was optimized using the HF/3-21G level of theory, and this gave a structure with the same energy and structure as gauche2 in Appendix 1.

g) Both the chair and boat transition structures were optimized using the B3LYP/6-31G* level of theory. The geometries were similar but the energies were significantly different. The results for the energies are shown in the tables below.

'	Electronic energy (Hartrees)	Sum of electronic and zero-point energies at 0 K (Hartrees)	Sum of electronic and thermal energies at 298.15 K (Hartrees)
Chair TS	-234.556983	-234.414929	-234.409009
Boat TS	-234.543093	-234.402342	-234.396008
Reactant (anti2)	-234.61171	-234.469204	-234.461857

'	*B3LYP/6-31G at 0 K**	*B3LYP/6-31G at 298.15 K**	Experimental at 0 K
Chair TS Activation energy (kcal/mol):	34.06	33.16	33.5 ± 0.5
Boat TS Activation energy (kcal/mol):	41.96	41.32	44.7 ± 2.0

Energies in Hartrees are converted to units of kcal/mol by multiplying the energy in Hartrees by 627.509.

The activation energies for the reaction through each transition state at 0 K is calculated by subtracting the sum of electronic and zero-point energies at 0 K of the TS by the sum of electronic and zero-point energies at 0 K of the reactant.

The activation energies for the reaction through each transition state at 0 K is calculated by subtracting the Sum of electronic and thermal energies at 298.15 K of the TS by the Sum of electronic and thermal energies at 298.15 K of the reactant.

The energies computed at 0 K are fairly close to the experimental values.

The Diels Alder Cycloaddition

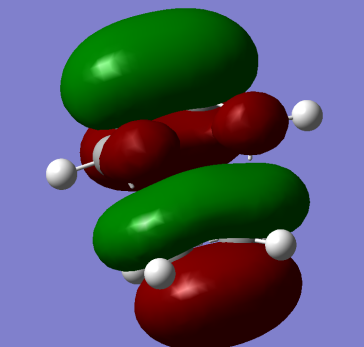
i) cis-butadiene was optimized at the HF/3-21g level of theory. The HOMO of butadiene is shown below:

It is anti-symmetric with respect to plane shown in the exercise.

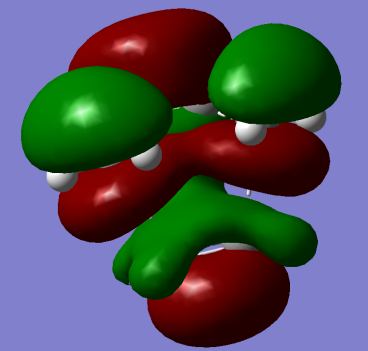
The LUMO of butadiene is shown below:

It is symmetric with respect to plane shown in the exercise.

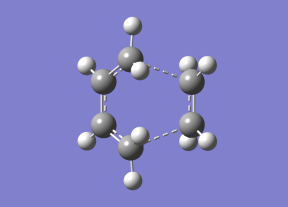
ii) The QST2 calculation was used to compute the transition state of the reaction between butadiene and ethane.

An optimized Cis-butadiene molecule (HF/3-21G level of theory) and ethene were added as the reactants and the distance between the two molecules was about 2.0 Angstroms. The product was an optimized cyclohexene molecule (HF/3-21G level of theory).The reactants were positioned together so that they looked something like the product.

After running the calculation the TS looked like this:

There was only one imaginary frequency (indicating that this was a transition state) and the vibration was animated to ensure that it was the one corresponding to the cycloaddition.

The HOMO is:

The LUMO is:

The MOs are both symmetric with respect to plane shown in the exercise.

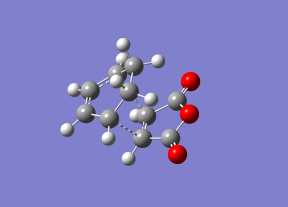
iii) The QST2 calculation was used to compute the transition state of the reaction between Cyclohexa-1,3-diene and maleic anhydride.

An optimized cyclohexa-1,3-diene molecule (HF/3-21G level of theory) and an optimized maleic anhydride molecule (HF/3-21G level of theory) were added as the reactants and the distance between the two molecules was about 2.0 Angstroms. For the 3 exo TS, the product was an optimized 3 exo molecule (HF/3-21G level of theory). For the 4 endo TS, the product was an optimized 4 endo molecule (HF/3-21G level of theory). The reactants were positioned together so that they looked something like the product.

The 3 exo TS is:

The 4 endo TS is:

There was only one imaginary frequency (indicating that this was a transition state) and the vibration was animated to ensure that it was the one corresponding to the cycloaddition.

Although the reactants and transition states were supposed to be optimized using the B3LYP/6-31G* level of theory and a frequency calculation run at the same level of theory, there was insufficient time to do this. Hence, the HF/3-21g level of theory was used.

The activation energies, and energies of the TS and reactants are shown in the tables below:

'	Electronic energy (Hartrees)	Sum of electronic and zero-point energies at 0 K (Hartrees)	Sum of electronic and thermal energies at 298.15 K (Hartrees)
exo TS	-605.6035911	-605.408138	-605.398678
endo TS	-605.6103682	-605.414906	-605.405479
Reactants	-605.6480989	-605.455833	-605.444866

'	*B3LYP/6-31G at 0 K**	*B3LYP/6-31G at 298.15 K**
exo TS Activation energy (kcal/mol):	29.93	28.98
endo TS Activation energy (kcal/mol):	25.68	24.72

The path through the endo TS is more stable than the path through the exo TS according to these energies.

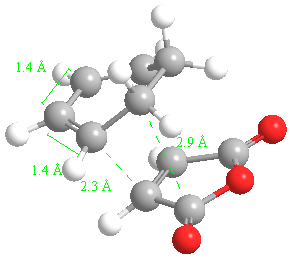
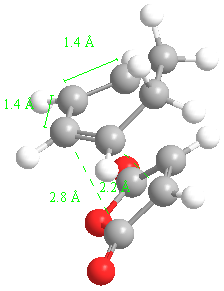
The important bond lengths for the 3 exo transition state are:

The important bond lengths for the 4 endo transition state are:

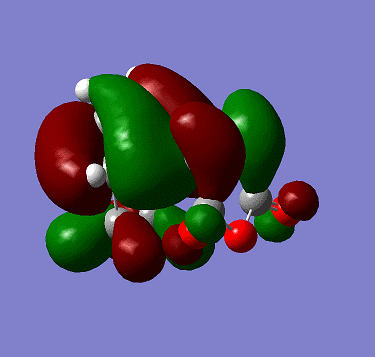
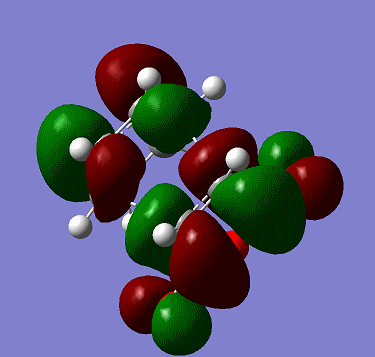
The HOMO of 3 exo is:

The LUMO of 3 exo is:

The HOMO of 4 endo is:

The LUMO of 4 endo is:

For the ethylene+cis butadiene transition structure:

Typical sp3 bond lengths are 1.54 Angstroms. Typical sp2 bond lengths are 1.36 Angstroms. The van der Waals radius of the C atom is 170 pm or 1.70 Angstroms. The partly formed sigma pi bonds in the transition state are in between these values (1.4 Angstroms).

The formation of the two bonds in the transition states are synchronous (the reactants move closer together at the same time in the animation). At the lowest positive frequency the reactants sway sideways- when one reactant moves sideways in one direction the other moves sideways in the other direction.

The HOMO at the transition state is s.

For the cyclohexa-1,3-diene+maleic anhydride reaction:

The endo form has the maleic anhydride part axial to the bicyclooctane ring whilst the exo form has the maleic anhydride part equatorial to the bicyclooctane ring. The 'secondary orbital overlap effect' favours the pathway through the endo transition state.¹

References

1. I. Fleming, in 'Frontier Orbitals and Organic Chemical Reactions', Wiley, Chichester, U.K., 1976, p. 107.