Rep:Mod:11100110101
Inorganic Computational Labs Part 1
BH3
| Summary | .log data | Structure | |||
|---|---|---|---|---|---|
 |
Item Value Threshold Converged?
Maximum Force 0.000220 0.000450 YES RMS Force 0.000106 0.000300 YES Maximum Displacement 0.000940 0.001800 YES RMS Displacement 0.000447 0.001200 YES Predicted change in Energy=-1.672479D-07 Optimization completed. |
|
| Summary | .log data | Structure | |||
|---|---|---|---|---|---|
 |
Item Value Threshold Converged?
Maximum Force 0.000204 0.000450 YES RMS Force 0.000099 0.000300 YES Maximum Displacement 0.000875 0.001800 YES RMS Displacement 0.000418 0.001200 YES Predicted change in Energy=-1.452109D-07 Optimization completed. |
|
| Summary | .log data |
|---|---|
 |
Low frequencies --- -0.9432 -0.8611 -0.0055 5.7455 11.7246 11.7625 Low frequencies --- 1162.9963 1213.1826 1213.1853 |
| Vibrations | IR-spectrum | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
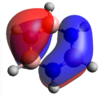
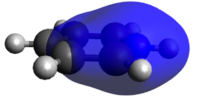
Population analysis and MO-diagram of BH3
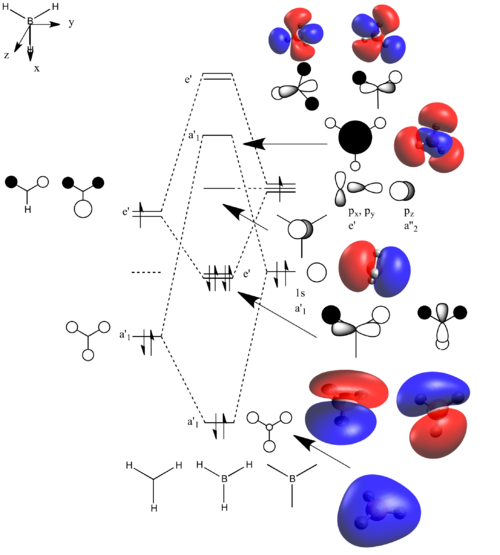
GaBr3
| Summary | .log data | Structure | |||
|---|---|---|---|---|---|
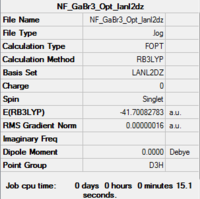 |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.282686D-12 Optimization completed. |
|
| Summary | .log data |
|---|---|
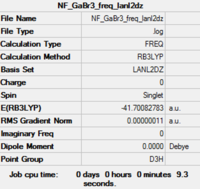 |
Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 Low frequencies --- 76.3744 76.3753 99.6982 |
| Vibrations | IR-spectrum | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
BBr3
| Summary | .log data | ||||
|---|---|---|---|---|---|
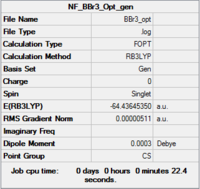 |
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000033 0.001800 YES RMS Displacement 0.000019 0.001200 YES Predicted change in Energy=-2.264035D-10 Optimization completed. |
|
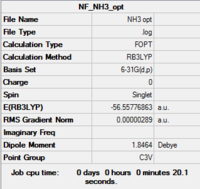
NH3
| Summary | .log data | Structure | |||
|---|---|---|---|---|---|
 |
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000010 0.001800 YES RMS Displacement 0.000007 0.001200 YES Predicted change in Energy=-7.830520D-11 Optimization completed. -- Stationary point found. |
|
| Summary | .log data |
|---|---|
 |
Low frequencies --- -10.5015 -10.4625 -0.0032 0.0270 0.1554 26.0481 Low frequencies --- 1089.6718 1694.1762 1694.1766 |
| Vibrations | IR-spectrum | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
population
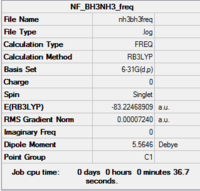
BH3NH3
| Summary | .log data | Structure | |||
|---|---|---|---|---|---|
 |
Item Value Threshold Converged? Maximum Force 0.000102 0.000450 YES RMS Force 0.000049 0.000300 YES Maximum Displacement 0.000910 0.001800 YES RMS Displacement 0.000350 0.001200 YES Predicted change in Energy=-1.975359D-07 Optimization completed. -- Stationary point found. |
|
| Summary | .log data |
|---|---|
 |
Low frequencies --- -9.3040 0.0004 0.0009 0.0013 14.5256 17.7159 Low frequencies --- 263.7488 632.1765 638.4135 |
| Vibrations | IR-spectrum | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Discussion
Geometry comparison
| Bond length | Bond Angle | |
|---|---|---|
| BH3 | 1.19 | 120 |
| GaBr3 | 2.35 | 120 |
| BBr3 | 1.93 | 120 |
Both gallium and boron are group 13 elements with three valence electrons. The trihalides of group 13 elements are hence electron deficient, they are lewis acids. Galium has a larger atomic radii, 1.36 Å, relative to boron, 0.87 Å.[1] This in itself is an important contribution to a longer Ga-Br bond length compared to B-Br.
Br has an atomic radii of 0.94 Å. BBr3 is a strong lewis acid, with the Br atoms withdrawing electron density from the centre boron. At the same time, the diffuse 4p orbitals of Br will have a poor overlap, a result of a large energy mismatch, with the lone p-orbital of the sp2 hybridized boron, leading to little back-donation. Ga and Br are in the same row however, and here the back-donation will be greater, despite of galium having more diffuse orbitals than boron, leading to a shorter than expected bond for GaBr3. As a rough example, based on atomic radii, the B-Br bond should be 1.81 Å but is in fact much longer, 1.93. The Ga-Br bond can be expected to be 2.30 Å and is calculated to be only slightly longer, 2.35 Å.
As noted above, the diffuseness of the orbitals of main group elements increases as we go down the periodic table. Hence hydrogen will have less diffuse orbitals than bromine. This is important for strong orbital-orbital interactions and strong bonding. At the same time, hydrogen lacks the p and d-orbitals of bromine, disabling any back-donation to the empty boron 2p-orbital. We have already seen above however, that back-donation from Br to B should be weak, given the diffuse nature of the bromine p-orbitals and a large energy mismatch leading to poor orbital overlap. Based on this, we can assume that the B-H bond, with good overlap between non-diffuse 1s and the sp2 hybrids, should show stronger bonding and hence shorter bond lengths compared to B-Br. This is indeed shown by calculation above, with the B-H bond having a bond length of 1.19 Å compared to 1.93 Å for B-Br. Br however is huge compared to hydrogen and hence a direct comparison is irrelevant. If we however compare the expected bond lengths based on atomic radii again, we would expect the B-H bond to be 1.40 Å (the atomic radii of hydrogen is 0.53 Å). This is evidently much longer then both the calculated (1.19 Å) and the experimentally determined (1.19 Å) bond length, indicating that there is indeed strong orbital interactions as hypothesized above. As noted earlier, these interactions are worse for BBr3 and it’s calculated bond length is longer than expected.
Finally, all angles were determined to be 120°. This justifies the common conception of the central atom of these molecules to be sp2 hybridized.
What is a bond
Defining what is a chemical is one of the most difficult questions in chemistry. In classical terms, a bond does not make sense. Moving two atoms together should simply lead to increased repulsion and the world as we know it would not exist. In quantum physical terms however, it makes more sense. By describing electrons as waves and using wave functions to solve the Schrödinger equation, we can begin to understand what a bond actually is and why it forms. Using H2+ as an example, the schrödinger equation can be rearranged into a set of different integrals. For example the overlap integral, which dictates the degree of overlap between to atomic wavefunctions but also the exchange integral. From the exchange integral, we can understand why a bond exists. In the diagram below we can see how it contributes to a lowering of the energy, giving a minima when the nuclei are at some distance r from each other. This is the source of the stabilizing effect that bring two atoms close together.[2]
So, a bond is the lowering of energy, arising from the exchange integral, when electrons occupy the space in-between two atoms in close proximity. This stabilization reaches a minima at a certain value for r and then diminishes as the atoms move away from each other. However, it only goes to zero as r goes to infinity. When is a bond a bond then?
The answer to this is that there are several types of bonds. Covalent bonds are formed by two atoms sharing two or more electrons in-between them and typically have a bond energy of 200-1000 kJ/mol. This is done by overlap of their atomic orbitals, leading to the formation of molecular orbitals. Ionic bonding does not depend on orbital-orbital interactions. Instead, they depend on simple electrostatic interactions of positively and negatively charged ions. Similar to covalent bonds, ionic bonds can be very strong with bond energies ranging between 700-4000 kJ/mol.[1]
Whilst covalent and ionic bonds spanns the strong to moderately strong bond region, dipole-dipole interactions can be much weaker. They range between 40-400 kJ/mol and occur when two polarized molecules approach each other with complementary partial charges attracted to each other.[1]
A weak form of dipole-dipole interactions has been given its own name, hydrogen bonding. This typically has a bond energy of 10-40 kJ/mol and the common example is the interactions occurring in water. A note of caution here, due to the sheer amount of hydrogen bonds in water, this fundamentally weak type of bonding collectively can become very strong.[1]
Finally, the weakest interactions are the London dispersion forces where temporary dipoles are generated instantaneously upon interactions between different molecules approaching each other. This again can be very strong if they occur in large numbers between eg. long alkyl chains.
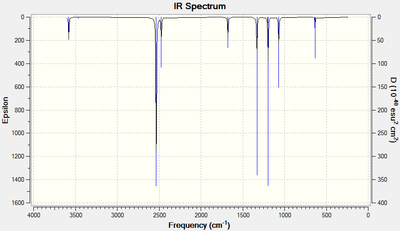
IR-analysis
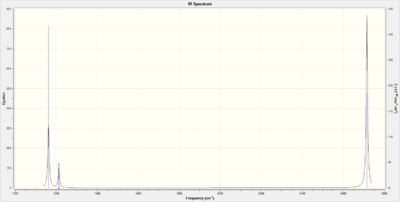
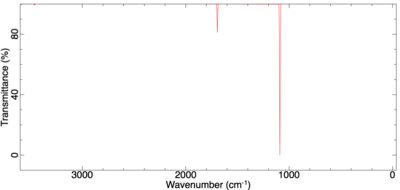
The vibrational spectrum of BH3 shows three vibrational peaks corresponding to five IR-active vibrational modes of BH3 where two pairs of vibrations are degenerate. The remaining vibration, the symmetric stretch, does not lead to a change in dipole and is hence IR-inactive.
Comparing the IR spectra of BH3 and GaBr3, we can observe that the frequencies calculated for BH3 are much greater than those calculated for GaBr3. The frequency and hence wavenumber of a vibrations is inversely proportional to the square root of the reduced mass of the atoms involved. For heavier atoms, such as Br and Ga, the reduced mass will be much greater and hence the frequency lower.
Both molecules however show the same kind of vibrations. This arise from them having the same D3h symmetry. Both have to degenerate asymmetric stretching vibrations. These have in both cases the highest wavenumber and since wavenumber can be re-written as energy it indicates that the stretching vibrations require greater energy than the bending vibrations in agreement with theory.
Ignoring the IR-inactive symmetric stretch, the ordering of the bending modes differ in-between the two molecules. In BH3 the A2" umbrella vibration is the lowest frequency bend whilst in GaBr3 it is the highest. One argument for why this is can be made by taking into account the size of the central atom. The two degenerate scissoring movements requires the bond angle to decrease from the equilibrium bond angle of 120°. In BH3, this generate a high degree of repulsion due to the short B-H bonds and the small boron center. Hence this vibration requires more energy to occur and is the most energetic of the bending modes. For GaBr3 this is not the case since its center is much larger and its bonds are longer resulting in the umbrella motion being the most energetic vibration.
Looking at the umbrella vibration itself we note that it is more intense in BH3 than in GaBr3. The intensity of a peak in an IR-spectrum will be determined by the change in dipole moment relative to the bond length. A change of dipole moment will be greater for a vibrations where the atoms involved have a large difference in electronegativity. This would argue that GaBr3 would have the most intense vibrations but this isn't the case; GaBr3 has much longer bonds and hence the intensity drops relative to BH3.[3]
Finally, looking at the force vectors of the umbrella motion we can observe a clear difference. In BH3, the light hydrogen move back and forth vigorously. In GaBr3 however, it is the central gallium atom that does. This realtes to the fact that the three hydrogens have a mass only a fraction of the central boron whilst for GaBr3, the opposite is true.
Gaussian frequency analysis
When optimizing a structure in Gaussian, we provide the program with an initial guess of what these structure might look like and its gradient. It the calculates the initial energy of the structure before it moves along the potential energy surface and then does a new energy calculation. It keeps doing this until the gradient and displacements converge within some threshold that we can determine. This will lead us to a stationary point, but we cannot know that this stationary point on the PES is a maxima or minima. The frequency analysis in gaussian computes force constants that can be used to determine vibrational frequencies. A force constant is actually a second derivative of the energy of the structure and can hence tell us if we are at a minima or maxima. [4]
The basis set that we use in our calculations must always remain the same. We can never compare two calculations if they are computed using different basis sets. If you optimize your structure using one basis set, then changing to another for the frequency calculation will change alter the potential energy surface (this will be different depending on which and how many functions we use to approximate our atomic orbitals). Thus, what used to be a minima may now be ever so slightly off.
When doing a frequency calculation of an optimized structure, we are looking for a few things. Firstly, we are interested in that all frequencies are positive. If one is negative we have a transition state and if more then one is negative, something about the structure is not correct and optimization must be remade. Secondly, we get a set of frequencies called low frequencies (see example below). The first row contains 6 frequencies relating the "6" in the 3N+6 formula for the number of vibrations in non-linear molecules. Three of these relate to translation of the molecule and these are usually extremely close to zero. The remaining three are related to rotations of the molecule and are usually greater. A rule of thumb is that these should be no greater then a few tens of wavenumbers and at least 10-100 times smaller than the frequencies calculated for the molecular vibrations. If they are not, then there are several things that can be done. For DFT calculations, we can use a finer grid used in the numerical calculations (essentially a grid with more points defining it). We can also tighten the convergence criteria by setting Opt=Tight or =VeryTight.[5]
Low frequencies --- -0.9432 -0.8611 -0.0055 5.7455 11.7246 11.7625 Low frequencies --- 1162.9963 1213.1826 1213.1853
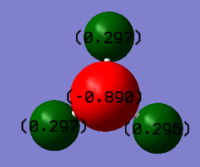
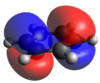
Population analysis of BH3
A population analysis of BH3 was performed using the pop=(full, nbo) keywords and the results are presented in an MO-diagram alongside the LCAOs. We can see that for the simple MOs, such as the fully bonding a'1 or the non-bonding a2" orbitals the calculations agree with the simple LCAO combinations of just two AOs. However moving to more complex MOs, such as the degenerate e' MOs the agreement between the LCAOs and the calculated MOs is worse. The general pattern can still be distinguished but since the calculations are not limited to using only two certain orbitals but use many more to find a get representation of the MO, the agreement gets worse. This tells us that qualitative MO-theory is useful for conceptual thinking but in the end we need calculations to determine the order and exact shape of the MOs.
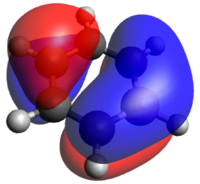
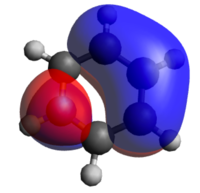
Bond strength of B-N bond in BH3NH3
The energies of BH3, NH3 and BH3NH3 are reported below. These are not rounded values and carry an error of about 0.0038 a.u. E[BH3NH3]=-83.22468915 a.u.
E[BH3]=-26.61532358 a.u.
E[NH3]=-56.55776863 a.u.
By calculating the energies of BH3, NH3 and BH3NH3 we can calculate the energy of the B-N bond. ΔE=E[BH3NH3]-(E[BH3]+E[NH3])=-83.22468915-(-26.61532358+(-)56.55776863)=-0.05159694 a.u.≈ -135.78 kJ/mol. This indicates that the B-N is a very weak bond compared to other covalent bonds and reflects the adduct nature of this molecule rather than a pure covalent bond. This is strengthened by the long B-N bond, 1.68 Å which can be compared to 1.54 Å for a typical C-C bond. [6]
Mini project - Aromaticity
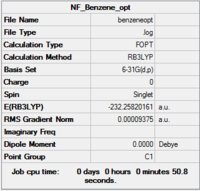
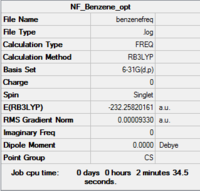
Benzene
| Summary | .log data | Structure | |||
|---|---|---|---|---|---|
 |
Item Value Threshold Converged? Maximum Force 0.000271 0.000450 YES RMS Force 0.000076 0.000300 YES Maximum Displacement 0.000744 0.001800 YES RMS Displacement 0.000237 0.001200 YES Predicted change in Energy=-2.562450D-07 Optimization completed. -- Stationary point found. |
|
| Summary | .log data |
|---|---|
 |
Low frequencies --- -18.1452 -16.1886 -8.5146 -0.0003 0.0001 0.0004 Low frequencies --- 413.9378 414.4693 620.9035 |
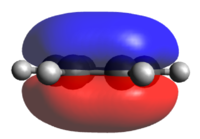
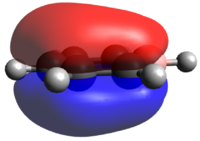
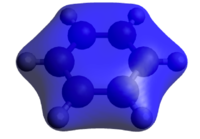
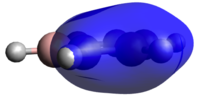
Benzene belongs to a group of molecule considered to be aromatic. Aromaticity relates to the extra stabilizing energy that we get by having 4n+2, also known as the Hückel rule, p-electrons in a fully conjugated, planar, cyclic system. Eg, based on the energy of hydrogenation of cyclohexene, 120 kJ/mol, benzene should have an energy of hydrogenation of 360 kJ/mol. However, the experimental value has been determined to be 208 kJ/mol, meaning that something is making benzene more stable than expected; this extra stabilization is called aromaticity. This stabilizing effect is often explained using molecular orbital theory by combining the 6 p-orbitals in benzene in linear combinations of atomic orbitals, LCAOs. In particular, the important molecular orbitals (MO) is the all in-phase combination of the p-orbital shown below. It renders complete charge delocalisation across the ring which is the key feature of aromaticity. The 6 π-electrons are shared between all six carbon atoms, creating a molecule with a single C-C bond length somewhere in between a typical C-C single bond and C=C double bond.
So the commonly derived all in-phase combination of p-orbitals is indeed observed in our calculations. Also observed are the two degenerate e2g MOs, both with one nodal plane and substantial delocalization. These three are the key contributors to the stabilizing energy attributed to aromaticity, containing the 4n+2=6 p-electrons available to the system.[6]
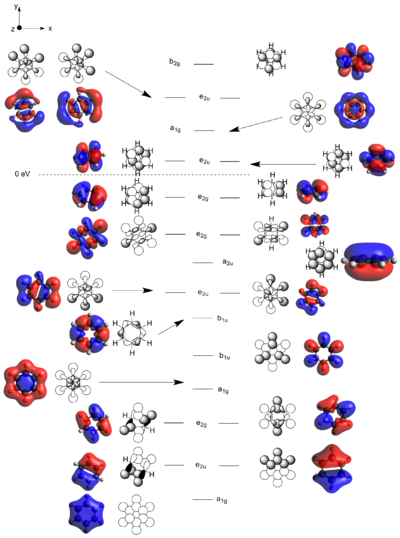
Boratabenzene
| Summary | .log data | Structure | |||
|---|---|---|---|---|---|
 |
Item Value Threshold Converged? Maximum Force 0.000000 0.000002 YES RMS Force 0.000000 0.000001 YES Maximum Displacement 0.000002 0.000006 YES RMS Displacement 0.000000 0.000004 YES Predicted change in Energy=-2.980389D-13 Optimization completed. -- Stationary point found. |
|
| Summary | .log data |
|---|---|
 |
Low frequencies --- -13.0133 0.0004 0.0005 0.0006 14.3627 17.9755 Low frequencies --- 371.3841 404.1246 565.1585 |
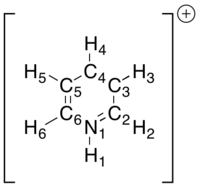
Pyridinium
| Summary | .log data | Structure | |||
|---|---|---|---|---|---|
 |
Item Value Threshold Converged? Maximum Force 0.000000 0.000002 YES RMS Force 0.000000 0.000001 YES Maximum Displacement 0.000000 0.000006 YES RMS Displacement 0.000000 0.000004 YES Predicted change in Energy=-2.871910D-14 Optimization completed. -- Stationary point found. |
|
| Summary | .log data |
|---|---|
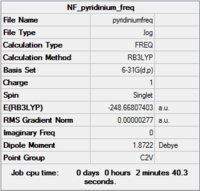 |
Low frequencies --- -5.3629 -0.0014 -0.0011 -0.0010 17.4126 18.0549 Low frequencies --- 392.4616 404.0526 620.4772 |
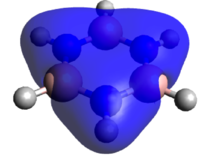
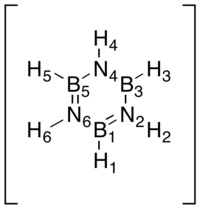
Borazine
| Summary | .log data | Structure | |||
|---|---|---|---|---|---|
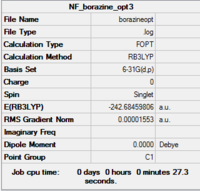 |
Item Value Threshold Converged? Maximum Force 0.000055 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000172 0.001800 YES RMS Displacement 0.000055 0.001200 YES Predicted change in Energy=-1.110138D-08 Optimization completed. -- Stationary point found. |
|
| Summary | .log data |
|---|---|
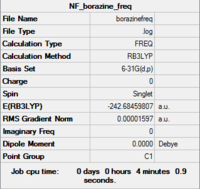 |
Low frequencies --- -11.4199 0.0005 0.0009 0.0010 7.4725 10.7144 Low frequencies --- 288.5444 290.5145 404.3239 |
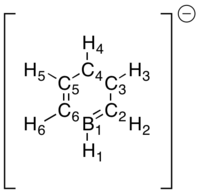
Charge distribution comparison
| Benzene | Boratabenzene | Pyridinium | Borazine | |
|---|---|---|---|---|
| Structure |  |
 |
 |
|
| Charge distribution |  |
 |
 |

|
| Charge scale |  |
 |
 |

|
| Charge atom 1 | -0.239 | 0.202 | -0.476 | 0.747 |
| Charge atom 2 | -0.239 | -0.588 | 0.071 | -1.102 |
| Charge atom 3 | -0.239 | -0.250 | -0.241 | 0.747 |
| Charge atom 4 | -0.239 | -0.340 | -0.122 | -1.102 |
| Charge atom 5 | -0.239 | -0.250 | -0.241 | 0.747 |
| Charge atom 6 | -0.239 | -0.250 | 0.071 | -1.102 |
| Charge hydrogen 1 | 0.239 | -0.096 | 0.483 | 0.077 |
| Charge hydrogen 2 | 0.239 | 0.186 | 0.285 | 0.432 |
| Charge hydrogen 3 | 0.239 | 0.179 | 0.297 | 0.077 |
| Charge hydrogen 4 | 0.239 | 0.186 | 0.292 | 0.432 |
| Charge hydrogen 5 | 0.239 | 0.179 | 0.297 | 0.077 |
| Charge hydrogen 6 | 0.239 | 0.186 | 0.285 | 0.432 |
| DOI | DOI:10042/31331 | DOI:10042/31317 | DOI:10042/31314 | DOI:10042/31327 |
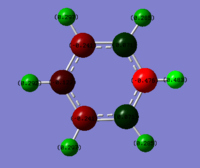
The charge distribution for benzene is, given its high D6h symmetry, very simple. The more electronegative carbon has a slightly higher electron density, i.e. negative charge, than its neighboring proton. By exchanging one C-H unit for a B-H and adding one negative charge, we get boratazene. This is a common ligand, acting very much like the aromatic cyclopentadienyl anion. It has a lower symmetry, C2h, and with boron being even less electronegative than carbon, the ring carbons all have a more negative partial charge than in benzene and the boron has large positive charge. Similarly, all ring protons but the B-H proton have a less positive, more negative partial charge than in benzene. This indicates that by withdrawing electron density from the boron onto the carbons, on whom the overall negative charge resides rather than in the empty p-orbital of boron, the pi-orbital system is distorted so that a larger proportion of electron density is carried by the protons. The B-H proton however, having a similar electronegativity as boron, is almost uncharged.
The pyridinium cation replaces the B-H of boratabenzene with an N-H unit and a positive rather than a negative charge. Although the positive charge is commonly placed on the nitrogen atom, the partial charges clearly show that this is not a realistic description. On the contrary, the nitrogen bears a large negative charge at the expense of the added N-H proton which bears a large positive charge. Unlike in benzene, C2 and C6 carry small but yet positive charges, a result of the electron-withdrawing properties of the neighboring nitrogen. C3 and C5 however are negatively charged which can be rationalized by a more distant relationship with the nitrogen but also that they benefit from a resonance effect in which the well-disguised enamine character of pyridine is shown. Finally and barely surprising, the C-H hydrogens all have a greater positive partial charge than the hydrogens in benzene as the electron density is withdrawn into the π-system.
Finally, borazine stands out relative to the other three examples discussed. Beginning with the B-H hydrogens, they show only a very small positive charge as seen in boratabenzene. The N-H hydrogens on the other hand carry a much larger positive charge, in agreement with the charge carried by the N-H hydrogen in the pyridinium cation. The character of the hydrogens are hence not surprising and confirms what we have seen above. However the ring framework is very different. The bonds are of equal length but slightly longer than those observed for benzene (calc. bond lengths 1.43 Å vs 1.40 Å for benzene). This would indicate that the double-bond character is reduced. This is indeed confirmed by observing the partial charges where large negative charges reside on nitrogens and large positive charges on boron. Hence a reasonable resonance form of the structure as drawn above would be one with alternating positive and negative charges, lacking double-bonds.
MO-comparison
Three MOs of the four molecules that have been discussed above were selected for analysis. The selected MOs depict the π-system of each molecule and is hence relevant for a discussion regarding aromaticity.
The case with all p-orbitals in-phase are all very similar, however with some distinctive modifications. Benzene, given its symmetry, naturally has a completely symmetric MO. Boratabenzene sees a skewed electron-density away from the boron atom and onto the ring carbons in agreement the the charge distribution analysis above. The pyridinium molecule see the exact opposite happening with electron-density being skewed towards the ring nitrogen. Finally, borazine has a C3 symmetric MO distorted towards the three nitrogens and away from the three boron atoms as would be expected. The energy for borazine is also very similar to that of benzene, -9.833 eV versus -9.797 eV for benzene, highlighting the similarities between the two and somewhat justifying borazine's nickname "the inorganic benzene". However, it has to be noted, as in the charge analysis above, that the charge is much more localized in borazine. That would reduce the aromatic stability hence indicating that the similar energies must be achieved through some other favorable interaction in borazine. This interaction is likely a strong ionic contribution to the wavefunction.
Borataborazine and the pyridinium molecule however differ a lot when comparing energies. Borataborazine's all in-phase MO has an energy of -3.595 eV, indicating that replacing a C-H unit with a B-H results in a large destabilization. In contrast, the pyridinium MO appears much more stable than any of the other molecules with an energy of -17.432 eV.
Where do these differences in aromaticity arise from? One argument is that the p-orbital involved in the π-system from the nitrogen and the boron respectively have different energies relative to the p-orbital of carbon. A good reference for such energies are valence-orbital ionization energies which for boron, carbon and nitrogen are -8.3 eV, -10.6 eV and -13.2 eV respectively. (CITE Gray and DeKock) This can be rationalized by the increasing electronegativity as you go from left to right in a row. Nitrogen's p-orbital hence is deeper, more negative, in energy and hence significantly lowers the energy of the entire π-system. Conversely, boron has a high lying p-orbital, increasing the energy of the π-system.


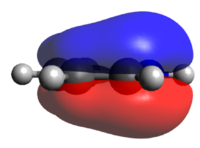
If we now study the second row of MOs shown above, we can easily see that they arise from p-orbital overlaps as shown to the right. For benzene and borazine, the entire degenerate pair is shown for completeness. The benzene orbitals are highly symmetric with the electron density delocalized evenly in both orbitals. Borazine also has two degenerate orbitals. They have a negative, stabilizing energy and it is hence logical that the electrons clouds are skewed towards the more electronegative nitrogen atoms. Looking at boratabenzene and pyridinium, there are no degenerate orbitals due to the lower symmetry (C2v). The two degenerate orbitals hence are split and the MOs relating to the p-orbital arrangement shown right are shown above. For boratabenzene, the MO shown above has clear anti bonding characteristics with a large density skewed onto the boron. For pyridinium, clear bonding characteristics can be observed with a large electron-density skewed onto the electronegative nitrogen. This also explains why the boratabenzene MO is HOMO-21 whilst that of pyridinium is HOMO-20. In other words, of the initially degenerate pair, the shown orbital for boratabenzene became the "anti-bonding" and that of pyridinium became the bonding has the degeneracy split.
Finally, looking at the last row of MOs in the table above, we can see that they arise from the all in-phase 2s atomic orbitals. This is clear in the symmetric case of benzene and in the less symmetric case of pyridinium where the electronegative nitrogen pulls electron density towards it. The pyridinium orbital is also lower in energy relative to the benzene MO due to a lower-lying nitrogen 2s-orbital which lowers the energy of the σ-system. Observing the boratabenzene orbital however, we see something very different. The carbon 2s orbitals still form a σ-system but this excludes the boron. This is due to the boron 2s orbital being too high in energy and it interacts with the carbon 2p orbitals rather than with carbon 2s (See diagram to the right). Similarly, the borazine σ-system only includes the nitrogen 2s orbitals.
References
- ↑ 1.0 1.1 1.2 1.3 Shriver and Atkins' Inorganic Chemistry, Atkins, P., Overton, T., Rourke, J., Weller, M., Armstrong, F., Oxford University Press, 2009
- ↑ Physical Chemistry: A molecular apporach, McQuarrie, D. A., Simon, J. D., University Science Press, 1997
- ↑ Infrared spectrum: Interpretation, Chemwiki, University of California Davis http://chemwiki.ucdavis.edu/Physical_Chemistry/Spectroscopy/Vibrational_Spectroscopy/Infrared_Spectroscopy/Infrared%3A_Interpretation, Accessed 21-10-2014
- ↑ Lecture notes from Quantum Mechanics 3, Bearpark, Imperial College London, M., 2014
- ↑ Vibrational analysis in Gaussian, Joseph W. Ochterski, http://www.gaussian.com/g_whitepap/vib.htm, accessed 20-10-2014
- ↑ 6.0 6.1 Organic chemistry, Clayden, J., Warren, S., Greeves, N., Oxford University Press, 2012