Rep:Mod:1101927
Computational lab - module 1 organic
Modeling using molecular mechanics
The Hydrogenation of Cyclopentadiene
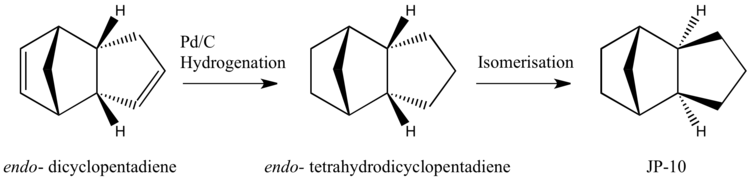
Exo-tetrahydrodicyclopentadiene is a high performance single-component fuel, known as JP-10. It has found application as a jet fuel, used in aircrafts and missiles [1], having several desirable properties such as high thermal stability, high energy density and low cost[2]. Industrially, it is made from the isomerisation of endo-tetrahydrodicyclopentadiene, which is in turn made from the hydrogenation of endo-dicyclopentadiene, typically with a Pd/C catalyst [3] [4] (Scheme 1.). Endo-dicyclopentadiene is the product of the Diels Alder π4s + π2s cycloaddition between two molecules of cyclopentadiene. The reactions involved in this process, notably the dimeristion of cyclopentadiene and the hydrogenation of dicyclopentadiene, (Scheme 2. and 4.) show pronounced stereo- and regio- control. It is the intention to use molecular mechanics to model the products of these two reactions in an attempt to rationalise their stereo- and regio-chemical outcomes.
Part 1. Dimerisation of cyclopentadiene
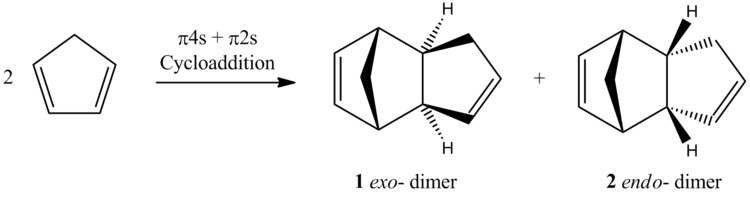
Cyclopentadiene undergoes a π4s + π2s cycloaddition to dicyclopentadiene. This reaction has two potential products, the exo- isomer (1) and the endo- isomer (2), shown in Scheme 2 (relative sterochemistry). However, only formation of the endo- isomer is observed.
The selectivity of a reaction may be guided by kinetic of thermodynamic control. Kinetically controlled reactions are generally irreversible under the reaction conditions and the observed major product is that with the lowest barrier to formation. In other words, the outcome is determined by the stability of the transition state rather than the stability of the product. Thermodynamically controlled reactions are reversible under the reaction conditions resulting in an equilibrium. Therefore, the outcome of a thermodynamically controlled reaction is determine by the stability of the products. Molecular mechanics may be used to find the relative energies of 1 and 2. Depending on whether the endo- isomer (2) is higher or lower in energy, one can determine whether the reaction is under thermodynamic or kinetic control.

| energies (kcal/mol) | energy difference (kcal/mol) | ||
|---|---|---|---|
| 1 | 2 | ||
| Stretch | 1.2850 | 1.2508 | 0.0342 |
| Bend | 20.5805 | 20.8477 | -0.2672 |
| Stretch-Bend | -0.8380 | -0.8358 | -0.0022 |
| Torsion | 7.6555 | 9.5109 | -1.8554 |
| Non-1,4 VDW | -1.4174 | -1.5440 | 0.1266 |
| 1,4 VDW | 4.2333 | 4.3202 | -0.0869 |
| Dipole/Dipole | 0.3775 | 0.4477 | -0.0702 |
| Total Energy | 31.8764 | 33.9975 | -2.1211 |
Models of dimers 1 and 2 were constructed in ChemBio3D ultra. Geometry minimisation was performed on both molecules using the MM2 force field. The results of both calculations can be seen in Table 1 (click on molecule numbers for Jmol).
The calculations found the exo-product (1) to be the lowest energy isomer of the two by ≈2.1 kcal/mol. However, this is not the observed product of the dimerisation of cyclopentadiene. Therefore, one can conclude that the reaction is not under thermodynamic control, but rather kinetic control. This can be rationalised by the additional orbital overlap of the frontier molecular orbitals on formation of 2, stabilising the transition state (Scheme 3.). Further calculations could test this prediction by calculating both transition states by density function theory.
Part 2. Hydrogenation
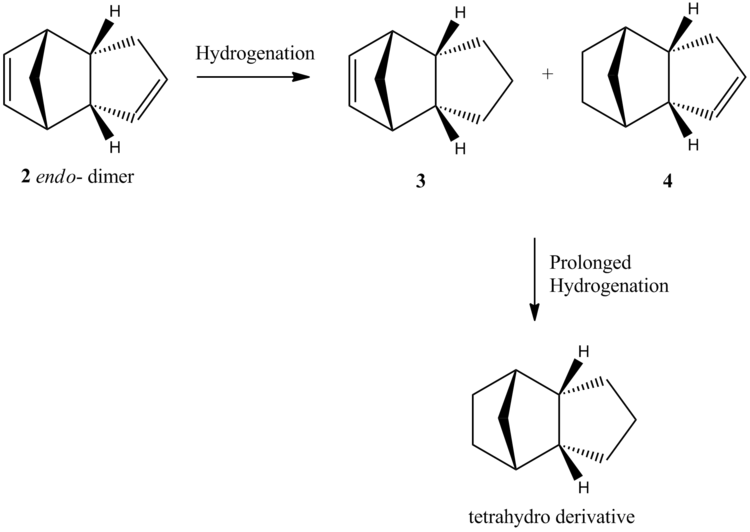
The product (2) of the dimerisation undergoes hydrogenation to initially give only one of the two dihydro derivatives, 3 and 4, as shown is Scheme 4. After prolonged hydrogenation this eventually gives the tetrahydro derivative. Again, molecular mechanics can be used to calculate the relative energies of 3 and 4. By analysing the relative contributions to the total energy of each molecule, one can attempt to rationalise their relative stabilities and use this to predict which of the two molecules is formed.
| energies (kcal/mol) | energy difference (kcal/mol) | ||
|---|---|---|---|
| 3 | 4 | ||
| Stretch | 1.2349 | 1.0964 | 0.1385 |
| Bend | 18.9384 | 14.5246 | 4.4138 |
| Stretch-Bend | -0.7609 | -0.5494 | -0.2115 |
| Torsion | 12.1240 | 12.4973 | -0.3733 |
| Non-1,4 VDW | -1.5017 | -1.0702 | -0.4315 |
| 1,4 VDW | 5.7289 | 4.5127 | 1.2162 |
| Dipole/Dipole | 0.1631 | 0.1406 | 0.0225 |
| Total Energy | 35.9266 | 31.1520 | 4.7746 |
Models of dimers 3 and 4 were constructed in ChemBio3D ultra. Geometry minimisation was performed on both molecules using the MM2 force field. The results of both calculations can be seen in Table 2.
The calculation showed that molecule 4, with the remaining double bond on the endo-ring, is lowest in energy by ≈4.8 kcal/mol. The largest contributing factor to the difference in stability is the Bend term, which is 4.4 kcal/mol higher for 3 than 4. This term alone almost accounts for the difference in energy entirely and corresponds to strain arising from non-ideal molecular angles.
Examination of the detailed MM2 reports show that the largest contributors to the bend energy in both 3 and 4 are the C-C-C bond angles associated with the unsaturated components of the 5 membered rings. This is because the angles are closer to ideality for the sp3 carbon centres (ideal = 109.5°) present in the saturated rings, than the sp2 carbon centres (ideal = 120°) in the unsaturated rings. The difference between 3 and 4 is that the reduced bond angle across the bridging carbon has the effect of squeezing and reducing the opposite bond angles in the corresponding 5-membered ring. This means the angles across the double bond in 3 are even further from ideality than those across the double bond in 4, which is why 3 is the higher energy mono unsaturated derivative.
Kinetic and mechanistic studies [5] have shown that compound 3 is simply not formed. This would appear to agree with the results from the MM2 calculations. However, this is because hydrogenation of the alkene to give 3 is found to have a much higher barrier to formation then hydrogenation of the alkene to give 4. In other words, even though compound 4 is more stable, the reaction is still under kinetic control. This explains why 4 is formed quickly, but the tetrahedro derivative is only formed after prolonged hydrogenation.
Stereochemistry of a proposed synthetic intermediate towards the synthesis of taxanes
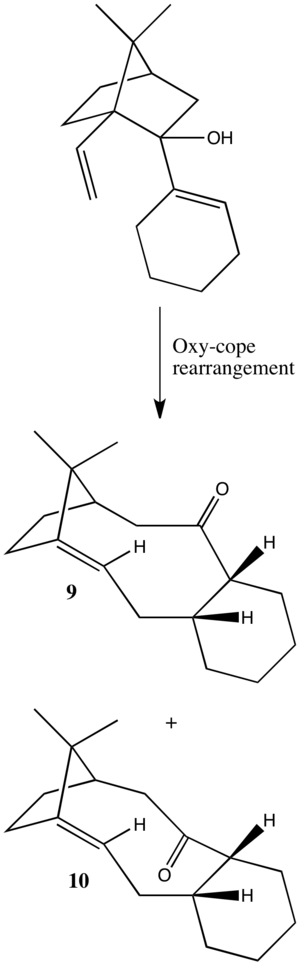
The reaction, as shown in Scheme 6., is an atropselective oxyanionic Cope rearrangement reported by Paquette[1]. Products of this reaction have been proposed as synthetic analogues and potential intermediates towards the synthesis of taxanes [2], a class of diterpenoids isolated from the Taxus (Yew) genus. Perhaps the most well known example in this family of natural products is Taxol, originally isolated from the bark of the pacific yew tree[3], that has become a commercially and clinically successful anti-cancer drug.
The reaction, as shown in Scheme 6., constitutes the key step in a construction of the fused cyclic framework that forms the basic carbon skeleton of the majority of taxanes. Several studies have been published that attempt to incorporate the functionality required for application of this scheme to the total synthesis of Taxol[4][5] and Taxusin[6]. However, a complete total synthesis utilising this strategy has not yet been reported.
Part 1.
Products of the oxyanionic Cope rearrangement such as those shown in Scheme 6., or substituted derivatives, are initially formed with the carbonyl group either facing upwards (9) or downwards (10). One standing this converts to the alternative atropisomer. As this process is under thermodynamic control, molecular mechanics may be used to determine the relative energies to find the most stable atropisomer.
Models of 9 and 10 were constructed in ChemBio3D and minimised using both the MM2 and MMFF94 force fields. The results of these calculations can be seen in tables 3 and 4.
| energies (kcal/mol) | energy difference (kcal/mol) | energies (kcal/mol) | energy difference (kcal/mol) | |||
|---|---|---|---|---|---|---|
| 9 | 9' | 10 | 10' | |||
| Stretch | 2.7848 | 3.3221 | -0.5373 | 2.6204 | 3.3096 | -0.6892 |
| Bend | 16.5415 | 20.4884 | -3.9469 | 11.3388 | 16.8295 | -5.4907 |
| Stretch-Bend | 0.4305 | 0.4980 | -0.0675 | 0.3432 | 0.4352 | -0.0920 |
| Torsion | 18.2507 | 22.0138 | -3.7631 | 19.6719 | 20.1054 | -0.4335 |
| Non-1,4 VDW | -1.5524 | -1.0696 | -0.4828 | -2.1613 | -0.1289 | -2.0324 |
| 1,4 VDW | 13.1093 | 14.9656 | -1.8563 | 12.8721 | 13.7744 | -0.9023 |
| Dipole/Dipole | -1.7248 | -1.8326 | 0.1078 | -2.0023 | -1.7834 | -0.2189 |
| Total Energy | 47.8395 | 58.3856 | -10.5461 | 42.6828 | 52.5418 | -9.8590 |
| energies (kcal/mol) | energy difference (kcal/mol) | energies (kcal/mol) | energy difference (kcal/mol) | |||
|---|---|---|---|---|---|---|
| 9 | 9' | 10 | 10' | |||
| Total Energy | 70.5284 | 82.6200 | -12.0916 | 66.2783 | 74.7125 | -8.4342 |
| Total energies (kcal/mol) | energy difference (kcal/mol) | ||
|---|---|---|---|
| 9 | 10 | ||
| MM2 | 47.8395 | 42.6828 | 5.1567 |
| MMFF94 | 70.5284 | 66.2783 | 4.2501 |
The energy minimisation by MM2 and MMFF94 force field revealed that anitropisomer 10, with the ketone facing downwards was more stable by 5.1567 and 4.2501 kcal/mol respectively, as summarised in Table 5. Therefore, one would expect, given thermally equilibrating conditions, for 9 to eventually convert to 10. The fused cyclohexane ring was found to adopt the chair conformation in both atropisomers. However, it was noticed on comparison of the structures, that 9 and 10 had opposite chair conformations. This can be visualised in Jmol (click links in tables 3 or 4). Given this, each antropisomer was modelled with the alternative chair conformation (9' and 10'). These were found to be higher in energy by approximately 10 kcal/mol for both methods. What this shows is that in order for one antropisomer to convert to the lowest energy conformation of the other, the cyclohexane ring must ring flip to the alternative chair. This would be difficult since the cyclohexane ring is highly restricted by its fused nature and this may explain why atropisomerism is observed.
Part 2.
An interesting finding reported by Paquette [7], was that whilst the atropisomer with the downwards facing carbonyl was usually the the thermodynamic product, this was not always the case. It was noted that the atropselectivity of the reaction was particularly sensitive to substitution at the *-carbon. For instance, in methylated derviatives, substitution with a protected OH group, such as OMOM or OTBS, favours the carbonyl pointing downwards for R, and upwards for S.
To examine this interesting result, methylated models of 9 and 10 (9" and 10") were constructed in ChemBio3D with an OMe group substituted in the * position with R and S configurations. The were subjected to MM2 minimisation, the results of which are summerised in table 6.
| Energies (kcal/mol) | ||||
|---|---|---|---|---|
| 9''R | 10''R | 9''S | 10''S | |
| Stretch | 4.6146 | 4.7903 | 4.5607 | 4.821 |
| Bend | 20.2844 | 18.6454 | 19.7901 | 20.0545 |
| Stretch-Bend | 0.8961 | 0.9116 | 0.8728 | 0.9877 |
| Torsion | 22.131 | 22.4621 | 21.3192 | 23.116 |
| Non-1,4 VDW | 0.3158 | 0.5344 | 0.4282 | -0.7809 |
| 1,4 VDW | 17.4661 | 17.5659 | 17.0709 | 18.0639 |
| Dipole/Dipole | -1.7532 | -2.554 | -1.7091 | -0.2735 |
| Total Energy | 63.9548 | 62.3558 | 62.3328 | 65.9886 |
The MM2 minimisation shows that whilst 10"R, with the carbonyl facing down, is the thermodynamic atropisomer for R-substitution; 9"S, with the carbonyl facing up, is the thermodynamic atropisomer for S- substitution. This is consistent with the experimental results reported by Paquette [7]. Visualisation of the structures in Jmol (click links in table) shows that, once again, this is to do with the conformation of the cyclohexane ring. For 9"R, the OMe is in an axial position, resulting in a 1,3-diaxial clash with the methyl group. On the other hand, 10"R has the opposite chair conformation so the OMe is positioned equatorially, avoiding such unfavourable interactions. Similarly, 10"S positions the OMe in an axial position; whereas 9"S, with the carbonyl pointing upwards, places the OMe in an equatorial position. This is why 9"S is the thermodynamically favoured atropisomer for S- substitution.
Modeling using semi-empirical molecular orbital theory
Regioselective Addition of Dichlorocarbene
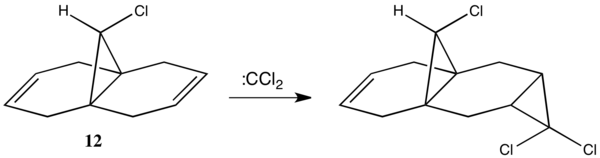
It was reported by Halton and Russell[1], that only one mono-adduct was isolated from the electrophilic addition of dichlorocarbene to molecule 12, as shown in Scheme. 5. The carbene adds exclusively to the double bond endo to the chlorine, attacking from the sterically-unhindered opposite face of the molecule.
Semi-empirical molecular orbital theory and density functional theory can offer insights as to whether it is electronic effects that are influencing the regioselectivity of the addition. Appropriate semi-empirical models such as PM6 or RM1 can be implemented through MOPAC, and DFT calculations through Gaussian 09.
Part 1.
A model of molecule 12 was constructed using ChemBio3D Ultra. The geometry was optimised using the MM2 force field to a maximum RMS gradient of 0.001 (click to view results and Jmol).
From the MM2 optimized geometry, an energy minimisation was performed and the molecular surfaces calculated using the MOPAC/PM6 semi-empirical method. When the molecular orbitals were visualised, it was noticed that whilst most of the lobes were symmetric, there were elements of asymmetry about the σ-plane. It was initially assumed that this was due to asymmetry in the MM2 optimised geometry. In MOPAC, the symmetry of the molecule can be constrained by adding the keyword AUTOSYM[2]. By specifying this keyword, symmetry in the starting material is automatically detected using the following rules:
- All bond-lengths which are within 0.0001Å are set equal.
- All bond-angles which are within 0.0057° are set equal.
- All dihedral angles which are within 0.0057° are set equal.
- All dihedral angles which are within 0.0057° of the negative of an existing dihedral are set equal to the negative of the existing dihedral.
The point point group is detected and is displayed in the output file at the start and end of the calculation[3]. Therefore, the MOPAC/PM6 calculation was repeated using the AUTOSYM keyword. As you can see from the output file the point group was correctly identified as Cs. However, the orbitals were still asymmetric about the molecule's plane of symmetry. It was concluded that this must be a bug in the calculation and a different method must be chosen. The view shown of the HOMO, looking down the σ-plane, is a good example of the asymmetry generated by MOPAC/PM6 through ChemBio3D.
From the original MM2 optimised geometry, an energy minimisation was performed and the molecular surfaces calculated using the MOPAC/RM1 method with the AUTOSYM keyword (view output). The point group was again correctly identified as Cs and inspection of the molecular orbitals revealed symmetry about the σ-plane. The same calculation was then repeated using the additional keyword GRAPHF[4], generating a MOPAC graphics file, allowing the orbitals to be visulaised in Jmol.
Ring Distortion: |
Inspection of the molecular orbitals reveal that the electron density of the HOMO is located on the endo alkene π bond. One would expect this to be the most reactive orbital towards electrophilic attack, which is consistent with the regioselectivity of the addition of dichlorocarbene. Electron density of the HOMO-1 is located on the exo alkene, which is 0.5884eV lower in energy. This means there would be a greater ΔE for any incoming electrophile for the HOMO-1 than that of the HOMO. The additional stability of the exo π bond can be rationalised by examining the favourable orbital alignment between the HOMO-1 and the LUMO, which corresponds to the σ* of the C-Cl bond. Donation of electron density from the exo π into the σ* may account for the stabilisation and reduced electron density on the exo alkene. This interaction manifests itself in a slight distortion of the exo ring upwards, towards the σ*. As you can see in the model above, the distance between the alkene carbons to the bridging cyclopropane carbon is 0.017nm shorter for the exo alkene than the endo. There also appears to be an unfavourable interaction in the HOMO between the endo π bond and a chlorine p-orbital, which may be raising the energy relative to the exo alkene.
Part 2.
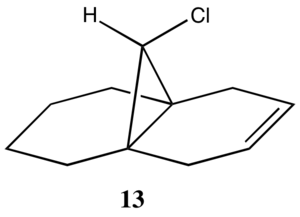
The .mol file from the MM2 optimised geometry of 12 was opened in Gaussview 5. A gaussian input file was set up to perform an energy minimisation and frequency calculation using the B3LYP hybrid-DFT functional and the 6-31G(d,p) basis set, with the point group symmetry contrained to Cs. The structure was then edited to give the exo-hydrogenated structure 13, in order to examine what effect the presence of the exo- double bond has on the C-Cl stretching frequency. Again, a gaussian input file was set up to perform the same calculation (B3LYP/6-31G(d,p) opt freq), although this time without constraining to a point group. Both files were run on Gaussian 09 through the SCAN cluster.
The .log output files were saved and molecular vibrations visualised on Gaussview 5. The results are summerised in Table 7 (click links for GIF animation).
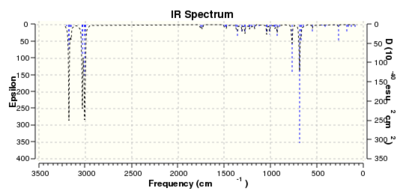
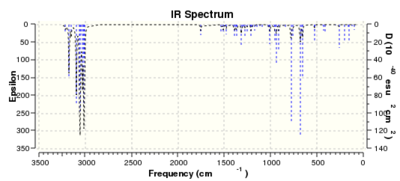
| Frequency (cm-1) | ||
|---|---|---|
| 12 [5] | 13 [6] | |
| C-Cl | 770.89 | 780.00 |
| C=C exo | 1737.07 | - |
| C=C endo | 1757.35 | 1753.76 |
The vibrational mode corresponding to the C-Cl stretch was found to increase in wavenumber for molecule 13, with the exo-double bond replaced by a single bond. This indicates a stronger C-Cl bond for 13 than for 12. This is consistant with the semi-empiracal orbital analysis, whereby donation from the π-bond of the exo alkene into the σ* C-Cl would decrease the strength of the C-Cl bond and result in a weaker stretching frequency. Absence of this interaction would result in less anti bonding character, a stronger C-Cl bond and, hence, a stronger stretching frequency as is observed.
The C=C stretches have also been identified. The C=C stretch for the endo bond is higher in wavenumber than that of the exo bond in molecule 12. This is consistent with the endo bond having greater electron density than that of the exo, making it more amenable to electrophilic attack. The exo bond's stretching frequency is much lower that of the endo bond in either 12 or 13, further supporting the notion of π-donation into the σ*. Interestingly, the stretching frequency of the endo bond in 12 is higher than that of 13. From this, one might predict that 12 would be slightly more reactive towards electrophiles that its hydrogenated derivative, 13.
Ring Distortion: |
Out of curiosity, the molecular orbitals generated by B3LYP/6-31G(d,p) were visualised for comparison with the orbitals generated by MOPAC/RM1. This was to see how well the semi-empirical method matches up to the higher level, DFT method. As the cube files generated by Gaussian are large in size, they were converted to the .jvxl format using the desktop Jmol app. The main difference between the two sets of orbitals is that the ordering is slightly different. Whilst the HOMO-1 and HOMO remain the same, the C-Cl σ* orbital is now the LUMO+2, rather than the LUMO. As the orbitals are generated through a higher level of theory, it is most likely that the B3LYP/6-31G(d,p) ordering is correct. This ordering is also consistent with that reported in the literature [7]. The distortion of the exo-ring is still observed in the DFT-optimised geometry , with the exo-alkene carbons 25nm closer than the endo-alkene carbons to the bridging cyclopropane carbon.
Part 3.
To explore the effect of the exo-double bond on the C-Cl stretching frequency further, several molecules were prepared with various electron donating and electron withdrawing substituents on the exo-alkene. One would assume, based on the analysis above, that electron donating substituents would increase electron density on the alkene resulting in a decrease in Cl-C stretching frequency in comparison to 12. Similarly, one would expect electron withdrawing substituents to decrease electron density on the alkene resulting in an increase in stretching frequency in comparison to 12.
The results of the frequency calculation are summerised in the table 8.
| substituent | νC=C (endo)(cm-1) | νC=C (exo)(cm-1) | νC-Cl(cm-1) |
|---|---|---|---|
| (12) H [5] | 1757.35 | 1737.07 | 770.89 |
| (14) OMe [8] | 1755.78 | 1762.39 | 775.70 |
| (15) CN [9] | 1757.13 | 1670.36 | 772.62 |
| (16) Me [10] | 1755.59 | 1747.08 | 768.16 |
Ranking by exo-alkene stretching frequency gives a good indication of the electron density on the exo-alkene. The electron withdrawing substituent, CN (15), gives a lower exo-alkene stretch of 1670 cm-1 compared to 12. Whereas, the moderately electron donating Me (16) gives a higher stretching frequency of 1747 cm-1 and the strongly electron donating OMe (14) gives and even higher stretch of 1762 cm-1. This order is as one would expect for the selected substituents. The effect of this electron density on the C-Cl stretch follows the rationale outlined above, for 15 and 16. The reduced electron density on the exo-alkene of 15 results in an increase in the C-Cl stretching frequency in comparison to 12. Similarly, the increased electron density on the exo-alkene of 16 results in a decrease in the C-Cl stretching frequency in comparison to 12. However, 14 does not appear to fit this trend. The OMe substituent clearly imparts the most electron density to the exo-alkene. So much so, that the stretching frequency is higher that that of the endo-alkene. Examination of the molecular orbitals reveals that for 14, the exo-alkene π-bond is now the highest occupied molecular orbital. Yet, the stretching frequency for C-Cl is higher than that of 12 and even that of 15. This is a surprising result as is does not appear to fit with the previous analysis where greater electron density leads to greater donation into C-Cl σ*, an increase in C-Cl antibonding character and a reduction in the C-Cl stretching frequency.
One observation is that, in 12, both the HOMO and HOMO-1 are significantly delocalised across the C-Cl bond. This arises from orbital mixing with the HOMO-3, which appears to correspond to a π*-type orbital across the C-Cl bond. In 14, significant orbital mixing with HOMO-3 is only observed with the HOMO-1, now corresponding to the endo-π bond. It appears that the increased electron density from the OMe substituents in 14 has raised the energy of the exo-π bond to such an extent that orbital mixing with the HOMO-3 is greatly reduced. If this outways any increase in donation to the C-Cl σ*, then the net effect will be a reduction in antibonding character across the C-Cl bond and an increase in the stretching frequency, as is observed. In fact, it may be that donation into the C-Cl σ* from the exo-π is a minor effect when it comes to the stabilisation of the HOMO-1 compared to the HOMO in 12, especially considering the large ΔE between the participating orbitals. It may be better explained by a greater extent of orbital mixing between the exo-π and the HOMO-3.
| 12 | 14 | ||||
|---|---|---|---|---|---|
|
|
- ↑ http://dx.doi.org/10.1021/jo00019a015
- ↑ http://openmopac.net/manual/autosym.html
- ↑ http://openmopac.net/manual/point_group_theory.html
- ↑ http://openmopac.net/manual/graph.html
- ↑ 5.0 5.1 DOI:10042/to-12853
- ↑ DOI:10042/to-12854
- ↑ http://dx.doi.org/10.1039/P29920000447
- ↑ DOI:10042/to-12853
- ↑ DOI:10042/to-12853
- ↑ DOI:10042/to-12853
Monosaccharide chemistry: glycosidation
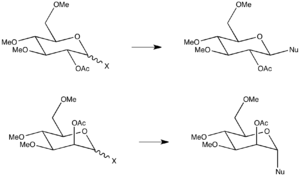
In glycosidation reactions, leaving group X is substituted by an incoming nucleophile. Neighbouring group participation from the O-acetyl group, in position 2 of the pyranose ring, directs the face of attack, resulting in a 1,2-trans relationship in the product. Hence, stereoselectivity for either the α- or β-anomer is seen to depend on the stereochemistry of O-acetyl group (Scheme 7). However, these reactions often deliver less than 99% selectivity for the 1,2-trans product, which is a requirement to efficient solid phase synthesis [1]. This may be because certain conformations allow for neighbouring group participation to the other face of the ring, or that certain conformations do not allow for neighbouring group participation to occur and the directing effect is lost.
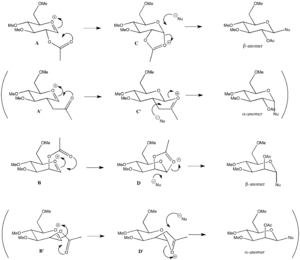
The aim is to examine the facial preference for incoming nucleophilic attack by modelling the oxonium cation with and without neighbouring group participation with MM2 and MOPAC/PM6. The conventional mode of participation will be examined (A, C, B and D) as well as a possible alternative mode of participation (A', C', B' and D') a illustrated in Scheme 8.
| energies (kcal/mol) | energy difference (kcal/mol) | energies (kcal/mol) | energy difference (kcal/mol) | |||
|---|---|---|---|---|---|---|
| A | A' | B | B' | |||
| Stretch | 2.6283 | 2.2373 | 0.3910 | 2.6405 | 2.4157 | 0.2248 |
| Bend | 12.7740 | 9.2852 | 3.4888 | 11.4460 | 11.1836 | 0.2624 |
| Stretch-Bend | 0.9398 | 0.7834 | 0.1564 | 0.8744 | 0.7869 | 0.0875 |
| Torsion | 1.7303 | 1.7000 | 0.0303 | 0.9854 | 0.9499 | 0.0355 |
| Non-1,4 VDW | 2.1704 | -2.7354 | 4.9058 | 1.4499 | -0.5396 | 1.9895 |
| 1,4 VDW | 19.5306 | 19.7049 | -0.1743 | 19.4758 | 19.9537 | -0.4779 |
| Charge/Dipole | -40.0090 | -8.1852 | -31.8238 | -34.4282 | -27.0912 | -7.337 |
| Dipole/Dipole | 7.9847 | 3.9058 | 4.0789 | 6.9932 | 6.5677 | 0.4255 |
| Total Energy | 7.7491 | 26.6960 | -18.9469 | 9.4370 | 14.2267 | -4.7897 |
| energies (kcal/mol) | energy difference (kcal/mol) | energies (kcal/mol) | energy difference (kcal/mol) | |||
|---|---|---|---|---|---|---|
| A | A' | B | B' | |||
| Heat of formation | -91.66313 | -85.75198 | -5.91115 | -88.53126 | -76.54449 | -11.98677 |
The results of minimisation of A, A', B, B' can be seen above in tables 9 and 10. The aim was to find two stable conformations for A and B where the O-acetyl group pointed above or below the plane of the oxonium cation. The structures found by MM2 minimisation were used as starting structures for MOPAC/PM6 minimisation. The most stable conformations, A and B, corresponded to positioning of the O-acetyl group towards the face that would lead to conventional neighbouring group participation and 1,2-trans products. A' and B', which corresponded to positioning of the O-acetyl group towards the alternative face, were found to be considerably higher in energy for both methods. So much so, that the population of these species in solution would be negligible (a difference of 3kcal/mol ≈ 99:1).
It must be said the flexibility in orientation of the methanol groups about the ring made finding the lowest energy conformations with MM2 very time consuming. This is because each orientation of the groups gave local minima, which had to individually screened. Great difficulty was often experienced in re-locating previously found minima with particularly low energies. Quite often this resulted in settling for higher energy conformations. This problem was not experienced with PM6, with MOPAC consistently optimising to the same low energy conformation. This is perhaps not surprising, considering that molecular mechanics is not well suited to chemical problems where charge delocalisation or other electronic effects are present. This is because the atom types, charges associated with atoms and their bond types are specified before the minimisation and are not subject to change, which can often give an unrealistic picture. In this respect, whilst MM2 may be useful for screening conformations to provide approximate geometries for further optimisation, the focus for chemical analysis should be on the results of the MOPAC/PM6 energy minimisation.
The positioning of the O-acetyl group in the MOPAC/PM6 optimised A and B, and lengthening of the O+=C bond, show that the structures have optimised to a geometry where the participating neighboring group, O-acetyl, is already participating, despite not being specified in the starting structure. This clearly shows that participation and delocalisation of the charge to the O-acetyl group is a spontaneous and favourable process for these conformations.
Interestingly, for A' where the O-acetyl group is not in an appropriate orientation to participate, the C-6 OMe oxygen has bent over to stabilise the charge. This may explain why the difference in energy is less than for B', where no neighbouring group participation is observed. This would mean that there would be no facial directing effects, although as previously mentioned, the energy is so much higher that one would expect a negligible population in solution.
The same molecules were then minimised with MM2 followed by MOPAC/PM6, this time with neighbouring group participation specified in the starting geometries. The results are summarised in tables 11 and 12.
| energies (kcal/mol) | energy difference (kcal/mol) | energies (kcal/mol) | energy difference (kcal/mol) | |||
|---|---|---|---|---|---|---|
| C | C' | D | D' | |||
| Stretch | 1.9288 | 2.9390 | -1.0102 | 1.8209 | 2.8121 | -0.9912 |
| Bend | 12.7809 | 19.6974 | -6.9165 | 18.1083 | 17.8415 | 0.2668 |
| Stretch-Bend | 0.6520 | 0.8005 | -0.1485 | 0.7141 | 0.7922 | -0.0781 |
| Torsion | 7.8528 | 7.1132 | 0.7396 | 7.9961 | 7.2672 | 0.7289 |
| Non-1,4 VDW | -2.6503 | -3.6699 | 1.0196 | -3.4525 | -2.5673 | -0.8852 |
| 1,4 VDW | 18.0099 | 19.0698 | -1.0599 | 17.8207 | 19.2775 | -1.4568 |
| Charge/Dipole | -10.5383 | 2.0865 | -12.6248 | -7.4090 | -2.7178 | -4.6912 |
| Dipole/Dipole | -1.1068 | 0.0239 | -1.1307 | -1.5858 | 0.1099 | -1.6957 |
| Total Energy | 26.9291 | 48.0603 | -21.1312 | 34.0127 | 42.8154 | -8.8027 |
| energies (kcal/mol) | energy difference (kcal/mol) | energies (kcal/mol) | energy difference (kcal/mol) | |||
|---|---|---|---|---|---|---|
| C | C' | D | D' | |||
| Heat of formation | -91.65991 | -65.49634 | -26.1636 | -88.53397 | -66.67342 | -21.8606 |
The heat formations for C and D are practically identical to the heat of formations for A and B, which confirms that A and B had minimised to geometries where the O-acetyl group was participating in charge delocalisation. C' and D' are both considerably higher in energy that C' and D', where neighboring group participation was not specified in the starting material. This indicates that for these conformations, neighbouring group participation to the alternative face of the oxonium cation is not favourable.
In conclusion, these calculations show that neighboring group participation is a favourable and spontaneous process and results in the lowest energy conformations for each monosaccharide. Conformations where neighboring group participation does not occur are higher in energy and would have low populations in solution. Neighboring group participation to the alternative face of the oxonium cation is not favourable. These findings explain why there is a high preference for 1,2-trans products in glycosidation reactions where neighboring group participation can occur. However, further calculations are needed to provide a satisfactory answer as to why selectivity for 1,2-trans products are usually less that 99%.
Structure based Mini project using DFT-based Molecular orbital methods
The structure and conformers of Stagonolide D
Introduction
Cirsium arvense, otherwise known as the creeping thistle or the Canada thistle, is a perennial weed. As an invasive species, it competes with crops and, as such, has become a problem in North America and Europe [1]. In 2007, the isolation and characterisation of Stagonolide A was reported [2]. This small molecule was a pytotoxic metabolite isolated from a liquid culture of Stagonospora cirsii, a fungal pathogen of Cirsium arvense. It was shown to inhibit root growth, and was identified as a possible candidate for a biological herbicide[3] to control the weed. In 2008, the isolation and characterisation of nine more metabolites, Stagonolide B-F [4]and Stagonolide G-I and Modiolite A [5], were reported from solid cultures of Stagonospora cirsii.
A recently published total synthesis of Stagonolide D by Ramana et al [6], found that the 1H-NMR and 13C-NMR of the structure, as proposed by the original characterisation (1), did not match up to the 1H-NMR and 13C-NMR of the isolated natural product. They went on to synthesise an alternative isomer (2'), of which the NMR data did match with that of the isolated natural product. This new structure was found to have an optical rotation of opposite sign to that of natural stagonolide D. Therefore, they proposed an appropriate structural revision (2). Interestingly, the NMR spectra of both the synthesised proposed structure and revised structure showed two sets of peaks with slightly different chemical shifts. These were attributed to two slowly equilibrating, major and minor conformers. It was only the major conformer of the revised structure that matched the NMR data of the isolated natural product. If they are correct, it suggests that the final step of the synthesis, the ring closing metathesis, generated two antropisomers of the molecule.
However, another total synthesis of Stagonolide D was publish shortly before this paper, by Nanda et al [7]. They too synthesised the originally proposed structure, yet the 1H-NMR and 13C-NMR data they report in the paper matches well with the isolated natural product, confirming the original structure. Curiously, the attached 1H-NMR spectra in the supplementary information does not match the peak data given in the experimental section of the paper. This spectra, labeled as that of Stagonolide D, does not match that of the isolated natural product or the revised structure reported by Ramana. The final step in the Nanda synthesis was also a ring closing metathesis, although no evidence of antropisomerism was observed in the NMR.
This project aims to investigate the uncertainties surrounding the structure of Stagonolide D. Firstly, the low energy conformation(s) of the originally proposed structure (1) and the alternative synthetic isomer (2') will be identified, using semi-empirical moleular orbital theory and DFT geometry minimisations. Once the low energy conformer(s) are found, prediction of the 1H-NMR and 13C-NMR spectra should allow for identification of the major and minor antropisomers observed by Ramana. These calculation should also resolve the contradiction between the confirmation of the originally proposed structure by Nanda, and the rejection of the originally proposed structure by Ramana.
Location of low energy conformers
Models of 1 (given the label O) and 2' (given the label I) were constructed using chembio3D, as well as a plastic physical model to aid visualisation. Eight conformers were found for both 1 and 2' by inspection, the geometries of which were minimised by MOPAC/PM6. These were categorized into four main-conformers (labeled 1 - 4) resulting from the relative orientation of the double bond and ester bond, each with two chair-like or twist-boat-like sub-conformers (labeled a and b) resulting from carbon-3 pointing up or down.
The structures of each of these conformations can be seen in table 13.
| O1a | O1b | O2a | O2b | O3a | O3b | O4a | O4b | |
|---|---|---|---|---|---|---|---|---|
| ΔH (kcal/mol) |
-141.37423 | -139.87433 | -138.76809 | -139.53815 | -138.06490 | -140.03708 | -140.84378 | -139.19046 |
| I1a | I1b | I2a | I2b | I3a | I3b | I4a | I4b | |
| ΔH (kcal/mol) |
-142.32658 | -140.70779 | -140.03046 | -137.51099 | -136.78381 | -139.34324 | -138.02835 | -139.56015 |
Calculation of 13C-NMR
A gaussian input file was prepared, based on the MOPAC/PM6 optimised geometries of each of the above conformations, to perform a DFT optimisation, as specified by:
- # opt mpw1pw91/6-31G(d,p) scrf=(cpcm,solvent=chloroform)
A gaussian input file was then prepared from the formatted checkpoint file of each of the DFT optimised geometries to perform a GAIO NMR calculation as specified by:
- # nmr=giao mpw1pw91/6-31g(d,p) scrf=(cpcm,solvent=chloroform)
This method was chosen as it has been shown to predict 13C-NMR shifts to an acceptable accuracy whilst using the modest and inexpensive 6-31G(d,p) basis set [8]. A solvation model was chosen to minimise potential errors in the optimised geometries, relative energies and calculated chemical shifts in comparison to the experimental data, measured in CDCl3. Both sets of calculations were implemented using Gaussian 09 on the SCAN cluster. The PM6 geometries were further optimised using density functional theory prior to the NMR calculation, as accurate relative energies are crucial for calculating NMR data in molecules with several low energy conformations. This is because each conformation that interconverts faster than the NMR timescale will have an effect on the experimentally observed chemical shifts if it has a significant population. Therefore, using the calculated energies for each conformation relative to the lowest energy conformation of each molecule, the Boltzmann populations in solution were obtained [9].
This data is summarised in Table 14.
| O1a [10] [11] | O1b [12] [13] | O2a [14] [15] | O2b [16] [17] | O3a [18] [19] | O3b [20] [21] | O4a [22] [23] | O4b [24] [25] | |
|---|---|---|---|---|---|---|---|---|
| Total energy (Hartrees) | -690.19707265 | -690.19304602 | -690.18205613 | -690.18531163 | -690.18772229 | -690.19218504 | -690.19511334 | -690.19736046 |
| Relative energy (kcal/mol) | 0.1806035 | 2.707351953 | 9.603611992 | 7.560754915 | 6.048042939 | 3.247625056 | 1.410089078 | 0 |
| Boltzmann population | 0.399731 | 0.005619 | 4.95056E-08 | 1.55625E-06 | 2E-05 | 0.002257 | 0.050182 | 0.542189 |
| NMR peak data | link | link | link | link | link | link | link | link |
| I1a [26] [27] | I1b [28] [29] | I2a [30] [31] | I2b [32] [33] | I3a [34] [35] | I3b [36] [37] | I4a [38] [39] | I4b [40] [41] | |
| Total energy (Hartrees) | -690.198975 | -690.1953307 | -690.1817656 | -690.1847384 | -690.1868985 | -690.1918577 | -690.1970615 | -690.1941203 |
| Relative energy (kcal/mol) | 0 | 2.286801382 | 10.79908028 | 8.933576206 | 7.578093002 | 4.466141768 | 1.200707993 | 3.046376494 |
| Boltzmann population | 0.86263 | 0.01818 | 1.04723E-08 | 2.44044E-07 | 2.4E-06 | 0.000459 | 0.113684 | 0.005044 |
| NMR peak data | link | link | link | link | link | link | link | link |
As you can see, there are two conformations for both 1 and 2' with significant populations in solution (bold). In both molecules, these correspond to conformations where the ester carbonyl is pointing up. Conformations where the ester carbonyl is pointing down (O2-O3, I2-I3) are markedly higher in energy and have very low, in some cases insignificant, populations. The two pairs of low energy conformations differ in the orientation of the double bond. If rotation of the E-alkene occurs faster than the NMR timescale, then both of the pairs would contribute towards the observed NMR shifts. However, if rotation of the alkene is restricted so that it occurs slower that the NMR timescale, then two sets of peaks would be observed.
| carbon number | natural stagonolide D | O1-4 | I1-4 | ||
|---|---|---|---|---|---|
| shift (ppm) | shift (ppm) | difference | shift (ppm) | difference | |
| 1 (3) | 173.5 | 167.90 | 5.60 | 169.10 | 4.40 |
| 5 (5) | 134.2 | 134.90 | -0.70 | 133.97 | 0.23 |
| 6 (10) | 128.1 | 121.14 | 6.96 | 126.13 | 1.97 |
| 4 (6) | 75.1 | 71.28 | 3.82 | 74.15 | 0.95 |
| 9 (7) | 65.7 | 66.73 | -1.03 | 66.34 | -0.64 |
| 8 (8) | 58.2 | 57.35 | 0.85 | 58.26 | -0.06 |
| 7 (9) | 55.4 | 56.18 | -0.78 | 55.83 | -0.43 |
| 3 (1) | 35 | 35.34 | -0.34 | 37.43 | -2.43 |
| 2 (2) | 31.2 | 31.50 | -0.30 | 32.53 | -1.33 |
| 10 (13) | 16.2 | 18.38 | -2.18 | 17.86 | -1.66 |
The Boltzmann weighted 13C-NMR shifts for both molecules 1 and 2' were calculated and compared to the experimentally observed shifts for the natural Stagonolide D. The deviations in ppm for each carbon are shown in table 15 (Gaussian atom numbers in brackets) and the corresponding chart. An error of about 5ppm was observed for carbon 1 in both molecules. A systematic error for ester carbonyl carbons of 4-5 ppm for mpw1pw91/6-31g(d,p) GAIO calculations has been reported in the literature; indeed, a suitable correction brings these calculated shifts in line with that of the natural product. The largest deviation in chemical shift is around 7 ppm for carbon 6 of O1-4, compared to just 2 ppm for I1-4. Interestingly, this corresponds to the alkene carbon nearest to the epoxide ring. For O4b, the highest populated conformation of O1-4, the alkene is oriented in the opposite direction to that of I1a, the highest populated conformation of I1-4. This may suggest that in the natural product the alkene is oriented as in I1a. The second largest deviation, apart from carbon-1, is for carbon-4, which corresponds to that of the secondary alcohol who's stereochemistry is in dispute. As before, I1-4 has a much lower deviation that O1-4, which may suggest that the natural product does indeed have the structure of 2 as reassigned by Ramana.
The calculated shifts were then grouped into two for each molecule, entertaining the possibility of atropisomers separated by the orientation of the double bond. The relative energies and Boltzmann populations were re-calculated for each individual atropisomer (O1-O2, O3-O4, I1-I2, I3-I4), the results of which are summerised in table 16..
| O1a | O1b | O2a | O2b | |
|---|---|---|---|---|
| Total energy (Hartrees) | -690.19707265 | -690.19304602 | -690.18205613 | -690.18531163 |
| Relative energy (kcal/mol) | 0 | 2.526748453 | 9.423008491 | 7.380151415 |
| Boltzmann population | 0.986134 | 0.013862 | 1.2213E-07 | 3.83926E-06 |
| O3a | O3b | O4a | O4b | |
| Total energy (Hartrees) | -690.18772229 | -690.19218504 | -690.19511334 | -690.19736046 |
| Relative energy (kcal/mol) | 6.048042939 | 3.247625056 | 1.410089078 | 0 |
| Boltzmann population | 3.36236E-05 | 0.003796 | 0.084389 | 0.911781 |
| I1a | I1b | I2a | I2b | |
| Total energy (Hartrees) | -690.198975 | -690.1953307 | -690.1817656 | -690.1847384 |
| Relative energy (kcal/mol) | 0 | 2.286801382 | 10.79908028 | 8.933576206 |
| Boltzmann population | 0.97936 | 0.02064 | 1.18894E-08 | 2.77067E-07 |
| I3a | I3b | I4a | I4b | |
| Total energy (Hartrees) | -690.1868985 | -690.1918577 | -690.1970615 | -690.1941203 |
| Relative energy (kcal/mol) | 6.377385009 | 3.265433775 | 0 | 1.845668501 |
| Boltzmann population | 2.01745E-05 | 0.003854 | 0.953803 | 0.042323 |
| carbon number | natural stagonolide D | O1-2 | O3-4 | I1-2 | I3-4 | ||||
|---|---|---|---|---|---|---|---|---|---|
| shift (ppm) | shift (ppm) | difference | shift (ppm) | difference | shift (ppm) | difference | shift (ppm) | difference | |
| 1 (3) | 173.5 | 168.74 | 4.76 | 167.34 | 6.16 | 169.22 | 4.28 | 168.20 | 5.30 |
| 5 (5) | 134.2 | 134.33 | -0.13 | 135.29 | -1.09 | 133.83 | 0.37 | 134.95 | -0.75 |
| 6 (10) | 128.1 | 123.77 | 4.33 | 119.35 | 8.75 | 127.40 | 0.70 | 116.73 | 11.37 |
| 4 (6) | 75.1 | 69.35 | 5.75 | 72.59 | 2.51 | 74.75 | 0.35 | 69.71 | 5.39 |
| 9 (7) | 65.7 | 66.39 | -0.69 | 66.95 | -1.25 | 66.23 | -0.53 | 67.10 | -1.40 |
| 8 (8) | 58.2 | 56.50 | 1.70 | 57.94 | 0.26 | 58.37 | -0.17 | 57.47 | 0.73 |
| 7 (9) | 55.4 | 56.11 | -0.71 | 56.23 | -0.83 | 55.76 | -0.36 | 56.35 | -0.95 |
| 3 (1) | 35 | 35.65 | -0.65 | 35.12 | -0.12 | 38.26 | -3.26 | 31.32 | 3.68 |
| 2 (2) | 31.2 | 28.74 | 2.46 | 33.38 | -2.18 | 32.76 | -1.56 | 30.81 | 0.39 |
| 10 (13) | 16.2 | 17.57 | -1.37 | 18.93 | -2.73 | 17.58 | -1.38 | 19.87 | -3.67 |
Out of the four calculated atopisomers, I1-2 stands out as matching the experimental NMR data of stagonolide D markedly better than the others. The error in ppm for carbon 5, 6, 4, 9, 8 and 7 is less that 1ppm, with a maximum deviation of 3ppm corresponding to carbon 3. The fit to the experimental data is better than for I1-4, and each of the other atropisomers have much larger maximum deviations, especially at key carbons such as 6 and 4.
Examination of the molecular orbitals of the various conformations reveals that there is significant transannular overlap between that HOMO, which corresponds to the π-orbital of the alkene, and the unoccupied π* of the ester carbonyl; particularly with the lobe positioned over the carbonyl carbon (carbon 1). It is difficult to compare the extent of overlap between conformations, but frequency analysis and examination of the C=O stretch would be a good method of quantifying the interaction. This transannular interaction may be one of the key factors that restricts rotation of the alkene bond as a poor alignment of the π-faces would cause reduction in orbital overlap. It would be interesting to see whether how the frequency of the C=O stretch changes for the higher energy conformations such as I2a, where the ester carbonyl group is pointing downwards.
Assignment of atropisomers
An interesting observation made by Ramana in the synthesis of 1 and 2', was that the NMR spectra for both compounds showed two sets of peaks, assigned as slowly equilibrating major and minor conformers [6]. For 2', only the chemical shifts of the major conformer matched that of the natural product. This may suggest that the final ring closing metathesis generated two sets of atropisomers or, as suggested by Ramana, that there exists two conformations which interconvert slower than the NMR timescale.
The calculated chemical shifts for O1-2, O3-4, I1-2 and I3-4 were compared to the reported chemical shifts of the major and minor conformations for 1 and 2', as synthesised by Ramana. The average deviation (excluding carbon-1) was used to quantify the fit and the results are summarised in table 18.
| 1 major | 1 minor | 2' major | 2' minor | |
|---|---|---|---|---|
| O1-2 | 1.21 | 1.70 | 2.00 | 1.67 |
| O3-4 | 2.83 | 0.94 | 2.21 | 2.08 |
| I1-2 | 2.40 | 2.01 | 0.97 | 3.42 |
| I3-4 | 2.60 | 1.45 | 3.17 | 1.17 |
| File:Omajor njm08.pdf | File:Ominor njm08.pdf |
| File:Imajor njm08.pdf | File:Iminor njm08.pdf |
For each set of major and minor peaks, one set of calculated chemical shifts matched noticeably better than the others, especially for 1 minor and 2' major. This suggests that the two sets of peaks found in Ramana's spectra are indeed due to conformations of the same molecule. Interestingly, the relative peak heights observed by Ramana do not correspond to the Boltzmann populations as determined by the relative energies from the calculated structures. For example, the lowest energy conformation of 1 was calculated to be O4b. But O3-4, where O4b has a 91% population, matches the NMR of the minor conformer. This suggests that the conformations observed in the experimental spectra are not at thermodynamic equilibrium, which implies that they are true atropisomers, unable to intervonvert. Its feasible to see how these atropisomers could have come about from the final ring closing metathesis, especially as it appears they differ by the orientation of the double bond.
The other explanation is that the relative energies from the DFT optimised structure are inaccurate. This is quite likely since the modest 6-31G(d,p) basis set was used. The relative total energies were also approximated to be representative of the relative Gibbs free energies, which of course is not necessarily the case. By performing a frequency analysis, the entropy corrected energies can be obtained which would give more accurate populations.
The feasibility of repeating the optimisations and NMR calculations using methods that have been shown to give lower errors, was evaluated. The NMR for I1a was calculated from the mpw1pw91/6-31g(d,p) optimised structure using the following methods:
- # nmr=giao mpw1pw91/aug-cc-pvdz scrf=(cpcm,solvent=chloroform) [42]
- # nmr=giao b3lyp/aug-cc-pvdz scrf=(cpcm,solvent=chloroform) iop(3/76=1000001189,3/77=0961409999,3/78=0000109999) [43]
The first of these methods simply replaces the 6-31G(d,p) basis set with the aug-cc-pvdz basis set and has shown to reduce many of the systematic errors such as with the ester carbonyl carbon [8]. The second uses the WP04 functional, a version of the popular B3LYP functional that has been re-parametised specifically for calculating NMR shifts in chloroform [44]. Both methods took approximately 40 minutes of wall time on the SCAN, compared to ≈5 minutes with mpw1pw91/6-31g(d,p). Each of the 16 conformations would have to be re-optimised by the same method (ideally with frequency analysis) prior to NMR calculations, which took between 20-60 minutes of wall time for mpw1pw91/6-31g(d,p). Therefore, it was decided that these methods were too expensive given the limited time frame and requirement of the SCAN by other colleagues.
Even so, the errors were seen to be low enough to assign the structure of each of the atropisomers for 1 and 2' as represented by the lowest energy conformation. These structures can be seen below.
| 1 major (1) | 1 minor (1) | ||||
|---|---|---|---|---|---|
|
|
| ||||
| 2' major (2') | 2' minor (2') | ||||
|
|
|
Calculation of optical rotation
A Gaussian input file was prepared from the formatted checkpoint file of the DFT optimised structure of I1a to calculate its optical rotation, specified by:
- # cam-b3lyp/aug-cc-pvdz polar(optrot) scrf=(cpcm,solvent=chloroform) CPHF=RdFreq
The frequency was specified as 589nm in the input file to correspond to the sodium D lines. A similar input file was prepared for its enantiomer, I1a'.
The purpose of this calculation is to determine the sign of the optical rotation for I1a, which the calculations suggest is a representative structure for 2'; and the enantiomer I1a', which if correct would correspond to 2, or natural Stagonolide D. Ramana reported an [α]25D of +76.8 for 2', compared to a reported [α]25D of -82 for the natural product, leading to the reassignment of Stagonolide D as 2.
| I1a [45] | I1a' [46] | |
|---|---|---|
| [α]25D (calc.) | +114.97 | -114.86 |
| [α]25D (lit.) | +76.8 [6] | -82 [4] |
The optical rotation of I1a was found to be the same direction as that of 2', and the I1a' to be the same direction as natural stagonolide D. This supports the absolute sterochemistry of the reassigned structure of Stagonolide D (2).
Conclusions
The calculated 13C-NMR spectra and calculated optical rotation appear to support the reassignment of the structure of Stagonolide D by Ramana. The major and minor conformers found in the spectra of 1 and 2' were assigned to pairs of Boltzmann weighted conformers, differing in the orientation of the double bond. The relative peak heights observed in the experimental spectra do not reflect the populations of the conformers as calculated by Boltzmann statistics. This may suggest that the pairs are not at thermodynamic equilibrium and are atropisomers generated by the final synthetic step - the ring closing metathesis. This is also supported by the observation that only the major conformer of 2', I1-2, matches well with the NMR data of the natural product.
For a more definitive assignment, calculations should be repeated using higher levels of theory as described in previous sections. This is particularly true of the geometry optimisations to ensure accurate relative energies and representative populations.
It would be interesting to carry out further calculations to rationalise the relative stability and instability of the low and higher energy conformations. This would be done using molecular mechanics to evaluate the steric factors, and frequency analysis of the C=O stretch to assess the extent of the transannular interaction between the π- bond of the alkene and the π* of the ester carbonyl.
An issue not addressed was the confirmation of the originally proposed structure, 1, by Nanda [7]. There is definitely something odd about the paper. One point to note is that stagonolide D is one of the only isolated stagonolides that is a crystalline solid. Ramana's synthesis of 1 gave a yellow oil, whereas his synthesis of 2' gave a crystalline solid. The nature of the product synthesised by Nanda is not stated in the paper. The other point is that the 1H-NMR spectra attached in the supplementary information labeled as "stagonolide D" does not match the 1H-NMR peak data given in the experimental section of the paper. One of the reasons for repeating the NMR calculations at a higher level of theory such as WP04/aug-cc-pvdz, is that it has been shown to give acceptable predictions of 1H-NMR shifts [44], which may shed light on this problem.
The lack of any X-ray crystallography data may suggest a difficulty in obtaining high quality crystals, although this would allow for a definitive answer to the structure.
References and links
- ↑ http://www.wildflowers-and-weeds.com/weedsinfo/Cirsium_arvense.htm
- ↑ DOI:10.1021/jf070742c
- ↑ http://dx.doi.org/10.1016/S0261-2194(00)00092-2
- ↑ 4.0 4.1 DOI:10.1021/np0703038
- ↑ DOI:10.1021/np800415w
- ↑ 6.0 6.1 6.2 DOI:10.1021/jo202138g
- ↑ 7.0 7.1 http://dx.doi.org/10.1246/bcsj.20100197
- ↑ 8.0 8.1 DOI:10.1021/np0705918
- ↑ DOI:10.1021/cr200106v
- ↑ DOI:10042/to-12858
- ↑ DOI:10042/to-12874
- ↑ DOI:10042/to-12859
- ↑ DOI:10042/to-12875
- ↑ DOI:10042/to-12860
- ↑ DOI:10042/to-12876
- ↑ DOI:10042/to-12861
- ↑ DOI:10042/to-12877
- ↑ DOI:10042/to-12862
- ↑ DOI:10042/to-12878
- ↑ DOI:10042/to-12863
- ↑ DOI:10042/to-12879
- ↑ DOI:10042/to-12864
- ↑ DOI:10042/to-12880
- ↑ DOI:10042/to-12865
- ↑ DOI:10042/to-12881
- ↑ DOI:10042/to-12866
- ↑ DOI:10042/to-12882
- ↑ DOI:10042/to-12867
- ↑ DOI:10042/to-12889
- ↑ DOI:10042/to-12868
- ↑ DOI:10042/to-12883
- ↑ DOI:10042/to-12869
- ↑ DOI:10042/to-12884
- ↑ DOI:10042/to-12870
- ↑ DOI:10042/to-12885
- ↑ DOI:10042/to-12871
- ↑ DOI:10042/to-12886
- ↑ DOI:10042/to-12872
- ↑ DOI:10042/to-12887
- ↑ DOI:10042/to-12873
- ↑ DOI:10042/to-12888
- ↑ DOI:10042/to-128990
- ↑ DOI:10042/to-128991
- ↑ 44.0 44.1 DOI:10.1021/jo900482q
- ↑ DOI:10042/to-12892
- ↑ DOI:10042/to-12893