Rep:Mod:110101010110101010101011010111101010

The Cope Rearrangement

Introduction

Figure 1: The Cope Rearrangement of 1,5 - Hexadiene

Figure 2: Chair and Boat Transition Structures involved in Cope Rearrangement of 1,5 - Hexadiene

The subject of the first part of this investigation is the chemical reactivity problem posed by the Cope rearrangement of 1,5- hexadiene.

The Cope Rearrangement refers to the [3,3] - sigmatropic reaction of 1,5 - dienes developed by Arthur Cope. . The rearrangement involves 6 electrons as shown in Figure 1. Following the Woodward-Hoffman rules, the reaction is a thermally allowed 4n+2 electron process that proceeds via a Huckel topology .

The rearrangement has been widely studied (both experimentally and computationally) and today it is generally accepted that the rearrangment proceeds via a "chair" or "boat" transition structure (as shown in Figure 2) through a concerted mechanism .

There are three bonds between sp² carbon atoms in 1,5-hexadiene. These bonds are able to rotate freely and there exist three rotational minima around each of these three bonds. This gives rise to 27 possible conformations that 1,5-hexadiene is able to adopt. Due to symmetry and enantiomers, only 10 of these conformations are energetically different. The Newman projections of all these conformers can be found in Gung et al’s paper.

This report is concerned with locating low energy minima and transition structures on the C₆H₁₀ potential energy surface and investigating the preferred reaction mechanism.

Optimising the Reactants and Products

Method Used

In this part of the report, Gaussivew was used to prepare the required structures. Optimisations were performed using the Hartree-Fock level of theory using 3-21G basis sets and later using the Density Functional Theory (DFT) B3LYP level of theory using the 6-21G* basis set.

The Hartree Fock method approximates complex orbitals using a series of one electron orbitals. The core orbitals are described by 1 Slater Type Orbitals (STOs) and the valence orbitals are described by 2 STOs. The 3-21G basis set is an example of a split-valence basis set, where we sum 3 gaussian functions to describe the inner shell orbital, and use 2 gaussian functions to describe the first STO of the valence orbital and 1 gaussian function to describe the second STO. The 3-21G contracted basis set is relatively computationally untaxing, but at the expense of relatively low accuracy.

We also note that the HF level of theory uses the mean-field approximation (in simple terms, this involves approximating the effect of all other electrons with an electron through a "mean field"). Thus, electron correlation effects associated with electrons of opposite spins are ignored. (Even for electrons with the same spin, HF only accounts for a particular type of correlation, the exchange correlation. Interaction between electrons still follows the mean field approach. João (talk) 12:00, 20 March 2015 (UTC))

The DFT/B3LYP method used employs a higher level of theory. In this investigation, B3LYP is the hybrid functional used to approximate the exchange-correlation functional in the density functional theory (DFT) calculations. It combines a degree of the exact exchange from the HF theory with exchange and correlation terms obtained from the three parameters defined in Becke's original fitting of the analagous B3PW91 functional. . Hence, the B3LYP (DFT) method is better able to account for electron correlation effects. The 6-31G* basis set is similar to the 3-21G* basis set but instead it uses 6 Gaussian functions to describe the inner shell orbital, 3 Gaussian functions to describe the first STO of the valence orbital. Furthermore, the 6-21G* basis set takes polarisation in the 'p' orbitals into account (the shape of the orbital is distorted to account for a degree of 'd' orbital character. Overall thus, the DFT/B3LYP level of theory with the 6-21G* basis sets should yield more accurate results, at the expense of computational time. However, the DFT/B3LYP method is still known for its efficiency (is able to provide relatively very accurate results without too much an increase in computational time required).

After optimisation, the "Point Group" function under the "Edit" menu on Gaussview was used to probe the symmetry of the optimised structure. The point group symmetry assigned to the structures was the highest-order point group the structure could be approximated to under a "Default" (0.01) tolerance.

Lowest Energy Conformations

We begin by optimising two structures of 1,5 - hexadiene: one with an anti-periplanar conformation ("anti" linkage for the central four carbon atoms) and one with a gauche-linkage.

Hypothesis

Using an argument based on steric considerations, we might expect the optimised anti conformation to have a lower energy than the gauche conformation. This is the argument that in the gauche conformer, the two R groups will be closer in proximity to a level where the distance between the R groups (or specifically e.g. the H atoms on the R groups) may be smaller than the sum of their VDW radii. This would result in repulsive interactions which would lead to the gauche conformer being higher in energy than the anti-conformer. This argument successfully explains why the anti conformation of n-butane is the global minimum. Investigations have found that each gauche C-C-C-C unit in saturated hydrocarbons increases the energy of the conformation compared to the corresponding anti conformations by around 0.8 - 1.0 kJ/mol per C-C linkage. We may thus expect similar results for our computational study on the conformations of 1,5- hexadiene.

Results & Analysis

The table below shows the two optimised conformations of 1,5 - hexadiene. By comparing their structures and energies, the conformers are assigned as one of the low energy conformers in Appendix 1 on the instructions page for this course. The relative energy of the lowest energy conformer is taken as zero (in this case, the Gauche 3 conformer has been found to have lower energy than the Anti 4 conformer). The relative energy of the other conformation was determined by finding the energy difference between the conformers and the Gauche conformers and converting the value of relative energies from Hartrees to kcal/mol by using the conversion factor: 1 Hartree = 627.503 kcal/ mol.

Table 1: Optimised Gauche and Anti Conformations of 1,5 - Hexadiene

Conformer	Structure	Point Group Symmetry	Energy (Hartrees)	Relative Energy (kcal/mol)
Anti 4		C1	-231.69097055	1.06
Gauche 3		C1	-231.69266120	0.00

Analysis:

We find that in fact our calculations suggest that the optimised Gauche conformation has a lower energy than the Anti conformation. This is contrary to our expectations based on the conventional rules of alkane conformational analysis. A study by Gung et. al (using MP2/ 6-31G* level of theory) appears to reach the conclusion that the Gauche 3 conformation is in fact the global minimum for 1,5-hexadiene. Gung explains his results by suggesting an attractive interaction between the pi orbital of the C=C double bond and the nearby vinyl proton (C-H bond).

Figure 3: Annotated Diagram of HOMO of optimised Gauche 3 conformation

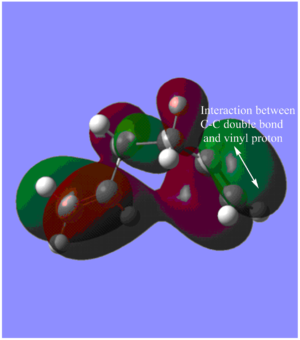
In fact, in the HOMO of our optimised structure (Figure 3), we do observe the aforementioned stabilising CH - pi interaction as highlighted through the annotations. Another stabilising interaction we note is due to the delocalisation as result of the in-phase overlap between the pi orbitals of the terminal double bonds resulting.

Below, we optimise all the 10 low energy conformations of 1,5-hexadiene. We may hypothesise that we too may find that the Gauche 3 conformation is the lowest energy conformation.

Table 2: Gauche and Anti Conformations of 1,5 - Hexadiene

Conformer	Structure	Point Group Symmetry	Energy (Hartrees)	Relative Energy (kcal/mol)
Gauche 1		C2	-231.68771617	3.10
Gauche 2		C2	-231.69166701	0.62
Gauche 3		C1	-231.69266120	0.00
Gauche 4		C2	-231.69153035	0.71
Gauche 5		C1	-231.68961576	1.91
Gauche 6		C1	-231.68916020	2.20
Anti 1		C2	-231.69260235	0.04
Anti 2		Ci	-231.69253528	0.08
Anti 3		C2h	-231.68907063	2.25
Anti 4		C1	-231.69097055	1.06

The results show that we find that the Gauche 3 conformation is in fact the lowest energy conformation. This is in agreement with Gung's results . However, another computational investigation by Rocque et al. finds the Anti 1 conformation to be lowest in energy.

It appears that there is a level of inconsistency in the energetic ordering of the conformations of 1,5-hexadiene between computational studies, and results may largely depend on the methods used. The Hartree-Fock method used in this report neglects the full effects of electron correlation. Thus various electronic effects, such as the CH-pi interaction discussed, are not fully considered. (Don't you show above that HF is capable of describing this effect? The general argument that the energy differences are small and thus sensitive to the method is however a good one. João (talk) 12:00, 20 March 2015 (UTC))

We note that the difference in energies of the optimised conformations are relatively small. We discussed above that the source of the relative instability of the gauche form of n-butane was due to steric repulsion (the distance between the H atoms on C1 and C4 in gauche n-butane is 2.35 Angstroms which results in repulsive interactions (Ref? João (talk) 12:00, 20 March 2015 (UTC))). However, for example in the Gauche 4 conformation, the distance between the H atoms on C2 and C5 is only 2.5 Angstroms. Therefore, unlike n-butane, we can understand why the energies of the gauche conformations are much more similar to the energies of the anti conformations for 1,5-hexadiene.

Conclusion

Overall, we understand that due to all the discussed subtle factors that the various conformations of 1,5-hexadiene are very close in energy. Perhaps, the most main conclusion we can draw from our investigation is that the 10 conformers are near-degenerate. Our findings show the Gauche 3 conformation is the lowest energy conformation, but we cannot conclude with much certainty that is the global minimum due to the very small energy differences between our optimized conformations, varying results in literature, and limitations associated with the method used. Rocque et al. has suggested that perhaps a CCSD(T) calculation with a significantly larger basis set may be used to determine which conformation is truly the global minimum.

Anti 2 Conformation

Optimising with HF vs DFT

Figure 4: A Gaussview image of Anti2 Conformer of 1,5 - Hexadiene showing atom labels

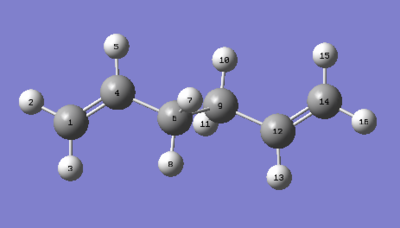
The structure of the Anti 2 conformation obtained after optimisation with HF/3-21G level of theory was reoptimised using B3LYP/6-21G* (DFT) level of theory. The bond lengths and dihedral angles can be probed in the final structures to analyse any difference in geometry. We summarise the results in the tables below. The atom labeling used to describe bonds in Table 3 are depicted in Figure 4.

Table 3: Structures of Anti 2 Conformation of 1,5- Hexadiene Obtained after Optimization with 3-21G (HF) and 6-21G* (DFT)

Level of theory used in Optimization	Structure	Point Group Symmetry	Energy (Hartrees)	Relative Energy (kcal/mol) (This is not meaningful, you can't compare absolute energies computed at different levels of theory. João (talk) 12:00, 20 March 2015 (UTC))
HF/3-21G		Ci	-231.69253528	1831.79
B3LYP/6-21G* (DFT)		Ci	-234.61171167	0.00

Table 4: Comparing Bond Length in Anti 2 Conformation Structures of 1,5- Hexadiene obtained after Optimization with 3-21G (HF) and 6-21G* (DFT)

Bond(s) Considered	Bond Lengths (Angstroms))
	HF/3-21G	B3LYP/6-21G*
C1-C4 & C12-C14	1.31608	1.33349
C4-C6 & C9-C12	1.50887	1.50424
C6-C9	1.55277	1.54811

Table 5: Comparing Dihedral Angles in Anti 2 Conformation Structures of 1,5- Hexadiene obtained after Optimization with 3-21G (HF) and 6-21G* (DFT)

Atoms	Dihedral Angle (Degrees)
	HF/3-21G	B3LYP/6-21G*
C1-C4-C6-C9	114.666	118.557
C4-C6-C9-C12	180.000	180.000
C6-C9-C12-C14	-114.666	-118.557

We observe that the geometry of the final structures obtained via optimisation using the different levels of theory are reasonably similar but there are slight noticeable differences. For example, we understand that the single bonds lengths are shorter, the double bond lengths are longer and select dihedral angles are larger in absolute value in the final structure obtained using the higher level of theory. Furthermore, we understand that even though there is only a slight change in geometry, there is a significant difference in the calculated energies of the optimised structures depending on the level of theory used. The relative energy of the final structure optimised using B3LYP/ 6-31G* level of theory compared to the structure optimised using HF/3-21G is 1831.79kcal/mol. This is around a 1000 orders of magnitude greater than the energy differences observed between the structures of the different conformation of 1,5-hexadiene optimised using HF/3-21G level of theory. (These energies are not comparable. What you can compare is how much do conformer energies differ at one level of theory and the other. João (talk) 12:00, 20 March 2015 (UTC))

This analysis highlights the variation in results one can obtain depending on which level of theory one uses for a calculation.

Frequency Analysis

A frequency calculations was performed on the optimised B3LYP/ 6-31G* Anti 2 Conformation structure using the B3LYP / 6-31G* level of theory.

Figure 5: IR Spectrum of Anti 2 Conformer of 1,5-Hexadiene obtained after optimization and frequency analysis using B3LYP/ 6-21G* (DFT) level of theory

Till now, we have optimised molecules to locate energy minima. When we run a frequency calculation, we are exploring the energy surface around the minimum to check it really is a minimum (second derivative is positive and energy rises in all directions) - therefore both calculations involve energy calculations. If we use a different method and basis set for the frequency, not only will the optimized molecule now have a different energy but the surrounding energy surface will be different too. Therefore, the frequency calculation will now be inconsistent with the optimisation calculation (our analysis in the previous section also helped us appreciate the variety in results one can obtain depending on the level of theory used for the calculation). The fact that the optimised molecule might not even be a minimum using the new method and basis set means that the frequency calculation is not valid (as the frequency calculation is only valid at stationary points). This is why the frequency calculation was conducted using the same level of theory as the optimisation and such consistency is maintained throughout this investigation.

One purpose of carrying out a frequency calculation is to check that the second derivative of the energy is positive and thus that the energy rises in all directions on the energy surface. The vibrational frequencies are computed by determining the second derivates of E with respect to qn and then transforming to mass-weighted coordinates. Therefore if all the frequencies computed are positive - this means that the energy rises in all directions on the energy curve when we deviate from our optimized molecule - and therefore we have found a minimum. If only one of the frequencies is negative (imaginary)- then the energy only falls in one direction (i.e. the reaction coordinate) and we have a transition structure. Thus, a frequency analysis was conducted to check that there were only real frequencies (no imaginary ones) to confirm that we had located an energy minimum.

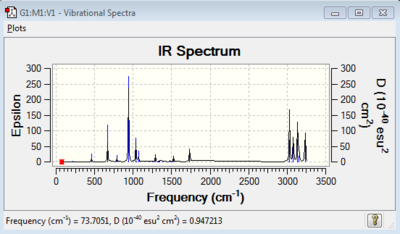
The second purpose to carrying out a frequency analysis is because it provides data regarding IR and Raman modes that we can use to compare with experimental results. The simulated IR spectrum obtained via the frequency calculation is shown in Figure 5. In the spectrum, we observe the expected 42 vibrational frequencies (3N-6 = 3(16) - 6 = 42).

Thermochemicical Analysis

Frequency calculations were performed on the optimised B3LYP/ 6-31G* Anti 2 Conformation structure at 298.15K (this is the default setting) and one at 0.00001K (using the additional keyword: temperature = 0.00001). The temperature of 0.00001K was used to investigate the frequency results near 0K as Gaussian does not recognize temperature = 0K (See "Problem Encountered" section).

The outputs of the calculations were used to locate thermochemical data under the "Thermochemistry" tab. The results are summarised below:

Table 6: Thermochemistry Energies: Results after Optimization and Frequency Analysis of Anti2 Conformer of 1,5 - Hexadiene with B3LYP/6-31G* level of theory

Values	T = 298.15 K	T = 0.00001 K
Sum of electronic and zero-point energies	-234.469214	-234.469214
Sum of electronic and thermal energies	-234.461866	-234.469214
Sum of electronic and thermal enthalpies	-234.460922	-234.469214
Sum of electronic and thermal Free energies	-234.500799	-234.469214

As expected, the sum of electronic and zero-point energies is less negative than the electronic energy (-234.61171167) as now the positive zero-point energy term is taken into account. The sum of electronic and zero-point energies is essentially the potential energy at 0K including the zero-point energy vibrational energy. Since both these constituent components (potential energy at 0K and zero-point vibrational energy) are temperature-independent, we can understand why this value is the same across the two temperatures.

The differences between the sum of electronic and zero-point energies and the other sums are all due to terms that are temperature-dependent. Therefore, we can understand why all these sums are equal at approximately 0K.

The sum of electronic and thermal energies include the contributions of translational, rotational, and vibrational energy modes and the sum of electronic and thermal enthalpies include the correction for RT (H = E + RT) (Under which conditions is this true? João (talk) 12:00, 20 March 2015 (UTC)). As these sums include terms that are increase in value with temperature (the contribution of the energy modes and RT respectively become more significant at higher temperature), we can understand why these values are less negative than preceding sums. The sum of electronic and thermal free energies further accounts for entropic contributions (G = H - TS) (Any idea how the entropy is calculated? João (talk) 12:00, 20 March 2015 (UTC)). As the entropic term is negative (-TS) and thus becomes more negative at higher temperatures, we understand why the sum of electronic and thermal free energy at T = 298.15K is more negative than the preceding sums at T = 298.15 K and even more negative than the corresponding term at approximately 0K.

Problem Encountered

Frequency Calculation on B3LYP/ 6-31G* optimised structure at T = 0K

When I tried to calculate the frequency analysis setting the temperature to 0K, the values of the energies through the analysis were:

Sum of electronic and zero-point Energies= -234.469214

Sum of electronic and thermal Energies= -234.461867

Sum of electronic and thermal Enthalpies= -234.460922

Sum of electronic and thermal Free Energies= -234.500799

I realized that there was an error because we expect the Sum of electronic and zero-point Energies to be equal at all temperatures and because we expect all four values to be equal at 0K.

Upon analysis of the output file, I realized that Gaussian had performed the calculation taking T = 298.15K (the default) because it does not recognize T = 0K as a valid temperature. This meant that the calculation performed was a similar calculation as the one performed without the additional keyword: "Temperature=0K".

The problem was solved by using a temperature of 0.00001K as a compromise.

Optimising Chair and Boat Transition Structure

In this next section, we endeavor to locate, analyse and compare the proposed "chair" and "boat" transition structures (shown previously in Figure 2) for the Cope rearrangement of 1,5-hexadiene. We attempt to find the chair transition structure using two methods: 1) by computing the force constant matrix (Hessian) at the beginning of the calculation (Direct Transition State Berny Method) and 2) using the redundant coordinate editor (frozen coordinate method). We also attempt to find the boat transition structure using two methods: 1) the QST2 method and 2) the QST3 method.

Optimising Chair Transition Structure

Method Used

An allyl fragment (CH₂CHCH₂) was optimised using 3-21G level of theory (3-21G is not a level of theory, is a basis set. João (talk) 12:00, 20 March 2015 (UTC)). Two of the optimised structures were used to create an input structure that resembles a chair structure (shown in Table 7 below). The distance between the fragments was adjusted to be approximately 2.2 Angstroms at each terminal end.

The guess chair structure was optimised to a transition structure using two methods.

Direct Transition state Berny Method (DTSBM): A optimisation and frequency (Opt + Freq) calculation (using 3-21G level of theory) was performed by using the option "Optimisation to a TS (Berny)", setting the force constants (Hessian) to be calculated Once, and using the additional keyword: "Opt = NoEigen". In this method, the calculation involves computing the Hessian in the first step which is updated as the optimisation proceeds.

Frozen Coordinate Method (FCM): The "Redundant Coordinate Editor" was used to freeze the distances between between both the terminal ends of the allyl fragments as they were in the input file (distances specified in Table 7). The rest of the structure was optimised to a minimum using HF/ 3-21G. The output was optimised to a transition structure (using Berny method) after the reaction coordinate was unfrozen. The "Calculate Force Constants" option was set as "Never".

For both cases, the vibrational frequencies computed as a result of the frequency calculations were analysed.

Once again, after optimisation, the "Point Group" function under the "Edit" menu on Gaussview was used to probe the symmetry of the optimised structure. The point group symmetry assigned to the structures was the highest-order point group the structure could be approximated to under a "Default" (0.01) tolerance.

Results & Analysis

Table 7 below shows the Chair Guess Transition structure used as an input in the two methods employed to locate the proposed chair transition structure.

Table 7: Chair Guess Transition Structure

Jmol Image	Atom Labeling	C1-C14 distance (Angstroms)	C6-C9 distance (Angstroms)
		2.19273	2.20871

Table 8 summarises the results of the two methods used to optimise to the chair transition state structure:

Table 8: Optimised Chair Transition Structures using Two Methods

Method Used	Jmol Image	Energy (Hartrees)	Point Group Symmetry	Imaginary Vibrational Frequency	Animation of Imaginary Vibration
Direct Optimization to a TS (Berny) Method (Hessian computed at beginning of calculation)		-231.61932215	C2h	-817.87
Frozen Coordinate Method		-231.61932229	C2h	-817.88

Analysis

We acquire the desired chair transition state structures using both methods:

1) Energies: The energies of both the structures are higher than the energies of all 10 low energy conformations of 1,5-hexadiene computed earlier. This is in line with our expectations since transition states correspond to maxima on the potential energy surface, and therefore we expect transition states to have relatively higher energies.

2) Point Groups: Our aim was to locate the chair transition structure which should have C_2h symmetry. This is exactly what we find in our optimised structures.

3) Frequency Analysis: For both structures, the frequency calculations gave one imaginary frequency. This means that at this point on the potential energy surface, the energy only falls in one direction (i.e. the reaction coordinate) and we have a transition structure. Furthermore, we can see that the animated vibration corresponds to the Cope rearrangement. This confirms that we have located a chair transition structure for the Cope rearrangement of 1,5-hexadiene. Furthermore, the motion observed in the animated vibration with the negative frequency supports the suggestion that bond breaking and bond formation is synchronous.

Comparison of two methods used

We understand that both methods used have been successful in locating the same desired chair transition state as illustrated by the near-identical energies of the two final structures.

The advantage of the method we have labelled the "Direct Optimization to a TS (Berny) Method" is that this method is fairly straightforward to use. However, it typically requires a reasonable guess structure. This is because the potential energy surface may be significantly different at points far away from the transition structure. Fortunately, the guess structure used in this study was suitable enough for this method to be used successfully.

The advantage of the method we have labelled the "Frozen Coordinate Method" is that it does not necessarily require the full Hessian to be computed - which may save us significant computational time. This is because differentiating along the unfrozen reaction coordinate may yield a sufficiently suitable guess Hessian.

Optimising Boat Transition Structure

Method Used

In this part of the investigation, we attempt to locate the boat transition structure using two quadratic synchronous transit (QST) methods: QST2 and QST3.

QST methods use the approximation that coordinates of atoms in the transition state correspond to a point on a parabola connecting the geometries of the structures of the reactant and products. The QST method also assumes that the reaction considered is a single step reaction involving concerted motion of all atoms in going from reactant to product (If it was a multi-step reaction, what would the QST2 method give you? Would it be completely useless? João (talk) 12:00, 20 March 2015 (UTC)). For reactions that can be so categorized, such as the Cope rearrangement considered in this investigation, this method is very powerful. The QST method then analyses the computed paths from the reactants to the products for a transition state.

The QST2 method requires ones to specify the reactant and product as inputs. The QST3 method requires one to specify the reactant, product and an initial guess transition state structure as inputs. We use the optimised Anti 2 conformation as our reactant and product structures. We relabel atoms in the product to ensure that the atom labeling in the products accounts for the Cope rearrangement.

Results & Analysis

Problem Encountered:

On the first attempt to locate the boat transition structure, we actually find the chair-like transition structure (except it is a bit more dissociated).

Table 9: Initial Reactant and Product Inputs in QST2

Atom Numbering Scheme used for Reactant	Atom Numbering Scheme used for Product	Chair-like Transition Structure Located through QST2 calculation

We can see that during the interpolation between the two suggested structures for the reactants and products in the QST2 calculation, only translation of the allyl fragments was attempted (rotation was not considered). We understand that for the QST2 calculation to locate the boat transition structure, we must modify the reactant and product input structures to resemble the desired boat transition structure more closely. This is done by modifying the central C2-C3-C4-C5 dihedral angle in the reactant and product to 0 degrees and changing the inside C2-C3-C4 and C3-C4-C5 angles to 100 degrees.

Table 10 shows the final input structures used in the QST2 calculation:

Table 10: Final Reactant and Product Inputs in QST2

Atom Numbering Scheme used for Reactant	Atom Numbering Scheme used for Product
	Numbering Scheme used in Modified Structure: Reactant

Table 11 summarises the results of the two methods used to optimise to the boat transition state structure:

Table 11: Optimised Boat Transition Structures using Two Methods

Method Used	Jmol Image	Energy (Hartrees)	Point Group Symmetry	Imaginary Vibrational Frequency	Animation of Imaginary Vibration
QST2		-231.60280243	C2v	-840.00
QST3		-231.60280221	C2v	-840.06

Intrinsic Reaction Coordinate (IRC) Method

Methods Used

In this part, the Intrinsic Reaction Coordinate (IRC) Method is be used to predict which conformers of 1,5-hexadiene the optimised chair transition state connects. The method works by following the minimum energy path from the transition structure provided down to the local minimum (low energy conformation) on the potential energy surface. The method takes small steps (changes in geometry) along this path of steepest descent. Since the reaction coordinate is symmetrical (we are considered a rearrangement where the reactants and products are the same conformation as 1,5- hexadiene), we chose to compute the IRC in one direction only (forwards). We choose to compute 50 points along the IRC in our calculations and calculate the force constants "always" (at every point along the IRC). Although the IRC calculation converges after 47 points (it does not need the full 50) - we find we have not reached any of the the exact minimum geometries expected (the final structure, shown in Figure 6, does not exactly resemble any of the 10 low energy conformations located in the first part of this investigation - this is because the IRC calculation is not as sensitive as the optimisation calculation in locating a minimum (Although, if you look in the program's manual, there are ways to adjust this João (talk) 12:00, 20 March 2015 (UTC))). Thus, we optimise this final structure to locate our local energy minimum. We note that throughout the range of calculations, consistency was maintained in regards to the level of theory used (in this case, HF/3-21G).

Figure 6: Final Structure (before optimisation) after IRC Calculation: Chair Transition Structure

Results & Analysis

Table 12: Using IRC Method to locate local minima

Transition Structure Used	IRC Graph	Jmol Image	Conformer Label	Energy (Hartrees)	Point Group Symmetry	Frequency Analysis
Chair			Gauche 2	-231.69166702	C2	All positive (real) frequencies

Thus, in this case, we understand that the chair transition state is connecting Gauche 2 conformation structures.

Activation Energies

Method Used

The chair (through direct optimisation to TS (Berny) method) and boat transition states (through QST2 method) located in the earlier section were reoptimised at B2LYP/6-31G* level of theory. Frequency Analyses were carried out for the all of the chair TS, boat TS and Reactant (anti 2) structures obtained using the two different levels of theory for which this had not been done before. Thermochemical data was analysed for all of these structures. The activation energy of the reactant is calculated by taking the difference between the sum of electronic and zero-point energies between the TS and reactants at 0K (because there is no thermal contribution to energy at 0K) and by taking the difference between the sum of the electronic and thermal energies at 298.15K. The calculated values are compared to the experimental values of activation energy at 0K (described in the "Results Table" of the instructions-page wiki).

Results & Analysis

Table 13: Summary of Energies (in Hartrees) for Reactants and Transition States

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.61932215	-231.466698	-231.461338	-234.55693195	-234.414910	-234.408982
Boat TS	-231.60280243	-231.450923	-231.445295	-234.54307807	-234.402352	-234.396009
Reactant (anti2)	-231.69253528	-231.539539	-231.532565	-234.61171167	-234.469214	-234.461866

• 1 hartree = 627.509 kcal/mol

Table 14: Summary of Activation Energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.	% Difference from Expt. of HF/3-21G Data	% Difference from Expt. of B3LYP/6-21G* Data
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K	at 0 K	at 0 K
ΔE (Chair)	45.70838307	44.69558354	34.07624874	33.18518596	33.5 ± 0.5	36.4%	1.7%
ΔE (Boat)	55.60733754	54.76271043	41.95650676	41.32586021	44.7 ± 2.0	32.6%	8.2%

We understand that the geometries of the transition structures optimised using different levels of theory are reasonably similar, however the energies of these structures are markedly different as noted in earlier analysis in "Anti 2 Conformation - Optimising with HF vs DFT" (As mentioned before, comparison of energies in that section is not very meaningful. In this section however, the activation energy is a relative energy and this comparison is most relevant. João (talk) 12:00, 20 March 2015 (UTC)). We see that the activation energies calculated using computations that used DFT/B3LYP level of theory are much more accurate as these values are much closer to the experimental values.

Conclusion

In this section, we located the low energy conformations of 1,5-hexadiene and the "chair" and "boat" transition state. We found that the various conformations of 1,5-hexadiene are very close in energy. Our findings show the Gauche 3 conformation is the lowest energy conformation, but we cannot conclude with much certainty that is the global minimum due to the very small energy differences between our optimized conformations, varying results in literature, and limitations associated with the method used. Suggestions for future work would include calculations using the CCSD(T) method using a significantly larger basis set- this may be further help determine which conformation is truly the global minimum. (Some coupled cluster methods and larger basis sets are available in Gaussian, if you wish you can give these a try. João (talk) 12:00, 20 March 2015 (UTC))

Four methods in total were used to locate the two transition states and the IRC method was used to determine which two conformations were connected by the optimised chair transition structure.

Activation energies were found for the chair and boat transition structure using both levels of theory used in this section. We saw that the activation energies calculated using computations that used DFT/B3LYP level of theory are much more accurate as these values are much closer to the experimental values.

Diels Alder Cycloaddition

The Diels-Alder reaction is an example of a π⁴s + π²s pericyclic cycloaddition reaction between a diene and a dienophile to form a cyclohexene system. It is generally accepted that the reaction proceeds via a concerted mechanism through a single, cyclic transition state. In this section, we will explore two Diels-Alder reactions - the reaction between ethylene and butadiene (to form cyclohexene) and the reaction between cyclohexa-1,3-diene and maleic anhydride.

Figure 7: Diels Alder Reaction

Ethene + Butadiene Reaction

In this section, we attempt to locate the transition structure for this prototype reaction. We analyse the frequencies and MOs of the transition structure to try and understand the reaction mechanism and why the reaction is allowed or forbidden. Calculations are performed in AM1 and B3LYP and results using the two different levels of theory are compared.

Method Used

In this section, we perform calculations using the AM1 and B3LYP/ 6-31G* level of theory. The B3LYP level of theory has been explained previously.

The AM1 (Austin Model 1) method is a semi-empirical method based on the neglect of differential diatomic overlap integral approximation. NDDO (Neglect of Diatomic Differential Overlap) sums the two centre integrals for repulsions between a charge distribution on one centre and a charge distribution on another centre - for everything else, the zero differential overlap approximation is applied (most two-electron repulsion integrals are neglected). MNDO is an extension of NDDO which accounted for correlation effects from second order perturbation theory using parameters fitted from experiment. AM1 was created as an extension of the MNDO model to better account for repulsion of atoms at close distances (and involved re-parameterisation). Overall, thus, semi-empirical methods such as AM1 make many simplifying approximation for the numerous integrals involved in ab initio Hartree Fock calculations that are computationally expensive to solve. Many of these integrals are approximated by functions with empirical parameters. The advantage of using a semi-empirical method such as AM1 is that it is much less computationally expensive compared to ab initio methods and by virtue of utilising real experimental data, can often give very accurate results. Limitations of the method (due to approximations and neglected factors as discussed) include that it systematically overestimates the stability of alkyl groups and can represent geometries incorrectly.

The transition structure was optimised directly to a TS (using Berny method) from the guess structure. The guess envelope type transition structure was built by first building a bicyclo-system and then removing the -CH₂-CH₂- fragment, and then setting both the distances between the terminal ends of the butadiene and ethene fragments to 2.2 Angstroms.

The type of calculations performed in this section have all been performed, described and discussed before in the tutorial.

Results & Analysis

Optimised Transition Structure

We begin by locating the transition state by optimising directly to the transition state using the Berny algorithm.

Table 15 shows details of the guess structure used.

Table 15: Guess Envelope Transition Structure Geometry

Jmol Image	Atom Labeling	C5-C9 distance (Angstroms)	C7-C11 distance (Angstroms)
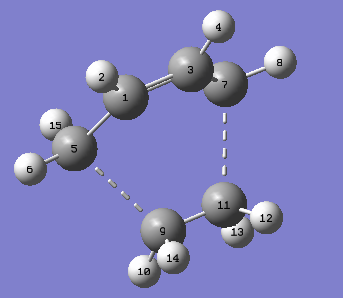		2.20000	2.20000

The tables below show the results of the optimised transition structure (frequency analysis confirms that we have located a transition structure). The bond lengths of the partly formed σ C-C bonds in the TS are given by C5-C9 and C7-C11 distances.

Table 16: Optimised Envelope Transition Structure Geometry

Method Used to Optimise to TS	Jmol Image	Atom Labeling	C5-C9 distance (Angstroms)	C7-C11 distance (Angstroms)
AM1		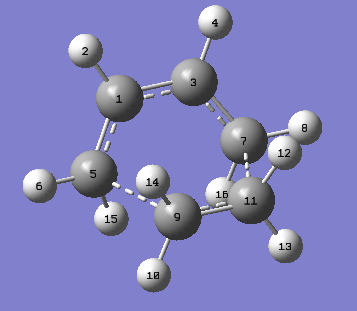	2.11924	2.11932
B3LYP/6-31G*			2.27155	2.27212

Typical C-C sp³ bond lengths are 1.54 Angstroms and typical C=C sp² bond lengths are 1.34 Angstroms. Therefore, we understand that the interactions between C5-C9 and C7-C11 cannot be classified as single or double C-C bonds. The Van Der Waals radius of Carbon is stated to be 1.7 Angstroms. The bond lengths of the partial bonds formed in the transition state (according to both levels of theory) are therefore less than twice the VDW radius of Carbon. This implies that there exists an attractive interaction between Carbons 5 & 9 and 7 & 11 respectively in the transition state which favours the formation of these bonds.

Table 17: Optimised Chair Transition Structures Analysis

Method Used	Jmol Image	Energy (Hartrees)	Point Group Symmetry	Imaginary Vibrational Frequency (corresponds to reaction path at transition state)	Lowest positive frequency
Semi-Empirical (AM1)		0.11165465	CS	Animation of Vibration with Imaginary Frequency of -956.17	Animation of Vibration with Lowest Positive Frequency of 147.35
B3LYP/ 6-31G* (DFT)		-234.54388560	CS	Animation of Vibration with Imaginary Frequency of -562.92	Animation of Vibration with Lowest Positive Frequency of 135.88

For both optimised structures, the frequency calculations gave one imaginary frequency. This means that at this point on the potential energy surface, the energy only falls in one direction (i.e. the reaction coordinate) and we have a transition structure. The motion exhibited in the vibration corresponding to the negative frequency shows how the reaction proceeds along the reaction coordinate via the transition state. We can see that the animated vibration for the negative frequency shows the synchronous bond formation of two new σ bonds (decrease in distance between C5-C9 and C7-C11 to form these fully defined single bonds explains why the energy falls in this direction Indeed, but bringing the fragments apart equally diminishes the energy. João (talk) 18:25, 20 March 2015 (UTC))). This synchronous bond formation supports the idea that the Diels-Alder reaction is a concerted pericylic process (where all bond breaking and formation occurs in the same, single step without generating an intermediate).

In contrast, the vibration with the lowest positive frequency does not involve the distance between the two fragments changing (all motion is perpendicular to inter-fragment axis). This is to be expected as this vibration has a positive frequency and is thus not associated with the reaction coordinate (along which we expect bond formation to take place). We can imagine that the "twisting" motion involved leads to a weaker HOMO-LUMO orbital interaction which may explain why energy rises through this motion away from the transition state.

Orbital Analysis

The Table below shows the HOMOs and LUMOs of the reactants and transition states optimised using the AM1 level of theory. In the table below, and further on this section, we describe orbitals as symmetric or anti-symmetric. This symmetry label refers to the symmetry of the orbital with respect to the reflection plane which bisects the molecule.

Table 18: HOMOs and LUMOs of the reactants and transitions states

	HOMO	LUMO
Ethene
Symmetry with respect to plane	Symmetric	Anti-Symmetric
Butadiene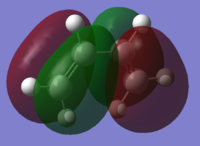
Symmetry with respect to plane	Anti-Symmetric	Symmetric
Transition Structure (AM1)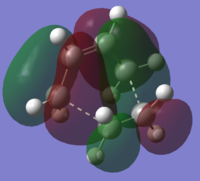
Symmetry with respect to plane	Anti-Symmetric	Symmetric

Below, we compared select molecular orbitals in the transition structures optimised using the different levels of theory. We don't compare the orbitals in the optimised reactants because the FMOs in the optimised reactants were found to be near-identical using the two different levels of theory.

Table 20: HOMO-1, HOMOs and LUMOs at transitions states using 2 methods

	HOMO-1	HOMO	LUMO
Transition Structure (AM1)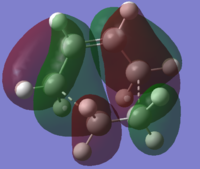
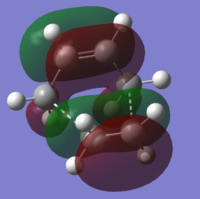
Symmetry with respect to plane	Anti-Symmetric	Symmetric	Symmetric
Transition Structure (B3LYP/6-31G*)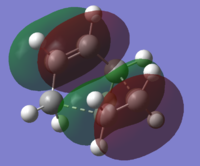
Symmetry with respect to plane	Symmetric	Anti-Symmetric	Symmetric

Allowed vs Forbidden

Orbital symmetry considerations are crucial in Diels-Alder reactions. Following the Woodward-Hoffman rules, the Diels Alder reaction can be said to proceed via suprafacial-suprafacial interactions of a 4π electron system (diene) and a 2π electron system (dienophile) which means it is thermally allowed as a 4n+2 cycloaddition.

In Diels Alder reactions, the π orbitals of the diene interact with the π orbitals of the dienophile to form the two new σ bonds. In this case, the relevant orbital interactions must be between π/π* (HOMO/LUMO) orbitals of ethene and the HOMO/LUMO orbitals of butadiene as shown in Table 15.

For sufficiently strong interaction between the HOMO of one fragment and the LUMO of another fragment and thus for the reaction to be allowed, there must be significant overlap density between the HOMO and LUMO. This is achieved when the two orbitals have the same symmetry properties and thus are primarily in phase with each other so a bonding interaction can result.

As denoted in Table 15, we can see that the HOMO of ethene and the LUMO of butadiene are both symmetric and the HOMO of butadiene and the LUMO of ethene are both anti-symmetric. Since both sets of interactions would involve orbitals with the same symmetry properties, the reaction is allowed.

FMOs at the transition structure

Using Frontier Molecular Orbital theory, we understand that a 'normal' electron demand Diels-Alder reaction primarily involves the interaction between the HOMO on the electron-rich diene and the LUMO on the electron-deficient dienophile. 'Inverse' demand involves the interaction between the HOMO on the sufficiently electron-rich dienophile and the LUMO on the sufficiently electron-deficient diene.

AM1 Transition Structure:

The HOMO at the transition structure is anti-symmetric. We can infer that this HOMO is a result of the interaction between the anti-symmetric HOMO on the diene (butadiene) and the anti-symmetric LUMO on the dienophile (ethene) as per a normal electron demand reaction.

AM1 vs B3LYP Transition Structure:

The calculated LUMOs (and most other orbitals) are the same using either method. In Table 20, we can see that the HOMO and HOMO-1 at the TS obtained via B3LYP corresponds to the HOMO-1 and HOMO respectively at the TS obtained via AM1 (the HOMO-1 with AM1/ HOMO with B3LYP looks like it is formed via interaction of HOMO of ethene and HOMO-1 of butadiene). Earlier, we have already observed that different methods may give slightly different optimised structures with different energies. We may thus understand that B3LYP yields a slightly different transition state with orbitals with different assigned energies and a different ordering.

Activation Energies

Table 20: Summary of Energies (in Hartrees) for Reactants and Transition States

	AM1 (Semi-Empirical)			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Ethene	0.02619027	0.077198	0.080252	-78.58745866	-78.536237	-78.533195
Butadiene	0.04878535	0.134631	0.139491	-155.98648555	-155.901144	-155.896442
Reactants Total (Ethene + Butadiene)	0.07497562	0.211829	0.219743	-234.5739442	-234.437381	-234.429637
Transition State	0.11165465	0.253275	0.259452	-234.54388560	-234.403327	-234.396905

• 1 hartree = 627.509 kcal/mol

Table 21: Summary of Activation Energies (in kcal/mol)

	AM1 (Semi-Empirical)	AM1 (Semi-Empirical)	B3LYP/6-31G*	B3LYP/6-31G*	Expt.	% Difference from Expt. of AM1 (Semi-Empirical) Activation Energy Value	% Difference from Expt. of B3LYP/6-21G* Activation Energy Value
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K	at 0 K	at 0 K
Transition State (Envelope)	26.00773801	24.91775488	21.36919149	20.53962459	22.8	-14.1%	+6.28%

Once again, we see that the B3LYP/6-31G* level of theory provides us with the more accurate value for activation energy.

Figure 8: Diels Alder Reaction

Cyclohexa-1,3-diene + Maleic Anhydride

In this section, we locate the reactants, transition structures and products involved in this reaction. Our analysis is mainly focused on trying to understand what our results say about possible selectivity associated with this reaction.

Results & Analysis

Optimised Reactants, Transition States and Products

We begin by locating the reactants, transition structures and products for this reaction. Given that the AM1 method was successful in yielding the expected orbitals in the preceding section, all calculations are carried out with AM1 level of theory in this section as well. Reactants and Transition were found by directly optimising guess structures (methods have been explained in earlier sections). Products were found by optimising the final structure given by IRC calculations (using the same method as in the Tutorial). Frequency analyses are conducted to confirm we have found local minima or transition states as required.

Table 22: Optimised Reactants

Reactant	Structure	Point Group Symmetry	Energy (Hartrees)	Frequency Analysis
Maleic Anhydride		C2v	-0.12182418	All positive (real) frequencies
Cyclohexa-1,3-diene		C2	0.02771129	All positive (real) frequencies

Table 23: Optimised Transition Structures

Transition Structure	Jmol Image	Energy (Hartrees)	Point Group Symmetry	Imaginary Vibrational Frequency	Animation of Imaginary Vibration
Exo		-0.05041984	CS	-812.32
Endo		-0.05150477	CS	-805.88

We can see that the animated vibration for the negative frequency shows the synchronous bond formation of two new σ bonds. This synchronous bond formation supports the idea that the Diels-Alder reaction is a concerted pericylic process (where all bond breaking and formation occurs in the same, single step without generating an intermediate).

Table 24: Using IRC Method to locate products

Product	IRC Energy Graph	Jmol Image	Energy (Hartrees)	Relative Energy (kcal/mol) Point Group Symmetry	Frequency Analysis
Exo		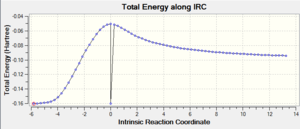	-0.15990937	0.16	CS	All positive (real) frequencies
Endo		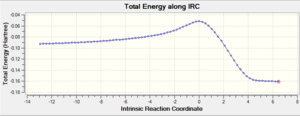	-0.16017069	0.00	CS	All positive (real) frequencies

For all the optimised structures, the energies (high for transition states, low for reactants and products), point groups and frequencies are as we expect.

We understand that our data indicates that the energies of the two products are very similar (near-identical) - so our data does not indicate one definite thermodynamic product (How does your energy difference compare with k_BT? João (talk) 18:25, 20 March 2015 (UTC)). In the following analysis, we will calculate activation energies and analyse orbitals to try and determine what our data indicates the kinetic product and then rationalise this finding.

FMO Analysis

Table 25: HOMOs and LUMOs of the reactants and transitions states

	HOMO	LUMO
Maleic Anhydride
Symmetry with respect to plane	Symmetric	Anti-Symmetric
Cyclohexa-1,3-diene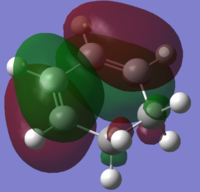
Symmetry with respect to plane	Anti-Symmetric	Symmetric
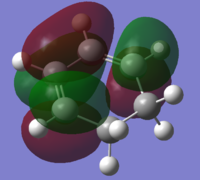
Exo Transition Structure (AM1)
Symmetry with respect to plane	Anti-Symmetric	Anti-Symmetric
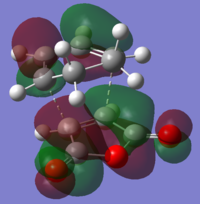
Endo Transition Structure (AM1)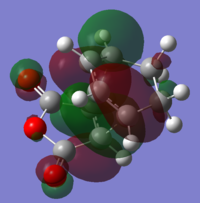
Symmetry with respect to plane	Anti-Symmetric	Anti-Symmetric

As shown in Table 25, we can see that the HOMO of maleic anhydride and the LUMO of cyclohexa-1,3-diene are both symmetric and the HOMO of cyclohexa-1,3-diene and the LUMO of maleic anhydride are both anti-symmetric. Since both sets of interactions would involve orbitals with the same symmetry properties, the reaction is allowed. The HOMO at the transition structure is anti-symmetric. We can infer that this HOMO is a result of a positive interaction between the anti-symmetric HOMO on the diene and the anti-symmetric LUMO on the dienophile as per a normal electron demand reaction. We may expect this reaction to proceed as a normal electron demand reaction seeing as we have an electron rich diene (alkyl groups in cyclohexa-1,3-diene are electron donating to the diene) and electron deficient dieonphile (-(C=O)-O-(C=O)- fragment with two carbonyl groups is electron withdrawing). The LUMO at the transition structure is also anti-symmetric, and we can infer that this LUMO is a result of a negative interaction between same two orbitals.

Analysis: Kinetics

Activation Energies

Table 26: Summary of Energies (in Hartrees) for Reactants and Transition States

	AM1 (Semi-Empirical)
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K
Maleic Anhydride	-0.12182418	-0.063346	-0.058192
Cyclohexa-1,3-diene	0.02771129	0.152502	0.157726
Reactants Total (Maleic Anhydride + Cyclohexa-1,3-diene)	0.07497562	0.211829	0.219743
Exo Transition State	-0.05041984	0.134881	0.144881
Endo Transition State	-0.05150477	0.133493	0.143682

• 1 hartree = 627.509 kcal/mol

Table 27: Summary of Activation Energies (in kcal/mol)

	AM1 (Semi-Empirical)	AM1 (Semi-Empirical)
	at 0 K	at 298.15 K
Exo Transition State	28.69284903	28.45565062
Endo Transition State	27.82186653	27.70326733

The results show that the endo transition state has a lower associated activation energy barrier. This implies the endo product will be the kinetic product. To try and understand why the endo transition state has a lower activation energy, we can consider relevant steric and electronic factors.

Steric Factors

The two tables below analyse the geometries of the two transition states located. We analyse the distances between the carbons in the -(C=O)-O-(C=O)- groups on the maleic anhydride fragment and the carbons atoms of the “opposite” -CH2-CH2- for the exo and the “opposite” -CH=CH- for the endo.

Table 28 shows details of the guess structure used.

Table 28: Exo Transition Structure Geometry

Jmol Image	Atom Labeling	C16-C19 distance (Angstroms)	C13-C20 distance (Angstroms)	C19-H17	C20-H14
		2.94499	2.94501	2.41622	2.41608

Table 29 shows details of the guess structure used.

Table 29: Endo Transition Structure Geometry

Jmol Image	Atom Labeling	C4-C19 distance (Angstroms)	C1-C20 distance (Angstroms)	C20-H5	C19-H6
		2.89150	2.89166	3.08277	3.08256

We can see that for both the structures, the distances between the specified carbon atoms are small (less than twice the VDW distance of C). We can understand that the proximity of the carbons (or the carbons on the maleic anhydride fragment to the hydrogens on the -CH2-CH2- fragment in the exo product) may result in a negative steric interaction. The distances between the carbons is smaller in the endo form - and we may infer that related steric repulsions are stronger in the endo form. However, in the exo form, the contact between the specified C atoms and nearby H atoms is much closer compared to the endo form. Overall, from this computational study, we cannot confidently state with certainty whether the exo or endo product would be more sterically congested. However, we can imagine that the close C-H contacts in the exo TS may help explain why the exo form has a higher activation energy.

Figure 8: Secondary Orbital Overlap Effect illustrated in HOMO-4 Orbital in Endo TS

Figure 9: Secondary Orbital Overlap Effect illustrated in HOMO-1 Orbital in Endo TS

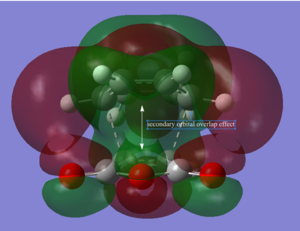
Electronic Factors

The stability of the endo transition state may be attributed to the stabilizing "secondary orbital overlap effects" - the name given to the interaction between the π systems of -CH=CH- and -(C=O)-O-(C=O)- fragments. To investigate the presence of this effect in our optimised structures , we visualised several occupied molecular orbitals (isovalue=0.01). We may interpret the HOMO-1 and HOMO-4 orbitals in the optimised endo structure to illustrate this effect:

We observe that the effect is apparent in the HOMO-4 orbital and we can infer that there may be a stabilizing effect due to an attractive interaction between the π systems of -CH=CH- and -(C=O)-O-(C=O)- in HOMO-1.

This stabilizing effect is only possible in the endo form (as the π systems of -CH=CH- and -(C=O)-O-(C=O)- fragments are close and near- parallel allowing the interaction to occur). This may also help explain why the distances between the C atoms specified in Table 28 and 29 were shorter for the endo form. We can understand that as the distance between the fragments gets shorter, the stabilising orbital interactions may become stronger but the sterics repulsions may become stronger as well. Therefore, an optimum distance would have to be reached to balance the effects of these two phenomena.

Overall, we can understand that secondary orbital overlap effects also may help explain why the endo form is calculated to have a lower transition energy.

Conclusion

In this section, we explored two Diels-Alder reactions - the reaction between ethylene and butadiene (to form cyclohexene) and the reaction between cyclohexa-1,3-diene and maleic anhydride. For both sets of reactions, the reactants, transition states and products were located.

Frequency analyses for transition states in both reactions illustrated synchronous bond formation and supported the idea that the Diels-Alder reaction is a concerted pericylic process (where all bond breaking and formation occurs in the same, single step without generating an intermediate).

MO analysis for both reactions also helped us rationalise why both reactions were allowed (Woodward-Hoffman rules).

For the reaction between cyclohexa-1,3-diene and maleic anhydride, we observed that the exo transition state had a lower activation energy. We can rationalise the results by considering steric and electronic factors (secondary orbital overlap effect). Our studies thus indicates that the endo product should be the kinetic product.