Rep:Mod:07966056076
Petr Ufimkin
Computational Experiment - Physical module - Transition structures
Introduction
The transition structures for the Cope rearrangement and the Diels Alder cycloaddition reactions were charactarized on potential energy surfaces in this assignment. GaussView 5.0 and Gaussian were used to do this.
Computational Method
Reactants, products and transition states can be optimized using various methods such as Hartee Fock and density functional theory (DFT), using a basis set such as 3-21G or 6-21G*. These optimizations solve schrodinger-like equations for each electron in a molecule in order to approximate the characteristics of said molecule.
A basis set is a set of functions that combine linearly to create molecular orbitals, the 3-21G and 6-21G* basis sets are Pople basis sets. The star after 6-21G* indicates that the set is polarized. Larger basis sets cover more of a molecule's molecular orbitals, and tend to yield more accurate results that incorporate more variables present in the molecule.
In mathematical terms the Hartee Fock (HF) method is:
The HF method involves the assumption that all the electrons in the molecule behave independently. In order to account for repulsions between electrons, each electron is considered to be affected by the average field of the other electrons, rather than considering each other electron as a separate entity. This means that electrons aren't correlated (unlike real electrons).
HF builds up a model starting from a hamiltonian, DFT takes this a step further by attempting to correlate the electrons. To do this, DFT adds a term for the exchange correlation (potential energy due to spin and charge) into an HF-like model, this can be done computationally because if the electron density of an electronic system is known, then in principle the energy can be found from it. There are multiple DFT methods, the one used in this project is B3LYP (B exchange functional, LYP correlation functional, and the 3 indicates the inclusion of some exact HF exchange).
Semi-imperical methods are also based on HF; they make more approximations, and are less expensive than HF. They use empirical parameters, and this allows partial inclusion of electron correlation effects. The AM1 semi-empirical molecular orbital method is the fastest used in this project.
These methods are used extensively throughout the assignment, to find data about both reactions, single molecules, and their behavior.
The Cope Rearrangement
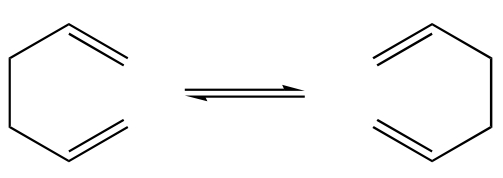
The Cope rearrangement is an intramolecular [3,3]-sigmatropic rearrangement, and is therefore both concerted and pericyclic. In this project the Cope rearrangement is of a 1,5-hexadiene, and can go through either a boat or chair transition state[2].
The Diels Alder Cycloaddition
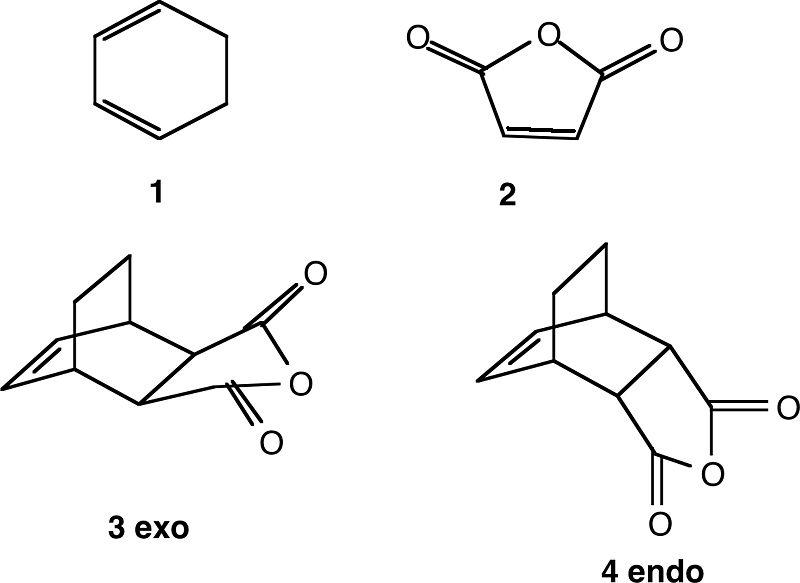
This reaction is a [4s+2s] cycloaddition, and is concerted and pericyclic like the Cope rearrangement, however not intramolecular. The reacting species and products in this example are (1&2 are reactants, 3&4 are products):
This reaction is stereoselective, in that either the endo or exo product can form. The endo product is kinetically favoured due to the secondary orbital effect. This arises from the favourable interactions between between the π systems of both the diene and dienophile (maleic anhydride), as they can approach each other closely in the endo transition state, making it less energetic and therefore take the reaction through a lower activation energy. The exo product is more stable and thermodynamically favoured due to having a less sterically hindered structure and the disapearance of the secondary pair effect in the reaction products.
Results and Discussion
The Cope Rearrangement Tutorial
JSmol diagrams of optimized structures are included at the end of each section, this excludes structures already represented visually in an alternate way.
Optimizing the Reactants and Products
1).a). Optimized a 1,5 - dihexane molecule with anti linkage at HF/3-21g level of theory, to give an energy of -231.69260236 Ha. Point group = C1.
b). Optimized a 1,5 - dihexane molecule with gauche linkage at HF/3-21g level of theory, to give an energy of -231.69266116 Ha. Point group = C1. This energy is lower than that for the molecule with the anti linkage; this is as expected, due to favorable orbital interactions and extra hydrogen van der waals contacts over weighing the effect of increased pauli repulsion energy in the gauche structure.
c). From the above results, I would assume that the lowest energy structure for 1,5-dihexane is a gauche one with the end carbons facing away from each other. This gives the same structure as in part b, with an energy of -231.69266116 Ha.
d). By looking at the energies of the structures I have optimized, and those in the appendix, it can be seen that the gauche structure is gauche3, and the anti structure is anti1.
e). Optimized a 1,5 dihexane molecule with anti2 configuration; this yielded an energy of -231.69253516 Ha, this is the same as in the appendix when rounded.
f). Optimized a 1,5 dihexane molecule with anti2 configuration by DFT at the B3LYP/6-31G* level, the symmetry remained Ci, whilst the energy increased to -234.61171062 Ha.
g). Ran a frequency calculation on the optimized molecule from f, at the same level of theory as in f; this yielded only real frequencies. The sum of electronic and zero point energies was -234.416259 Ha, the sum of electronic and thermal energies was -234.408966 Ha, the sum of electronic and thermal enthalpies was -234.408021 Ha, and the sum of electronic and thermal free energies was -234.447881 Ha.
| Optimized molecules: | |||||||||||||||
a).
|
b).
|
e).
|
f).
|
Optimizing the "Chair" and "Boat" Transition Structures
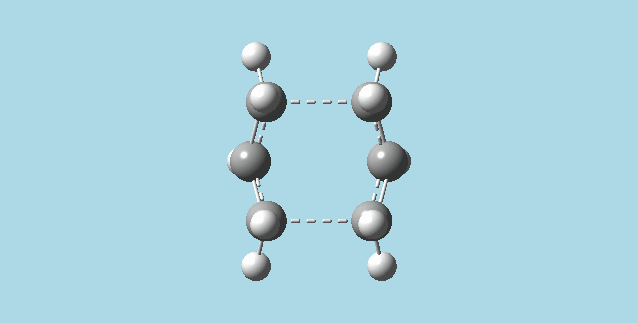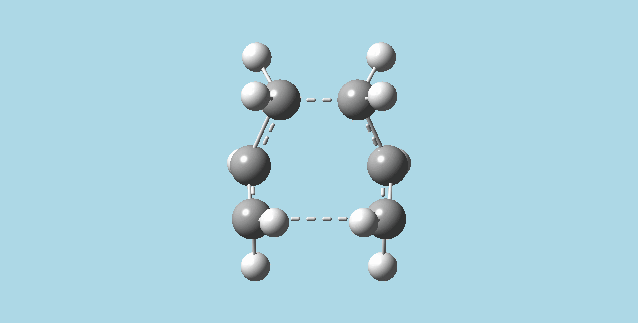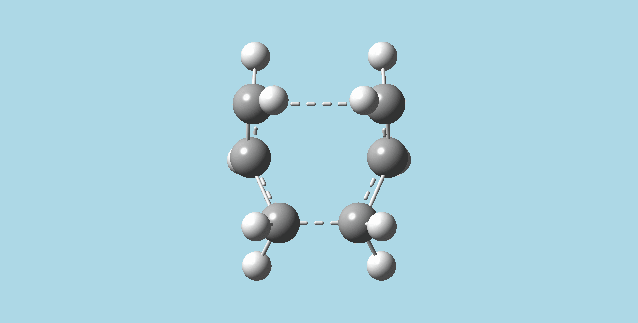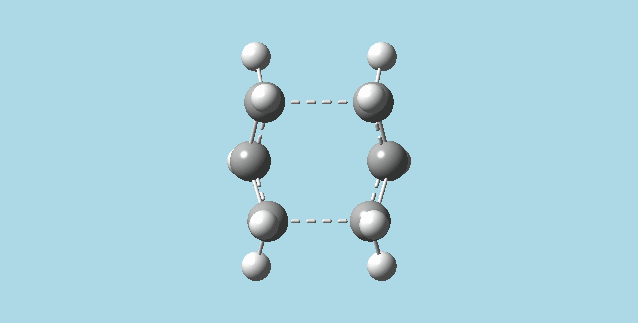
2). a). Optimized an allyl fragment using the HF/3-21G level of theory. Then placed two of these fragments together to make a guess model for the chair transition structure of the Cope rearrangement, with a 2Å distance between the molecules.
b). Did an optimization and frequency calculation on the guess chair transition structure above, at the HF/3-21G level of theory. The optimization was to a TS (berny), with force constants calculated once, and additional keywords, "Opt=NoEigen". The optimization gave a structure that corresponds to the one in appendix 2 for the Cope rearrangement chair transition structure. There was also an (imaginary) vibration frequency at -817.92 Hz which when animated corresponded to an asynchronous cope rearrangement mechanism.
c&d). Froze (as bonds) the terminal carbon atoms of each half of my guess chair conformation cope rearrangement transition state, with their corresponding terminal carbon atoms on the other half of the transition state using the redundant coord editor. Optimized at the HF/3-21G level of theory. Used the redundant coord editor to set the previously frozen carbons to be derivated. Optimized to a transition state (berny) at the HF/3_21G level of theory and Opt=NoEigen. This yielded a transition state where one of the bonds formed in the Cope rearrangement has a length of 2.01988 Å and the other 2.01969 Å. In comparison, the optimization from part 2)b had bond lengths of 2.02052 Å and 2.02074 Å.
e). Opened two anti2 1,5-hexadiene molecules (from 1)f) in two mol groups in one window. Changed the labels on carbons and hydrogens on both molecules, so as to make them correspond to the product and the reactant for the Cope rearangement (the atoms on the product were labeled to correspond to the same atoms in the reactant). Carried out an Opt+Freq calculation at the HF/3-21G level of theory, and TS(QST2). This job failed. Changed the dihedral angle between the central four carbons on both product and reactant to be 0°, and the angles between the carbons number 2,3, and 4 and the carbons 3, 4, and 5 to be 100°. Ran the Opt+Freq calculation with TS(QST2) again. This gives a boat transition state with an imaginary vibration frequency of -840.06 Hz, which animates like bond formation/breaking in asynchronous Cope rearrangement.
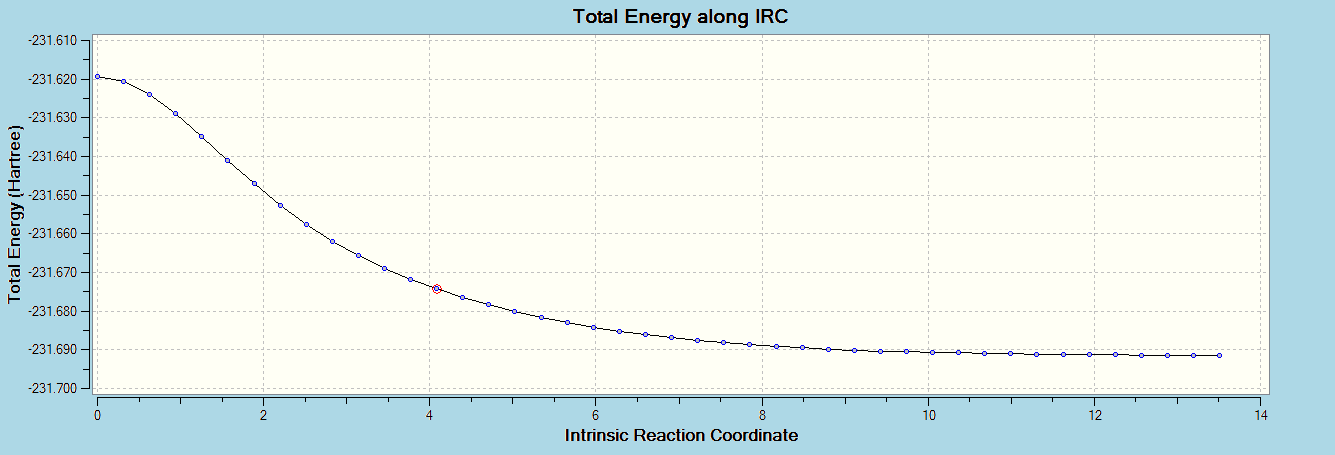
f). Opened the optimized chair transition state from part 2)b, and did an intrinsic reaction coordinate calculation in the forward direction, calculating force constants always, and with 50 points calculated along the IRC.
This animation and the graph below show a theoretically sound reaction coordinate.
i). Did an optimization at HF/3-21G for the last point of the IRC, getting the minimum geometry for the process. The point group for this molecule is C2.
ii). Repeated the IRC calculation for the chair transition state, but using 100 points for the calculation. The result for this calculation was identical to the original IRC, as expected, because the IRC stopped at point 44. No further IRC calculation was carried out, as the minimum has been reached.
g). Optimized to a TS (berny) (as in 2)b) and did a frequency calculation at the B3LYP/6-31G* level of theory on the optimized chair transition state from part b). The energies calculated from optimizations and recorded in this section (2)g) are for molecules at 0K.
The energy of this optimized transition state was -234.55698303 Ha. The reactant that forms this transition state is the gauche2 1,5-hexadiene, as this is the structure from the IRC minimum in f)i (the rearrangement is symmetrical, and therefore the product and reactant are the same). The energy of this reactant after B3LYP/6-31G* optimization is -234.61070157 Ha and its pointgroup is C2. This is a 0.03868676 Ha difference between the transition state and reactant, and this equals 33.7 kcal/mol (0.05371854Ha*4.35974434*10^-18J*6.0221413*10^23=141038.007686J/mol*0.239005736cal= 33708.8928309 cal/mol).
In comparison, the chair transition state optimized at the HF/3-21G level of theory yielded an energy of -231.61932224 a.u , and the IRC minimum reactant had an energy of -231.69166702 a.u and a point group of C2. This corresponds to an energy difference between the reactant and transition state of 0.07234478 Ha, which equals 45.3 kcal/mol, this is significantly different in energy from the activation energy calculated by DFT. Furthermore, the DFT activation energy is within the 33.5 ± 0.5 kcal/mol experimental activation energy range[5]. This increased accuracy is as expected from the higher level method. The geometries observed between the two methods however, haven't changed significantly.
Optimized to a TS (berny) (as in b) and did a frequency calculation at the B3LYP/6-31G* level of theory on the optimized boat transition state from part 2)e.
The energy of this transition state is -234.54309307 Ha. The reactant that forms this transition state is the anti2 1,5-hexadiene, as specified in 2)e, the energy of this reactant at the B3LYP/6-31G* level is -234.61171062 Ha (from 1)f), and its point group is Ci . This is a difference of 0.06861755 Ha between the transition state and reactant, and corresponds to 43.1 kcal/mol (0.06861755Ha*4.35974434*10^-18J*6.0221413*10^23*0.239005736cal=43058.1627734 cal/mol).
In comparison, the boat transition state optimized at the HF/3-21G level of theory yielded an energy of -231.60280240 Ha (from part 2)e), and the anti2 1,5-hexadiene had an energy of -231.69253516 a.u (from 1)e), and a point group of Ci. This is a difference of 0.08973276 Ha, which equals 56.3 kcal/mol, this is as before significantly different from the energy calculated by DFT. As before, The DFT energy falls within the experimental activation energy range of 44.7 ± 2.0 kcal/mol for a reaction progressing via the boat transition state (from script). This increased accuracy is as expected from the higher level method, the geometry of molecules doesn't change significantly between methods.
| Conformation and method | Energy with thermal correction at 298.15K/Ha |
| Chair HF/3-21G | (-231.461338) |
| Boat HF/3-21G | (-231.445302) |
| Chair B3LYP/6-21G* | (-234.424490) |
| Boat B3LYP/6-21G* | (-234.396008) |
As for the energies at 0K, the same pattern occurs where the chair transition state is more stable, and the B3LYP/6-21G* method gives significantly different values from the HF/3-21G. The energies have increased with the increase in temperature, as expected (molecules have more energy at higher temp), for example the boat transition state energy at the HF/3-21G level of theory has increased from -231.60280240 Ha to -231.445302 Ha, similarly the chair transition state energy at B3LYP/6-21G* increased from -234.55698303 Ha to -234.424490 Ha.
| Optimized molecules: | |||||||||||
a).
|
c&d).
|
f)i).
| |||||||||
g).
|
g).
|
g).
|
The Diels Alder Cycloaddition
3)a)i). Built cis-butadiene and optimized it by the AM1 semi-empirical molecular orbital method. Visualized HOMO and LUMO orbitals, and added a vertical reflection plane through the centre of the molecule:

|

| |
| HOMO - Asymmetric with respect to reflection plane. | LUMO - Symmetric with respect to reflection plane. |
ii). Optimized a guess transition state for ethene and a 1,3-butadiene from their diels-alder reaction. This was done by the AM1 semi-empirical orbital method, calculating force constants once, to a TS berny and with Opt=NoEigen. The transition structure obtained had a vibration at imaginary frequency -955.13 Hz:
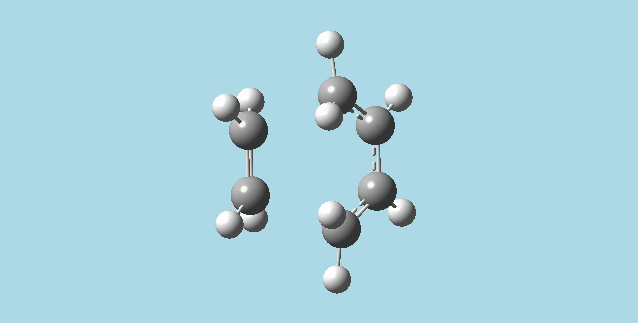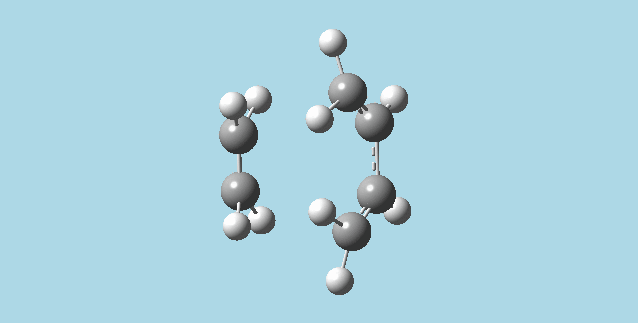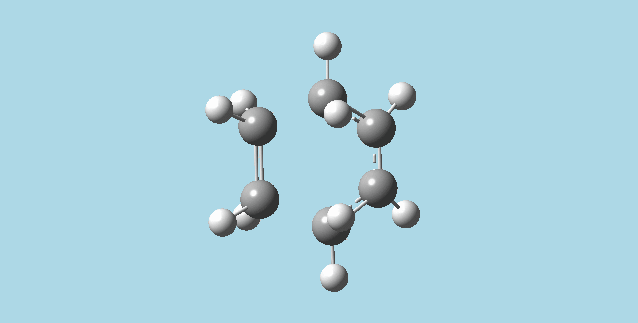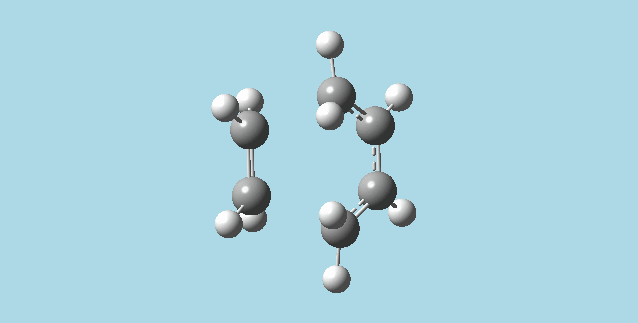
|
|
The formation of these bonds is a synchronous process. The lowest positive frequency for the transition state is 147.09 Hz, and has asynchronous vibration without a visible approach to reaction between the molecules.
The litterature sp3 C-C bond length is 1.54 Å, and the sp2 C=C bond length is 1.34 Å [6], both of these are lower than the 2.12 Å partly formed C-C bonds in the transition structure. The Van der Walls radius of the carbon atom is 1.7 Å [7], therefore under just Van der Waals interactions, two carbon atoms are spaced 3.4 Å away from each other. Therefore there is partial bonding character in the partially formed bond in the transition structure, as the distance between the carbons involved is less than what it would be under just Van der Waals interaction, and more than that under covalent bonding.
Visualized the transition state showing the HOMO and LUMO, with a reflection plane down the centre of the transition state:

|

|
| HOMO - Asymmetric. | LUMO - Symmetric. |
The Asymmetric nature of the HOMO with respect to the reflective plane implies that this orbital is formed from the cis-butadiene HOMO (asymmetric) and the ethylene LUMO (also asymmetric), as the reaction must be allowed and thus have orbitals of the same symmetry interacting. Looking at the above orbital visualizations, one can see that after constructive and destructive interference between the wave functions of each orbital, they form the HOMO orbital of the transition state. This overlap is the reason that the reaction is allowed.
iii). Optimized guess exo and endo transition structures for Cyclohexa-1,3-diene and maleic anhydride from their diels-alder reaction (with a 2.2 Å distance between reacting atoms). This was done by the AM1 semi-empirical orbital method, calculating force constants once, to a TS berny and with Opt=NoEigen. The lower level method was used in order to home in more rapidly on the transition state structure; this is useful as guessing a transition state structure takes multiple repeats.
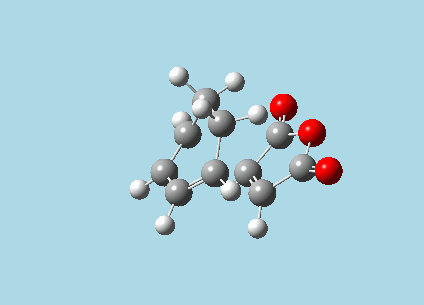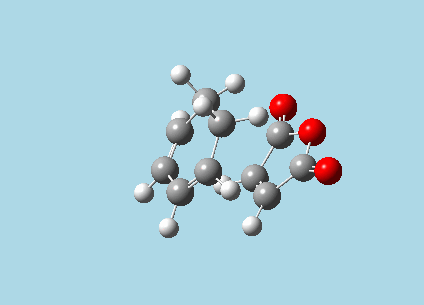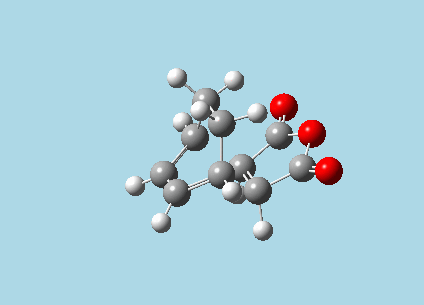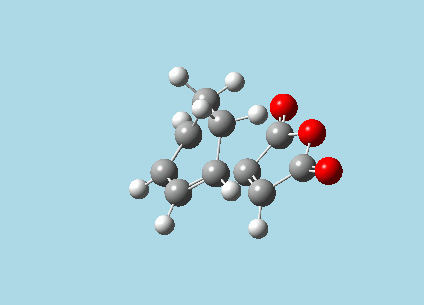
|
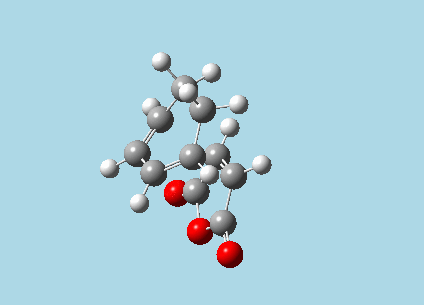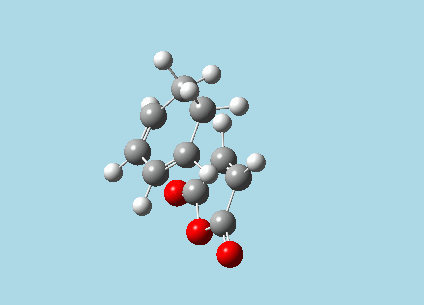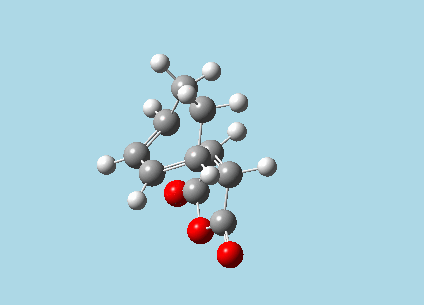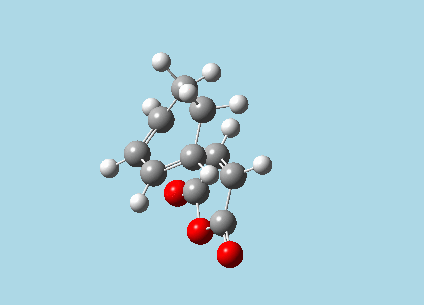
| |
| Exo-transition state with imaginary vibration frequency animation. | Endo-transition state with imaginary vibration frequency animation. |
Repeated the optimizations at the B3LYP/6-31G* level of theory, in order to get a more accurate value for the imaginary frequency and energy of the transition states. The geometries of the transition states didn't change with the changing method, however the original reactant bonds that were involved in the reaction became depicted as delocalized. The transition state energies at 0K and imaginary vibration frequencies for both optimization methods were:
| Geometry | AM-1 method energy/Ha | B3LYP/6-31G* methodenergy/Ha | AM-1 method imaginary frequency/Hz | B3LYP/6-31G* method imaginary frequency/Hz |
| Exo | (-0.05041984) | (-612.67931096) | (-812.33) | (-448.45) |
| Endo | (-0.05150469) | (-612.68339679) | (-806.30) | (-446.80) |
The endo form has lower energy than the exo form at both optimization methods. This lower transition state energy means that the reaction pathway forming the endo product has a lower activation energy and is therefore kinetically favorable. This is because molecules in the reactant are in a boltzman distribution of energies, and lowering the activation energy makes more of these molecules have enough energy to react. The secondary orbital overlap is the main cause of this, this overlap can be visualized on the HOMO of the transition state:

|

|
| Exo transition state HOMO. | Endo transition state HOMO. |
The endo transition state can be seen to have the parts of the HOMO formed from the dienophile's π system, approach close to the parts of the HOMO formed from the diene's π system (π systems don't come close in the exo form), this is a favourable interaction that stabilizes the transition state overall. However, these orbitals do not come that close together for the secondary orbital overlap, and therefore this effect is weak, it is likely that this is the reason why the energies of the endo and exo transition states are so similar.
|
|
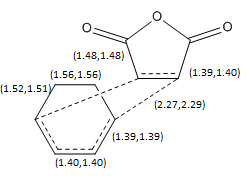
|
| Sketch of transition state without stereochemistry shown, bond lengths are in angstroms, and in brackets with the endo bond length first, and the exo second. |
The partial bonds formed in the transition state had higher lengths than any of the full bonding character bonds (2.27 Å for endo, and 2.29 Å for exo), this supports their partial nature, also they are still bonds as they are below the 3.4 Å[8] distance at van der waals interaction between carbon atoms. The other C-C bonds are approximately of the same length for both transition states. The double bonds appear to be delocallized across the transition state, mainly in the positions depicted as delocalized in the sketch, here the C-C distances are 1.40/1.39 Å and this is between the sp2 C=C bond distance of 1.34 Å [9], and sp3 C-C bond distance of 1.54 Å, implying a reduction in bond order from the double bond; the bonds that were originally single bonds also have a slight change from the sp3 C-C bond distance of 1.54 Å (1.52/1.48 Å) implying increased double bond character and therefore delocalization.
As the endo product is kinetically favoured, it is logical to predict that the exo will be thermodynamically favoured. The overall distance between the maleic anhydryde half of the transition state, and the cyclohexa-1,3-diene half is greater for the exo transition state (as can be seen from the JSmols above), this implies reduced steric hindrance for the exo form. Moreover, in the exo form the difference in the lengths between the bonds with depicted lengths in the above JSmols are greater (0.74 Å difference for exo vs 0.72 Å for endo), with a bigger angle making the maleic anhydryde group face away more from the -CH2CH2- group than the maleic anhydride group faces away from the -CHCH- group in the endo transition state. This reduces the amount of steric repulsion on the exo transition state, and this likely helps counteract the effect of the secondary orbital interactions, and keep the difference in energy between the transition states small. This geometry difference in the transition state implies a greater steric hindrance for the endo product aswell, compared to the exo product. This together with the greater Van der Waals forces in the exo product due to better overlap of the rings (due to geometry) and the disapearance of the stabilizing secondary orbital interactions in the endo product make the exo product more stable, and therefore the exo product the thermodynamically favoured one.
The effects of activating and deactivating groups as substituents on the diene/dienophile haven't been considered in this project. Changing an electron withdrawing group in conjugation with the alkene on a dienophile to an electron donating group can cause the reaction to go by inverse electron demand[10], where instead of being synchronous the reaction is asynchronous. [11]
- ↑ M.J Bearpark, QM3 Lecture Course
- ↑ O Wiest, K.A Black, K.N Houk,J. Am. Chem. Soc., 1994, 116 (22), pp 10336–10337
- ↑ M.J Bearpark, Experimental Script
- ↑ M.J Bearpark, Experimental Script
- ↑ M.J Bearpark, Experimental Script
- ↑ Advanced Organic Chemistry, 3rd Edition, F. A. Carey and R. J. Sundberg
- ↑ Van der Waals Radius of the elements, http://periodictable.com/Properties/A/VanDerWaalsRadius.v.html, November 2014
- ↑ Van der Waals Radius of the elements, http://periodictable.com/Properties/A/VanDerWaalsRadius.v.html, November 2014
- ↑ Advanced Organic Chemistry, 3rd Edition, F. A. Carey and R. J. Sundberg
- ↑ Carey, Part A., p. 839
- ↑ Boger, Dale (1989). Progress in heterocyclic chemistry (1st ed. ed.). New York: Pergamon. ISBN 978-0-08-037044-6.