Rep:Mod:07824559579

The Cope Rearrangement

The Cope rearrangement is a reaction of 1,5-dienes by a [3,3]-sigmatropic rearrangement.

Cope rearrangement showing boat and chair transition states

Cope rearrangement showing boat and chair transition states

It has been an area of extensive research for chemists with lots of computational and experimental efforts spent investigating its mechanism. Although the mechanism was controversial (either concerted, dissociated or step-wise) there is now substantial evidence to support a concerted mechanism for the rearrangement. Indeed, there are two possible transition structures; the boat and the chair.

The B3LYP/6-31G* level of theory has a good reputation for modelling enthalpies and activation energies for this system with striking similarity to experimentally determined values.

This paper delivers a concise report on the location of the transition structures and low-energy minima on the diene's PES to ultimately conclude with a preferred reaction mechanism for the Cope rearrangement.

Optimisation of an "anti" linkage 1,5-diene

Calculation Information	Anti 2	Gauche 1
Calculation type	FOPT	FOPT
Calculation Method	RHF	RHF
Basis Set	3-21G	3-21G
Final Energy (a.u)	-231.69253516	-231.68771617
RMS Gradient Norm (a.u.)	0.00004312	0.00000114
Dipole Moment (Debye)	0	0
Point Group	Ci	C2

Using GaussView, a molecule of 1,5-hexadiene was drawn in the "anti" conformation. This was cleaned (using the clean function) and the result optimised at the HF/3-21G level of theory. This product was symmetrised, to yield an anti conformer with C2 symmetry and an electronic energy of -231.69260. By comparing this conformer with literature, it was found to be the anti-1 conformer.

Optimisation of a "gauche" linkage of 1,5-hexadiene

The same method as above was applied to a drawn "gauche" formation of a 1,5-hexadiene molecule. In this incident another optimisation was required to identify the point group - found to be C2. The electronic energy was , and identified to be gauche-X.

It was predicted the anti conformer generated would have a lower energy as a consequence of there being less steric hindrance. Although in general the anti conformers are lower in energy than the gauche conformers, the lowest energy conformer is gauche 3 which is a surprise. It's minimum energy is thought to derive from an attractive interaction between an ethenyl proton and the pi orbital .

Comparison of HF/3-21G and B3LYP/6-31G* levels of theory for the Ci anti2 conformation of 1,5-hexadiene

The anti2 conformer was drawn by reproducing a jpeg illustration of the conformer as closer as possible. Molecular fractions were oriented by modifying their dihedral angles. At this stage the molecule was cleaned, and optimised for both levels of theory. The table on the right compares their respective output:

Calculation Information	Anti 2 HF/3-21G	Anti 2 B3LYP
Calculation type	FOPT	FOPT
Calculation Method	RHF	RB3LYP
Basis Set	3-21G	6-31G*
Final Energy (a.u)	-231.69253516	-234.61171020
RMS Gradient Norm (a.u.)	0.00004312	0.00001457
Dipole Moment (Debye)	0	0
Point Group	Ci	Ci

In comparison, the molecular geometries have not changed much. This point was determined by inspecting the bond lengths and bond angles using the 'modify bond' tool and 'modify angle' tool respectively. However, one significant difference is seen; the electronic energy result for the B3LYP/6-31G* level of theory is substantially lower for HF/3-21G. This is attributed to the complexity and significantly more accurate nature of the B3LYP/6-31G* level of theory. 6-31G* is recognised to be a more accurate than 3-21G as it incorporates polarisation and significant improvements for modelling core electrons.

anti2 3-21G

anti2 6-31G*

Frequency analysis of anti2 conformer

IR Spectrum most intense vibration B3LYP/6-31G* level of theory

A frequency calculation was carried out on the anti2 conformer under B3LYP/6-31G* level of theory. All the vibration frequencies were positive (no imaginary frequencies). This shows that this conformer has a local minimum electronic energy. The following spectrum was plotted from the computational values:

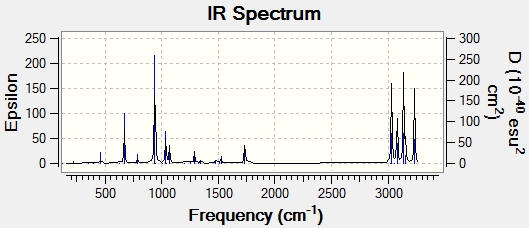
By accessing 'View file' from the results page the following thermochemistry data was retrieved:

Sum of electronic and zero-point Energies (a.u)	-234.469204
Sum of electronic and thermal Energies (a.u)	-234.461857
Sum of electronic and thermal Free Energies (a.u)	-234.500778

Locating the boat and chair transition states

An allyl fragment was drawn on Gaussview and optimised to using HF/3-21G level of theory.

Calculation Information	Allyl fragment HF/3-21G	Chair TS HF/3-21g	Boat TS QST2
Calculation type	FOPT	FOPT	FOPT
Calculation Method	RHF	RHF	RHF
Basis Set	3-21G	3-21G	3-21G
Final Energy (a.u)	-115.82304009	-231.61932247	-231.61932213
RMS Gradient Norm (a.u.)	0.00003834	0.00000833	0.00003967
Dipole Moment (Debye)	0.0291	0	0
Point Group	C2V	C1	C2H

The optimised fragment was copied and pasted twice into a new GaussView window. The fragments were oriented closely to the diagrams given. Using the bond tool, the terminal ends of the allyl fragments were adjusted to be approximately 2.2 Angstroms. And a TS (Berny) optimisation was calculated at HF/3-1G level of theory with the calculation of one force constant. "OPT=NOEIGEN" was added to prevent the calculation crashing when an imaginary frequency is detected.

An imaginary frequency of magnitude -817.92 cm-1 was recorded, confirming the existence of the transition state. The value agree nicely with the literature value -818 cm-1 (3sf).

Optimisation of the chair transition state by using the Frozen Coordinate Method

The bond lengths between the terminal allyl carbons was locked to 2.2 Angstrom by utilising the Redundant Coord Editor. A TS (Berny) optimisation at the same level of theory was run with the additional input of "OPT=MODREDUNDANT" as well as "OPT=NOEIGEN. This produced a similar transition structure as before but with the bond lengths fixed at 2.2 Angstrom.

optimised allyl fragment

First stage: lock bonds to 2.2A

TS from the Frozen Coordinate Method

Locating and optimising boat transition state

In this case, the QST2 method was used. This method finds the transition state by interpolating between specified reactants and products. Two The atoms in the starting 1,5-hexadiene were numbered to mirror exactly the same atoms following the rearrangement. In lieu of TS (Berny), TS(QST2) is used under HF/3-21G level of theory.

QTS2

Chair transition state animation at HF/3-21G level of theory

Boat transition state animation reached from the QST2 method

The imaginary frequency was found to be -840.01 cm-1, confirming the structure as the transition state.

Find below animations for both the chair and the boat transition states for the Cope rearrangement. From visual inspection, the characteristic boat and chair formations are are seen at the anti-node of the animations

Intrinsinc Reaction Coordinate method

IRC of guessed Boat transition structure (50 number of points). A minimum was reached prematurely

The Intrinsic Reaction Coordinate method (IRC) is a process in Gaussian that tracks the minimum energy path from a transition state through the local minimum on a PES. This is achieved by taking small geometry steps down the PES at its steepest point.

In this case, IRC was calculated in only the forward reaction because the reagent and product are symmetrical. The force constants were selected to calculate as "always". As the Boat TS was a guess, it was necessary to use a large number of points suitable to reach the local minimum. In this case, 50 number of points was used. It is important to note the calculation was substantially larger than any previously attempted optimisation.

On completion, it was apparent the TS had not been reached yet. In pursuit of the TS a normal optimisation under HF/3-21G level of theory was calculated. This method was chosen because it is the fastest option. If more time were available the force constant would be computed at every step.

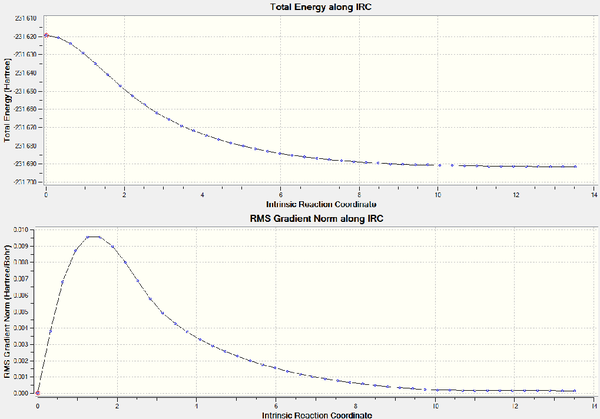
In this case, the local minimum was reached before the full 50 number of points had completed and so the calculation terminated at an earlier stage. The graphs were obtained under the results menu and selecting IRC path. They give confirmation that the energy minimum was indeed reached; both the 'RMS gradient norm' and the 'Total energy along IRC curve' have constant values for the last handful of data points. The steepest steps were at the 4th and 5th data point.

Determining activation energies using DFT/6-31G* level of theory

The activation energies for the boat and chair TS's were calculated using B3LYP/6-31G* level of theory. Once optimised, frequency calculations were executed.

Calculation Information	Chair TS	Chair TS/6-31G*	Boat TS 3-21G	Boat TS B3LYP/6-31G*
Calculation type	FOPT	FOPT	FOPT	FTS
Calculation Method	RHF	RHF	RHF	RB3LYP
Basis Set	3-21G	6-31G*	3-21G	6-31G*
Final Energy (a.u)	-115.82304009	-231.61932247	-231.61932213	-234.54504499
RMS Gradient Norm (a.u.)	0.00003834	0.00000833	0.00003967	0.00005950
Dipole Moment (Debye)	0.0291	0	0	0.1657
Point Group	C1	C1	C2H	C2H
JSmol	Chair TS after HF/3-21G optimisation	Chair TS after DFT B3LYP/6-31G* optimisation	Boat TS after HF/3-21G optimisation	Boat TS after DFT B3LYP/6-31G* optimisation

The same observations are noted here as BEFORE when comparing the different levels of theory; the geometries are very similar with only a marked difference in their electronic energies. Again, this is because of the enhanced accuracy of the B3LYP/6-31G* level of theory.

	Chair TS	Boat TS	Anti-2 conformer
Sum of electronic and zero-point Energies (a.u)	-234.469204	-234.40233	-234.46921
Sum of electronic and thermal Energies (a.u)	-234.461877	-234.39603	-234.46186
Sum of electronic and thermal Free Energies (a.u)	-234.500778	-234.43170	-234.50082

The activation energies were found by taking the difference between the relevant conformer (anti 2) electronic energy and the transition state electronic energies. By running frequency calculations at 0 K, the required electronic energies were determined to work out the activation energy at O K. Note: Gaussian automatically referred an input of 0 K back to the default 298.15 K. Therefore 0.1 K was used with success.

	Chair TS	Boat TS
Activation energy 0 K (kcal/mol)	34.056	41.961
Activation energy 298.15 K (kcal/mol)	33.105	41.322

As the product and reactant are the same across both TS's, only kinetic effects influence the reaction route. Therefore, the chair TS is the favourable reaction path. Any changes in thermodynamic conditions will all proceed with preference through the chair TS.

Diels-alder Reaction

The Diels-aleder reaction is a cycloaddition reaction. More specifically, it is a [4n+2] cycloaddition between a diene and a dienophile. A cyclohexene product is formed. Any Diels-Alder reaction is a concerted pericylic reaction.

Cope rearrangement showing boat and chair transition states

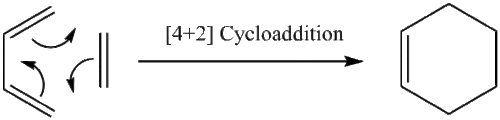
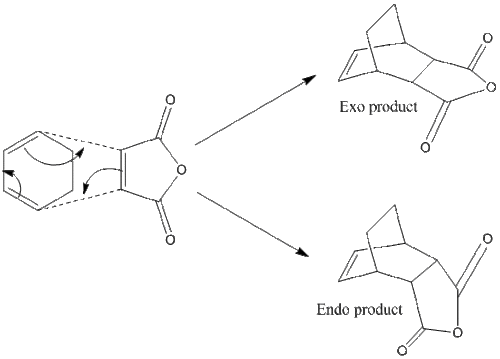
Diels-Alder reactions are stereospecific. When considering unsymmetrical dienophiles, the reaction proceeds through 2 unique transition states, the endo and exo. New bonds form from the overlap of π electrons forming stronger, sigma bonds. Frontier Molecular Orbital (FMO) theory would suggest the greater the orbital interaction between the dienophile's LUMO and the diene's HOMO, the greater the rate. Nevertheless, steric hindrance arising from a products structure is also an important consideration.

Transition state	Endo	Exo
Orientation in relation to diene π system	Towards	Away
Conditions for selectivity	Kinetic	Thermodynamic

This computational experiment addresses the transition state energies 2 reactions: The [4πS+2πS]cycloaddition of cis-butadiene and ethene, as well as the selective [4πS+2πS]cycloaddition of 1,3-cyclohexadiene and maleic anhydride. The transition states

Cis-butadiene + ethene

Cis-butadiene was created on GaussView 5.0, cleaned, and symmetrised initally with the AM1 semi-empirical MO method to hone towards the transition state. Once completed, a secondary optimisation using B3LYP/6-31G* level of theory was executed. The methodology of using a simpler level of theory first was chosen because it saves time.

The table below shows the results from the 2 optimisations.

Calculation Information	AM1 Cis-butadiene	B3LYP/6-31G* Cis-butadiene
Calculation type	FOPT	FOPT
Calculation Method	RHF	RHF
Basis Set	3-21G	6-31G*
Final Energy (a.u)	-115.82304009	-231.61932247
RMS Gradient Norm (a.u.)	0.00003834
Dipole Moment (Debye)	0.0291
Point Group	C2V
JSmol	Chair TS after HF/3-21G optimisation	Chair TS after HF/3-21G optimisation

The same optimisation method was carried out on ethene. The HOMO and LUMO molecular orbitals were visualised for both in GaussView.

Molecular Orbital	Visual	Symmetry with respect to the plane of symmetry
Cis-butadiene LUMO		Symmetric
Cis-butadiene HOMO		Anti-symmetric
Ethene LUMO		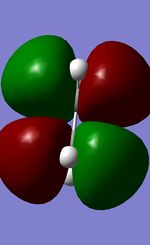Anti-Symmetric
Ethene HOMO		Symmetric

Computation of the transition state

The methodology chosen was to guess the transition structure and use a simple - AM1 semi-empirical MO method - level of theory followed by a more accurate - DFT B3LYP/6-31G* - model to determine the transition state. It is well established the TS has an envelope structure.Therefore a reasonable guess was made using the previously optimised ethene and cis-butadiene, and the calculations proceeded smoothly.

Calculation Information	TS AM1	TS AM1 followed by DFT
JSmol	TS AM1	TS DFT

After the optimisations were complete, a frequency calculation step was performed, yielding an imaginary frequency. This confirms the structure as a TS.

The average C(sp3)-C(sp3) and C(sp2)-C(sp2) bond length are reported to be 1.54A and 1.35A respectively. In contrast the TS bond length lies in between those specified previously, suggesting the 2 carbon atoms possess a bond order in between sp3 and sp2 hybridisation. This is further evidence to support this structure as TS because it suggests a transition. The carbon VDW radius is 1.70A. Two non-bonding carbons would have a distance of 3.40A. However the distance between the terminal carbons is significantly less than 3.40A, implying there is some degree of bonding occurring at the termini also. It is important to realise the concerted behaviour of the reaction, as seen in the animation below

Transition state for the reaction between ethene and cis-butadiene

Molecular Orbital discussion for cis-butadiene and ethene

As discussed already, the HOMO/LUMO of cis-butadiene must interact with the LUMO/HUMO of ethene for a successful Diels-Alder reaction to occur.

Maleic Anhydride and 1,3-cyclohexadiene

This is an unsymmetrical reaction, yielding both exo and endo products.

Cope rearrangement showing boat and chair transition states

Calculation Information	Maleic Anhydride	1,3-cyclohexadiene
Calculation type	OPT+FREQ	OPT+FREQ
Calculation Method	RB3LYP	RB3LYP
Basis Set	6-31G*	6-31G*
Final Energy (a.u)	-379.28968	-233.41838
RMS Gradient Norm (a.u.)	0.00008821	0.00003125
Dipole Moment (Debye)	4.034231	0.37776
Point Group	C2v	C2
JSmol	Optimised Maleic Anhydride	Optimised 1,3-cyclohexadiene

Molecular Orbital	Symmetry with respect to the plane of symmetry
Maleic Anhydride LUMO	Symmetric
Maleic Anhydride HOMO	Anti-symmetric
1,3-cyclohexadiene LUMO	Anti-Symmetric
1,3-cyclohexadiene HOMO	Symmetric

The Endo Transition State

The same optimisation approach was taken for this system as was used for the previous Diels-Alder reaction. Although the transition states were not guessed first time, the optimisation times were faster which was important in this case. If more time was available, it would be worthwhile to execute an IRC.

Endo-product Transition State

Homo -1 MO of the endo TS

Calculation Information	endo TS semi-empirical/AM1	Followed by DFT
Calculation type	FTS	FREQ
Calculation Method	RAM1	RB3LYP
Basis Set	ZDO	6-31G*
Final Energy	-0.05150479(RAM1)	-612.68339679 a.u.
RMS Gradient Norm (a.u.)	0.00000759	0.00001270
Dipole Moment (Debye)	6.1144
JSmol	Endo TS semi-empirical/AM1	Optimised Endo TS using B3LYP/6-31G*

The bond lengths for the optimised Endo TS under B3LYP/6-31G* level of theory are visualised in the JSmol above.

An imaginary frequency of -446.80 cm-1 was obtained for this transition state.

The Exo Transition State

Exo-product Transition State

Homo -1 of the Exo TS

Calculation Information	Exo TS semi-empirical/AM1	Followed by DFT
Calculation type	FTS	FREQ
Calculation Method	RAM1	RB3LYP
Basis Set	ZDO	6-31G*
Final Energy	-0.05150479(RAM1)	-612.67931096 a.u.
RMS Gradient Norm (a.u.)	0.00000759	0.00000526
Dipole Moment (Debye)	5.5503
Point Group	C1	C1
JSmol	Exo TS semi-empirical/AM1	Optimised Exo TS using B3LYP/6-31G*

For the exo TS, the imaginary frequency was determined to be -448.36 cm-1

Activation energies

	Chair TS	Boat TS
Activation energy 0 K (kcal/mol)	18.331	20.224
Activation energy 298.15 K (kcal/mol)	18.405	20.224

From obtaining the endo and exo transition state, it was possible to identify which was the kinetic product - the endo product. This is because its activation energy is lower than the exo-product's. This marked stabilisation is attributed to the secondary orbital overlap in the TS: At the endo TS, the new π bond interacts with the carbonyl orbitals on the maleic anhydride fraction because they have the same symmetry and are similar in energy. This interaction further stabilises the TS. The electronic energies of the products were very similar.

As a result, the endo product would be formed in higher yields than the exo product. This is supported by many literature reports.

Conclusions

The Cope rearrangement transition states were successfully reached and analysed to identify that the chair TS is lower in energy than the boat TS. As the product and reactant are the same across both TS's, only kinetic effects influence the reaction route. Therefore, the chair TS is the favourable reaction path.

For the Diels-Alder, the cis-butadiene and ethene reaction was analysed and its TS determined. Through MO analysis the symmetry conditions required for a Diels-Alder cycloaddition were shown to be true. Lastly the selectivity for the reaction between Maleic Anhydride and 1,3-cyclohexadiene was found to favour the endo-product by considering its lower activation energy. This is explained by a secondary orbital effect at the endo TS.

Looking forward, it would be interesting to computationally examine the relationship between the rate of cycloaddition and different intensities of HOMO-LUMO interaction for the dienophile and diene respectively.