Rep:Mod:01576020dp3618
Introduction
Gaussian was used to optimize the structures of several molecules using the RB3LYP calculation method and the 6-31G(d,p) basis set. Another calculation method was also used to explore its effects on the obtained results. The findings are discussed below. NH3, N2, H2, CO and SF4 were studied using the aforementioned program. Molecular orbitals of the latter molecule were also studied and discussed. Comparison to other studies of these molecules can also be found below.
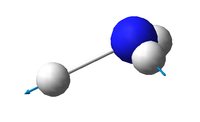
NH3 molecule
Optimisation
| Optimisation data | |
|---|---|
| Molecule | NH3 |
| File name | dp3618_nh3_optf_pop |
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -56.55776873 a.u. |
| RMS Gradient Norm | 0.00000485 a.u. |
| Dipole Moment | 1.8466 Debye |
| Point group | C3V |
N-H bond lengths: 1.02 Å
H-N-H bond angles: 106°
"Item" table:
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986275D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
NHmolecule |
The full optimisation .log file can be viewed here
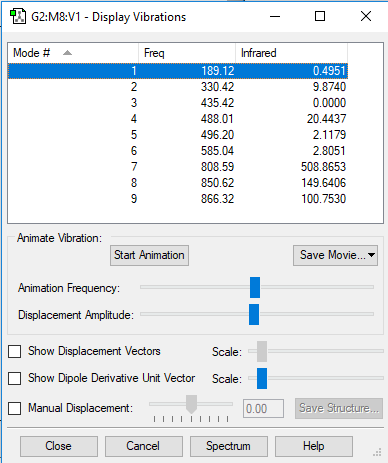
Vibrational analysis
| Vibration 1 | Vibration 2 | Vibration 3 | Vibration 4 | Vibration 5 | Vibration 6 | |
|---|---|---|---|---|---|---|
| Wavenumber [cm-1] | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| Symmetry | A1 | E | E | A1 | E | E |
| IR Intensity | 145 | 14 | 14 | 1 | 0 | 0 |
| Image |  |
 |
 |
 |
 |
|
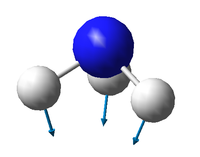
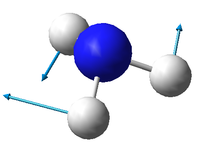
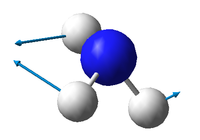
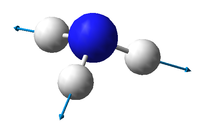
There are 3N-6 expected vibrational modes in a non-linear molecule. Since our molecule consists of 4 atoms, we would expect 6 vibrational modes to exist and that is confirmed by the quantum calculation.
There are 2 degenerate vibrational modes with a wavenumber of 1693.95 cm-1 and 2 degenerate modes with a wavenumber of 3589.82 cm-1.
Two types of vibrations exist; "bending" and "stretching". Vibrations with wavenumbers 1089.54 cm-1 and the two with 1693.95 cm-1 fall in the former category, whilst the other 3 fall in the latter. This is in agreement with the generally accepted fact that bending vibrations have smaller frequencies/wavenumbers than stretching vibrations.[1]
The stretching mode with the wavenumber 3461.29 cm-1 is highly symmetric.
The symmetric bending mode (1089.54 cm-1) is known as the "umbrella" mode.
Based on the calculated wavenumbers of the different vibrations, we would expect to see 3 bands in the experimental spectrum of gaseous ammonia (Vibration 4 is highly symmetric and therefore not IR active), but two of them are degenerate, so we only see 2 bands.
Predicted IR spectrum:
Charge analysis
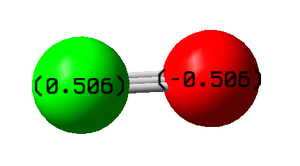
Taking into account the electronegativities of the constituent atoms of ammonia, we would expect the nitrogen atom to be negatively charged and the 3 hydrogen atoms to be positively charged. Since ammonia is neutral overall, the sum of the individual charges on atoms should be 0. This is confirmed by the results of the calculation.
The charge on the nitrogen atom is -1.125 and the charge on each of the hydrogen atoms is 0.375.
N2 molecule
Optimisation
| Optimisation data | |
|---|---|
| Molecule | N2 |
| File name | dp3618_n2_optf_pop |
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -109.52412868 a.u. |
| RMS Gradient Norm | 0.00000158 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point group | D∞h |
N-N bond length: 1.11 Å
"Item" table:
Item Value Threshold Converged?
Maximum Force 0.000003 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000001 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-2.352265D-12
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Nmolecule |
The full optimisation .log file can be viewed here.
Vibrational analysis
| Vibration 1 | |
|---|---|
| Wavenumber [cm-1] | 2457 |
| Symmetry | SGG |
| IR Intensity | 0 |
| Image |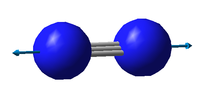 
|
There are 3N-5 expected vibrational modes in a linear molecule. Since our molecule consists of 2 atoms, we would expect 1 vibrational mode to exist and that is confirmed by the quantum calculation.
The vibrational mode is the "stretching" type and is symmetric.
There is no change in dipole moment and the molecule shows no bands in the IR spectrum, this is also predicted by our calculation (IR Intensity = 0).
Charge analysis
This molecule consists of two identical atoms with same electronegativities. We expect a purely covalent bond with charge 0 on both atoms. This is exactly what we see from the results of the calculation.
H2 molecule
Optimisation
| Optimisation data | |
|---|---|
| Molecule | H2 |
| File name | dp3618_h2_optf_pop |
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -1.17853936 a.u. |
| RMS Gradient Norm | 0.00000204 a.u. |
| Dipole Moment | 0.0000 Debye |
| Point group | D∞h |
H-H bond length: 0.74 Å
"Item" table:
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000005 0.001800 YES
RMS Displacement 0.000007 0.001200 YES
Predicted change in Energy=-1.634290D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Hmolecule |
The full optimisation .log file can be viewed here.
Vibrational analysis
| Vibration 1 | |
|---|---|
| Wavenumber [cm-1] | 4466 |
| Symmetry | SGG |
| IR Intensity | 0 |
| Image | 
|
There are 3N-5 expected vibrational modes in a linear molecule. Since our molecule consists of 2 atoms, we would expect 1 vibrational mode to exist and that is confirmed by the quantum calculation.
The vibrational mode is the "stretching" type and is symmetric.
There is no change in dipole moment and the molecule shows no bands in the IR spectrum, this is also predicted by our calculation (IR Intensity = 0).
Charge analysis
This molecule consists of two identical atoms with same electronegativities. We expect a purely covalent bond with charge 0 on both atoms. This is exactly what we see from the results of the calculation.
Structure and Reactivity
N2 molecule in a mono-metallic complex
An example of a mono-metallic TM complex coordinating an N2 molecule. Its crystal structure identifier is VEJROU. The structure was reported here.
Structure of the complex:
N-N bond distance in this complex is 1.20 Å, which is longer than the calculated N-N distance in the gas phase (1.11 Å). Some electron density which was used purely for bonding between the two nitrogens in the gas phase is now used to bond one nitrogen to the transition metal. There is less electron density between the nitrogens now, the bonding is weaker and longer. Since end-on N2 complexes are linear around the nitrogen, π backbonding can occur. In this case the d orbital of the metal atom can donate electron density into the π* orbital of the N2. The extend of this phenomena is dependent on the metal atom. If it is relatively electropositive, this effect is more significant, whereas in the case of more electronegative metals, such as Fe in our case, this is not so substantial.[2]
The values might also differ because of computational errors, these could be reduced by using a more accurate computational method. One should note, though, that there is also some error in the experimental data, due to instrumental or random errors.
Energy of N2(g) + 3 H2(g) -> 2 NH3(g) reaction
| Optimisation data | |
|---|---|
| E(NH3) | -56.55776873 a.u. |
| 2 * E(NH3) | -113.11553746 a.u. |
| E(N2) | -109.52412868 a.u. |
| E(H2) | -1.17853936 a.u. |
| 3 * E(H2) | -3.53561808 a.u. |
| ΔE = 2 * E(NH3) - [E(N2) + 3 * E(H2)] | -0.0557907 a.u. |
In the gas phase, the product of the above reaction is more stable than the reactants by 146.5 kJ/mol.
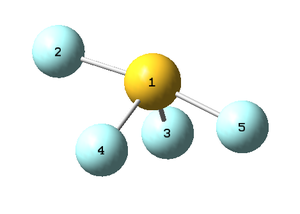
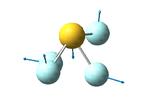
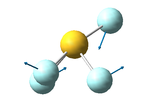
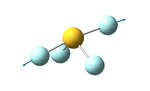
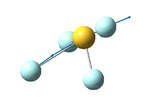
SF4 molecule
Optimisation
| Optimisation data | |
|---|---|
| Molecule | SF4 |
| File name | dp3618_sf4_optf_pop |
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -797.45952418 a.u. |
| RMS Gradient Norm | 0.00016003 a.u. |
| Dipole Moment | 0.8894 Debye |
| Point group | C2v |
Labeled picture of the molecule:
S-F(2 or 5) bond length: 1.67 Å
S-F(3 or 4) bond length: 1.59 Å
F(3)-S-F(4) bond angle: 102°
F(2)-S-F(5) bond angle: 171°
"Item" table:
Item Value Threshold Converged?
Maximum Force 0.000245 0.000450 YES
RMS Force 0.000136 0.000300 YES
Maximum Displacement 0.001150 0.001800 YES
RMS Displacement 0.000520 0.001200 YES
Predicted change in Energy=-5.227194D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.672 -DE/DX = 0.0002 !
! R2 R(1,3) 1.5946 -DE/DX = -0.0002 !
! R3 R(1,4) 1.5946 -DE/DX = -0.0002 !
! R4 R(1,5) 1.672 -DE/DX = 0.0002 !
! A1 A(2,1,3) 87.3127 -DE/DX = 0.0 !
! A2 A(2,1,4) 87.3127 -DE/DX = 0.0 !
! A3 A(3,1,4) 101.9122 -DE/DX = 0.0001 !
! A4 A(3,1,5) 87.3127 -DE/DX = 0.0 !
! A5 A(4,1,5) 87.3127 -DE/DX = 0.0 !
! A6 L(2,1,5,3,-1) 174.6253 -DE/DX = 0.0001 !
! A7 L(2,1,5,3,-2) 186.6353 -DE/DX = -0.0001 !
! D1 D(2,1,4,3) 86.6823 -DE/DX = 0.0 !
! D2 D(3,1,5,4) -102.0679 -DE/DX = -0.0001 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
SFmolecule |
The full optimisation .log file can be viewed here.
Vibrational analysis
| Vibration 1 | Vibration 2 | Vibration 3 | Vibration 4 | Vibration 5 | Vibration 6 | Vibration 7 | Vibration 8 | Vibration 9 | |
|---|---|---|---|---|---|---|---|---|---|
| Wavenumber [cm-1] | 189 | 330 | 435 | 488 | 496 | 585 | 809 | 851 | 866 |
| Symmetry | A1 | B1 | A2 | A1 | B2 | A1 | B2 | B1 | A1 |
| IR Intensity | 0 | 10 | 0 | 20 | 2 | 3 | 509 | 150 | 101 |
| Image |  |
 |
 |
 |
 |
 |
 |
|
|
There are 3N-6 expected vibrational modes in a non-linear molecule. Since our molecule consists of 5 atoms, we would expect 9 vibrational modes to exist. There are two vibrational modes with an expected IR intensity of 0 and there are no degenerate vibrational modes, so we would expect to see 7 peaks in an IR spectrum.
Charge analysis
This molecule consists of two types of atoms. Fluorine is more electronegative than sulphur, so we expect it to have slight negative charge. The charges on the two types of F atoms will probably be slightly different because of different bond lengths. This is exactly what we see from the results of the calculation.
Charge on sulphur is 1.983, charge on the closer two fluorines (3 and 4 in the above labelled picture) is -0.455 and on the two further apart (2 and 5) it is -0.537.
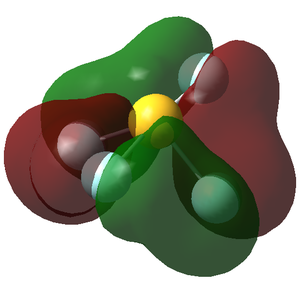
Molecular orbital analysis
MO 2
As can be concluded by looking at the visualisation of the orbital, the F atom s orbitals most likely contribute most to this molecular orbital (MO). This can be checked by inspecting the Molecular Orbital Coefficients in the .log file of the calculation. For this MO, the contribution of the S s atomic orbitals (AOs) is negligible, just as we would expect. Simmilarly, the other two F atom AOs do not contribute much towards this MO. The two 1s orbitals from two F atoms contribute most towards this MO, which is reflected in the size and shape of the orbital. This MO is very deep in energy and is therefore not involved in bonding.
MO 7
This orbital mostly has contributions from the sulphur AOs. It is almost entirely a 2px orbital, with very minor contribution from the other orbitals. It is also deep in energy, therefore it is a non-bonding orbital.
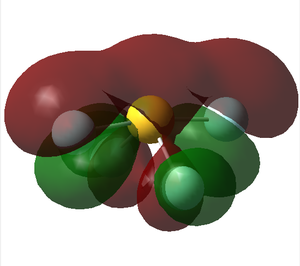
MO 10
This orbital is very interesting because it has relatively equal contributions from all atoms in the molecule. Another thing we notice when looking at the MO Coefficients is that this MO is almost entirely composed of 2s and 3s orbitals of all atoms. It is a bonding orbital.
MO 18
This MO has practically zero contribution from the s AOs. It is an antibonding orbital of the 2p and 3p fluorine AOs. Antibonding can also be noted by looking at the visualisation. There are 2 nodal planes going through the bonds.
MO 22
A MO composed of many AOs, mostly 2p and 3p AO of the fluorines and also 3p and 4pz AOs from the sulphur atom. This is a bonding orbital.
MO 26
Another very diverse MO, with substantial amount of anti-bonding character. It has many contributions from s and p orbitals of all atoms in the molecule. This MO is important because it is the highest occupied molecular orbital (HOMO).
MO 27
This is another anti-bonding orbital with many contributions from different AOs. It is the lowest unoccupied molecular orbital (LUMO) of this molecule. Since this is the lowest-lying MO, any electrons donated to this molecule will first occupy this orbital.
There is a gap in the MO energies between the 9th and the 10th. All MOs up to the 9th have energy lower than -6 a.u. These are non-bonding orbitals, which could also be concluded by looking at the visualisation of the orbitals since all of these are very localised to individual atoms. The 10th MO, on the other hand, is spread out over the whole molecule and has an energy value of -1.3 a.u. This orbital is therefore the lowest bonding orbital.
Independent work
Comparison of our results with other studies
An interesting study was carried out by Hay on the electronic structures of different sulphur compounds, including SF4, which was studied here.[3] That study took a different approach than ours, but the results are rather similar. The MO energies for example, are consistently slightly lower in our case, but all the trends coincide. There is a ~65 a.u. difference between the lowest and the second lowest orbital. These are followed by two pairs of degenerate orbitals. There is another substantial energy gap between the 5th and the 6th orbital. These similarities continue throughout the MOs.
Another study performed by Oberhammer et al. focused on the structure of chalcogen tetrahalides in the gas phase.[4] Their bond length results are in great agreement with our findings. The S-F bond lengths were 1.67 Å and 1.59 Å in our case and ~1.65 Å and ~1.55 Å in their. There was, however a difference in bond angles. Whilst ours were 102° and 171°, theirs were 87.5° and 101.5°. This is definitely something that should be further explored in the future.
Using different computational methods
NH3, N2 and H2 were also optimised using a different calculation method to explore what effect a different computational method would have on the outcome of the optimisation. The RCCSD-FC calculation method was suggested by a demonstator. There are very few differences between the two optimisations, probably owing to the simplicity of the molecules studied.
NH3 molecule The energy of the optimised structure was slightly higher in this second case at -56.39854662 a.u. The dipole was slightly higher, being 1.8637 D here. The N-H bond distance was 1.01 Å, which is slightly shorter than in the case of the RB3LYP calculation method. The H-N-H bond angle was the same at 106°. Vibrational frequencies were consistently higher by 40-80 cm-1. The full .log file can be viewed here.
N2 molecule In this case the energy of the second optimised structure was slightly higher at -109.25579376 a.u. N-N bond distance was the same as in the initial calculation. The vibrational frequency was slightly lower with 2411 cm-1. The full .log file can be viewed here.
H2 molecule Again, the energy of the optimised structure was slightly higher in the additional calculation, this time being -1.16515738 a.u. Bond length was the same, but the vibrational frequency was slightly higher: 4504 cm-1. The full .log file can be viewed here.
It is evident from the paragraphs above that the two methods used are very similar. They can therefore be used interchangeably in systems similar to the ones studied here. Perhaps the molecules used were not complex enough to invoke greater discrepancies in the results obtained.
CO molecule
Optimisation
| Optimisation data | |
|---|---|
| Molecule | CO |
| File name | dp3618_co_optf_pop |
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -113.30945314 a.u. |
| RMS Gradient Norm | 0.00001828 a.u. |
| Dipole Moment | 0.0599 Debye |
| Point group | C∞v |
C-O bond length: 1.14 Å
"Item" table:
Item Value Threshold Converged?
Maximum Force 0.000032 0.000450 YES
RMS Force 0.000032 0.000300 YES
Maximum Displacement 0.000011 0.001800 YES
RMS Displacement 0.000018 0.001200 YES
Predicted change in Energy=-3.956716D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1379 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
CO molecule |
The full optimisation .log file can be viewed here.
Vibrational analysis
| Vibration 1 | |
|---|---|
| Wavenumber [cm-1] | 2209 |
| Symmetry | SG |
| IR Intensity | 68 |
| Image |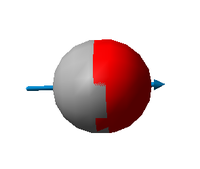 
|
Charge analysis
This molecule consists of two atoms with different electronegativities. We expect a dipole moment and two charges of opposite signs on carbon and oxygen. This is exactly what we see from the results of the calculation.
References
- ↑ Harwood, L. M., Claridge, T. D. W. (Eds.). (1997). Introduction to Organic Spectroscopy (pp.22-33). New York, Oxford University Press Inc.
- ↑ Holland PL. Metal-dioxygen and metal-dinitrogen complexes: where are the electrons?. Dalton Trans. 2010;39(23):5415-25.
- ↑ Jeffrey Hay, P. (1977). Generalized valence bond studies of the electronic structure of SF2, SF4, and SF6. 99. 1003-1012.
- ↑ Oberhammer H., Shlykov S. A., Gas phase structures of chalcogen tetrahalides MX4 with M=S, Se, Te and X=F, Cl, Br, I. Dalton Trans. 2010; 39: 2838-2841.
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 0.5/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES, overall very good however captions should always describe the item - captioning all of your jmols "molecule" is not helpful for the reader!
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES, overall very good effort with your explanations, well done. There are a couple of errors in your MO analysis, for example MO 18 is actually a bonding orbital of the F4 fragment (non bonding between S and F). The bonding interactions are through space between adjacent F atoms. There are nodal planes but these are along bonds, nodal planes indicating antibonding interactions are usually across the bonds.
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
Do an extra calculation on another small molecule, or
Do some deeper analysis on your results so far
You did extra calculations, analysis and comparison to the literature, well done!