Rep:Mod:0157274756701572747665

Introduction

Molecular mechanics and the MMFF94s force field used by ChemBio3D strives to obtain the shortest distance between all atoms in a molecule, to minimise the total energy of the system. It works on the assumption that all bonds are covalent and that the atoms are hard spheres for example the system would not be able to predict the energy of a 1,3-dicarbonyl species where an intra-molecular hydrogen bond is present. The hydrogen bond would not be accounted for by the system and the optimised structure would be different to the true conformation.

1,3-dicarbonyl system: An example where geometry optimisation is invalid

Dimerisation of Cyclopentadiene

Dimerisation of cyclopentadiene results in either the exo dimer or the endo dimer and is a bispericyclic reaction . The character of the reaction is dictated by both a π²s + π⁴s/π⁴s + π²s cycloaddition and also a [3,3] sigmatropic shift at the same time. 6 π electrons are involved in a thermal reaction therefore the transition state is Huckel and the reaction proceeds suprafacially with disrotaion of the frontier molecular orbitals. Therefore the reaction profile with the lowest transition state energy gives the endo product. Molecular mechanics will be used to see if this is also the thermodynamic product with the lowest total energy.The two structures were optimised using the MM2 forcefield in ChemBio3D. The breakdown of the energies of the Exo and Endo Isomer are given below.

Component	Endo Isomer Energies/ kcal mol-1	Exo Isomer Energies/ kcal mol-1
Stretch	1.2514	1.2848
Bend	20.8487	20.5796
Torsion	9.5102	7.6570
Van Der Waals	4.3188	4.2330
Total Energy	33.9975	31.8764

This is interesting as the thermodynamic product with the lowest energy is the exo isomer, contrary to the observed endo isomer. This proves that the reaction is kinetically controlled by the stability of the transition state. the Torsional strain is 1.8532 kcalmol^-1 higher in the endo isomer due to the closer proximity of the carbon framework and the repulsion of electron density of these bonds which is not observed in the exo isomer. Its is the Pauli repulsion of electron density in the bonds which raises the torsional energy in the endo isomer.

Hydrogenation of Cyclopentadiene

The subsequent hydrogenation of the endo dimer will determine the most stable position of the double bond, either in molecule 3 or molecule 4. The results are tabulated below:

Component	Molecule 3/ kcal mol-1	Molecule 4/ kcal mol-1
Stretch	1.2349	1.0965
Bend	18.9384	14.5243
Torsion	12.1238	12.4974
Van Der Waals	5.7289	4.5126
Total Energy	35.9266	31.1520

The question is whether the double bond is more stable in the 5 membered or a bridged 6 membered ring. The double bond position in molecule 4 leads to a thermodynamically more stable configurational isomer, with a lower total energy.

Optimised cyclohexene has an energy of 4.1920 kcalmol^-1 whereas optimised cyclopentene has an energy of 8.3115 kcalmol^-1 - however the bridging structure reduces the internal angle of the 6 membered ring compared to cyclohexene. It generates more strain as the alkene strives for an sp² angle of 120 degrees. This is confirmed by the bending energy being 4.4141 kcal mol^-1 higher in molecule 3 compared to molecule 4. This is the largest differing energy component. The Van Der Walls energy is 1.2163 kcalmol^-1 higher in molecule 3 than molecule 4, whereas other parameters are very similar.

Atropisomerism in an Intermediate Related to the Synthesis of Taxol

The objective is to determine which atropisomer has the lowest energy, where rotation about single bonds adjoining the carbonyl means that the two conformational isomers are also configurational isomers. The results below show 4 different energy minima for both the structure with the oxygen up and down. The cyclohexane ring can exist in both chair and both twist-boat conformers and this is also explored.

The results for mol. 9 Chair 1 mol. 9 Chair 2 mol. 9 Twist boat 1 mol. 9 Twist boat 2 are shown in the table below:

Molecule 9	Chair 1/ kcalmol-1	Chair 2/ kcalmol-1	Twist boat 1/ kcalmol-1	Twist boat 2/ kcalmol-1
Stretch	3.3218	2.7831	2.8772	3.6040
Bend	20.4823	16.5403	17.2864	20.6672
Torsion	22.0176	18.2588	20.6065	26.8394
Van Der Waals	14.9641	13.1124	14.3804	14.0741
Total Energy	58.3857	47.8396	53.0100	65.6338

It is interesting to note that the structure that contains 'twist boat 1' is lower in total energy than that containing 'chair 2'. On it's own, the chair is naturally lower in energy than the twist boat, however when incorporated into the taxol derivative, this is not true. The results for mol. 10 Chair 1 mol. 10 Chair 2 mol. 10 Twist boat 1 mol. 10 Twist boat 2 are shown in the table below:

Molecule 10	Chair 1/ kcalmol-1	Chair 2/ kcalmol-1	Twist boat 1/ kcalmol-1	Twist boat 2/ kcalmol-1
Stretch	3.3140	2.6199	4.99403	2.8330
Bend	16.8110	11.3431	49.9548	12.9804
Torsion	20.1182	19.6726	22.2206	22.9767
Van Der Waals	13.7744	12.8751	22.2408	14.1190
Total Energy	52.5425	42.6830	95.5597	49.5133

Similarly 'twist boat 2' is more stable than 'chair 1'. However for both molecules 9 and 10, it is a chair conformer which prevails as the lowest energy atropisomer. Molecule 9 resides in it's lowest energy form at 47.8396 kcalmol^-1 whereas molecule 10 exists at 42.6830 kcalmol^-1.

An important controlling factor in the reactivity of alkenes is the stability of the resulting carbocation in the rate determining step. The level of sigma conjugation and thus stability of the carbocation intermediate controls rate of the reaction - this is invoked by Hammond's postulate and transition state theory where the lowest energy route is via the most stabilised transition state . The tertiary carbocation is more stable through orbital overlap than the secondary carbocation and this controls the regioselectivity and location of the positive charge. However the alkene reacts unusually slowly. It can be described as a hyperstable alkene, and this is a consequence of the bridgehead in the structure. The bond strain caused by the bridgehead means that the carbocation is not able to form a planer sp² configuration and this is known as Bredt's Rule. The rate determining step is the formation of the carbocation and this is fastest when the transition state is lowest in energy. This strained nature of the carbocation means that it is comparatively higher in energy.

The energy of the optimised tertiary carbocation of molecule 10 ('chair 2') was calculated:

Component	carbocation intermediate/ kcal mol-1
Stretch	4.5751
Bend	21.5204
Torsion	22.7786
Van Der Waals	14.1403
Total Energy	52.0081

The torsional strain and bending energies are high for the cation: this reflects the point that the bicyclic structure can never be planar. The energy is thus high and from Hammond's postulate the transition state is also high in energy.

Spectroscopic Simulation Using Quantum Mechanics

Molecule 17 and Molecule 18 were optimised and the resultsing energies are displayed below.

Component	Molecule 17/ kcal mol-1	Molecule 18/ kcal mol-1
Stretch	5.0044	4.9720
Bend	22.8402	18.5972
Torsion	20.9604	24.4369
Van Der Waals	15.7953	17.6770
Total Energy	63.9627	64.2212

It is interesting to note that the lowest total energies of the 2 conformers are almost identical, but their internal component energies differ. Analysing the structures shows that molecule 17 contains a chair conformation of the 6 membered ring and an envelope conformation of the 1,3-dithiolane. In molecule 18 the 6 carbon ring is in the twistboat form and the 1,3-dithiolane is in the envelope conformation. The chair conformation is expected to give the lowest energy however this is not the case. Torsional strain is 3.4765 kcal mol^-1 higher in molecule 18 than 17 whereas bending energy is 4.2430 kcal mol^-1 higher in 17 than 18. Stretching energy is 0.0324 kcal mol^-1 higher in 17 and Van Der Waals energy is 1.8817 kcal mol^-1 higher in 18. These differences are reflective of the different conformations of the cyclohexane ring in the two optimised structures. The proton and carbon-13 NMR of molecule 18 was analysed.

Proton NMR for Molecule 18

SVG

The Calculated NMR environments are compared with the literature values. For molecule 18, the proton-NMR was recorded on a 300MHz spectrometer in C₆D₆ , so this solvent was used as the computed reference. Results are displayed in the table below:

Atom numbers	Hnmr environment:lit./ ppm	Hnmr environment: computed/ ppm
25	5.21	5.29
47, 50, {48, 49}	3.00-2.70	3.32-3.12 (3.32, 3.22, 3.11)
{26,32},29,31,{36,40,35}	2.70-2.35	2.86-2.28 (2.86, 2.45, 2.40, 2.28)
23,{24,30},{28,33},{53,37}	2.20-1.70	2.09-1.68 (2.09, 1.97, 1.86, 1.68)
38	1.58	1.62
{44,43},27,51	1.50-1.20	1.50-1.35 (1.50, 1.42, 1.36)
42	1.10	1.16
{52,39,41}	1.07	1.06
{45,46}	1.03	0.97

The multiplicity and integration of peaks is expected to be identical to the literature however it is important to analyse the computed chemical shifts with reference to the literature as this will determine how far away the optimised structure is from it's natural conformation. The chemical shift reveals how shielded the environment is and thus how much electron density is in that region of the molecule depending whether the environment is lower or higher field in the literature.

• The alkene proton (atom 25) is expected at about 5 ppm due to the deshielding exerted by the olefin ring current. In the computed spectra it is lower field and is thus more shielded than in the literature. This may mean that it is closer to the electron density of the carbonyl oxygen, or the large electron cloud from the sulphur atoms in the computed molecule.

• Protons alpha to the a heteroatom are expected between 3-4 ppm, the second highest chemical shifts in the molecule. Protons 47 and 48 are alpha to sulphur 19 (on same face as carbonyl)whereas protons 49 and 50 are aplha to sulphur 22 (on opposite face to carbonyl). These pairs of protons are not degenerate due to proximity to influencing electron density in the molecule however protons 48 and 49 are degenerate in chemical shift. This is due to the C2 axis in the envelope conformation of the 1,3-dithiolane ring and their far proximity to other influencing atoms in the structure. They are more shielded than in the literature. Perhaps this is due to Gaussian calculating the impact of both sulphur atoms on each proton environment whereas in reality this is less influential.

• There are 2 protons alpha to the carbonyl oxygen and these feature at chemical shifts: 2.86 & 1.42 ppm respectively. The carbonyl oxygen is pointing down whereas and they are pointing up and thus are not in close spatial proximity. This explains there low chemical shift. They are in good accordance with the literature.

• The general trend observed from the computed spectrum is that the chemical shifts are higher than the literature values. This is perhaps due to Gaussian overcompensating for electron density which in reality has little effect as it is too far away in the molecule.

Carbon NMR for Molecule 18

SVG

The 13C NMR from the literature were run on a 75 MHz spectrometer. Molecule 18 was dissolved in C₆D₆ , as before this was used as the reference solvent. The results are tabulated below:

Atom Number	environment lit./ppm	Computed environment/ ppm
10	211.49	211.73
2	148.72	148.56
3	120.9	118.73
12	74.61	88.98
9	60.53	67.78
11	51.30	56.01
6	50.94	55.49
7	45.53	50.01
20	43.28	48.01
21	40.82	44.12
13	38.73	41.93
4	36.78	37.48
15	35.47	35.21
8	30.84	30.94
34	30.00	28.74
1	25.56	28.56
18	25.35	25.64
5	22.21	25.16
17	21.39	23.29
14	19.83	20.94

As expected the inductive withdrawal of electron density means that the carbonyl carbon (atom 10) is in the lowest field position. The effect of the alkene ring current decreases the field experienced by the olefin carbons (atoms 2 & 3) so they are also deshielded. These three chemical shifts are almost identical.

Carbon atom 12 is in between two sulphur atoms so is deshielded by the inductive withdrawal of electron density from the two sulphur atoms. However in the literature the chemical shift is reported as 14.37 ppm lower than the calculated value. This means that Gaussian is stating that their is less electron density in close proximity to this carbon than in the observed molecule in the literature.

In general the computed chemical environments are in good accordance with the literature.

Energies of Molecules 17 and 18

• Molecule 17 energetic analysis

Energetic Analysis of Molecule 17

DOI:10042/25946

• Molecule 18 energetic analysis

Energetic Analysis of Molecule 18

DOI:10042/25947

The Gibbs Free Energy is quoted in Hartree units and this is converted into kJ/mol where 1 H =2625.50 kJ/mol.

-	ΔG/ kJ/mol
Molecule 17	-4377200
Molecule 18	-4335900

Molecule 18 is slightly more stable, and this is expected from the values obtained when the molecules were optimised, where molecule 18 had a lower energy. The free energies are negative indicating stability.

Introduction: Part 2

The aim of this part of the investigation is to rationalise the formation of a particular configuration of the epoxide and it's formation from an asymmetric catalyst (Shi and Jacobsen Catalysts). A large enantiomeric excess will be generated of one enantiomer and the interactions of the substrate-active site, catalyst structure and the epoxide NMRs can be used to explain the formation. Investigative work will be undertaken on trans-Stilbene epoxide and 1,2-dihydronapthalene epoxide.

Crystal Structures of Catalysts

A search of the Cambridge crystal database was performed to find the crystal structures of the two pre-catalysts which were made it the laboratory. Oxidising agent was needed to activate both catalysts,, . Interactions in the structures were analysed .

Shi Catalyst: Molecule 21

Shi Catalyst stabilised anomeric C-O bonds

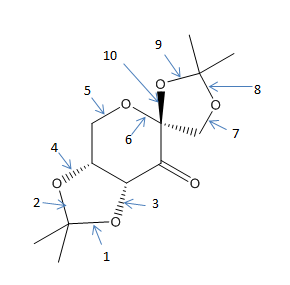
C-O bond from structure labels	Length/ pm	Potential for stabilisation by anomeric effect
1	145.6	Yes
2	142.8	Yes
3	141.5	No
4	143.7	No
5	143.4	No
6	141.5	Yes
7	142.9	No
8	142.3	Yes
9	145.4	Yes
10	142.3	Yes

Electron withdrawing groups α to the carbonyl activate the catalyst and the fused nature of the rings prevents epimerisation. The close proximity of the stereocentres to the carbonyl and subsequently the active dioxirane species allows for stereogentic communication, in the asymmetric catalytic stage. .

There are three anomeric centres in the molecule. The α-anomer of the 6 membered ring is stabilised by the donation of the oxygen lone pair into the C-O antibonding orbital. The structure was optimised in ChemBio3D and the oxacyclohexane ring adopts a boat conformation, this is the lowest energy conformer of the molecule, however for it to benefit from the stabilising anomeric effect, this 6 membered ring must be in the chair conformation. This highlights the point made in the introduction that hyperconjugative effects are not accounted for in structural optimisation in the MMFF94s force field used by ChemBio3D.

It is important to note that not all C-O bonds are stabilised by the anomeric effect, which arises from the donation of an oxygen lone pair in to a C-O antibonding orbital. Maximum overlap occurs when these orbitals are aligned in a syn-periplanar relationship. The C-O σ^* is a particularly good acceptor as it is low in energy and the lone pair is a good donor as it is high in energy and not restrained by another influencing nucleus.

C-O #6 is the shortest as expected as this is affected greatest by the anomeric effect. The oxacyclohexane ring is in the chair conformation allowing for excellent overlap of orbitals. The bond order is increased as the new NBO is of lower energy, there is more electron density between the C and O atoms and thus the bond is shortened.

The 5 membered ring containing C-O bonds: #1, #2, #3, #4 is in the half chair conformation. The overlap is better for C-O bond #2 than #1 illustrated by it's shorter bond length and #3 and #4 have no potential to be stabilised by the anomeric effect due to no adjacent C-O σ^*. It is interesting to note that #3 is particularly short, however not stabilised by the anomeric effect.

The other 5 membered ring is in the envelope conformation containing C-O bonds: #7, #8, #9, #10. #7 is not eligibly for stabilisation by the anomeric effect. The other 3 are. Interestingly there does not seem to be a correlation between the bonds which are eligible for stabilisation and their bond lengths: for example #7 is not eligible whereas #9 is but #7 is shorter than #9. This may be due to differing strains exerted by regions of the molecule on the C-O bonds.

Jacobsen Catalyst: Molecule 23

Jacobsen Catalyst: Molecule 23 crystal structure

Dispersion forces need to be considered for the isotropic H-H interactions between protons on the tert-butyl aromatic substituents. From the Lennard-Jones potential the maximum attractive distance between hydrogens is 240 pm where this is the sum of the two proton radii. This force becomes repulsive when the distance between protons is less than 210 pm. In Jacobsen's catalyst, there are 36 protons on tert-butyl groups, however the important interactions are between neighbouring tert-butyls on adjacent rings.

The molecule can be distinguished between having a concave face and the convex face, this allows an attractive force to occur where the distance between the protons is 233 pm between adjacent rings on the concave face and 258 pm on the convex face. There is a stronger interaction on the concave face. as 233 pm is closer to the optimal Van Der Waals radius for attraction.

It is important to note that the disymmetric character of the salene ligand is not present in molecule 23 when the complex is formed, but the complex is not planar. Similarly, the tert-butyl substituents on each phenyl ring are not aligned in the same manner as there is little attractive force between these protons.

The approach of the alkene is via the concave face, this narrows the channel of attack and the results in the stereoselctivity which will be discussed in the NCI part of the write-up.

NMR Analysis

The NMR spectra of the epoxides will be used as a precursor to the identifying the absolute configuration of the products, as they will ensure that the correct molecule is being computed when checked with the literature. Napthalene epoxide [R,S] proton-NMR spectrum was run on a 400 MHz spectrometer in CDCl₃ in the literature.

Proton-NMR

proton environment	Literature chemical shift/ ppm	calculated Chemical Shift/ ppm
17	3.68	3.94
16	3.80	4.29
18,	7.05	6.62
19,13,15	7.13-7.24	6.86-7.52
12,14	7.33-7.37	7.57-7.75

The computed spectrum above shows good accordance with the literature as all the environments are approximately in the same field region. The same comment can be made for the spectrum below.

Napthalene epoxide [R,S] carbon-13-NMR spectrum was run on a 100 MHz spectrometer in CDCl₃. Carbon-NMR

carbon environment	Literature chemical shift/ ppm	calculated Chemical Shift/ ppm
4	21.73	55.35
5	24.16	59.55
10	53.44	123.20
3	55.06	123.66
6	126.05	123.94
1	128.14	125.07
9	129.73	126.01
2	132.45	128.98
7	136.60	130.23

Environment #4,#5,#6 and #7 are not particularly close to the references values. These carbons are in close proximity to the heteroatom of the epoxide and they are more deshielded than what is observed naturally. Perhaps the optimisation did not generate the lowest energy structure.

Trans-Stilbene Epoxide [R,R] The proton-NMR was run on a 400 MHz spectrometer in CDCl₃ referenced to TMS in the literature and this was compared with the calculated spectrum where variables were kept the same.

proton environment	Literature chemical shift/ ppm	calculated Chemical Shift/ ppm
16,17,18,19,20,23,24,25,26,27	7.30-7.38	7.45-7.57
21, 22	3.87	3.54

The protons between7-8 ppm are aromatic and correlate well with the literature. They are slightly lower field perhaps due to Gaussian overcompensating the effect of the ring current.

The protons attached to the epoxide carbon are in the region expected for attachment to a heteroatom and are slightly higher field than the literature. The carbon-NMR was run on a 100 MHz spectrometer and again a CDCl₃ solvent was used referenced to TMS.

carbon environment	Literature chemical shift/ ppm	calculated Chemical Shift/ ppm
4,10	137.1	134.09
6,14	128.5	124.22
1,2,3,11,12,13	128.3	123.08-123.52
5,15	125.5	118.26
7,8	62.8	66.43

The C2 rotational axis in the epoxide means that all the chemical environments are paired. Again there is good correspondence between the calculated values and the literature.

Chiroptical Propeties of Epoxides

Gaussian used two wavelengths of light (589 nm & 365 nm) to generate the chiroptical propeties of the epoxide. The pre-recorded literature optical rotatory values were compared with the calculated values.

The optical rotation was measured for [R,R] trans-Stilbene epoxide and the results are given below.

wavelength	Calculated	Predicted from lit.
365	1254.00 deg
589	298.05 deg	250.8 deg

The optical rotation was measured for [R,S] 1,2-Dihydronapthalene epoxide and the results are given below.

Wavelength	Calculated	Predicted from lit.
365	935.74 deg
589	150.20 deg	145 deg

No literature values were found for the 365 nm wavelength however these will be useful for the experimental section as the spectrometer in the laboratory operates at this wavelength. Similarly the measurments were carried out at room temperature.

Transition state analysis for Shi Catalyst

The reaction is most likely to proceed via the lowest energy transition state. For alkenes 1,2-dihydronapthalene and trans-stilbene the free energy of the 4 lowest transition states on route to the (R,R)epoxide and again for the (S,S) epoxide were calculated. It is likely that the reaction will proceed via the lowest energy transition state under kinetic control, and this can be used to determine whether the R,R or the S,S is most likely to be formed in excess. The free energies are tabulate below: Stilbene

R,R TS free energy / H	S,S TS free energy/ H
-1634.687808	-1534.683440
-1534.687252	-1534.685089
-1534.700037	-1534.693818
-1534.699901	-1534.691858

1,2-dihydronapthalene

R,S TS free energy/ H	S,R TS free energy/ H
-1381.120782	-1381.131343
-1381.125886	-1381.116109
-1381.134059	-1381.126039
-1381.126722	-1381.136239

The difference between the lowest free energies of the two configurations {(R,R) and (S,S)} for each epoxide was analysed and the difference in free energy was calculated. The energy difference was first converted to kJ/mol for subsequent calculation. For stilbene the energy difference is 0.006219 H which converts to 16.327982 kJ/ mol. The equilibrium constant can now be calculated from the relationship Failed to parse (syntax error): {\displaystyle ΔG=-RTlnK} . The value of K is calculated as: 725.3596.

$x=K/(K+1)$ is used to calculated x where this is the enantiomeric excess and K is the equilibrium constant.

This translates to a value of 99.86% enantiomeric excess for the [R,R] configuration of stilbene oxide.

The same analysis is applied to 1,2-dihydronapthalene oxide. The energy difference between the 2 transition states is 0.00218 H and this converts to 5.723589 kJ/mol. The equilibrium constant K is calculated as 10.0632 which in this case translates to 98.30% enantiomeric excess for the [S,R] configuration.

Lowest energy [R,R] trans-stilbene TS This is formed in enantiomeric excess.

Lowest energy [S,S] trans-stilbene TS This is not formed in enantiomeric excess.

Lowest energy [R,S] 1,2-dihydronaphthalene TS This is not formed in enantiomeric excess.

Lowest energy [S,R] 1,2-dihydronaphthalene TS This is formed in enantiomeric excess.

It is possible to determine which face of the alkene will react with the catalyst by examining the geometry of the transition state. It is easy to see which dioxirane oxygen is used for the transfer from the transition state and is on the same face as the envelope ring, this is true for both enantiomers of the the precursor epoxide alkenes. There is an exo allignment of the alkene phenyl rings with the envelope rings of the catalyst, its is noted that orbital overlap is not perfect however this is a lower energy arrangemnet than the endo conformation as 4 electrons are involved in the frontier molecular orbitals, and the reaction will run via mobius topology; this conjecture was explored in the first section when the dimerisation of cyclopentadiene was explored. The mechanism of catalysis involves a spiro arangement of the trans-Stilbene epoxide and a distorted spiro allignment for 1,2-dihydronapthalene epoxide. The lone pair on the oxygen occupies an orbital of pi-symmetery and this is able to interact with the lumo of the alkene of the same symmetry. This tends towards the spiro geometry of the approaching alkene opposed to a planar arrangement as it has a stabilising influence.. A diagram is displayed below:

spiro and planar epoxidation geometries

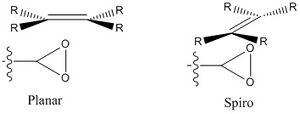
Formation of an S configuration involves attack of an electrophile to the Si face of the pro-chiral alkene and conversely formation of the R confiuguration involves attack from the Re face. For trans-Stilbene oxide a Re geometry is predicted and for 1,2-dihydronaphthalene a Si trajectory is implied. This is derived from the CIP notation.

Transition state analysis for Jacobsen Catalyst

The alkene cis-β-methyl styrene is subjected to the same analysis as for the Shi catalyst above.

1,2-dihydronapthalene

S,R TS free energy/ H	R,S TS free energy/ H
-3383.259559	-3383.251060
-3383.253442	-3383.250270

As before the energy difference between the most stable transition state for the [S,R] and [R,S] is calculated and the equilibrium constant is generated to see where the position of equilibrium lies for the formation of each enantiomer. A free energy difference of -22.314116 kJ/mol is calculated which gives a value of K = 8114.9160. This gives an enantiomeric excess of 99.99% for the [S,R] configuration.

[S,R] cis-β-methyl styrene: this is formed in enantiomeric excess.

[R,S] cis-β-methyl styrene: this is not formed in enantiomeric excess

This is just an example using the Jacobsen catalyst. There is a higher enantiomeric excess than for the Shi catalyst but meaningful comparions cannot be made as this is a different alkene substrate.

Non-Covalent Interactions of Transition State

The lowest energy transition state for the Shi Catalytic epoxidation of stilbene was subjected to a non-covalent analysis for the purpose of showing the regions of attraction and repulsion and explaining the selectivity of the catalyst for a particular enantiomer.

Orbital

Non-covalent interactions include, ion-ion/ ion-dipole/ dipole-dipole/ London forces interactions, Vand Der Waals interactions and hydrogen bonding and it is possible to analyse their effect upon the transition state, and any stabilising effect they might have on this high energy structure. From the animation a blue region indcated strong attraction, green is mildly attractive, yellow mildly repulsive and red being strongly repulsive. A qualitative description of the reacting system can elucidate which parts of the substrate and catalyst are interacting.

The transition state is the highest energy point on the reaction profile however the system is dominated by green mildly attractive interactions, these are distance dependent and result in Van Der Waals attractive forces where the sum of the atomic radii are reaching the energy minimum. whereas the high energy of the structure relates to the non-equilibrium bond lengths, which from the harmonic oscillator model are high in energy. strain of the bonds. The point of maximum attraction is the area of the oxygen approaching the double bond, this suggests that a bond is beginning to form. The oxygen atom is shrouded in a blue region. There is donation of electron density from the lone pair into the alkene antibonding orbital of the same symmetry and this is the beginning of the formation of an NBO which is of lower energy than the lone pair orbital on its own. This is consequently shown as a very favourable interaction for the catalyst-substrate complex. It is a very specifc arrangement where the oxygen is postioned exactly above the middle of the double bond to invoke maximum orbital overlap.

The alkene hydrogen also invokes an attractive Van Der Waals interaction

Electron withdrawing oxygen atoms are adjacent to the stereocentres of the five memeberd rings (the rings prevent epimerization od the catalyst and thus the product epoxide). Similarly bulky R groups are disfavoured by the planar geometry due to steric repulsions.

Electron Topology in the Active site of the Reaction Transition State

Shi Catalyst: transition state involving active site.

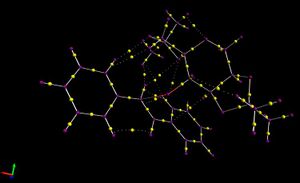
The yellow dots indicate the electron density within a bond where the purple dots are atoms. The imagine shows the approach of trans-Stilbene to the catalyst. It is noted that a covalent bond is forming between the dioxirane oxygen and the alkene and this is indicated by the red line on the diagram, however the electron density is still associated between the C-O bond of the catalyst, this interaction was invoked by orbital overlap earlier in the report.

From the NCI section above it was suggested that there was electron density existing on a surface between the the catalyst and substrate. This idea is reinforced in the electron topology model. The positive nuclei from both catalyst and substrate are alligned with electron density between the two structures which is attractive and holding the two structures in place and thus lowering the energy of the transition state. Unfortunately the distances were not measured as this would give a more conclusive idea of the strength of these interactions, judging by the corresponding Van Der Waals distances of the atoms involved.

suggesting New candidates for Investigation

The literature was searched to find an alkene which had previously successfully undergone assymetric epoxidation using either the Shi or Jacobsen Catalyst. Limonene had successfully undergone epoxidation using a variation of the Jacobsen catlayst. This molecule contains two doubles bonds however the chemoselectivity is 90% in favour of epoxidation of a particular double bond. In this project the interactions of the transition state were not analysed for the Jacobsen catalyst so this alkene would be a suitable candidate for computational analysis and comparison with the literature, it is reported as an [S,R] configuration in the literature.

Limonene Epoxidation

This product is commercially availbale from the Aldrich Catalogue as both laevorotatory and dextrorotatory with respect to the non-epoxide stereocentre. In the project molecules with a further stereocentre other than the epoxide component have not been analysed and the effect of another stereocentre in the molecule can be observed. The specific rotations are recorded as +69 degrees and -69 degrees..