Rep:Mod:01524069
NH3
NH3 optimisation: Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -56.55776873 a.u. RMS Gradient Norm = 0.00000485 a.u. Imaginary Freq = 0 Dipole Moment = 1.8466 Debye Point Group = C3V
NH3 3D rotatable image |
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
The N-H bond length = 1.01798 Angstroms and the H-N-H bond angle = 106°.
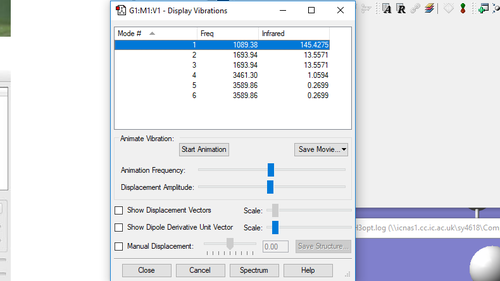
| Mode | Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image |
|---|---|---|---|---|
| 1 | 1090 | A1 | 145 | 
|
| 2 | 1694 | E | 14 | 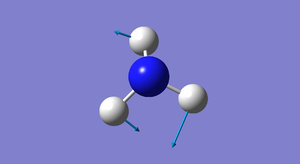
|
| 3 | 1694 | E | 14 | 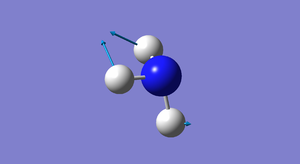
|
| 4 | 3461 | A1 | 1 | 
|
| 5 | 3590 | E | 0.3 | 
|
| 6 | 3590 | E | 0.3 | 
|
How many modes do you expect from the 3N-6 rule? From the 3N-6 rule, we expect to find 6 modes ( 3(4)-6=6 ). Which modes are degenerate (ie have the same energy)? There are 2 sets of 2 modes that are degenerate. The first set has a wavenumber of 1694 (modes 2 and 3) and the second set has a wavenumber of 3590 (modes 5 and 6). Which modes are "bending" vibrations and which are "bond stretch" vibrations? Modes 1,2 and 3 are bending vibrations and modes 4,5 and 6 are stretching vibrations. Bending a bond is easier than stretching it, so bending vibrations have lower energies than stretching vibrations. Which mode is highly symmetric? Mode number 4 (at wavenumber 3461) is a highly symmetric mode. One mode is known as the "umbrella" mode, which one is this? The "umbrella mode" is mode number 1 with a wavenumber of 1090. How many bands would you expect to see in an experimental spectrum of gaseous ammonia? There are 4 distinct sets wavenumbers so we would expect to see 4 bands in an experimental spectrum of gaseous ammonia.
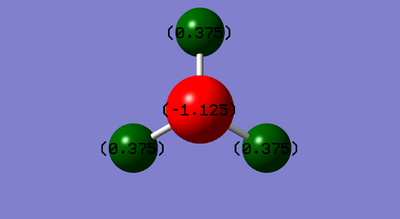
This charge distribution is expected as Nitrogen has a higher electronegativity than Hydrogen so has a stronger hold on the electrons in the bonds. Therefore, Nitrogen has a negative charge in terms of the charge distribution on the molecule.
The optimisation file is linked here
N2
N2 optimisation: Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -109.52412868 a.u. RMS Gradient Norm = 0.00000000 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = D∞h
N2 3D rotatable image |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
The N-N bond length = 1.10550 Angstroms with a bond angle of 180° as the molecule is linear.
| Mode | Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image |
|---|---|---|---|---|
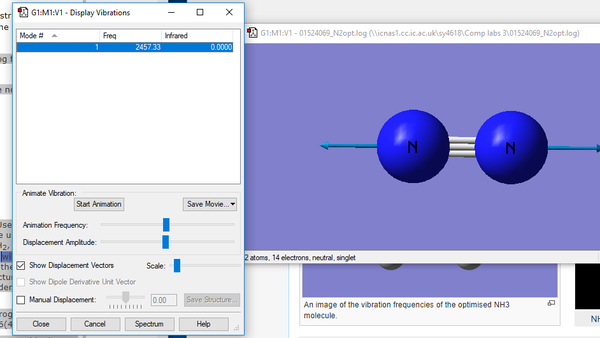
| 1 | 2457 | SGG | 0.0000 | 
|
The optimisation file is linked here
H2
H2 optimisation: Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = a.u. RMS Gradient Norm = 0.00000000 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = D∞h

H2 3D rotatable image |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
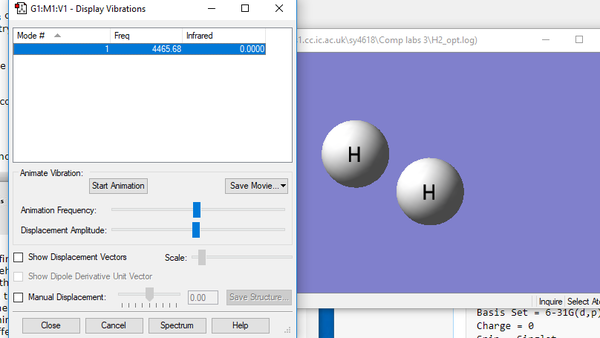
The H-H bond length = 0.74279 Angstroms with a bond angle of 180° as the molecule is linear.
| Mode | Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image |
|---|---|---|---|---|
| 1 | 4466 | SGG | 0.0000 | 
|
The optimisation file is linked here
AmmoniaːNH3
Ammonia is industrially manufactured bye converting nitrogen and hydrogen gas in the Haber-Bosch process for which the overall equation is shown belowː N2 + 3H2 --> 2NH3 E(NH3)= -56.55776873 a.u. 2*E(NH3)= -113.1155375 a.u. E(N2)=-109.52412868 a.u. E(H2)= -1.7853933 a.u. 3*E(H2)=-5.3561799 a.u. ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= 1.76477112 a.u. ΔE = positive 4633.4 kJ/mol This reaction is endothermic and so therfore the reactants are more stable as they are at a lower energy than the product.
Cl2
Cl2 optimisation: Calculation Type = FREQ Calculation Method = RB3LYP Basis Set = 6-31G(d,p) Charge = 0 Spin = Singlet E(RB3LYP) = -920.34987884 a.u. RMS Gradient Norm = 0.00000000 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = D∞h
Cl2 3D rotatable image |

Item Value Threshold Converged? Maximum Force 0.000094 0.000450 YES RMS Force 0.000094 0.000300 YES Maximum Displacement 0.000263 0.001800 YES RMS Displacement 0.000372 0.001200 YES
The Cl-Cl bond length = 2.04189 Angstroms with a bond angle of 180° as the molecule is linear.
| Mode | Wavenumber (cm-1) | Symmetry | Intensity (arbitrary units) | Image |
|---|---|---|---|---|
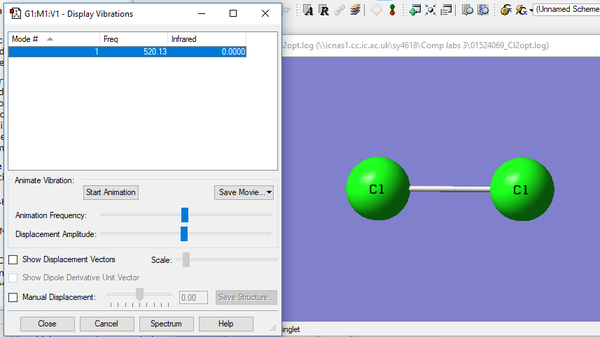
| 1 | 520 | SGG | 0.0000 | 
|
The optimisation file for Cl2 is linked here
Molecular orbitals
Cl2's homo is a 3π star antibonding molecular orbital (MO) in the x plane (shown in figure 1 below). It is the orbital in which the last electron has been placed. It's energy value is -0.31362. This MO is made up of 2 3p atomic orbitals and contains the maximum number of 2 electrons. As this is an antibonding orbital it has a negative effect on the bond order of the molecule. Cl2's lumo is a 3π star antibonding orbital in the z plane (shown in figure 2 below). This is the first empty molecular orbital that Cl2 has. It's energy value is -0.14211. This MO also is made up of 2 3p atomic orbitals. As the orbital is empty it will have no effect on the bond order of the molecule. Cl2's first MO is the 1σ orbital (shown in figure 3 below). It is made from 2 1s atomic orbitals. It is a bonding orbital that contains 2 electrons and therefore contributes positively towards the bond order of the molecule. it is very deep in energy. It's energy value is -101.60299. Even though the orbitals contributes to the overall bond order of the molecule, the atomic orbitals hardly overlap as they are held tightly near their nuclei so they are not very involved in the chemical bonding itself. The final two figures (figures ̩4 and 5 below) show the 3π bonding orbitals in the x and y plane. These two MO's are degenerate both with an energy of -0.40693. They were both made by the overlap of the 3p atomic orbitals. These orbitals are bonding orbitals and so they contribute positively to the bond order.
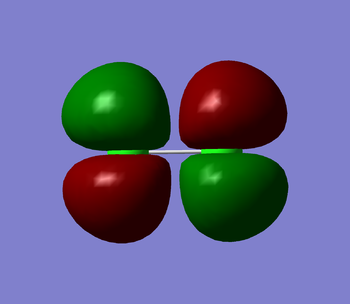



Marking
Note: All grades and comments are provisional and subjecct to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have recieved your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
Yes
NH3 0.5/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES - however instead of 4 bands only 2 bands are observed in the experimental spectrum of ammonia because the stretching vibrations are of very low intensity
N2 and H2 0/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES, you could have explained that the charges are 0 as the electronegativities are equal. You stated bond angles for H2 and N2. To determine a bond angle a minimum of 3 atoms is needed.
Crystal structure comparison 0/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
NO
Have you compared your optimised bond distance to the crystal structure bond distance?
NO
Haber-Bosch reaction energy calculation 0.5/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
NO - You used the right energies for the ducts and products. However the final result Is wrong.
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
NO
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES - even though you calculated the wrong number, you concluded a proper statement from this value.
Your choice of small molecule 4/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
You have done a good job of presenting this information, well done! You have stated a bond angle for a diatomic molecule, therefore the amount of achievable marks is lowered to 4.5. You could have explained the charges using an electronegativity argument. The MO in fig 3 is not a bonding one. You concluded the right way that there is no overlap. Therefore it is a non-bonding MO.
Independence 0/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far
NO
