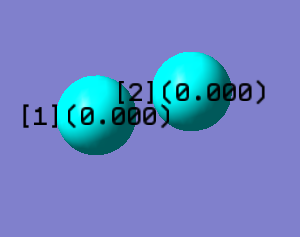NH₃, N₂ and H₂

NH₃ information

NH₃ parameters
Parameter	Value
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
E(RB3LYP)	-56.55777 a.u
RMS Gradient Norm	0.00000485 a.u
Point Group	C₃V
Optimised bond length (N-H)	1.02 Å
Optimised bond angle (H-N-H)	106°

NH₃ item table
Item	Value	Threshold	Converged?
Maximum Force	0.000004	0.000450	YES
RMS Force	0.000004	0.000300	YES
Maximum Displacement	0.000072	0.001800	YES
RMS Displacement	0.000035	0.001200	YES

Optimised NH

File:SIIMK NH3 OPTIMISATION FIRSTTEST.LOG

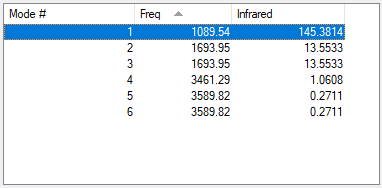
Vibrational frequencies of NH₃

Vibrations table for NH₃
Symmetry	A1	E	E	A1	E	E
Vibrational frequencies (cm⁻¹)	1090	1694	1694	3461	3590	3590
IR intensities	145	14	14	1	0	0
Images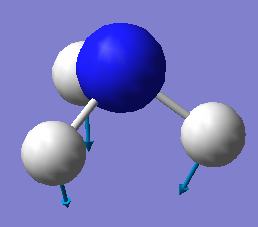

How many modes do you expect from the 3N-6 rule? There are 4 atoms in NH₃. Therefore N = 4. 3*4-6 = 6 modes.

Which modes are degenerate (ie have the same energy)? There are 2 degenerate bending modes at 1694 cm⁻¹ and 2 degenerate stretching modes at 3590 cm⁻¹.

Which modes are "bending" vibrations and which are "bond stretch" vibrations? Bending: 1090 cm⁻¹, 1694 cm⁻¹. Vibrations at higher frequencies correspond to bond stretch modes.

Which mode is highly symmetric? The stretching mode at 3461 cm⁻¹.

One mode is known as the "umbrella" mode, which one is this? The symmetric bending mode at 1090 cm⁻¹.

How many bands would you expect to see in an experimental spectrum of gaseous ammonia? 2 bands. One corresponds to the umbrella mode at 1090 cm⁻¹ and the other band to the bending mode at 1694 cm⁻¹. This is due to the fact that only these modes are predicted to be high enough in intensity to be visible. The stretching modes are orders of magnitude smaller in intensity and thus unlikely to be seen in the spectrum.

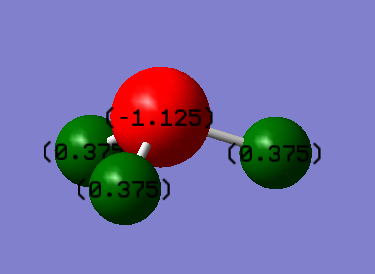
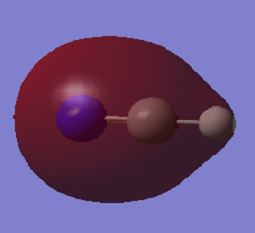
Charge distribution in NH₃

The red atom corresponds to nitrogen and green atoms are hydrogens. As nitrogen is more electronegative than hydrogen, N pulls electron density away from H atoms and obtains a negative charge as a consequence.

N₂ information

N₂ parameters
Parameter	Value
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
E(RB3LYP)	-109.52413 a.u
RMS Gradient Norm	0.00000060 a.u
Point Group	D∞h
Optimised bond length (N-N)	1.11 Å
Optimised bond angle (N-N)	180°

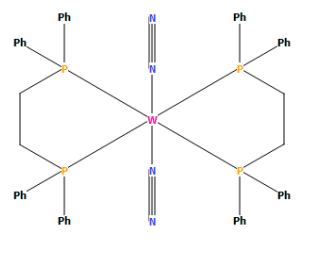
A wolfram complex with two N₂ ligands^[1]

N-N triple bond length in the wolfram complex is 1.127 Å as reported in the database of Cambridge Crystallographic Data Centre.^[1] The bond length in a free N₂ molecule was approximated to be about 1.11 Å using the Gaussian software. The bond length of N₂ in the complex is larger for to the reason that the wolfram atom withdraws electron density from the ligand (N₂). As a consequence, electron density on N₂ decreases, the bond weakens and bond length increases. Note that the two N₂ ligands are equivalent in the complex and N-N bond lengths are the same for both ligands.

N₂ item table
Item	Value	Threshold	Converged?
Maximum Force	0.000001	0.000450	YES
RMS Force	0.000001	0.000300	YES
Maximum Displacement	0.000000	0.001800	YES
RMS Displacement	0.000000	0.001200	YES

Optimised N

File:SIIMK N2 OPTIMISATION SECONDTEST.LOG

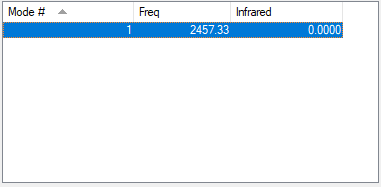
Vibrational frequencies of N₂

N₂ vibrations
Symmetry	SGG
Vibrational frequencies (cm⁻¹)	2457
IR intensities	0
Images

Charge distribution in N₂

Both atoms represented on the image are N atoms. For the electronegatives of both nitrogens are equivalent, the atoms bear no charges, as expected.

H₂ information

H₂ parameters
Parameter	Value
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
E(RB3LYP)	-1.17854 a.u
RMS Gradient Norm	0.00000017 a.u
Point Group	D∞h
Optimised bond length (H-H)	0.74 Å
Optimised bond angle (H-H)	180°

H₂ item table
Item	Value	Threshold	Converged?
Maximum Force	0.000000	0.000450	YES
RMS Force	0.000000	0.000300	YES
Maximum Displacement	0.000000	0.001800	YES
RMS Displacement	0.000001	0.001200	YES

Optimised H

File:SIIMK H2 OPTIMISATION FIRSTTEST.LOG

Vibrational frequencies of H₂

H₂ vibrations
Symmetry	SGG
Vibrational frequencies (cm⁻¹)	4466
IR intensities	0
Images

Charge distribution in H₂

Both atom represented on the image are hydrogen atoms. For the electronegatives of both hydrogens are equivalent, the atoms bear no charges, as expected.

The Haber–Bosch process

In the Haber–Bosch process, ammonia is produced from gaseous nitrogen and hydrogen.

E(NH₃)= -56.55777 a.u

2*E(NH₃)= -113.11554 a.u

E(N₂)= -109.52413 a.u

E(H₂)= -1.17854 a.u

3*E(H₂)= -3.53562 a.u

ΔE=2*E(NH₃)-[E(N₂)+3*E(H₂)]= -0.05579 a.u = -146.5 kJ/mol

The given reaction is strongly exothermic. Thus the product (ammonia) lies at a lower energy level than the starting materials and is more stable.

Molecule of choice: Hydrogen cyanide (HCN)

HCN information

HCN parameters
Parameter	Values
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
E(RB3LYP)	-93.42458132 a.u
RMS Gradient Norm	0.00017006 a.u
Point Group	C∞v
Optimised bond length (C-N)	1.16 Å
Optimised bond length (C-H)	1.07 Å
Optimised bond angle (H-C-N)	180°


Item	Value	Threshold	Converged?
Maximum Force	0.000370	0.000450	YES
RMS Force	0.000255	0.000300	YES
Maximum Displacement	0.000676	0.001800	YES
RMS Displacement	0.000427	0.001200	YES

Optimised NH3

Link to log file: File:SK7118 HCN FIRSTTEST.LOG

Vibrational frequencies of HCN

HCN vibrations
Symmetry	PI	PI	SG	SG
Vibrational frequencies (cm⁻¹)	767	767	2215	3480
IR intensities	35	35	2	57
Images

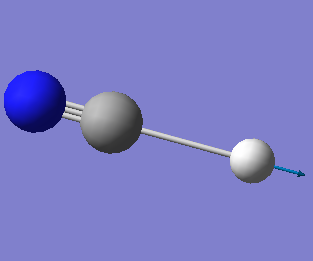
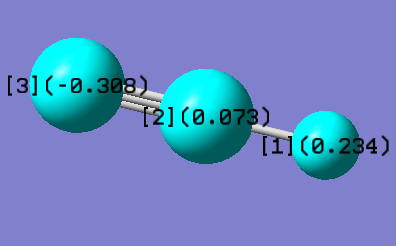
Charge distribution in HCN

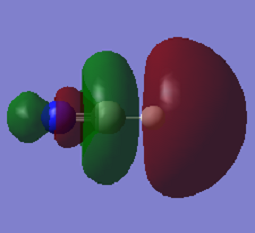
Atoms (1), (2) and (3) in the photo correspond to hydrogen, carbon and nitrogen, respectively. As nitrogen is more electronegative than carbon, it pulls electron density from C. Thus N obtains a negative charge. As C is more electronegative than H, it obtains a smaller positive charge than H but not a negative charge for it is also bonded to a nitrogen.

Molecular orbitals

Energies of first 10 MOs of HCN (eV)

**A selection of HCN molecular orbitals**
Number of MO	1	3	6	9	10
Images
Contributing AOs	Almost exclusively 1s on N, little from H 1s and C 1s and 2s	2s and 2pz on C and 2s and 3s on N. Little contribution from 1s on H.	2px and 3px for both C and N. No contribution from H.	2px and 3px on C. No contribution from N and H.	3p on C, main contribution from 2s on H. Very little contribution from N.
Energy	Low	Low	HOMO	LUMO	Near-LUMO
Character	Non-bonding	Questionable*	Bonding	Antibonding	Antibonding
Occupancy	Occupied	Occupied	Occupied	Unoccupied	Unoccupied
Effect on bonding	No effect (too low in energy).	Considerable effect on bonding.	Considerable effect on bonding. Electrons can be excited from this orbital to higher energy levels (LUMO, etc)	No effect on bonding since no electrons occupy the orbital at the ground state. On excitation, the LUMO is the lowest energy orbitals excited electrons can occupy.	No effect on bonding (too high in energy). Contains no electrons.

Note: * - this orbital is a canonical orbital and delocalized over the molecule and contributes to the C-N and C-H sigma bonds and the lone pair. Therefore it is hard to tell.

Extra: CO

CO information

CO parameters
Parameter	Value
Calculation Method	RB3LYP
Basis Set	6-31G(d,p)
E(RB3LYP)	-113.30945314 a.u
RMS Gradient Norm	0.00001828 a.u
Point Group	C∞v
Optimised bond length (C-O)	1.14 Å
Optimised bond angle (C-O)	180°

CO item table
Item	Value	Threshold	Converged?
Maximum Force	0.000032	0.000450	YES
RMS Force	0.000032	0.000300	YES
Maximum Displacement	0.000012	0.001800	YES
RMS Displacement	0.000018	0.001200	YES

Optimised CO

File:SK7118 CO FIRSTTEST.LOG

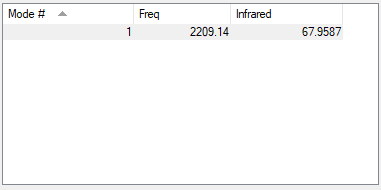
Vibrational frequencies of CO

CO vibrations
Symmetry	SG
Vibrational frequencies (cm⁻¹)	2209
IR intensities	68
Images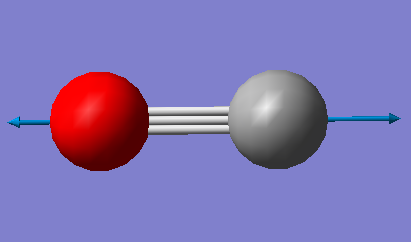

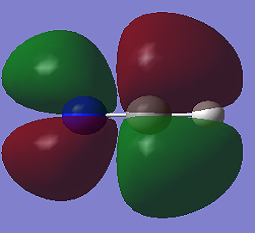
Charge distribution in CO

The green and red atoms in the photo correspond to carbon and oxygen, respectively. As oxygen is more electronegative than carbon, it withdraws electron density from carbon and thus obtains a negative charge. As the total charge of a neutral molecule must be 0, the charges are of equal magnitude but with opposite sign.

References

↑ ^1.0 ^1.1 T.Wagner, U.Englert, Structural Chemistry, 1997, 8, 357, DOI: 10.1007/BF02281249: https://www.ccdc.cam.ac.uk/structures/Search?Ccdcid=ZURKIG01&DatabaseToSearch=Published

Marking

Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.

Wiki structure and presentation 1/1

Is your wiki page clear and easy to follow, with consistent formatting?

YES

Do you effectively use tables, figures and subheadings to communicate your work?

YES - however the captions of your jmols are incorrect except for the last one. E.g. you labelled ammonia as NH and not NH3.

NH3 1/1

Have you completed the calculation and given a link to the file?

YES

Have you included summary and item tables in your wiki?

YES

Have you included a 3d jmol file or an image of the finished structure?

YES

Have you included the bond lengths and angles asked for?

YES

Have you included the “display vibrations” table?

YES

Have you added a table to your wiki listing the wavenumber and intensity of each vibration?

YES

Did you do the optional extra of adding images of the vibrations?

YES

Have you included answers to the questions about vibrations and charges in the lab script?

YES

N2 and H2 0/0.5

Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)

YES - However you stated bond angles for diatomic molecules. To define a bond angle three atoms are needed.

Crystal structure comparison 0.5/0.5

Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?

YES

Have you compared your optimised bond distance to the crystal structure bond distance?

YES

Haber-Bosch reaction energy calculation 1/1

Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]

YES

Have you reported your answers to the correct number of decimal places?

YES

Do your energies have the correct +/- sign?

YES

Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?

YES

Your choice of small molecule 3.5/5

Have you completed the calculation and included all relevant information?

YES

Have you added information about MOs and charges on atoms?

YES

You could have explained the calculated vibrations as you did for NH3. MO3 is definitely a bonding MO as it originates from s orbitals with the same phase only! MO9 is an out-of-phase combination of the 2px and 3px on C and N. If N would not contribute to this MO almost no electron density would be located close to it. You could have discussed the relative energies of the MOs in more detail.

Independence 1/1

If you have finished everything else and have spare time in the lab you could:

Check one of your results against the literature, or

Do an extra calculation on another small molecule, or