Rep:Mod:01492350
Molecular Modelling 2
NH3 (Ammonia)
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -56.55777 a.u. (atomic units)
RMS Gradient: 4.85 x 10-6 a.u. (atomic units)
Point Group: C3V
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
NH3 |
Bond Length (N-H):1.02 Å
Bond Angle (H-N-H):105.7°
The optimisation file is linked to here
| Wavenumber (cm-1) | 1089.5366 | 1693.9474 | 1693.9474 | 3461.2932 | 3589.8170 | 3589.8170 |
| Symmetry | A1 | E | E | A1 | E | E |
| Intensity (arbitrary units) | 145.3814 | 13.5533 | 13.5533 | 1.0608 | 0.2711 | 0.2711 |
| Image |  |
 |
|
 |
 |
|
Charges on atoms:
N=-1.125
H=0.375
One would expect the charge on the nitrogen to be more negative than the hydrogen(s) since nitrogen is more electronegative. Nitrogen therefore, withdraws electron density from the hydrogens making the hydrogens slightly positively charged (and making itself negatively charged).
Questions
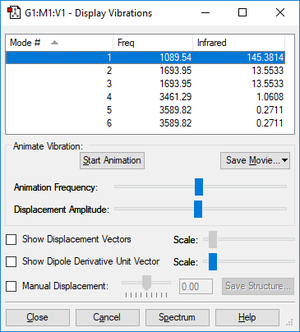
Using the 3N-6 rule, one would expect the NH3 molecule to have 6 vibrational modes (as value of N=4 for ammonia).
The 1693.95 cm-1 vibrational modes and 3589.82 cm-1 vibrational modes are degenerate; for each, there are two vibrational modes with that energy.
The 3461.29 cm-1 and 3589.82 cm-1 modes are bond stretching vibrations whereas the 1089.54 cm-1 and 1693.95 cm-1 modes are bending vibrations.
The vibrational mode with frequency 3461.29 cm-1 is highly symmetric.
The vibrational mode with frequency 1089.54 cm-1 is known as the 'umbrella mode'.
In an experimental spectrum of gaseous ammonia, there would be 2 bands observed. This is because, including degeneracy, there would be 4 signals. However, as the intensity is so low for 3589.82 cm-1 and 3461.29 cm-1 (around 0 and 1 respectively), these would not be observed.
H2 (Hydrogen)
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -1.17854 a.u. (atomic units)
RMS Gradient: 1.7 x 10-7 a.u. (atomic units)
Point Group: D∞H
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
H2 |
Bond Length (H-H):0.74 Å
The optimisation file is linked to here
| Wavenumber (cm-1) | 4465.6824 |
| Symmetry | SGG |
| Intensity (arbitrary units) | 0.0000 |
| Image |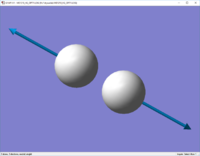 
|
Charges on atoms:
H=0.000
N2 (Nitrogen)
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -109.52413 a.u. (atomic units)
RMS Gradient: 6 x 10-7 a.u. (atomic units)
Point Group: D∞H
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
N2 |
Bond Length (N-N):1.11 Å
The optimisation file is linked to here
| Wavenumber (cm-1) | 2457.3283 |
| Symmetry | SGG |
| Intensity (arbitrary units) | 0.0000 |
| Image | 
|
Charges on atoms:
N=0.000
Nitrogen Orbitals - independence mark
The HOMO molecular orbital is the 3σg. This is made up of the 2pz atomic orbitals of each nitrogen atom. The LUMO molecular orbital is the 1π*g. This is made up of two 2px or two 2py atomic orbitals. It is an antibonding orbital.
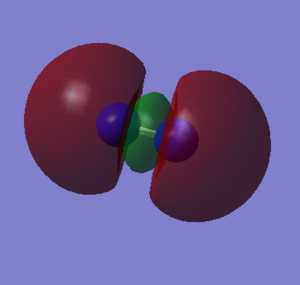
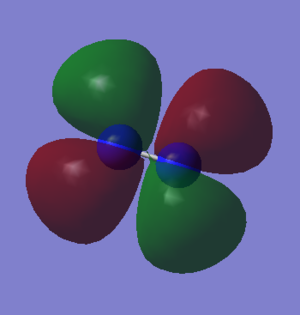
Nitrogen mono-metallic transition metal complex
Unique Identifier: BARTOF
Bond Length (N-N) in BARTOF complex:1.11218 Å
Bond Length (N-N) in optimised structure:1.10550 Å
BARTOF Complex |
https://www.ccdc.cam.ac.uk/structures/Search?Ccdcid=BARTOF&DatabaseToSearch=Published
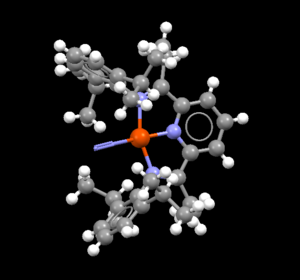
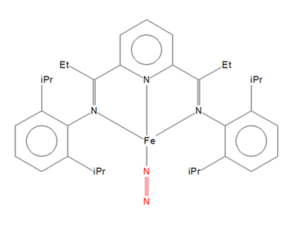
The bond distance in the computational model of N2 is lower than that found in the crystal structure of BARTOF. This is because the transition metal (Fe in this case) withdraws electron density from the nitrogen atom in the BARTOF complex. This weakens the bond between the nitrogen atoms so the bond distance is elongated. There may be errors in the computational calculations made which may mean the values differ (and do reflect those in real life).
Haber Process
E(NH3)=-56.55776873 a.u. 2*E(NH3)=-113.1155375 a.u. E(N2)=-109.52412868 a.u. E(H2)=-1.17853936 a.u. 3*E(H2)=-3.53561808 a.u. ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.05579 a.u. ΔE=-146.8 kJ mol-1 (energy to convert N2 (g) and H2 (g) into NH3 (g))
Therefore, as the value for ΔE is negative (exothermic), the NH3 is more stable.
HCN (Hydrogen Cyanide)
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -93.42458 a.u. (atomic units)
RMS Gradient: 1.7 x 10-4 a.u. (atomic units)
Point Group: C∞V
Item Value Threshold Converged?
Maximum Force 0.000370 0.000450 YES
RMS Force 0.000255 0.000300 YES
Maximum Displacement 0.000676 0.001800 YES
RMS Displacement 0.000427 0.001200 YES
HCN |
Bond Length (C-N):1.16 Å
Bond Length (C-H):1.07 Å
The optimisation file is linked to here
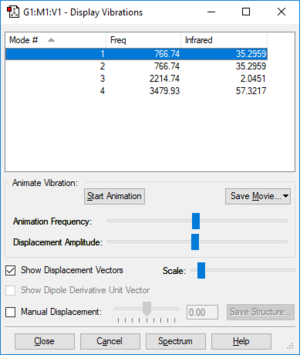
| Wavenumber (cm-1) | 766.7352 | 766.7352 | 2214.7397 | 3479.9336 |
| Symmetry | PI | PI | SG | SG |
| Intensity (arbitrary units) | 35.2959 | 35.2959 | 2.0451 | 57.3217 |
| Image |  |
 |
 |
|
The HCN molecule has four vibrational modes. Using the 3N-5 rule (for linear molecules), one would expect there to be 4 vibrational modes. There is one set of degenerate vibrational modes (with wavenumber 766.7352 cm-1.
The 2214.7397 cm-1 and 3479.9336 cm-1 modes are bond stretching vibrations whereas the 766.7352 cm-1 degenerate modes are bending vibrations.
In an experimental spectrum of 2 bands would be observed. This is because, including degeneracy, there would be 3 signals. However, as the intensity is so low for 2214.7397 cm-1 (only 2.0451), this would not be observed.
Charges on atoms:
C=0.073
N=-0.308
H=0.234
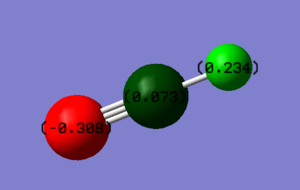
In the HCN molecule, the nitrogen (N) atom is the most electronegative. Therefore, the nitrogen atoms withdraws electron density from the carbon atom (C). Hence, the nitrogen has the most negative charge. Carbon is more electronegative than hydrogen so withdraws electron denisty from the hydrogen leading to a less positive charge on the carbon and a more positive charge on the hydrogen.
HCN Orbitals
| Molecular Orbital Type | 1π* (LUMO) antibonding | 1π (HOMO) bonding | 5σ bonding | 4σ* anti-bonding | 3σ bonding |
| Occupied with elctrons? | No | Yes | Yes | Yes | Yes |
| Atomic Orbitals | The 3px/y and 2px/y from N and those from C contribute significantly | The 2px/y from the N, 2px/y from the C contribute significantly | 2pz from N and from C contribute significantly along with the 2s orbital of H | The 2s and 3s from the N, 2pz from C and 1s from H contribute significantly | The 2s and 3s from the N contribute singificantly along with the 2s from the C |
| Energy (a.u.) | 0.01929 | -0.35939 | -0.38064 | -0.60777 | -0.91995 |
| Image |  |
 |
 |
 |
|
The LOG file was used to evaluate the atomic orbital contributions to each molecular orbital in the HCN molecule. The % contribution from each AO is listed in the LOG file. The atomic orbitals that make up molecular orbitals are not so definitive and clear-cut. Instead, some atomic orbital will contribute a small percentage towards the MO. For example, in the 4σ* anti-bonding molecular orbital, there is a 15% contribution from 2s (N) and 15% contribution from 3s (N). Therefore, it cannot be said that the nitrogen only gives the 2s towards this molecular orbital.
There are degenerate orbitals (with the same energy). These are the 1π* and 1π. The 1π* and 1π orbitals are made up of px or py atomic orbitals. These have the same energy. The overlap between px orbitals or py orbitals is equivalent and forms a π bond with electron denisty above/ below the plane of the molecule. The overlap between pz orbitals, however, is greater and forms along the plane. This forms a σ bond.
There are 2π bonds and a σ bond between the carbon and the nitrogen atoms. There is only a σ bond between the hydrogen and the carbon. Other orbitals like 1σ and 2σ* are deep in energy (with energies of -14.36 a.u. and -10.25 a.u. respectively) so won't have an effect on bonding. Therefore, they do not need to be considered.
CO (Carbon monoxide) - independence mark
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy E(RB3LYP): -113.30945 a.u. (atomic units)
RMS Gradient: 1.83 x 10-5 a.u. (atomic units)
Point Group: C∞V
Item Value Threshold Converged?
Maximum Force 0.000032 0.000450 YES
RMS Force 0.000032 0.000300 YES
Maximum Displacement 0.000012 0.001800 YES
RMS Displacement 0.000018 0.001200 YES
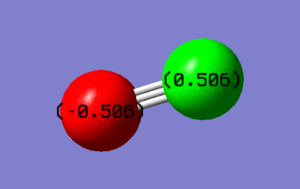
CO |
Bond Length (C-O):1.14 Å
The optimisation file is linked to here
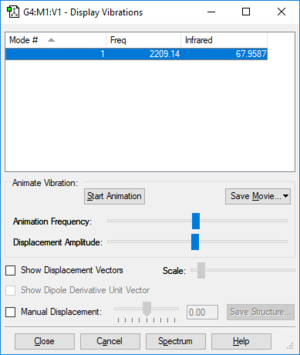
| Wavenumber (cm-1) | 2209.1389 |
| Symmetry | SG |
| Intensity (arbitrary units) | 67.9587 |
| Image | 
|
Charges on atoms:
C=0.506
O=-0.506
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4.5/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES, you have looked into the MOs especially with a lot of detail, well done. The one point I would disagree with is that if the 4 sigma star MO has contributions from the C 2pz then the node is at the C atom and not between the atoms so there are bonding interactions between the C and N and the C and H atoms, not antibonding.
Independence 1/1
If you have finished everything else and have spare time in the lab you could:
Check one of your results against the literature, or
Do an extra calculation on another small molecule, or
Do some deeper analysis on your results so far
You looked at the N2 MOs and calculated CO independently, well done!