Rep:Mod:01390203
Ammonia (NH3)
Method of optimisation
- Calculation method: RB3LYP
- Calculation type: FREQ
- Basis set: 6-31G(d,p)
- Energy in a.u (atomic units): -56.55776873
- RMS Gradient in a.u: 0.00000485
- Point group: C3v/
Item summaries
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000004 | 0.000450 | Yes |
| RMS Force | 0.000004 | 0.000300 | Yes |
| Maximum Displacement | 0.000072 | 0.001800 | Yes |
| RMS displacement | 0.000035 | 0.001200 | Yes |
Bond measurements and molecular geometry
N-H: 1.01798 Angstrom
H-N-H Bond angle: 105.741 degrees
NH3 has a central Nitrogen atom and is surrounded by three hydrogen atoms. The Nitrogen also has a lone pair and therefore has a tetrahedral pseudostructure. However, due to the presence of the lone pair and the extra repulsion experienced due to this lone pair, the actual structure is trigonal pyramidal. It is for this reason why the bond angles are not 120 degrees. This structure can be visualised below:
test molecule |
File:ANDREW ANDREAS PHUNT NH3 OPTF POP.LOG
Vibrational analysis
Six vibrational modes were observed:
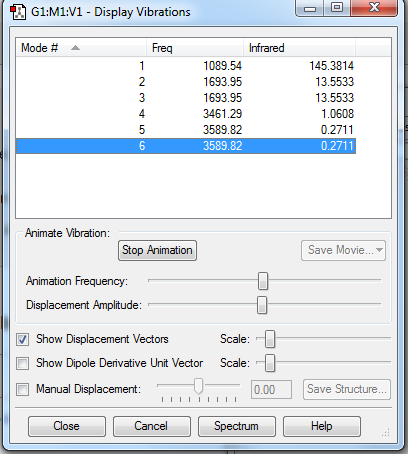
- Theory would suggest that there would be 3N-6 vibrational modes as NH3 is non-linear. This would translate to 6 vibrational modes which were observed through calculation.
- Modes 2 and 3, and modes 5 and 6 are degenerate
- 1,2 and 3 are bending whilst 4,5 and 6 are stretching modes
- 1 is a symmetric bend and 4 is a symmetric stretch
- 1 is an umbrella mode
- Two bands could be expected via spectral analysis as they have sufficient energy whilst the other low energy bands would not be observed.
A visual aid to picture the symmetric stretch observed in NH3 can be seen below:
Atomic charge
Calculation of atomic charge of NH3 yielded:

This correlates well with theory - Nitrogen is more electronegative than Hydrogen and so it's atomic orbitals are lower in energy. As such, upon forming the bonding molecular orbitals, the electrons lie closer towards the Nitrogen and hence result in a lower atomic charge.
Nitrogen (N2)
Method of optimisation
- Calculation method: RB3LYP
- Calculation type: FREQ
- Basis set: 6-31G(d,p)
- Energy in a.u (atomic units): -109.52412868
- RMS Gradient in a.u: 0.00000365
- Point group: D*H
Item summaries
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000006 | 0.000450 | Yes |
| RMS Force | 0.000006 | 0.000300 | Yes |
| Maximum Displacement | 0.000002 | 0.001800 | Yes |
| RMS displacement | 0.000003 | 0.001200 | Yes |
Bond measurements and molecular geometry
Bond length: 1.0550 Angstrom
Bond angle: 180 degrees
N2 is a diatomic molecule with a linear structure, in which each Nitrogen atom is triple bonded to the other Nitrogen atom.
N2 can be visualised below:
test molecule |
Vibrational analysis
Vibrational analysis of N2 yielded:
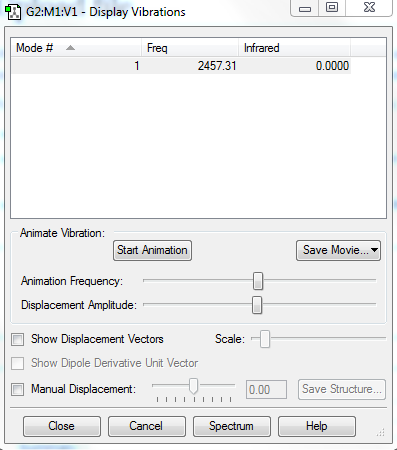
An illustration of this stretch can be seen below:
Atomic charge
Calculation of atomic charge of N2 yielded:
As N2 is a homonuclear diatomic it experiences no atomic charge as both molecular orbitals are identical and they share electron density equally due to their equal energy atomic orbitals.
Hydrogen (H2)
Method of optimisation
- Calculation method: RB3LYP
- Calculation type: FREQ
- Basis set: 6-31G(d,p)
- Energy in a.u (atomic units): -1.17853930
- RMS Gradient in a.u: 0.0000012170
- Point group: D*H
Item summaries
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000211 | 0.000450 | Yes |
| RMS Force | 0.000211 | 0.000300 | Yes |
| Maximum Displacement | 0.000278 | 0.001800 | Yes |
| RMS displacement | 0.000393 | 0.001200 | Yes |
Bond measurements and molecular geometry
Bond length: 0.74309
Bond angle: 180
H2 is a diatomic, compromised of two Hydrogen atoms singularly bonded to one another. It's pseudostructure and structure and both linear and the 180 degree bond angle is expected.
H2 can be visualised below:
test molecule |
Vibrational analysis
Vibrational analysis of yielded:
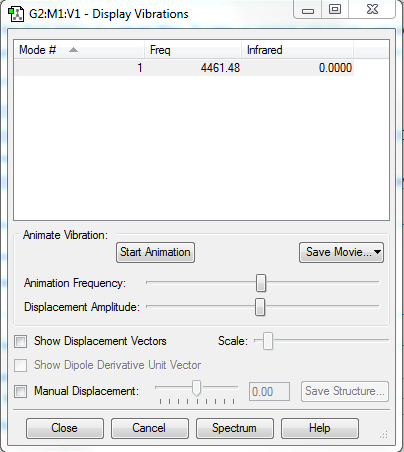
An illustration of this stretch can be seen below:
Atomic charge
Calculation of H2 atomic charge yielded:

As H2 is a homonuclear diatomic atomic charge is zero because the atomic orbitals are of the same energy and contribute equally to the molecular orbitals.
Energetics for the production of Ammonia
Ammonia can be produced by reaction one mol of N2 alongside three moles of H2 to produce two moles of NH3. This reaction is known commercially as the Haber Process and is used to produce Ammonia on an industrial scale. Calculations for the production of Ammonia for the reaction is calculated below in atomic units (a.u)
| Calculation | E/a.u |
|---|---|
| E(NH3) | -56.55776873 |
| 2*E(NH3) | -113.1155375 |
| E(N2) | -109.5241287 |
| E(H2) | -1.1785393 |
| 3*E(H2) | -3.5356179 |
| ΔE=2*E(NH3)-[E(N2)+3*E(H2)] | -0.05579088 |
The overall energy change for the reaction of N2 gas and H2 gas to produce NH3/) is -146.82 KJ for 2 moles of NH3. Therefore, the overall energy change for the reaction in the production of Ammonia from gaseous Nitrogen and Hydrogen is -73.41 KJ/mol. This indicates that the product, Ammonia, is more stable than its reactant gases as the overall enthalpy change is negative.
Fluorine (F2)
Method of optimisation
- Calculation method: RB3LYP
- Calculation type: FREQ
- Basis set: 6-31G(d,p)
- Energy in a.u (atomic units): -199.49825218
- RMS Gradient in a.u: 0.00007365
- Point group: D*H
Item summaries
| Item | Value | Threshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000128 | 0.000450 | Yes |
| RMS Force | 0.000128 | 0.000300 | Yes |
| Maximum Displacement | 0.000156 | 0.001800 | Yes |
| RMS displacement | 0.000221 | 0.001200 | Yes |
Bond measurements and molecular geometry
Bond length: 1.40281
Bond angle : 180
F2 is a diatomic molecule that is formed when two fluorine atoms bind singularly to one another. It therefore has a linear geometry and it's 180 degree bond angle is expected.
F2 can be visualised below:
test molecule |
Vibrational analysis
Vibrational analysis of F2 yielded:
F2 has a symmetric stretch
Atomic Charge
Atomic charge on each atom is zero because F2 is a homonuclear diatomic and the atomic orbitals are of the same energy and contribute equally to the molecular orbitals.

Molecular Orbitals
The following are the Molecular Orbitals which I selected of interest.
1 sigma g

This MO is a product of the constructive overlap between the two 1s orbitals on each Fluorine atom to produce a bonding orbital. Each 1s orbital contributes 1 electron to this bonding orbital. This orbital is very deep in energy and is not involved in bonding.
1 Pi u

This is the Pi bonding MO containing 2 electrons, in which the orthogonal 2Px (chosen arbitarily as it can be 2Py) atomic orbitals on the first Fluorine atom overlap with the corresponding 2Px orbital on the other Fluorine atom. Electron density is centred above and below the inter nuclear axis and so there is less overlap between the p orbitals in comparison to the head-on overlap observed in sigma bonds. They are therefore less strongly bonded than sigma bonding orbitals. The Pi MO is not deep in energy.
1 Pi g*

This is the Pi anti-bonding MO containing 2 electrons, in which the orthogonal 2Px and 2Py atomic orbitals on the first Fluorine atom overlap out of phase with the corresponding 2Px and 2Py atomic orbitals on the other Fluorine atom. The Pi* MO is also the HOMO of the molecule which enable it to act as a nucleophile; this is the orbital in which Fluorine will donate its lone pair of electrons from.
3 sigma* u =

This is the sigma anti-bonding MO that is unoccupied. It is made from the out of phase head-on overlap of the 2Pz orbitals (The 2Pz orbital is chosen here arbitrarily as it can be either of the three P orbitals). This is also the LUMO; however F2 cannot accept a lone pair of electrons as its bond order would become zero. The bond order is given by [Electrons in bonding orbitals] - [Electrons in anti-bonding orbitals].
1 sigma* u
This is the 1s sigma anti-bonding orbital which is occupied and deep in energy. As it is deep in energy it does not contribute to the bonding. It is formed by the head on out-of-phase overlap of the 1s orbitals on each Fluorine.
