Rep:Mod:01381641
Optimisation of an NH3 Molecule
Summary
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy, E:-56.55776873
Point Group: C3v
RMS gradient: 0.00000485
Optimisation Output
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
File:SHAZEEN PHUNT NH3 OPTF POP.LOG
Ammonia |
N-H Bond Length - 1.01798 au
H-N-H Bond Angle - 105.7o
From the valence shell electron repulsion theory, a bond angle of around 107o would be expected so the angle of 105.7 is a good output after optimisation as it is close.
Ensuring optimisation has completed correctly
No negative frequencies present so optimisation completed correctly.
Analysis
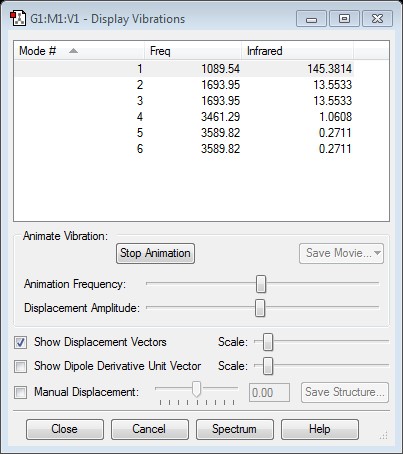
Modes expected from the 3N-6 rule: 6
Degenerate Modes: 2 & 3, 5 & 6
'Bending' Vibrations Modes: 1, 2, 3
'Stretching' Vibrations Modes: 4, 5, 6
Highly Symmetric Mode: 4
'Umbrella' Mode: 1
Symmetric Stretch: 4
There would be 2 bands expected in an experimental spectrum of gaseous ammonia which would be for modes 1 & 2/3. Modes 2 and 3 are degenerate so would have the same band. The rest of the modes would not be seen as the intensity is too low. This is because the vibrations do not cause a change in dipole moment hence are not infrared active.
Charge on N-atom: -1.125 Charge on H-atom: 0.375
As nitrogen is more electronegative than hydrogen, it would draw most of the electron density towards itself giving itself a negative charge compared to hydrogen which would have a positive charge.
Optimisation of an N2
Summary
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Total Energy: -109.52412868 a.u.
RMS Gradient: 0.00000060 a.u.
Point Group: D∞h
Optimisation Output
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
N2 |
File:SHAZEEN N2 CALCULATION.LOG
Ensuring optimisation completed correctly
No negative frequencies present therefore optimisation completed successfully
Optimisation of a H2
Summary
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Total Energy, E: -1.17853936 a.u.
RMS Gradient: 0.00000017 a.u.
Point Group: D∞h
Optimisation Output
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
File:SHAZEEN H2 CALCULATION.LOG
H2 |
No negative frequencies suggest optimisation completed correctly.
Evaluating The Haber-Bosch Process
A Hess Cycle can be used to calculate the enthalpy of the reaction:
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u.
ΔE in KJ/mol: -146.47849401
The negative value for ΔE suggests the reaction is exothermic, therefore releasing energy. This means that NH3 is more stable than nitrogen and hydrogen as it has less energy.
Optimisation of a F2 Molecule
Summary
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Total Energy, E: -199.42620785
RMS Gradient: 0.23253407
Point Group: D∞h
Optimisation Output
Item Value Threshold Converged? Maximum Force 0.000128 0.000450 YES RMS Force 0.000128 0.000300 YES Maximum Displacement 0.000156 0.001800 YES RMS Displacement 0.000221 0.001200 YES
F2 |
No negative frequencies can be seen suggesting optimisation has completed correctly.
Charges on individual F atoms: 0
F2 is expected to be neutral molecule with no dipole as the individual atoms are the same so the electron density is shared equally.
Molecular Orbitals
The electronic configuration of a nitrogen atom is 1s22s22p5. When the fluorine atoms combine to from F2, the atomic orbitals (AOs) combine to form molecular orbitals (MOs).
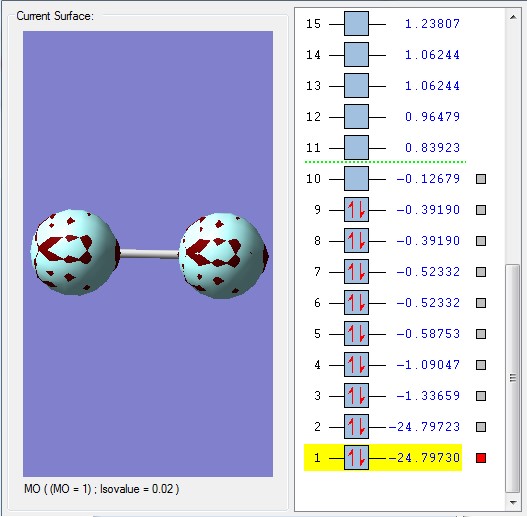
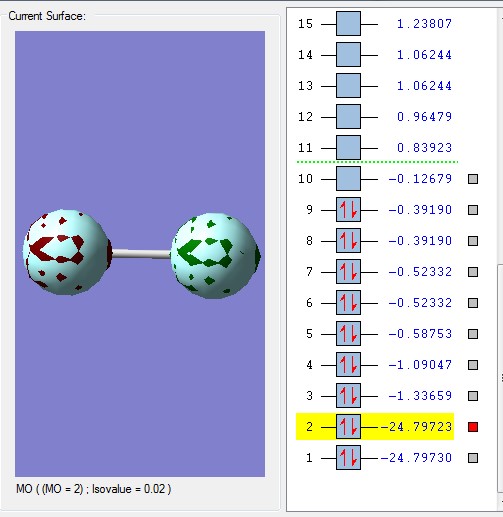
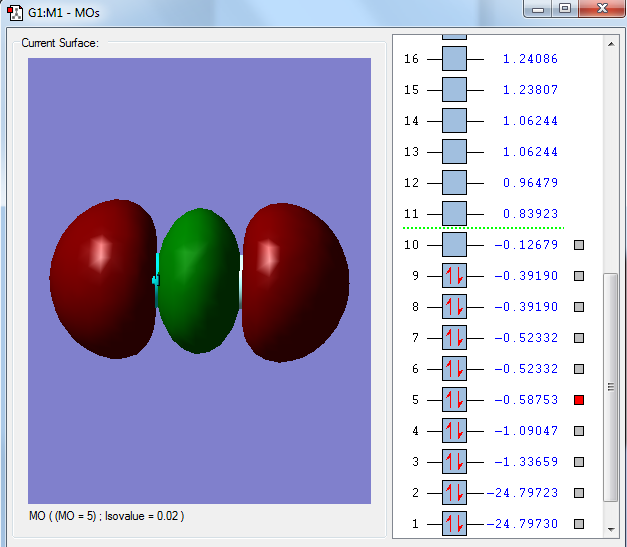
The core 1s atomic orbitals are so far apart in energy that they do not overlap so become non-bonding orbitals being held tightly to their respective nuclei and are not involved in chemical bonding. They are very deep in energy, -24.797 au which is much deeper than the molecular orbitals formed from the valence shell atomic orbitals shown below.
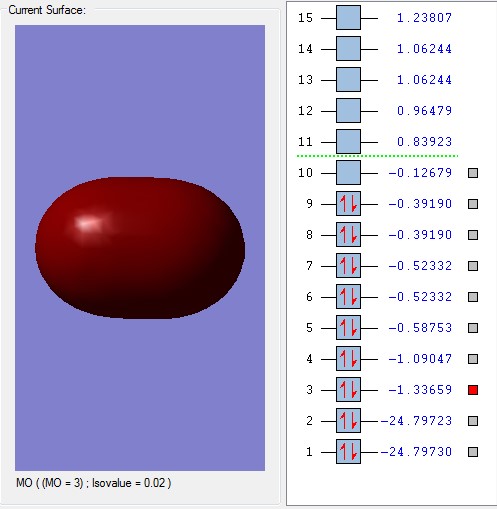
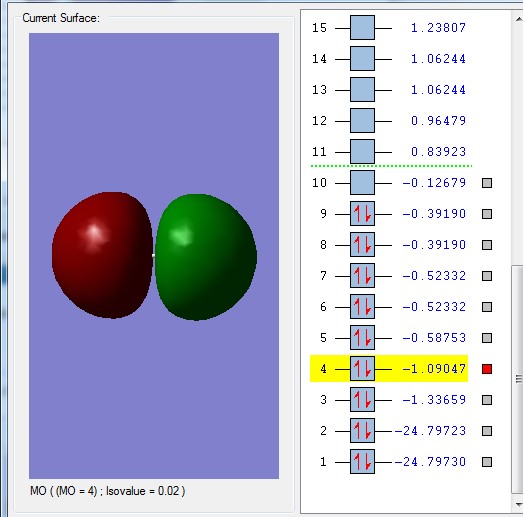
Molecular Orbital 3 is the bonding combination of the 2s atomic orbitals and 4 is the antibonding combination. The overlap is stronger with a greater energy. The bonding overlap is really strong which is why one extensive surface is seen. There is also a greater difference between the bonding and antibonding orbitals due to the better overlap.
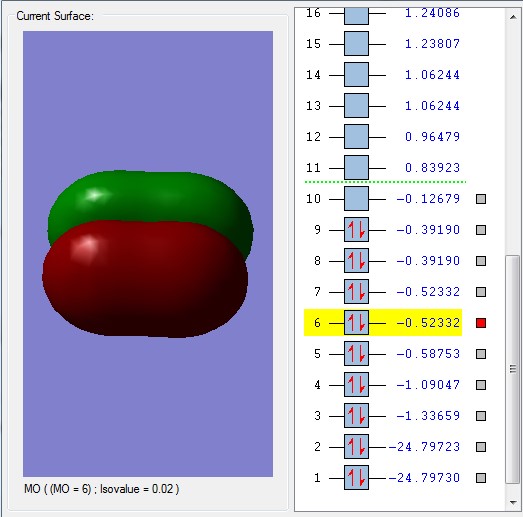
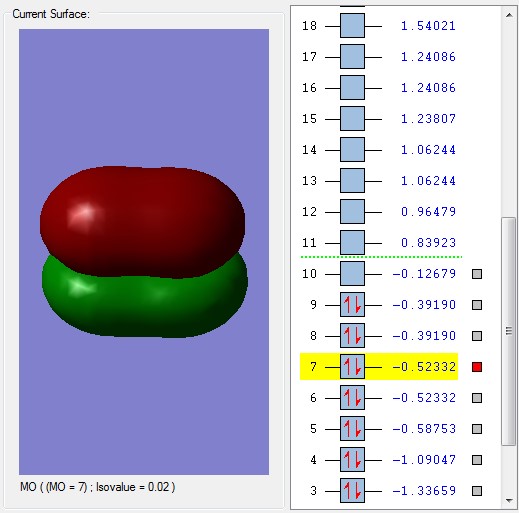
The bonding molecular orbital 5 is formed from the overlap of the 2p orbitals in the plane of the bond, forming the sigma bond. MOs 6 and 7 are also bonding combinations of the two 2p orbitals but in the orthogonal directions and are degenerate (have the same energy).