Rep:Mod:01366863

Intro to Molecule Modelling 2

Below, two molecules(NH3 and F2) will be analysed using GaussView.

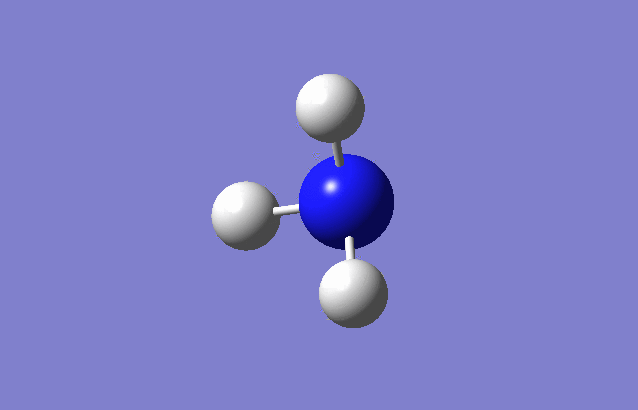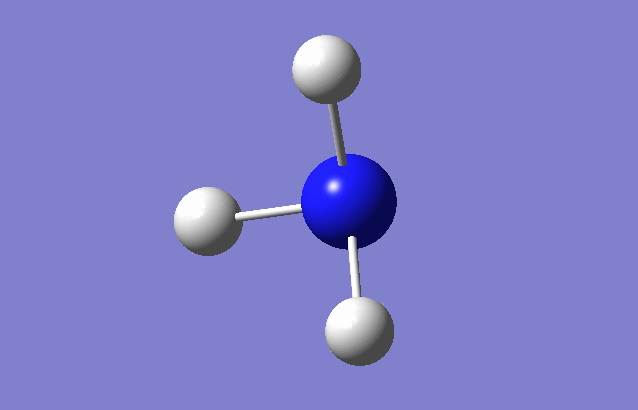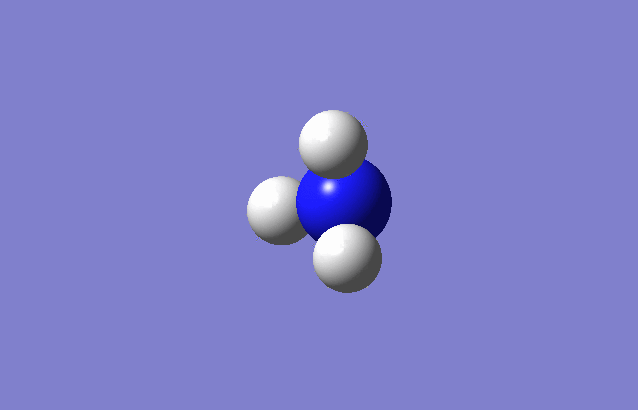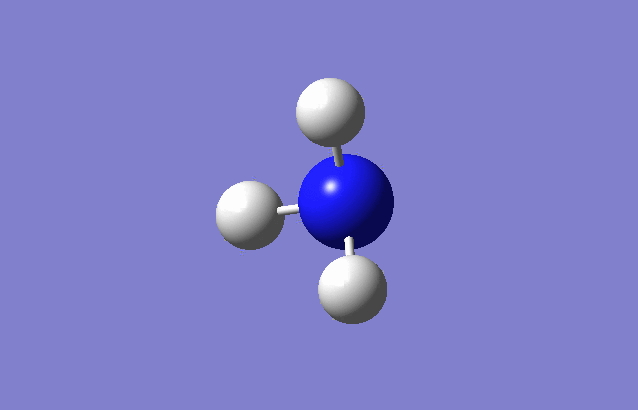
Analyzed Molecule:NH3

Summary

Molecule name = NH3(ammonia)

Calculation method = RB3LYP

Basis set = 6-31G(d,p)

Final energy = -56.44397188 a.u.

Point Group = C3V

Dipole Moment = 1.5008 Debye

Bond Length = 1.3 angstrom

Bond Angle(H-N-H) = 105.74 degree

Spin = Singlet

 Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.986292D-10
 Optimization completed.
    -- Stationary point found.

The *.log file of NH3:File:NH3 OPTF.LOG

Vibrations

NH3 has 6 vibration modes.

- According to the table, the second and the third mode, also the fifth and the sixth mode are degenerate since they have the same frequency hence energy.

- Running the GaussView and animating the vibration function, it is clearly shown that Mode1,2&3 are "bending" vibrations and Mode4,5&6 are "stretching" vibrations.

- The highly vibrating mode is mode 4. N-H bonds are stretching along with their own direction and the dipole moment can cancel out in this case.

Mode4

- The "umbrella" mode is mode 1, since the three N-H bonds are bending towards the same direction like an umbrella lid does.

Mode1

- Four bands are expected to be seen in the spectrum because despite the degenerate modes, there are four modes with different energies.

Atomic Charges

q(N)= -1.132

q(H)= 0.377

The molecule NH3 is generally neutral.

Reaction Energies

E(NH3)= -56.56 a.u.

2*E(NH3)= -113.12 a.u.

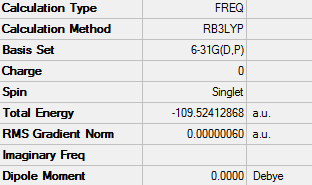
E(N2)= -109.52 a.u.

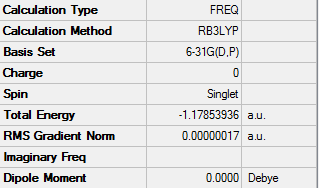
E(H2)= -1.16 a.u.

3*E(H2)= -3.48 a.u.

ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.12 a.u.

ΔE= -0.12*2625.5 = -315.06 kJ/mol

The energy for converting hydrogen and nitrogen gas into ammonia gas is -315.06 kJ/mol. It can be seen that the energy difference of the reaction is a negative value, which indicates that Haber-Bosch Process is exothermic and releases energy. Since less energy equals more stable, the gaseous product is more stable than the gaseous reactants.

Calculation of N2

The *.log file of N2:File:N2 OPTF.LOG

Calculation of H2

The *.log file of H2:File:H2 OPTF.LOG

Small Molecule:F2

Summary

Molecule name = F2(fluorine)

Calculation method = RB3LYP

Basis set = 6-31G(d,p)

Final energy = -199.42620785 a.u.

Point Group = D*H

Dipole Moment = 0.0000 Debye

Bond Length = 1.403 angstrom

Bond Angle = 180 degree

         Item               Value     Threshold  Converged?
 Maximum Force            0.000128     0.000450     YES
 RMS     Force            0.000128     0.000300     YES
 Maximum Displacement     0.000156     0.001800     YES
 RMS     Displacement     0.000221     0.001200     YES
 Predicted change in Energy=-1.995024D-08
 Optimization completed.
    -- Stationary point found.

The .*log file of F2: File:F2 OPTF.LOG

Vibrations

-Only one vibration mode is expected because F2 is a linear molecule.

-The vibration mode is a "stretching" mode.

-It is highly symmetric and the dipole moment cancels out completely.

Atomic Charges

q(F)= 0.000

This diatomic molecule is symmetric and its atoms are identical, hence it gives the atomic charges of zero.

Reaction Energies

For the formation of HF:

E(F2)= -199.43 a.u.

E(H2)= -1.16 a.u.

E(HF)= -100.42 a.u.

2*E(HF)= -200.84 a.u.

ΔE=2*E(HF)-[E(H2)+E(F2)]= -0.25 a.u.

ΔE= -0.25*2625.5 = -656.38 kJ/mol

Molecular Orbitals

1.MO = 3

This MO is combined from two 2s AOs of F, and it is a σg bonding MO. It's quite deep in energy and it sure is occupied.

2.MO = 4

This MO is also combined from two 2s AOs of F, and it is a σ*u anti-bonding MO. It's also deep in energy but slightly higher than MO=3, and it is occupied.

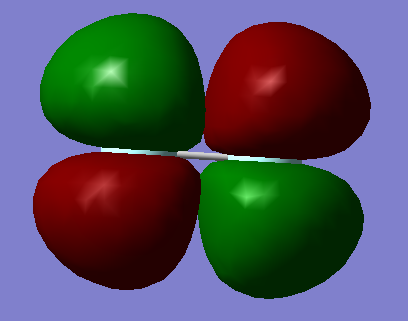
3.MO = 6

This MO is combined from two 2P AOs of F, and it is a πu bonding MO. It's deeper in energy than the HOMO and higher than the previous two, also it is occupied.

4.MO = 8

This MO is combined from two 2p AOs of F, and it is a π*g anti-bonding MO. This MO is π*g which means it's in HOMO region in this case and it is still occupied.

5.1.MO = 10

This MO is combined from two 2p AOs of F, and it is a σ*u bonding MO. It's right in the LUMO region (higher than all the MOs mentioned previously) and it is unoccupied since the occupied MOs are up to MO = 9.