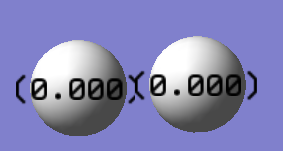Rep:Mod:01365318,XYK17
NH3
Molecule: NH3
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -56.55776873 au
RMS gradient: 0.00000485 au
Point group: C3V
Optimised N-H bond distance: 1.01798 Angstrom
Optimised H-N-H bond angle: 105.741o
NH3 |
| Item | Value | Treshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000004 | 0.000450 | YES |
| RMS Force | 0.000004 | 0.000300 | YES |
| Maximum Displacement | 0.000070 | 0.001800 | YES |
| RMS Displacement | 0.000033 | 0.001200 | YES |
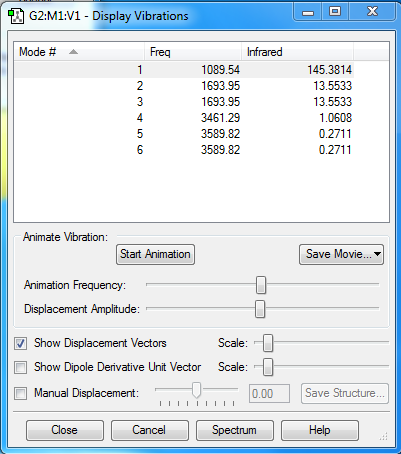
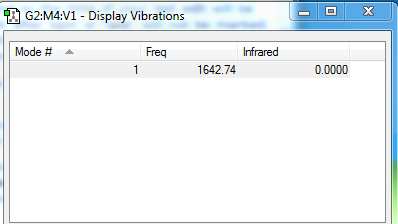
Vibrations
Expected number of vibrational modes: [3(4)-6]= 6
Degenerate modes: mode 2 and mode 3, mode 5 and mode 6
"Bending" vibrations: mode 1, mode 2 and mode 3
"Stretching" vibrations: mode 4, mode 5 and mode 6
Symmetric mode: mode 4, mode 5 and mode 6
Umbrella mode: mode 1
Expected number of bands observed an experimental spectrum: 2
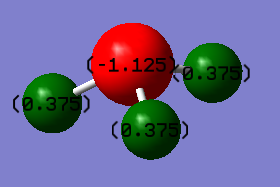
Charge distribution
Charge on the N-atom: -1.125
charge on the H-atom: 0.375
These values agree with the theory, as N is more electronegative than H, therefore it tends to attract the shared pair of electrons more strongly towards itself, resulting in greater electron charge cloud which develops negative charge.
Media:01365318_XYK17_NH3_OPTF_POP.LOG
H2
Molecule: H2
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -1.17853929 au
RMS gradient: 0.00013424 au
Point group: D*H
Optimised H-H bond distance: 0.74247 Angstrom
Optimised H-H bond angle: 180o
H2 |
| Item | Value | Treshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000232 | 0.000450 | YES |
| RMS Force | 0.000232 | 0.000300 | YES |
| Maximum Displacement | 0.000305 | 0.001800 | YES |
| RMS Displacement | 0.000431 | 0.001200 | YES |
Vibrations
There is only one frequency, which is responsible for the "stretching" vibration of H-H bond - the stretching frequency. There's only one vibrational mode, according to [3(2)-5] = 1. It is a symmetric mode. In order for a molecule to absorb IR, its vibration must cause a net change in dipole moment of the molecule. Since the only mode is a symmetric stretch, and there's no change in dipole moment, therefore no band/peak will be observed in the IR spectrum.
Charge distribution
The charges on both H atoms are zero.
This is because both atoms in the molecule are the same, therefore there's zero electronegativity difference.
Media:01365318_XYK17_1H2_OPTF_POP.LOG
N2
Molecule: N2
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -109.52412868 au
RMS gradient: 0.00000060 au
Point group: D*H
Optimised NΞN bond distance: 1.10550 Angstrom
Optimised NΞN bond angle: 180o
N2 |
| Item | Value | Treshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000001 | 0.000450 | YES |
| RMS Force | 0.000001 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000000 | 0.001200 | YES |
Vibrations
There is only one frequency, which is responsible for the "stretching" vibration of nitrogen bond - the stretching frequency. There's only one vibrational mode, according to [3(2)-5] = 1. It is a symmetric mode. In order for a molecule to absorb IR, its vibration must cause a net change in dipole moment of the molecule. Since the only mode is a symmetric stretch and there's no change in dipole moment, therefore no band/peak will be observed in the IR spectrum.
Charge distribution
The charges on both N atoms are zero.
This is because both atoms in the molecule are the same, therefore there's zero electronegativity difference.
Media:01365318_XYK17_2N2_OPTF_POP.LOG
Reaction energies for Haber Process
E(NH3)= -56.55776873 au
2*E(NH3)= -113.1155375 au
E(N2)= -109.52412868 au
E(H2)= -1.17853929 au
3*E(H2)= -3.53561787 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579103 au
= -146.48 kJ/mol (2 dp)
The energy difference is negative. This reaction is exothermic, and heat is released. Therefore the ammonia product is more stable than the gaseous reactants.
Literature value for energy change= -92.4 kJ/mol [1]
The difference in energy change with the experimental value might be due to the different solvent as well as the conditions of the reaction process.
A molecule of my choice: O2
Molecule: O2
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: -150.25742434 au
RMS gradient: 0.00007502 au
Point group: D*H
Optimised O=O bond distance: 1.21602 Angstrom
Optimised O=O bond angle: 180o
O2 |
| Item | Value | Treshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000001 | 0.000450 | YES |
| RMS Force | 0.000001 | 0.000300 | YES |
| Maximum Displacement | 0.000000 | 0.001800 | YES |
| RMS Displacement | 0.000000 | 0.001200 | YES |
Vibrations
There is only one frequency, which is responsible for the "stretching" vibration of O=O bond - the stretching frequency. There's only one vibrational mode, according to [3(2)-5] = 1. It is a symmetric mode. In order for a molecule to absorb IR, its vibration must cause a net change in dipole moment of the molecule. Since the only mode is a symmetric stretch and there's no change in dipole moment, therefore no band/peak will be observed in the IR spectrum.
Charge distribution
The charges on both O atoms are zero.
This is because both atoms in the molecule are the same, therefore there's zero electronegativity difference.
Molecular orbitals
MO 1 (1st MO)
This molecular orbital(MO) which has the lowest energy, is a combination of the two 1s atomic orbitals(AOs) of each O atom.
It is a bonding orbital.
It is very deep in energy - -19.30736 au, which is -19.13 au much deeper than the MOs formed from the valence shell AOs. This is due to the fact that 1s atomic orbitals are smallest in size and are held very tightly to the nuclei.
It is occupied with 2 electrons.
Since the 1s AOs hardly overlap, the MO is not involved in bonding.
MO 2 (4th MO)
This MO is the combination of the 2s valence AOs.
It is an antibonding orbital.
Its energy which is -0.79821 au is much higher than the first 2 MOs.
It is occupied with 2 electrons.
The AOs overlap more strongly and effectively, and since they are valence orbitals they are much more involved in chemical bonding.
MO 3 (5th MO)
This MO is the combination of the 2p AOs. It is formed by sigma bond, which is the end-on overlap of the two p AOs along the bond.
It is a bonding orbital.
Its energy is considerably high - -0.53151 au.
It is occupied with 2 electrons.
The AOs overlap strongly and effectively, and since they are valence orbitals they have huge contribution to chemical bonding.
MO 4 (8th MO)
This MO is the combination of the 2p AOs. It is formed by pi bond, which is the side-by-side overlap of the two p AOs perpendicular the bond.
It is degenerate with another MO (which is the 9th MO, stated below).
It is an antibonding orbital.
It is the HOMO.
It is occupied.
It has huge contribution to the chemical bonding.
MO 5 (9th MO)
This MO is the combination of the 2p AOs. It is formed by pi bond, which is the side-by-side overlap of the two p AOs perpendicular the bond.
It is degenerate with another MO (which is the 8th MO, stated above).
It is an antibonding orbital.
It is the LUMO.
It is unoccupied.
Media:01365318_XYK17_O2_OPTF_POP.LOG
Independence - Second molecule of my choice: HCl
Molecule: HCl
Calculation method: RB3LYP
Basis set: 6-31G(d.p)
Final energy: --460.80077875 au
RMS gradient: 0.00005211 au
Point group: C*V
Optimised H-Cl bond distance: 1.28599 Angstrom
Optimised H-Cl bond angle: 180o
HCl |
| Item | Value | Treshold | Converged? |
|---|---|---|---|
| Maximum Force | 0.000090 | 0.000450 | YES |
| RMS Force | 0.000090 | 0.000300 | YES |
| Maximum Displacement | 0.000139 | 0.001800 | YES |
| RMS Displacement | 0.000197 | 0.001200 | YES |
Vibrations
There is only one frequency, which is responsible for the "stretching" vibration of H-Cl bond - the stretching frequency. There's only one vibrational mode, according to [3(2)-5] = 1. It is an asymmetric mode, due to the difference in electronegativities between H and Cl. In order for a molecule to absorb IR, its vibration must cause a net change in dipole moment of the molecule. Since the the mode is a asymmetric stretch and there's net change in dipole moment, therefore one band/peak will be observed in the IR spectrum.
Charge distribution
Charge on the Cl-atom: -0.284
Charge on the H-atom: 0.284
These values agree with the theory, as Cl is more electronegative than H, therefore it tends to attract the shared pair of electrons more strongly towards itself, resulting in greater electron charge cloud which develops negative charge.
Media:01365318_XYK17_HCL_OPTF_POP.LOG
References
- ↑ AUS-e-TUTE, 14 February 2017 "Haber Process for Ammonia Production Chemistry Tutorial" Available from http://www.ausetute.com.au/haberpro.html