Rep:Mod:01364124
NH3 Molecule
N-H Bond Length: 1.018 Angstrom
H-N-H Bond Angle: 105.745 Degrees
Optimisation
Molecule: Ammonia
Calculation: Method: RB3LYP
Basis Set: 6-31G(D.P)
Final Energy: -56.55776873 a.u.
RMS Gradient: 0.00000323
Point Group: C2V
Ammonia |
click here for link to fully optimised NH3
Item-Table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000009 0.001200 YES
As shown by the item table, the structure has converged.
Frequency-Analysis
| Mode | Frequency | Infrared |
|---|---|---|
| 1 | 1089.54 | 145.3814 |
| 2 | 1693.95 | 13.5533 |
| 3 | 1693.95 | 13.5533 |
| 4 | 3461.29 | 1.0608 |
| 5 | 3589.82 | 0.2711 |
| 6 | 3589.82 | 0.2711 |
There is no negative frequencies which indicates that the molecule has been fully optimised.
According to the 3N-6 rule, six vibrational modes are expected for ammonia. As seen from the frequency analysis table, mode 2 and mode 3 are degenerate as they have the same frequency and in turn the same energy (E=hv).Hence they will appear as one peak. Additionally, mode 5 and mode 6 are degenerate as they also have the same energy and in turn the same infrared absorbtion. Mode 1, Mode 2 and Mode 3 are bonding vibrations and Mode 4, Mode 5 and Mode 6 are stretching vibrations. Mode 4 is a highly symmetric mode. Mode 1 is the vibrational "umbrella mode". Two bands would be observed in the experimental spectrum. Although, Mode 4, Mode 5 and Mode 6 show infrared absorbtions, the intenisty of these infrared absorbtions is incredibly small due to only a very small change in dipole. Hence, these will not be observed on the experimental spectrum. However Mode 1, Mode 2 and Mode 3 will show infrared absorbtions in the experimental spectrum because the vibrational modes involve a significant change in dipole. Furthermore, both Mode 5 and Mode 6 are scissor stretches, therefore as one hydrogen approaches the nitrogen atom, another moves away. Hence, there is no overall change in dipole and in turn no band seen on the experimental spectrum
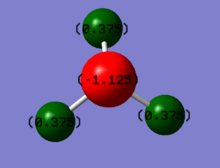
As expected the charge on nitrogen is negative at approximately -1.125 and the charge on each hydrogen is positive at approximately 0.375. This was expected as nitrogen is more electronegative compared to hydrogen hence results in a much greater electron denisty on nitrogen compared to hydrogen. Therefore, nitrogens is expected to be negative as observed in the charge distribution image.
N2 Molecule
N-N Bond Length: 1.105 Angstrom
N-N Bond Angle: 180 degrees
Optimisation
Molecule: Nitrogen Molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -109.52412868 a.u.
RMS Gradient: 0.00000365
Point Group Dinfh
Nitrogen |
click here for link to fully optimised N2 molecule
Item-Table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000002 0.001800 YES RMS Displacement 0.000003 0.001200 YES
As shown by the item table, the structure has converged.
| Mode | Frequency | Infrared |
|---|---|---|
| 1 | 2457.31 | 0.000 |
There is no negative frequencies which indicates that the molecule has been fully optimised.
H2 Molecule
H-H Bond Length: 0.743 Angstrom
H-H Bond Angle: 180 degrees
Optimisation
Molecule: Hydrogen Molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -1.17853930 a.u.
RMS Gradient 0.00012170
Point Group Dinfh
Hydrogen |
click here for link to fully optimised H2 molecule.
Item-Table
Item Value Threshold Converged? Maximum Force 0.000211 0.000450 YES RMS Force 0.000211 0.000300 YES Maximum Displacement 0.000278 0.001800 YES RMS Displacement 0.000393 0.001200 YES
As shown by the item table, the structure has converged.
| Mode | Frequency | Infrared |
|---|---|---|
| 1 | 4461.48 | 0.000 |
There is no negative frequencies which indicates that the molecule has been fully optimised.
The Haber-Bosch Process
The Haber-Bosch process is an industrial process that involves the formation of ammonia (NH3). The reaction is given as follows: N2 + 3H2 --> 2NH3
The energy of this reaction can be determined.
E(NH3) =
2*E(NH3)= -56.55776873 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853930 a.u.
3*E(H2)= -3.5356179 a.u.
Change in energy= [(-113.11553746)] - [(-109.52412868)+(-3.5356179)] = -0.05579088 a.u.
Change in energy = -146.47 kJ/mol
The reaction is exothermic and is carried out at high temperatures and pressure in order to shift equilibrium right and hence maximise yield of ammonia.
CH4 Molecule
Optimisation
C-H Bond Length = 1.07 H-C-H Bond Angle = 35.26
Molecule: Methane
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -40.52401404 a.u.
RMS Gradient: 0.00003263
Point Group: Td
Methane |
click here for link to fully optimised CH4 Molecule
Item-Table
Item Value Threshold Converged? Maximum Force 0.000063 0.000450 YES RMS Force 0.000034 0.000300 YES Maximum Displacement 0.000179 0.001800 YES RMS Displacement 0.000095 0.001200 YES
As shown by the item table, the structure has converged.
| Mode | Frequency | Infrared |
|---|---|---|
| 1 | 1356.20 | 14.1008 |
| 2 | 1356.20 | 14.1008 |
| 3 | 1356.20 | 14.1008 |
| 4 | 1578.58 | 0.0000 |
| 5 | 1578.58 | 0.0000 |
| 6 | 3046.46 | 0.0000 |
| 7 | 3162.33 | 25.3343 |
| 8 | 3162.33 | 25.3343 |
| 9 | 3162.33 | 25.3343 |
There is no negative frequencies which indicates that the molecule has been fully optimised.
According to the 3N-6 rule, nine vibratonal modes are expected. Mode 1, Mode 2 and Mode 3 are all degenerate as they all show equal frequencies and hence equal energies (E=hv). Mode 4, Mode 5 and Mode 6 are also degenerate as they show equal energies. Finally, Mode 7, Mode 8 and Mode 9 are all degenerate due to the same reason again. Mode 1, Mode 2, Mode 3, Mode 4 and Mode 5 are all bending vibrations. Mode 6, Mode 7, Mode 8 and Mode 9 are stretching vibrations. Mode 6 is highly symmetrical. Mode 1 is the "umbrella" mode. Mode 1, Mode 2 and Mode 3 involve a change in dipole hence a band is seen in the experimental spectrum. No band is seen for Mode 4 and Mode 5 because there is no change in dipole in the bending vibration. This is because as two of the hydrogens move towards carbon, two hydrogens move away and in turn results in no overall change in dipole. Mode 6 also does not show a band on the experimental spectrum because the stretch is symmetric, hence there is no change in dipole. Mode 7,8 and 9 will show a single band on the experimental spectrum as they all have the same frequency and in turn the same energy. All the modes involve a change in dipole since the stretch is assymetric hence a band will appear on the experimental spectrum.
Molecular Orbitals
This is a non bonding molecular orbital of carbon which represents the core electrons of carbon which has been formed from the 1s atomic orbital of carbon. This non-bonding molecular orbital is very deep in energy and is occupied by two electrons from carbon. Since it is a non bonding orbital, it will have no effect on the bonding in methane.
This is a bonding orbital. This bonding orbital is formed by the overlap of the 1s atomic orbital of hydrogen and 2s atomic orbital of carbon within methane. This molecular orbital is deep in energy and is occupied by two electrons, one electron from the 2s orbital of carbon and one electron from the 1s orbital of hydrogen.
This is a molecular bonding orbital. This bonding orbital is formed by the overlap of the 1s atomic orbital of hydrogen and 2px atomic orbital of carbon. This molecular orbital is equal in energy to the 2py and 2pz.It is occupied by two electrons, one electron from the 2px orbital of carbon and one electron from the 1s atomic orbital of hydrogen.
This is a molecular bonding orbital. This bonding orbital is formed by the overlap of the 1s atomic orbital of hydrogen and 2py atomic orbital of carbon. This molecular orbital is equal in energy to the 2py and 2pz.It is occupied by two electrons, one electron from the 2px orbital of carbon and one electron from the 1s atomic orbital of hydrogen.
This is a molecular bonding orbital. This bonding orbital is formed by the overlap of the 1s atomic orbital of hydrogen and 2pz atomic orbital of carbon. This molecular orbital is equal in energy to the 2py and 2pz.It is occupied by two electrons, one electron from the 2px orbital of carbon and one electron from the 1s atomic orbital of hydrogen.
The 2px, 2py and 2pz are all degenerate.
O2 Molecule (Independent Work)
O=O Bond Length: 1.21602 Angstrom O=O Bond Angle: 180 degrees
Optimisation
Molecule: Oxygen Molecule
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy: -150.25742434 a.u.
RMS Gradient: 0.00007502
Point Group Dinfh
Oxygen |
click here for link to fully optimised O2 Molecule
Item Value Threshold Converged? Maximum Force 0.000130 0.000450 YES RMS Force 0.000130 0.000300 YES Maximum Displacement 0.000080 0.001800 YES RMS Displacement 0.000113 0.001200 YES
As shown by the item table, the structure has converged.
| Mode | Frequency | Infrared |
|---|---|---|
| 1 | 1642.74 | 0.0000 |





