Rep:Mod:01361046
Ammonia:
Following the optimization process of an ammonia molecule using GaussView, the optimized bond length of the ammonia molecule was found to be 1.01798A, and the optimized bond angle of the HNH bond was found to be 105.741 degrees. Other values are stated here:
| Calculation Type | Calculation Method | Basis Set | Charge | Spin | E(RB3LYP) (a.u.) | RMS Gradient
(a.u.) |
Imaginary Freq | Dipole Moment (Debye) | Point Group |
|---|---|---|---|---|---|---|---|---|---|
| FREQ | RB3LYP | 6-31G(d.p) | 0 | Singlet | -56.55776871 | 0.00000485 | 0 | 1.8466 | C3V |
Further values of optimized ammonia are shown below.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
The link below is a .LOG file for the optimized ammonia molecule.
The interactive picture shown below is for an optimized ammonia molecule.
An Optimised Ammonia Molecule |
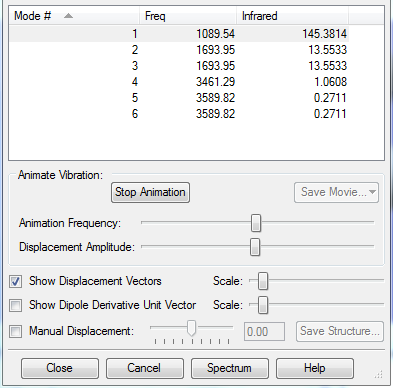
The vibration values of an optimized ammonia molecule are shown below.
Key questions about the optimized ammonia molecule are answered below. How many modes do you expect from the 3N-6 rule?
6 vibrational modes are expected from this rule, as there are four atoms in an ammonia molecule, and 3(4)-6 is equal to 6 different modes.
Which modes are degenerate?
Using the equation: Energy=Frequency x Wavelength, the vibrational modes of equal frequency have the same energy, and are degenerate, and in an ammonia molecule, modes 2 and 3, along with modes 5 and 6, are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Bending vibrations occur at lower energies compared to stretching vibrations, and so modes 1, 2 and 3 are bending vibrations, and modes 4, 5 and 6 are stretching vibrations.
Which mode is highly symmetric?
Vibrational modes 1 and 4 are highly symmetrical.
One mode is known as the "umbrella" mode, which one is this?
Vibrational mode 1 is known as the 'umbrella' mode.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
Even though four different bands would be seen in an experimental spectrum of gaseous ammonia, because two modes are degenerate, only the first two bands are significant in the spectra, as the others do not produce a large a large dipole moment change to be considered as significant.
Leading on from the points stated, following charge analysis on the optimized ammonia molecule, the approximate values of charge on the N atom was calculated to be -1.125, and that for each H atom was found to be +0.375. These values are in accord of expectations because the the N atom is more electronegative than the H atoms, and as the ammonia molecule is neutral, the N atom should have a charge value three times greater than the charge value of the H atom, as found using GaussView.
Nitrogen:
On the other hand, following optimisation of a nitrgoen molecule, the optimised bond length was found to be 1.10550A. The molecule is also linear, and so the bond angle of the NN bond is 180 degrees. Other values are stated here:
| Calculation Type | Calculation Method | Basis Set | Charge | Spin | E(RB3LYP) (a.u.) | RMS Gradient
(a.u.) |
Imaginary Freq | Dipole Moment (Debye) | Point Group |
|---|---|---|---|---|---|---|---|---|---|
| FREQ | RB3LYP | 6-31G(d.p) | 0 | Singlet | -109.52412868 | 0.02473091 | 0 | 0 | D*H |
Further values of optimized nitrogen are shown below.
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
The link below is a .LOG file for the optimized nitrogen molecule.
The interactive picture shown below is for an optimized nitrogen molecule, showing two nitrogen molecules for clarity.
An Optimised Nitrogen Molecule |
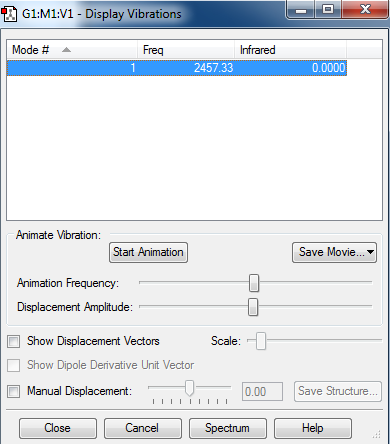
The vibration values of an optimized nitrogen molecule are shown below. The diatomic molecule only has one vibrational mode following the equation 3N-6 for the different number of vibrational modes possible.. Also, there are no peaks in the IR spectrum as no vibrations lead to a change in dipole moment of the molecule.
Hydrogen:
Furthermore, following optimisation of a hydrogen molecule, the optimised bond length was found to be 0.74279A. The molecule is also linear, and so the bond angle of the HH bond is 180 degrees. Other values are stated here:
| Calculation Type | Calculation Method | Basis Set | Charge | Spin | E(RB3LYP) (a.u.) | RMS Gradient
(a.u.) |
Imaginary Freq | Dipole Moment (Debye) | Point Group |
|---|---|---|---|---|---|---|---|---|---|
| FREQ | RB3LYP | 6-31G(d.p) | 0 | Singlet | -1.17853936 | 0.09719500 | 0 | 0 | D*H |
Further values of optimized hydrogen are shown below.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
The link below is a .LOG file for the optimized hydrogen molecule.
The interactive picture shown below is for an optimized hydrogen molecule, showing two hydrogen molecules for clarity.
An Optimised Hydrogen Molecule |
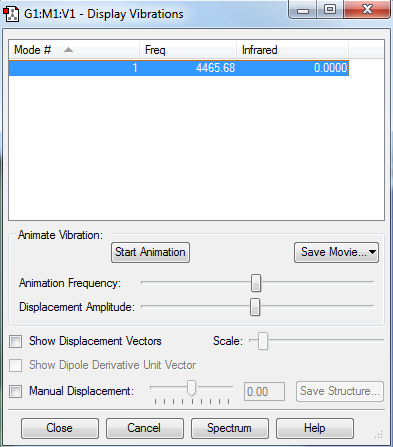
The vibration values of an optimized hydrogen molecule are shown below. The diatomic molecule only has one vibrational mode following the equation 3N-6 for the different number of vibrational modes possible.. Also, there are no peaks in the IR spectrum as no vibrations lead to a change in dipole moment of the molecule.
Further analysis of the ammonia, nitrogen and hydrogen molecules:
Some important energy values have been stated below, with all energy values being in the units of a.u.:
E(NH3)= -56.55776871
2*E(NH3)= -113.11553740
E(N2)= -109.52359111
E(H2)= -1.17853936
3*E(H2)= -3.53561808
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579064
Therefore, in kJ/mol, the energy of the reaction is -146.48, indicating that the products are more reactive than the reactants due to an exothermic reaction taking place. The published energy value of this reaction was found to be -92.38 kJ/mol. [1]
Methane:
Finally, following optimisation of a methane molecule, the optimised bond length was found to be 1.07000A. The molecule is an example of a tetrahedral molecule with a calculated bond angle of 109.471 degrees. Other values are stated here:
| Calculation Type | Calculation Method | Basis Set | Charge | Spin | E(RB3LYP) (a.u.) | RMS Gradient
(a.u.) |
Imaginary Freq | Dipole Moment (Debye) | Point Group |
|---|---|---|---|---|---|---|---|---|---|
| FREQ | RB3LYP | 6-31G(d.p) | 0 | Singlet | -40.52275298 | 0.00803796 | 0 | 0 | T |
Further values of optimized methane are shown below.
Item Value Threshold Converged? Maximum Force 0.000063 0.000450 YES RMS Force 0.000034 0.000300 YES Maximum Displacement 0.000179 0.001800 YES RMS Displacement 0.000095 0.001200 YES
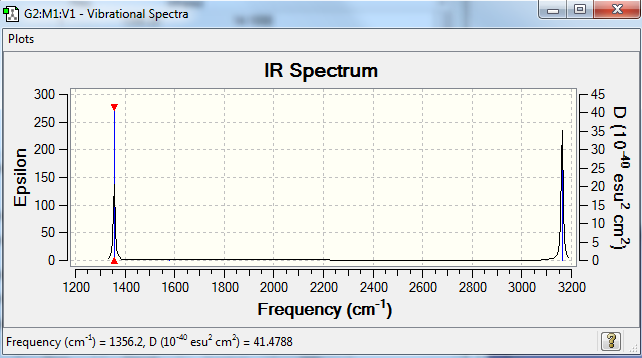
The vibration values of an optimized methane molecule are shown below. Also, the IR spectrum of an optimized methane molecule is also shown below. The IR spectrum obtained using GaussView is as expected using theory, because even though there are nine different vibrations, there are 3 degenerate orbitals, and three vibrations do not absorb in the infrared region as the change in dipole moment is not strong enough to be detected, so do not show in the final spectrum obtained, so there should only be two bands in the final spectrum obtained. These are the only vibrations that result in a change in dipole moment for the methane molecule, and so are seen in the spectra.
The interactive picture shown below is for an optimized methane molecule.
An Optimised Methane Molecule |
The link below is a .LOG file for the optimized methane molecule.
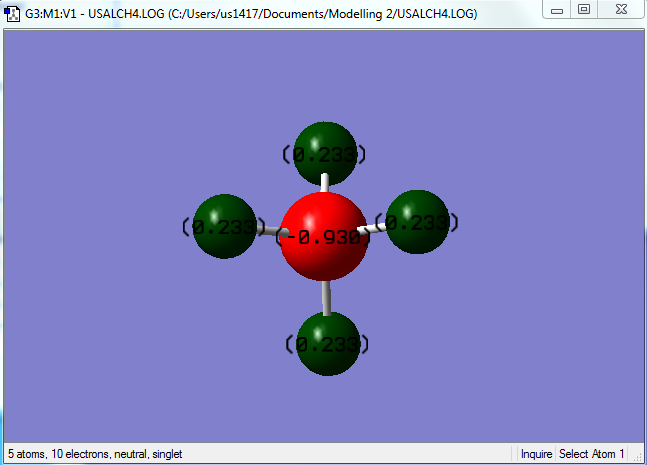
The picture shown below shows the atomic charges carried by the central carbon atom along with the attached hydrogen atoms, as obtained using GaussView.
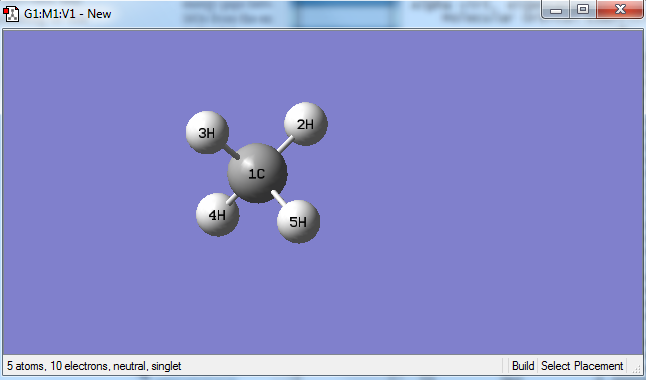
In order to aid with the explanations from the lower section, a labelled methane molecule is shown below.
Moreover, selected MOs are shown below:
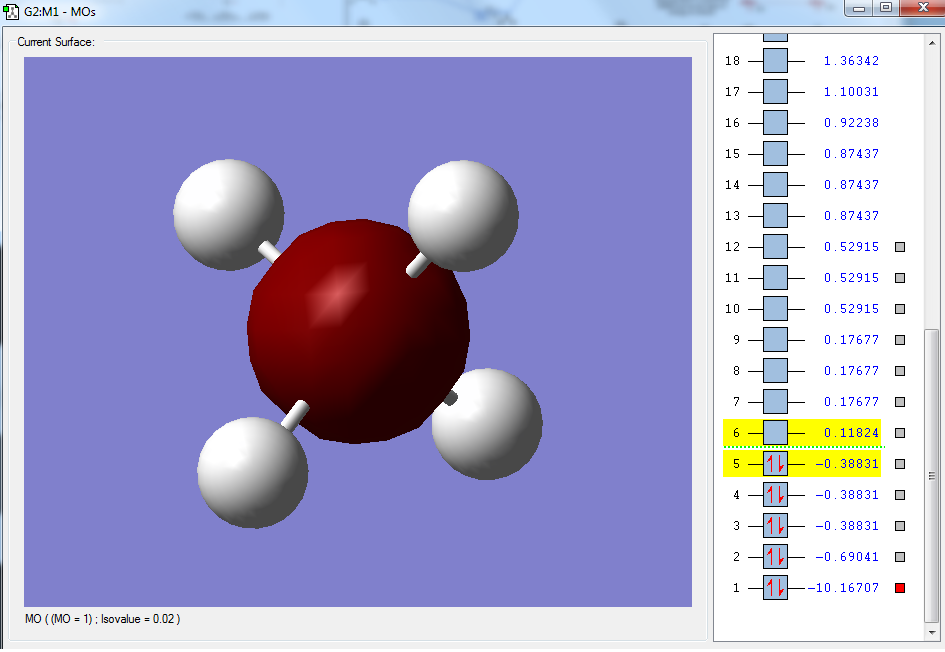
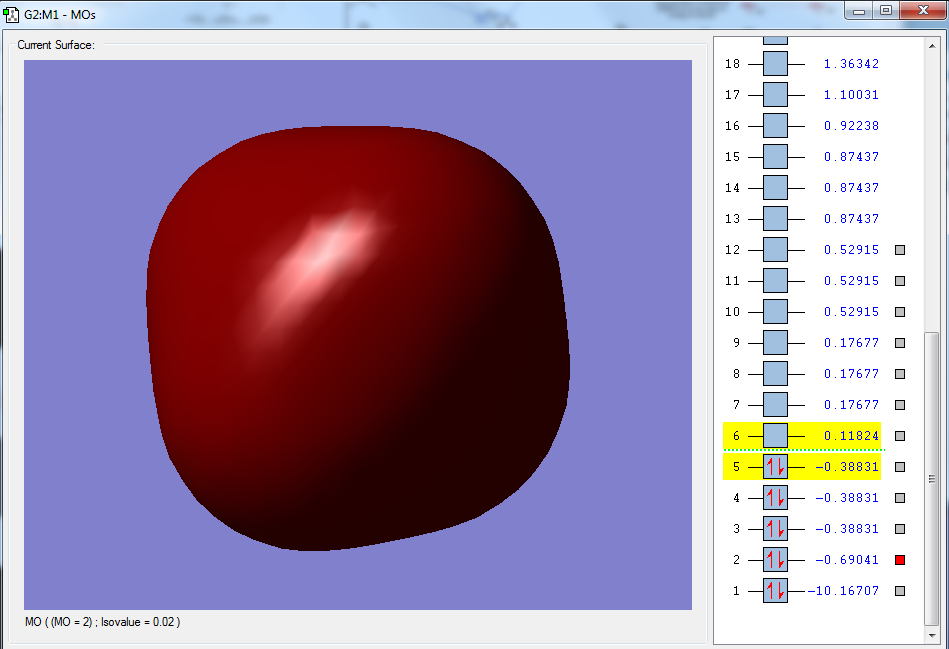
The first molecular orbital, as shown above, has the largest contribution from the 1s orbital of the carbon atom, with a MO coefficient value of 0.99279. This is a non-bonding orbital, as it only involves a contribution from the 1s orbital of the carbon atom.
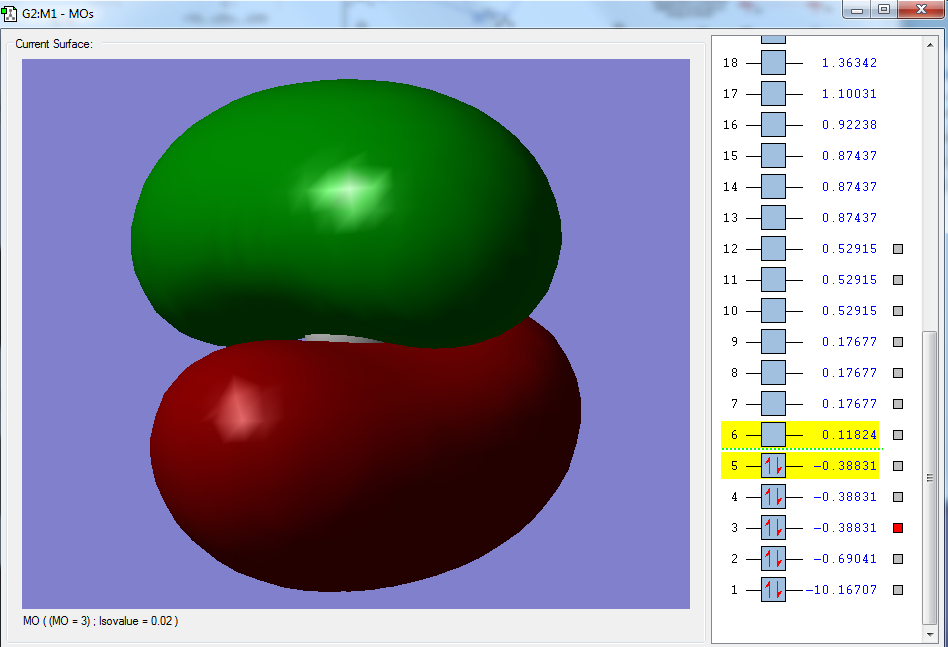
The second molecular orbital, as shown above, has the largest contribution from the 2s orbital of the central carbon atom, with a MO coefficient value of 0.38549. There are also equal contributions from each of the 1s orbitals of the four hydrogen atoms, having a MO coefficient value of 0.14049 each. These atomic orbitals all undergo a linear addition to form the molecular orbitals. This orbital is the linear addition of the 2s orbital of the carbon atom with the four 1s orbitals of the hydrogen atom. The resulting orbital reflects the fact that the electrons of the methane molecule are not specific to a particular bond and are spread across the entire molecule. This is an occupied, bonding orbital that is deep in energy, with published values stating that 25.7eV of energy is required to excite these electrons and remove the electrons from the molecule. This particular MO results in the sigma bonds that hold each carbon atom with the four hydrogen atoms in the methane molecule, and essentially has the largest contribution to its bonding.
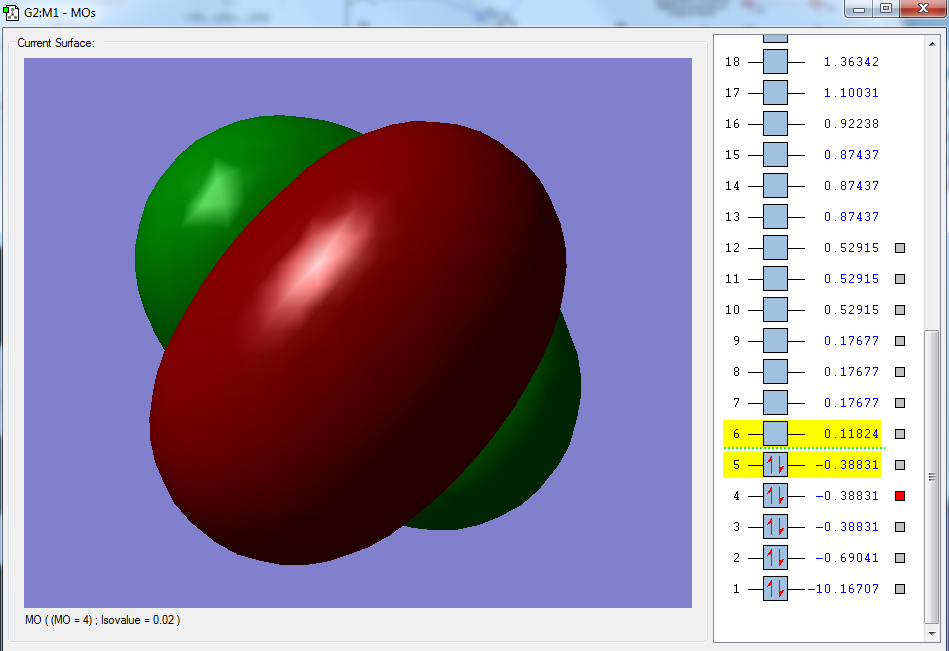
The third molecular orbital, as shown above, is degenerate with the fourth and fifth MOs. This particular orbital has been formed via the addition of the 2PX orbital of the carbon atom, with a MO coefficient value of 0.44629. The two hydrogen orbitals that have a positive contribution to this MO include the hydrogen atoms labelled 2 and 3 from the image shown above. These hydrogen atoms have a MO coefficient value of 0.17082 each. The other two hydrogen orbitals that have a negative contribution to this MO include the hydrogen atoms labelled 4 and 5, which have a MO coefficient value of -0.17082 each. This is an occupied MO that is involved in bonding and is also deep in energy, with published sources stating that 14.8eV of energy is required to excite these electrons and remove these electrons from the molecule.
The fourth molecular orbital. as shown above, is degenerate with the third and fifth MOs. This particular orbital has been formed via the addition of the 2PY orbital of the carbon atom, with a MO coefficient value of 0.44629. The two hydrogen orbitals that have a positive contribution to this MO include the hydrogen atoms labelled 2 and 4. These hydrogen atoms have a MO coefficient value of 0.17082 each. The other two hydrogen orbitals that have a negative contribution to this MO include the hydrogen atoms labelled 3 and 5, which have a MO coefficient value of -0.17082 each. This is an occupied MO that is involved in bonding and is also deep in energy, with published sources stating that 14.8eV of energy is required to excite these electrons and remove these electrons from the molecule.
The fifth molecular orbital, as shown above, is degenerate with the third and fourth MOs. This particular orbital has been formed via the addition of the 2PZ orbital of the carbon atom, with a MO coefficient value of 0.44629. The two hydrogen atoms labelled 2 and 5. These hydrogen atoms have a MO coefficient value of 0.17082 each. The other two hydrogen orbitals that have a negative contribution to this MO include the hydrogen atoms labelled 3 and 4, which have a MO coefficient value of -0.17082 each. This is an occupied MO that is involved in bonding and is also deep in energy, with published sources stating that 14.8eV of energy is required to excite these electrons and remove these electrons from the molecule.
The molecular orbitals labelled 2, 3, 4 and 5 are examples of bonding orbitals, and reflects the stability and unreactivity of the methane molecule, as the absence of anti-bonding orbitals show that bonds are not easily broken.