Rep:Mod:01354530
NH3 molecule
Optimization
Summary
Molecule: NH3
Calculation Method:RB3LYP
Basis Set: 6-31G(d,p)
Final energy, E(RB3LYP): -56.55776873 a.u.
RMS gradient: 0.00000485 a.u.
Point group: C3V
Output
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Optimized NH3 molecule |
Geometric information
N-H bond distance=1.01798 Angstrom.
H-N-H bond angle= 105.741
Vibration analysis
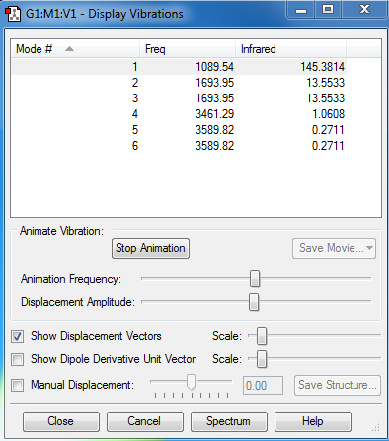
Modes of vibration of NH3 :
No negative vibrations suggests optimization is complete.
IR spectrum of NH3
Analysis
1. I expect 6 modes of vibration from the 3N-6 rule as there are 4 different atoms.
2. Mode 2 and 3, and mode 5 and 6 are degenerate.
3. Modes 1, 2 and 3 correspond to bending vibrations and modes 4,5 and 6 to stretching ones.
4. Mode 4 is highly symmetric, it has no net dipole moment if you take the vector sum.
5. Mode 1 is known as the umbrella mode.
6. I would expect to see 2 bands in an experimental spectrum of gaseous ammonia as for a vibration to show up in an IR spectra it must be IR active, in other words, there must be a change in its dipole moment. As a result, mode 4 would not show up as it is a symmetric vibration and hence the dipoles cancel out. Moreover there are two sets of degenerate orbitals, each set consists of two different vibrations of the same energy and hence would only appear as 1 peak in the IR spectrum. This leaves us with 3 bands: one corresponding to mode 1, another to mode 2 and 3, and the last one to mode 5 and 6. However, the overall change in dipole moment of the degenerate vibrations 5 and 6 is very small when you do a vector sum, leading to very weak intensities in the IR spectra. Consequently, this band would not be seen in an experimental spectrum as it would be hidden by the noise of the spectra. So overall, you would only see 2 clear bands on the experimental IR spectrum of gaseous ammonia.
Atomic charges analysis
Charge on N atom: -1.125
Charge of H atoms: 0.375
My expectations match the result as nitrogen is much more electronegative than hydrogen. As a result, it pulls electron density away from the hydrogens towards itself distorting the electron cloud around them and hence ending up with a partial negative charge on it, leaving the hydrogen atoms with a partial positive one.
H2 molecule
Optimization
Summary
Molecule: H2
Calculation Method:RB3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -1.17853930 a.u.
RMS gradient: 0.00012170 a.u.
Point group: Dinfh
Output
Item Value Threshold Converged? Maximum Force 0.000211 0.000450 YES RMS Force 0.000211 0.000300 YES Maximum Displacement 0.000278 0.001800 YES RMS Displacement 0.000393 0.001200 YES Predicted change in Energy=-5.852867D-08 Optimization completed.
Optimized H2 molecule |
Geometric information
H-H bond distance= 0.74309Angstrom.
H-H bond angle= 180
Vibration Analysis
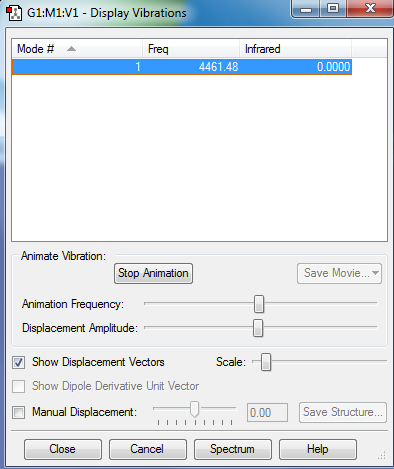
Modes of vibration of H2 :
Hydrogen is a homopolar diatomic molecule and therefore will only have one mode of vibration which corresponds to a symmetric stretch. It will not show up in an IR spectrum as there is no net change in dipole moment.
Atomic charges analysis
Charge of H atoms: 0.000
Results match the expectations as it is a homopolar molecule, in other words, both atoms are the same and hence are as electronegative. Each atom pulls the electron cloud to the same extent and hence there is no partial charge on any of them.
N2 molecule
Optimization
Summary
Molecule: H2
Calculation Method:RB3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -109.52412868 a.u.
RMS gradient: 0.00000060 a.u.
Point group: Dinfh
Output
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401026D-13
Optimization completed.
-- Stationary point found.
File:EL917 N2 OPTF POP GJF.LOG
Optimized N2 molecule |
Geometric information
N-N bond distance= 1.10550 Angstrom.
N-N bond angle= 180
Vibration analysis
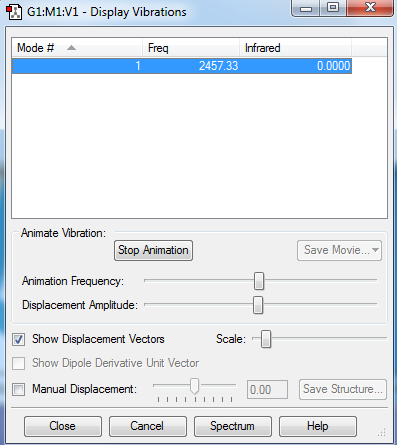
Modes of vibration of N2 :
Atomic charges analysis
Charge of N atoms: 0.000
Again, results match the expectations, as like hydrogen nitrogen is a homopolar molecule. As a result the bond is purely covalent and there is no net charge on either of the atoms.
Evaluating the Haber-Bosch Process
E(NH3)= -56.55776873 a.u.
2*E(NH3)=-113.1155375 a.u.
E(N2)=-109.52412868 a.u.
E(H2)=-1.17853930 a.u.
3*E(H2)=-3.5356179 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.05579092 a.u.
ΔE=-146.48 kJ/mol (to 2.d.p)
The ammonia product is more stable than the gaseous reactants as there is an overall decrease in energy when 2 moles of ammonia are produced from one of nitrogen and three of hydrogen.
S2 molecule
Optimization
Summary
Molecule: S2
Calculation Method:RB3LYP
Basis Set: 6-31G(d,p)
Final energy E(RB3LYP): -796.32599779 a.u.
RMS gradient: 0.00000670 a.u.
Point group: Dinfh
Output
Item Value Threshold Converged?
Maximum Force 0.000012 0.000450 YES
RMS Force 0.000012 0.000300 YES
Maximum Displacement 0.000020 0.001800 YES
RMS Displacement 0.000028 0.001200 YES
Predicted change in Energy=-2.290670D-10
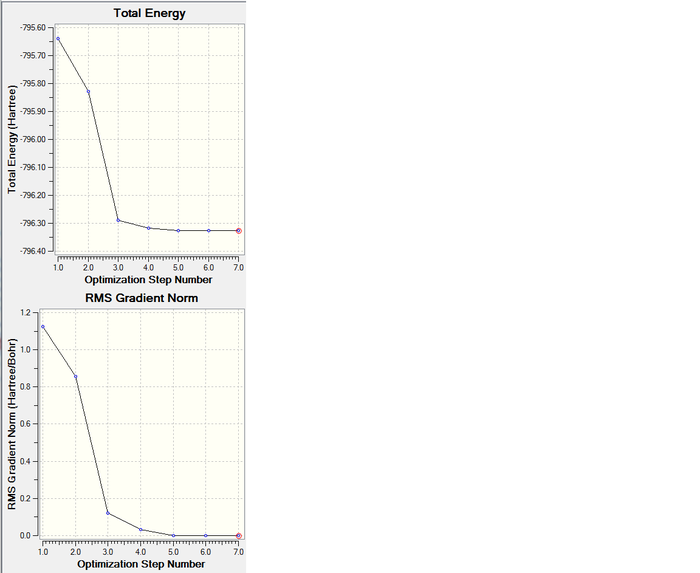
Optimization completed.
-- Stationary point found.
The energy and gradient of the intermediate structures go down towards the optimized structure. The last structure has the lowest energy and smallest gradient, hence, this is the optimized structure.
Optimized S2 molecule |
Geometric information
S=S bond distance= 1.92947 Angstrom.
H-H bond angle= 180
Vibration Analysis
Modes of vibration of S2 :
As expected there is only one vibration mode and it is not IR active as there is no overall change in dipole since the vector sum of these is 0 (it is a symmetrical stretch). As a result, there is no band seen in the IR spectrum of S=S due to its homopolar nature.
Atomic charges analysis
Charge of S atoms: 0.000
Again, it is a homopolar diatomic molecule and therefore there is no dipole as both atoms pull the electron density to the same extent.
S2 Molecular Orbitals
The electronic configuration of a sulfur atom is 1s2 2s2 2p6 3s2 3p4. When 2 atoms combine to form S2, the atomic orbitals(AO) combine to form molecular orbitals(MO).
Non-bonding 2p orbitals of each sulfur atom
This molecular orbital is a non-bonding combination of two of the 2p core atomic orbitals on the sulfur atoms. This MO is much deeper in energy(-5.96349 au) than the MO formed from valence shell AOs, as the 2p AOs are held very closely to their respective nuclei and hence hardly overlap, so they do not take part in bonding.
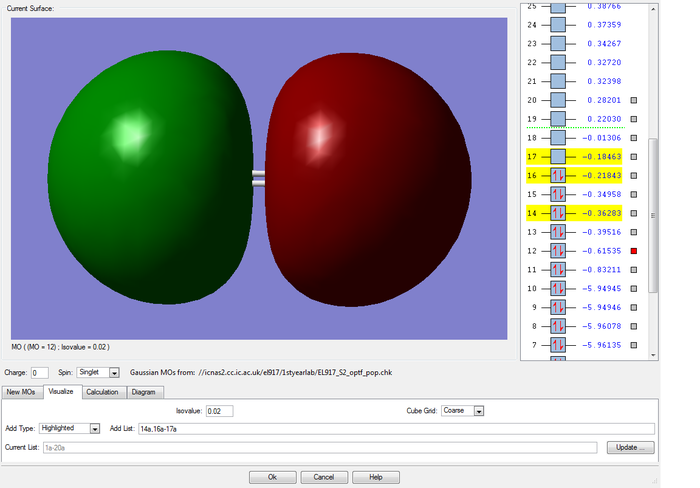
MOs of the bonding and anti-bonding combinations of the two 3s AO on the sulfur atoms
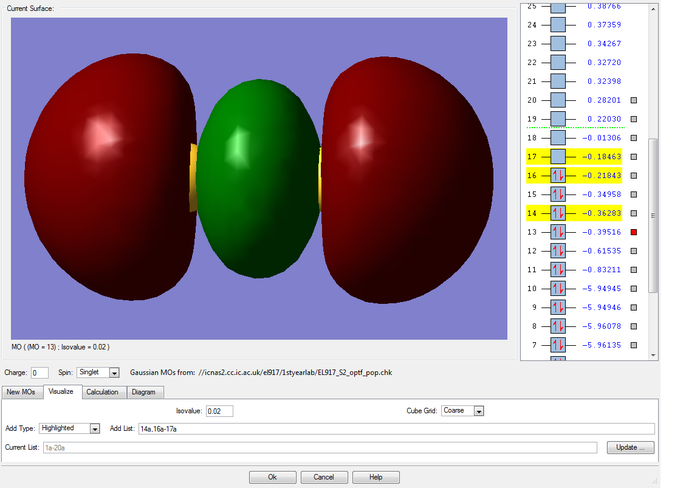
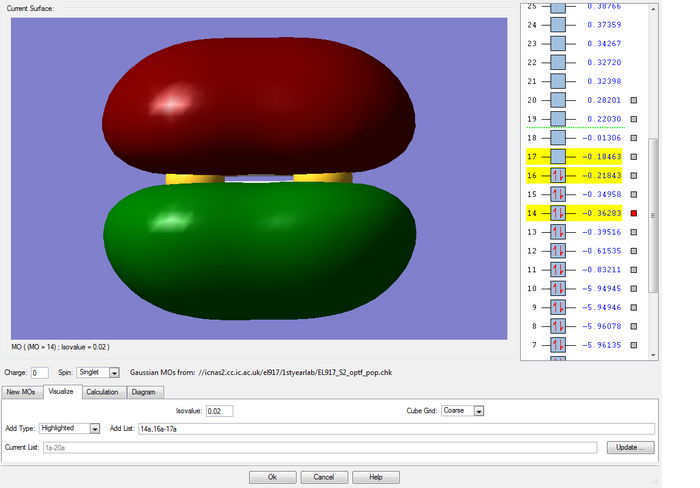
The 3s valence atomic orbitals on each sulfur atom combine to form strong bonding and anti-bonding orbitals.The 3s atomic orbitals are not held as tightly to the nuclei and hence they appreciate a much greater overlap. In fact, the overlap is so extensive that all we see is one extended surface for the bonding orbital.As result, the energy difference between the bonding and anti bonding orbitals is now much grater and they are much higher in energy (-0.83211 and -0.61535 respectively).

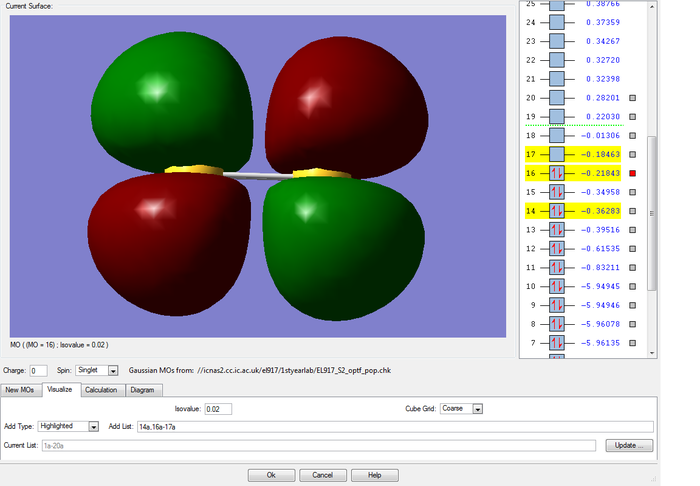
MOs of the sigma and pi bonding combinations of two of the 3p AO on each sulfur atom
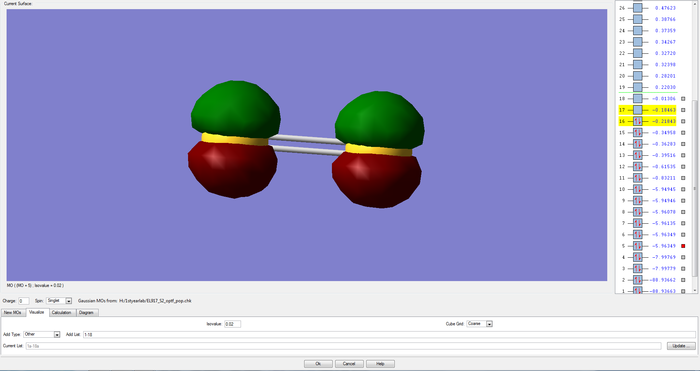
The 3p atomic orbitals can either combine end on to form a sigma bonding molecular orbital along the inter-nuclear axis or, can overlap sideways to form a pi bonding molecular orbital perpendicular to the inter-nuclear axis. The sigma bonding is stronger as there is a better overlap of the orbitals and therefore is deeper in energy (-0.39516 compared to -0.36283 for the pi bond). Because there are two 3p orbitals on each atom that are perpendicular to the bond, we know by symmetry that we should get two molecular pi bonding orbitals of the same energy (degenerate). For some reason Gaussview did not calculate these to be the same energy (-0.36283 and -0.34958).
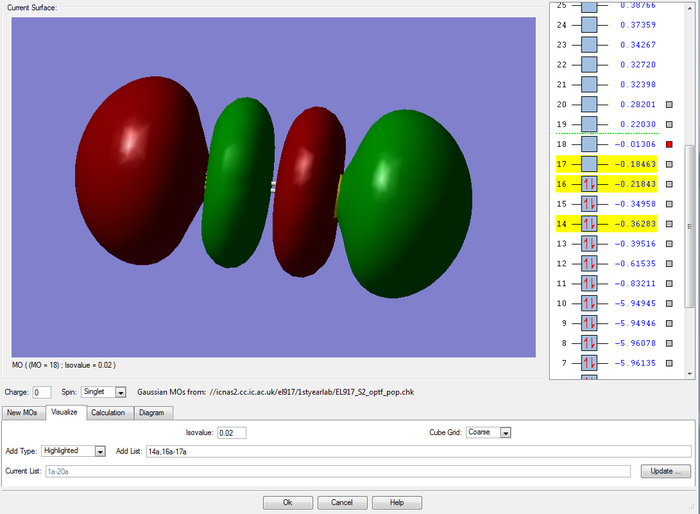
MOs of the pi and sigma antibonding combinations of two of the 3p AO on each sulfur atom
Again, as the sigma overlap is greater than the pi, the difference in energy between the bonding and antibonding orbitals is larger, leading to the sigma antibonding orbital being higher in energy than the pi one in this case (-0.18463au compared to -0.21843au). The pi antibonding molecular orbital formed from the two 3p orbitals forms the highest occupied molecular orbital and the corrresponding sigma MO forms the lowest unoccupied molecular orbital.