Rep:Mod:01349769
Ammonia (NH3)
Summary Information
| Optimised N-H Bond Length | 1.02 angstroms |
| Optimised H-N-H Bond Angle | 106 degrees |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -56.55776873 a.u. |
| RMS Gradient Norm | 0.00000485 a.u. |
| Point Group | C3V |
Item Table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
The optimisation file is linked here
Dynamic Image
Optimised Ammonia (NH3) Molecule |
Frequency Analysis & Vibrational Animations
| Wavenumber (cm-1) | 1090 | 1694 | 1694 | 3461 | 3590 | 3590 |
| Symmetry | A1 | E | E | A1 | E | E |
| Intensity (arbitrary units) | 145 | 14 | 14 | 1 | 0 | 0 |
| Image |  |
 |
 |
 |
 |
|
Question & Answer
Q: How many modes do you expect from the 3N-6 rule?
A: The number of vibrational modes expected from the 3N-6 rule is 3(4)-6 = 6 vibrational modes.
Q: Which modes are degenerate(ie have the same energy)?
A: The two vibrational modes with a wavenumber of 1694cm-1 are degenerate and the other two vibrational modes with a wavenumber of 3590cm-1 are degenerate as well.
Q: Which modes are "bending" vibrations and which are "bond stretch" vibrations?
A: The vibrational mode with wavenumber 1090cm-1 and the two degenerate vibrational modes with wavenumber 1694cm-1 are bends. The vibrational mode with wavenumber 3461cm-1 and the two degenerate modes with wavenumber 3590cm-1 are stretches
Q: Which mode is highly symmetric?
A: The mode at wavenumber 3461cm-1 is highly symmetric.
Q: One mode is known as the "umbrella" mode, which one is this?
A: Vibrational mode at wavenumber 1090cm-1 is the "umbrella mode".
Q: How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
A: There are six vibrational modes, however two pairs are degenerate (specifically the pairs at wavenumber 1694cm-1 and 3590cm-1. Additionally, the intensity of the mode at 3461cm-1 is very small relative to the bends in the spectrum, due to such a small change in dipole moment. In practice, it's subjective whether this peak would even be noticeable. The modes at wavenumber 3590cm-1 are at 0 intensity, so this won't be seen as a result. Depending on experimental conditions and the quality of spectrometer, three bands may be seen from the vibrations at wavenumbers of 1090cm-1, 1694cm-1 and 3461cm-1 or two bands at wavenumbers 1090cm-1 and 1694cm-1.
Atomic Charges
Charge on nitrogen atom: -1.125
Charge on hydrogen atoms: 0.375
It's expected that there would be a negative charge on the nitrogen atom as it's more electronegative than the hydrogen. Consequently, it will draw electron density towards itself, giving it a negative charge.
Nitrogen (N2)
Summary Information
| Optimised N-N Bond Length | 1.11 angstroms |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -109.52412868 a.u. |
| RMS Gradient Norm | 0.00000060 a.u. |
| Point Group | DInfinityH |
Item Table
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
The optimisation file is linked here
Dynamic Image
Optimised Nitrogen (N2) Molecule |
Frequency Analysis & Vibrational Animations
| Wavenumber (cm-1) | 2457 |
| Symmetry | SGG |
| Intensity (arbitrary units) | 0 |
| Image | 
|
The vibration at wavenumber 2457cm-1 is due to a N-N stretch. However, there is no peak from this vibration because this vibration doesn't result in a change in dipole moment, which is a selection rule for infrared spectroscopy. Thus, the spectrum will be bandless.
Atomic Charges
Charge on both nitrogen atoms: 0.000
This value occurs due to the fact that both atoms are of the same element and have the same electronegativity. They therefore pull in electron density to the same extent and so have the same value of 0.000 as the charge.
Mono-atomic Transition Metal Complex
Unique Identifier: DEKFUX
Link to Structure: https://www.ccdc.cam.ac.uk/structures/search?sid=ConQuest&coden=CEUJED&year=2017&spage=12709&volume=23&id=doi:10.1002/chem.201702727&pid=ccdc:1555410
N-N Bond Length in Transition Metal Complex: 1.086 angstroms N-N Optimised Bond Length in Dinitrogen Molecule: 1.11 angstroms
Calculations show that the transition metal complex contains the shorter N-N bond relative to the dinitrogen N-N bond length. This is usually not the case, as one of the nitrogen atoms will bond to a transition metal ion and any further electron density will enter the pi antibonding molecular orbital of the N-N bond, leading to a longer bond and a smaller bond order. Factors that can give this calculation might be the method of calculation used on Gaussian (RB3LYP), leading to calculations with higher error, since this only gives accurate results to 2dp. Furthermore, packing affects that occur in experiment can compress the N-N bond, leading to a shorter bond length. Additionally, Gaussian assumes the molecule is in a perfect vacuum, where as in experiment, this won't usually be the case.
Hydrogen (H2)
Summary Information
| Optimised H-H Bond Length | 0.74 angstroms |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -1.17853936 a.u. |
| RMS Gradient Norm | 0.00000017 a.u. |
| Point Group | DInfinityH |
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
The optimisation file is linked here
Dynamic Image
Optimised Hydrogen (H2) Molecule |
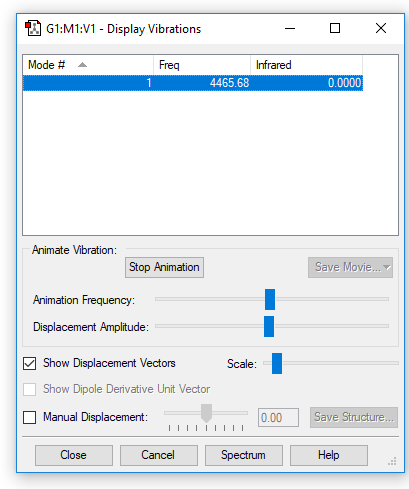
Frequency Analysis & Vibrational Animations
| Wavenumber (cm-1) | 4466 |
| Symmetry | SGG |
| Intensity (arbitrary units) | 0 |
| Image | 
|
The vibration at wavenumber 4466cm-1 is due to a H-H stretch. However, there is no peak from this vibration because this vibration doesn't result in a change in dipole moment, which is a selection rule for infrared spectroscopy. Thus, the spectrum will be bandless.
Atomic Charges
Charge on both hydrogen atoms: 0.000
This value occurs due to the fact that both atoms are of the same element and have the same electronegativity. They therefore pull in electron density to the same extent and so have the same value of 0.000 as the charge.
Haber-Bosch Process Calculation
Energy (NH3) = -56.55776873 a.u.
2* Energy (NH3) = -113.11553746 a.u.
Energy (N2) = -109.52412868 a.u.
Energy (H2) = -1.17853936 a.u.
3* Energy (H2) = -3.53561808 a.u.
ΔE = 2* Energy (NH3)-[Energy (N2)+3* Energy (H2)] = -146.5 kJ/mol
The ammonia product is more stable relative to the reactants.
Oxygen (O2)
Summary Information
| Optimised O-O Bond Length | 1.22 angstroms |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -150.25742434 a.u. |
| RMS Gradient Norm | 0.00007502 a.u. |
| Point Group | DInfinityH |
Item Table
Item Value Threshold Converged? Maximum Force 0.000130 0.000450 YES RMS Force 0.000130 0.000300 YES Maximum Displacement 0.000080 0.001800 YES RMS Displacement 0.000113 0.001200 YES
The optimisation file is linked here
Dynamic Image
Optimised Oxygen (O2) Molecule |
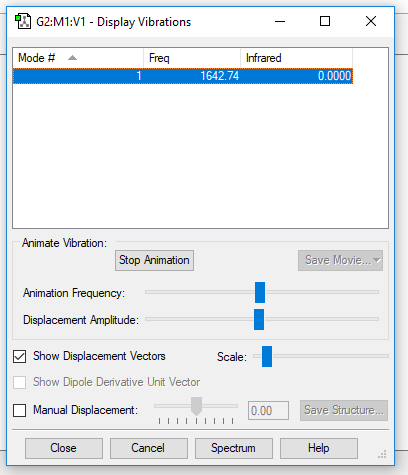
Frequency Analysis & Vibrations
| Wavenumber (cm-1) | 1643 |
| Symmetry | SGG |
| Intensity (arbitrary units) | 0 |
| Image | 
|
The vibration at wavenumber 1643cm-1 is due to an O-O stretch. However, there is no peak from this vibration because this vibration doesn't result in a change in dipole moment, which is a selection rule for infrared spectroscopy. Thus, the spectrum will be bandless.
Atomic Charges
Charge on both oxygen atoms: 0.000
This value occurs due to the fact that both atoms are of the same element and have the same electronegativity. They therefore pull in electron density to the same extent and so have the same value of 0.000 as the charge.
Molecular Orbitals
| Molecular Orbital 1 |  |
This is the lowest lying molecular orbital in terms of energy (-19.30736 a.u.) and is a bonding orbital as the atomic orbitals overlap constructively. It is a sigma type as rotation about any angle along the internuclear axis leaves the wavefunction unchanged. The orbital also has a gerade (g) symmetry label as going from the centre of inversion outwards results in the same phase of orbital. This molecular orbital is specifically formed from the constructive overlap of the 1s orbitals on the oxygen atoms and is fully occupied by two electrons. However, as these are the core orbitals on the atoms, the overlap is very, very poor. The molecular orbital is consequently hardly involved in chemical bonding and as seen from the image, electron density is essentially localised on the two atoms and they are practically non-bonding. |
| Molecular Orbital 2 |  |
This is the HIGHEST occupied molecular orbital (HOMO) and has an energy value of -0.25018 a.u., so relatively high in energy compared to the other occupied molecular orbitals. This is an anti-bonding molecular orbital as the atomic orbitals overlap deconstructively. Rotation about 180 degrees along the internuclear axis leaves the wavefunction changed so this molecular orbital has a pi label. The molecular orbital also has a gerade (g) symmetry label as going from the centre of inversion outwards results in the same phase of orbital. This molecular orbital is specificly formed from the deconstructive overlap of the 2p orbitals on the oxygen atoms and is fully occupied by two electrons. There is good overlap between the two 2p orbitals as they are of the same energy and symmetry. This molecular orbital disrupts chemical bonding as it is anti-bonding and so will reduce bond order and increase bond length, reducing the strength of attraction between the two oxygen atoms. As seen from the image, there is a node in the molecular orbital where there is no electron density to be found, signifying it's anti-bonding nature. |
| Molecular Orbital 3 |  |
This is the LOWEST unoccupied molecular orbital (LUMO) and has an energy value of -0.17928 a.u., so it's higher in energy than any occupied molecular orbital. This is an anti-bonding molecular orbital as the atomic orbitals overlap deconstructively. Rotation about 180 degrees along the internuclear axis leaves the wavefunction changed so this molecular orbital has a pi label. The orbital also has a gerade (g) symmetry label as going from the centre of inversion outwards results in the same phase of orbital. This molecular orbital is specificly formed from the deconstructive overlap of the 2p orbitals on the oxygen atoms and is fully occupied by two electrons. There is good overlap between the two 2p orbitals as they are of the same energy and symmetry. This molecular orbital is essentially the same as Molecular Orbital 2, but in a different spatial orientation (It should be noted that Molecular Orbital 2 and 3 should be degenerate as they are formed from 2p orbitals of the same energy, but due to the calculation method used in the lab, Gaussian didn't recognise this). This molecular orbital doesn't affect chemical bonding in this specific molecule as it is unoccupied, but if it was occupied, it would disrupt chemical bonding as it is anti-bonding and so will reduce bond order and increase bond length, reducing the strength of attraction between the two oxygen atoms. Additionally, if a nucleophile were to react with oxygen, it would attack this molecular orbital so as to break the pi bond and form a sigma bond between itself and an oxygen atom. As seen from the image, there is a node in the molecular orbital where there is no electron density to be found, signifying its anti-bonding nature. |
| Molecular Orbital 4 |  |
This is a relatively low lying molecular orbital in terms of energy (-1.27663 a.u.) and is a bonding orbital as the orbitals overlap constructively. It is a sigma type as rotation about any angle along the internuclear axis leaves the wavefunction unchanged. The orbital also has a gerade (g) symmetry label as going from the centre of inversion outwards results in the same phase. This molecular orbital is specifically formed from the constructive overlap of the 2s orbitals on the oxygen atoms and is fully occupied by two electrons. There is good overlap between these atomic orbitals as they have the same energy and symmetry. The molecular orbital helps chemical bonding in the molecule as it's in the valence shell and increases bond order and hence shortens bond length, thus increasing the attraction between the two oxygen atoms. |
| Molecular Orbital 5 |  |
This is a relatively intermediate molecular orbital in terms of energy (-0.79821 a.u.) and is an anti-bonding molecular orbital as the atomic orbitals overlap deconstructively. It is a sigma type as rotation about any angle along the internuclear axis leaves the wavefunction unchanged. The orbital also has a ungerade (u) symmetry label as going from the centre of inversion outwards results in a different phase of orbital. This molecular orbital is specifically formed from the deconstructive overlap of the 2s orbitals on the oxygen atoms and is fully occupied by two electrons. There is good overlap between these atomic orbitals as they have the same energy and symmetry. This molecular orbital disrupts chemical bonding in the molecule since it's an anti-bonding molecular orbital and does so by decreasing bond order and increasing bond length, thus decreasing the attraction between the two oxygen atoms. |
Chlorine (Cl2) [Independent]
Summary Information
| Optimised Cl-Cl Bond Length | 2.04 angstroms |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy E(RB3LYP) | -920.34987886 a.u. |
| RMS Gradient Norm | 0.00002510 a.u. |
| Point Group | D*H |
Item Table
Item Value Threshold Converged? Maximum Force 0.000043 0.000450 YES RMS Force 0.000043 0.000300 YES Maximum Displacement 0.000121 0.001800 YES RMS Displacement 0.000172 0.001200 YES
The optimisation file is linked here
Dynamic Image
Optimised Chlorine (Cl2) Molecule |
Frequency Analysis & Vibrational Animations
| Wavenumber (cm-1) | 520 |
| Symmetry | SGG |
| Intensity (arbitrary units) | 0 |
| Image | 
|
The vibration at wavenumber 520cm-1 is due to an O-O stretch. However, there is no peak from this vibration because this vibration doesn't result in a change in dipole moment, which is a selection rule for infrared spectroscopy. Thus, the spectrum will be bandless.
Atomic Charges
Charge on both chlorine atoms: 0.000
This value occurs due to the fact that both atoms are of the same element and have the same electronegativity. They therefore pull in electron density to the same extent and so have the same value of 0.000 for the charge.
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 1/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 5/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES - you have dine a really good job! Just one small comment:
You correctly described MO1 and in your text you are deducing it is 'practically non-bonding'. For the next time please label such a MO just as non-bonding. Just because the AOs are combined in an in-phase way it does not necessarily needs to be labelled as a bonding MO.
Independence 1/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or
YES - well done! During the vibrational analysis you are stating once "O-O stretch' but you are looking at CL2. This is probably just a typo from copying and pasting code from the previous section. You argument is still valid for the case of Cl2.
Do some deeper analysis on your results so far