Rep:Mod:01340064
NH3 molecule
Calculation method: RB3YLB
Basis set: 6-31G(d,p)
Final energy: -56.55776873 au
RMS gradient: 0.05399560 au
Point group: C3V
N-H bond length: 1.01798 Å
H-N-H bond angle: 105.741°
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
test molecule |
The optimisation file is linked to here
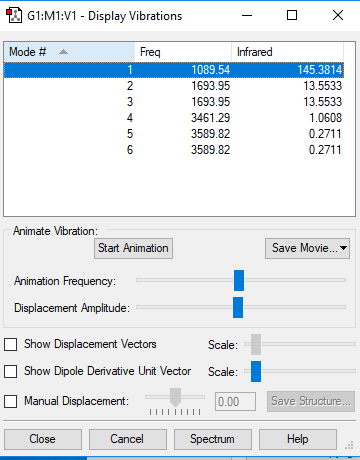
Display Vibrations
How many modes do you expect from the 3N-6 rule?
There are 3 atoms in NH3 (N=6). There are therefore 6 modes expected from the 3N-6 rule.
Which modes are degenerate (i.e have the same energy)?
Modes 2 and 3 Modes 5 and 6
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
Modes 1, 2 and 3 are "bending" vibrations. Modes 4,5 and 6 are "stretching" vibrations.
Which mode is highly symmetric?
Mode 4
One mode is known as the "umbrella" mode, which one is this?
Mode 1
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
Two
Charge on Nitrogen: -1.125 C
Charge on Hydrogen: 0.375 C
Nitrogen is more electronegative than hydrogen, meaning it is more able to attract the electrons in the covalent bonds. Nitrogen is therefore expected to have a partial negative charge and hydrogen is expected to have a partial positive charge.
N2 molecule
Calculation method: RB3YLB
Basis set: 6-31G(d,p)
Final energy: -109.52359111 au
RMS gradient: 0.02473091 au
Point group: Dh∞
N-N bond length: 1.09200 Å
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
test molecule |
The optimisation file is linked to here
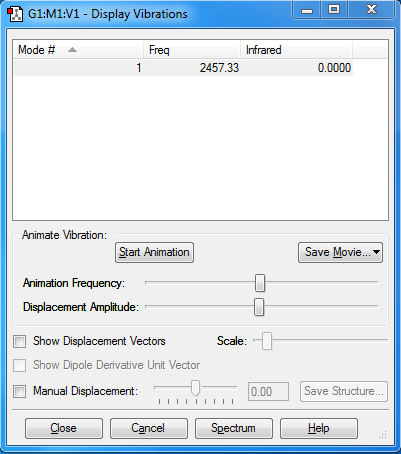
Display Vibrations
1 mode is expected from the 3N-5 rule. (3N-5 is used because molecule is linear).
H2 molecule
Calculation method: RB3YLB
Basis set: 6-31G(d,p)
Final energy: -1.17853936 au
RMS gradient: 0.00000017 au
Point group: Dh∞
H-H bond length: 0.74279 Å
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
test molecule |
The optimisation file is linked to here
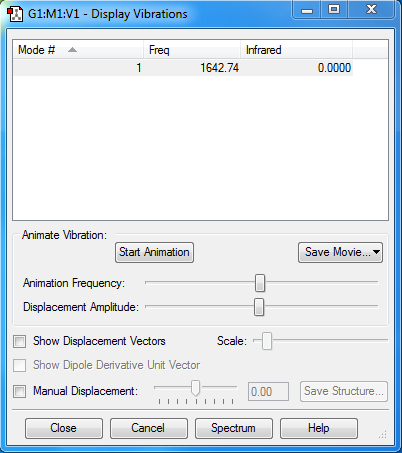
Display Vibrations
1 mode is expected from the 3N-5 rule. (3N-5 is used because molecule is linear).
Energies of Haber-Bosch Process
E(NH3)= -56.55776873 au
2*E(NH3)= -113.1155375 au
E(N2)= -109.52359111 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05632827 a.u = -147.89 kJ/mol
The gaseous reactants are more stable than the ammonia product.
Oxygen
Calculation method: RB3YLB
Basis set: 6-31G(d,p)
Final energy: -150.25742434 au
RMS gradient: 0.00007502 au
Point group: Dh∞
O-O bond length: 1.21602 Å
Item Value Threshold Converged? Maximum Force 0.000130 0.000450 YES RMS Force 0.000130 0.000300 YES Maximum Displacement 0.000080 0.001800 YES RMS Displacement 0.000113 0.001200 YES
test molecule |
The optimisation file is linked to here
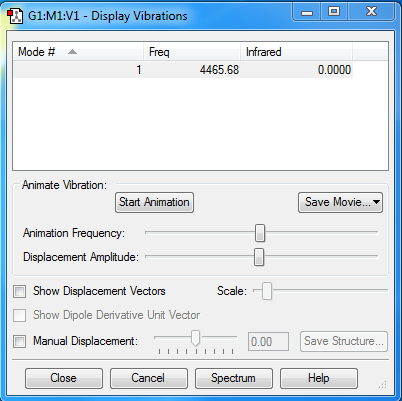
Display Vibrations
The charge on both oxygen atoms is zero
Molecular Orbitals
1σg MO
This MO is formed when the two 1S2 orbitals parallel to the oxygen bond mix in-phase. This is an occupied bonding molecular orbital and is low in energy.
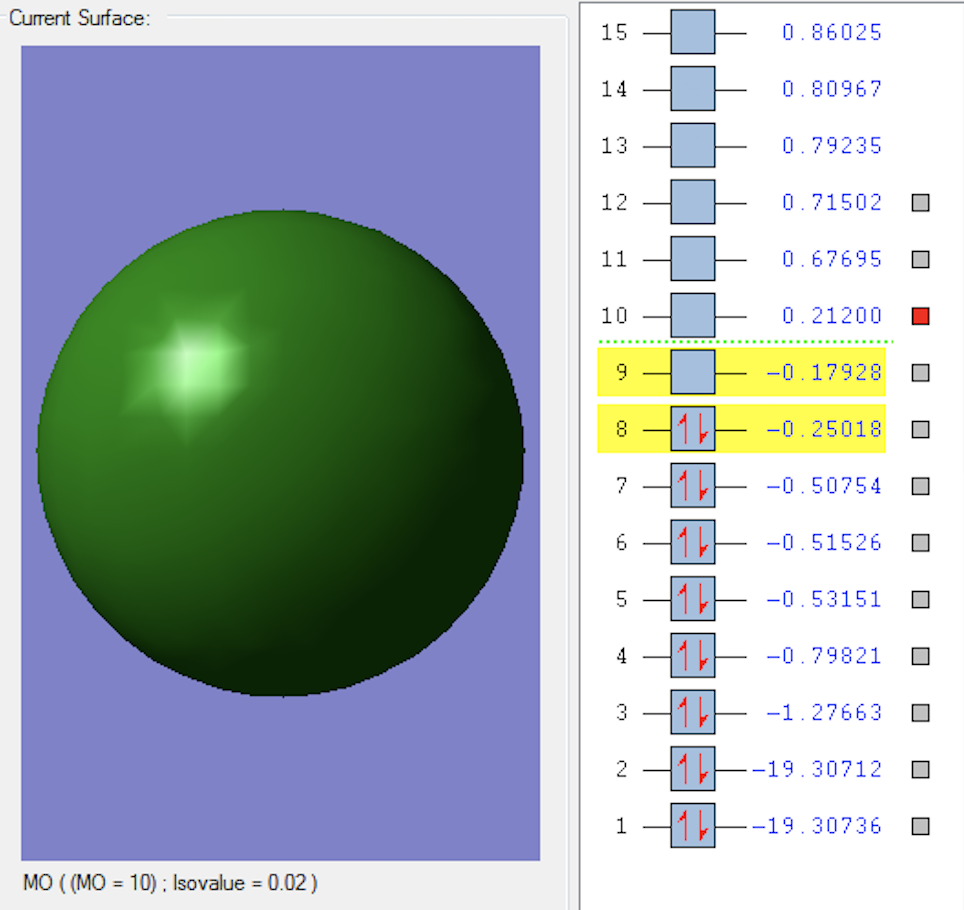
2σ*u MO
This MO is formed when the two 2S2 orbitals parallel to the oxygen bond overlap in anti-phase. This is an occupied anti-bonding orbital which is higher in energy than the previous MO.
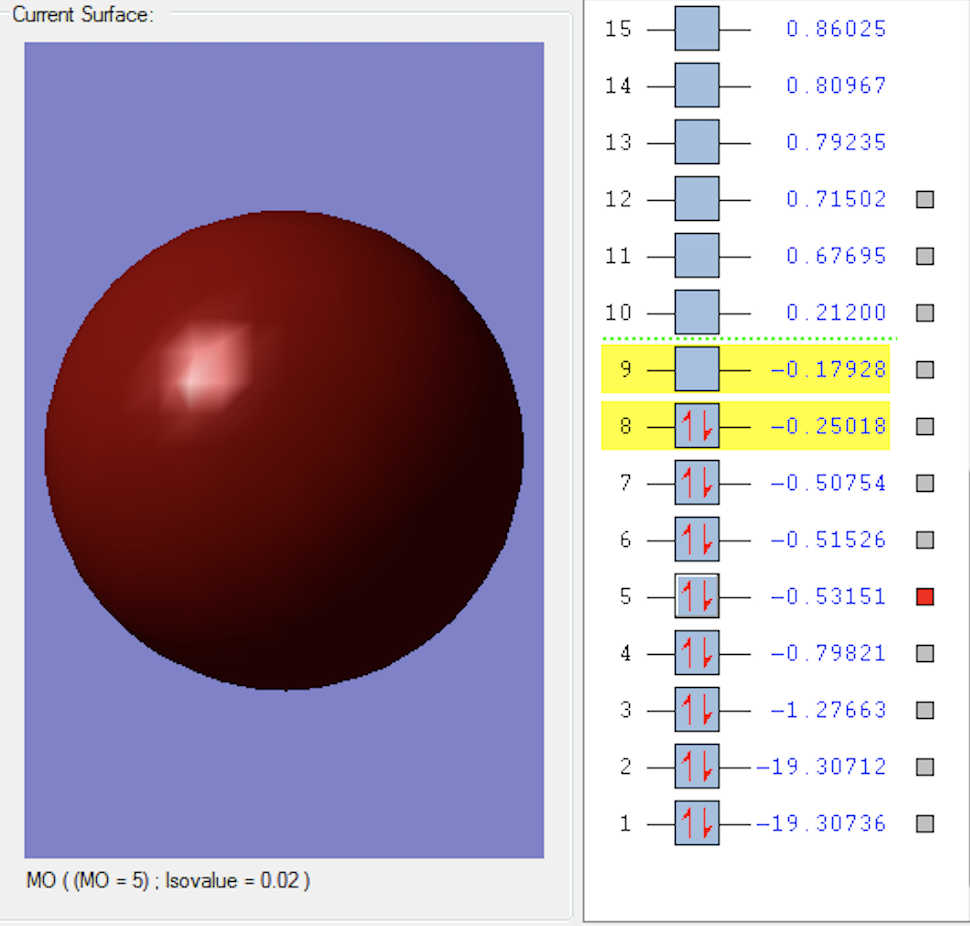
3σg MO
This MO is formed when the two 2px orbitals parallel to the oxygen bond overlap in phase. This is an occupied bonding MO.
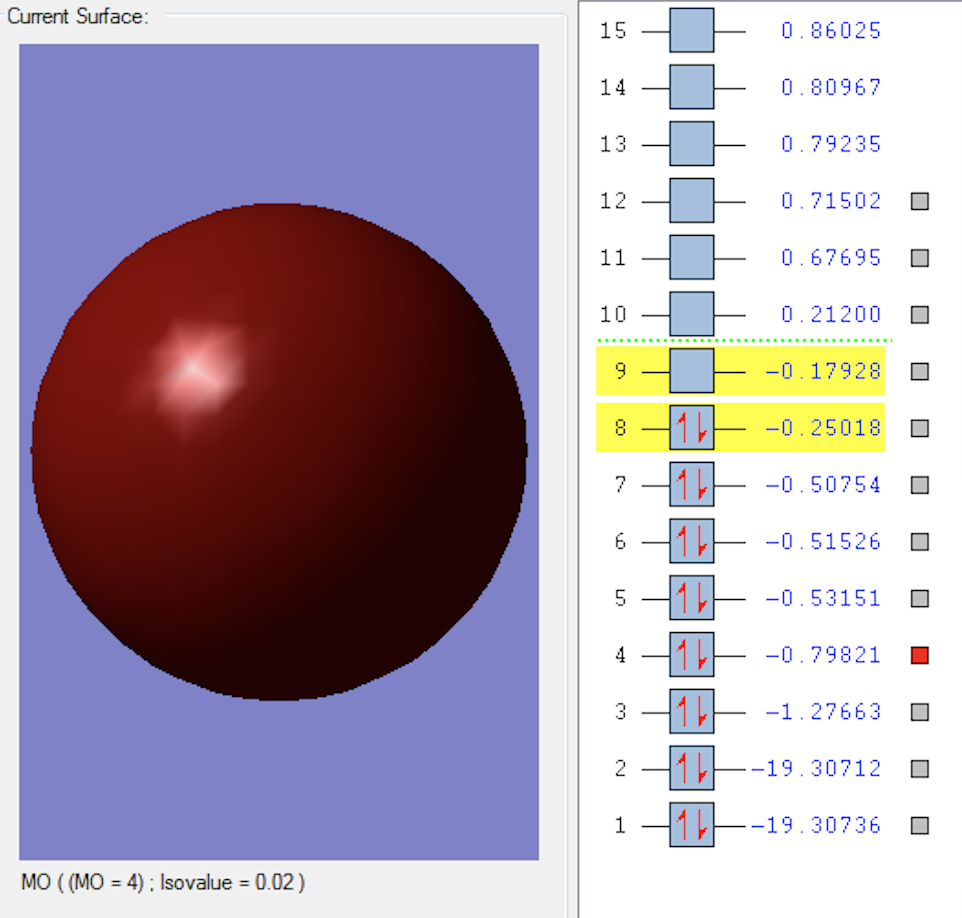
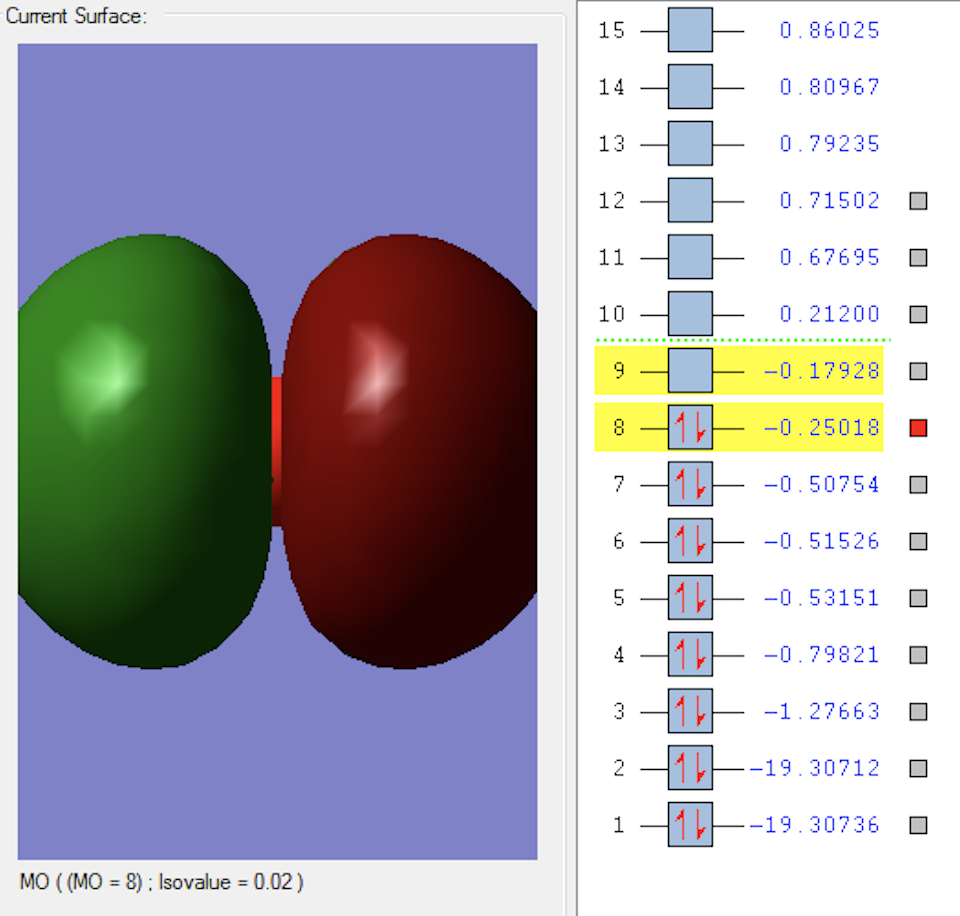
3σ*u MO
This MO is the lowest unoccupied molecular orbital (LUMO) and is formed when the two 2p orbitals parallel to the bond overlap in anti-phase. This is an anti-bonding orbital.
1π*g MO
This MO is the highest occupied molecular orbital (HOMO) and is formed when the two 2py orbitals perpendicular to the bond overlap in anti-phase. This is an anti-bonding orbital.
Independence
Literature values:
Oxygen bond length = 1.21 Å[1]
Hydrogen bond length = 0.74 Å[1]
Nitrogen bond length = 1.45 Å[1]
References
[1] Huheey, pps. A-21 to A-34; T.L. Cottrell, "The Strengths of Chemical Bonds," 2nd ed., Butterworths, London, 1958; B. deB. Darwent, "National Standard Reference Data Series," National Bureau of Standards, No. 31, Washington, DC, 1970; S.W. Benson, J. Chem. Educ., 42, 502 (1965)