Rep:Mod:01336581
Molecular Models 2
Robert Kinnier Wilson 01336581
NH3
Molecule: NH3
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -56.55776873a.u.
RMS gradient: 0.00000485a.u
Point group: C3V
N-H bond distance: 1.018Å
H-N-H bond angle: 105.7°
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986278D-10 Optimization completed.
NH3 |
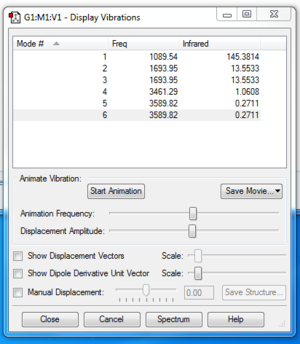
Number of modes from 3N-6: 6. Modes 2&3 and 5&6 are degenerate. These correspond to two bending modes and two stretching modes. Modes 1 to 3 are bending modes, modes 4 to 6 are stretching modes. Mode 4 is highly symmetric. It is the mode with all three N-H bonds stretching equally. Mode 1 is the "umbrella" mode. An experimental IR spectrum of gaseous ammonia will show 2 absorption bands. The other stretches have a change in dipole moment that is too small to discern a peak on an experimental spectrum.
The charge on the hydrogen atoms is +0.375. The charge on the nitrogen is -1.125. This is consistent with expectations, as nitrogen is more electronegative than hydrogen.
N2
Molecule: N2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -109.52412868a.u.
RMS gradient: 0.00000060a.u
Point group: Dinfh
N-N bond length: 1.106Å
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES Predicted change in Energy=-3.400975D-13 Optimization completed.
N2 |
The charge is distributed evenly across the molecule, as the nitrogen atoms have the same electronegativity.
H2
Molecule: H2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -1.17853936a.u.
RMS gradient: 0.00000017a.u.
Point group: Dinfh
H-H bond length: 0.743Å
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
H2 |
The charge is distributed evenly across the molecule, as the hydrogen atoms have the same electronegativity.
Energies of the Haber-Bosch Process
E(NH3)= -56.55776873a.u.
2×E(NH3)= -113.11553746a.u.
E(N2)= -109.52412868a.u.
E(H2)= -1.17853936a.u.
3*E(H2)= -3.53561808a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579070a.u.
ΔE= -146.5kJ/mol
Since the energy change of this reaction is negative, the product (ammonia) must be more stable than the reactants (hydrogen and nitrogen).
A small molecule: Phosphorous
Molecule: P2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy: -682.68894541a.u.
RMS gradient: 0.00000021a.u.
Point group: Dinfh
P-P bond length: 1.904Å
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.816599D-13 Optimization completed.
P2 |
Phosphorous Molecular Orbitals
3σg:
The 3σg is the orbital formed by the bonding overlap between the 2pz orbitals in an end to end manner. Although deeper in energy than the valence orbitals, at -4.74a.u., this orbital has a small influence in bonding, as shown by the small amount of electron density connecting the green lobes along the bond.
4σu*:
The 4σu* is an anti-bonding orbital formed from the out of phase overlap of the 3s orbitals. It has an energy of -0.467a.u. This orbital shows clearly the nodal plane perpendicular to the bond axis that is characteristic of anti-bonding orbitals.
5σg
The 5σg is a bonding orbital formed from the overlap of the 3pz orbitals in a similar way to the 3σg orbital. This orbital it larger than the 3σg orbital, because the 3p atomic orbitals are larger than the 2p atomic orbitals, but of the same form. The 5σg has an energy of -0.298a.u.
2πu
The 2πu orbital is a bonding orbital formed from the overlap of the 3px or 3py orbitals side to side. Since the 3p orbitals are degenerate, the two π orbitals are degenerate as well. This orbital is the HOMO for the molecule, with an energy of -0.287a.u. The HOMO is quite high in energy, which leads to the relative instability of P2 compared to the preferred P4. The nodal plane of this orbital is parallel to the bond axis.
2πg*
The 2πg* orbital is an anti-bonding orbital formed from the overlap of the 3px or 3py orbitals side to side. This orbital is the LUMO for the molecule, with an energy of -0.101a.u. This orbital has two nodal planes; 1 parallel to the bond axis and 1 perpendicular.