Rep:Mod:01221453
NH3 Molecule
Molecule: NH3
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -56.55776873 a.u.
RMS Gradient: 0.00000485 a.u.
Molecule Point Group: C3V
N-H Bond Distance: 1.01798 Angstroms
H-N-H Bond Angle: 105.741 Degrees
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Optimised NH3 |
The optimisation file is linked here
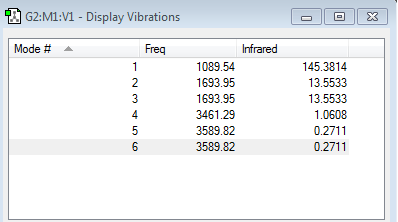
How many modes do you expect from the 3N-6 rule?
6 modes are expected using the 3N-6 rule as in this atom, N=4 since there are 4 atoms.
Which modes are degenerate (ie have the same energy)?
The degenerate modes are 2 and 3, 5 and 6.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
The bending vibrations are the first, second and third modes whilst the fourth, fifth and sixth modes are the bond stretching vibrations.
Which mode is highly symmetric? Mode 4 is highly symmetric.
One mode is known as the "umbrella" mode, which one is this? The umbrella mode is mode 1.
How many bands would you expect to see in an experimental spectrum of gaseous ammonia? In an experimental spectrum of gaseous ammonia, we would expect to see two bands. This is because modes 4-6 are so small, they do not appear as significant peaks on the spectrum. Mode 1 will contribute a large peak and modes 2 and 3 have the same frequency, therefore appearing as the same band on the spectrum.
Charges N: -1.125 H: 0.375 I'd expect the nitrogen atom to be negative as it's more electronegative. Therefore it pulls in the electrons shared with the hydrogens atoms. Due to this, we'd expect the hydrogen atoms to be positive.
N2 Molecule
Molecule: N2
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -109.52412868 a.u.
RMS Gradient: 0.00000060 a.u.
Molecule Point Group: D∞H
The bond length is 1.10550 Angstroms.
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
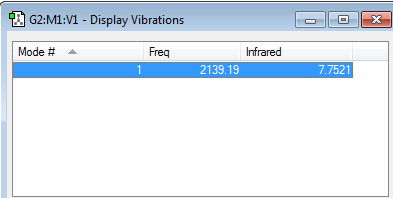
The frequency obtained for the N2 molecule is +2457.33 and there is one mode.
Optimised N2 |
The optimisation file is linked to here
As the molecule is linear, we use the 3N-5 rule to calculate vibration modes, hence why there is only one vibration mode. This is a bond stretching mode.
The atomic charges on the nitrogen atoms is 0.
H2 Molecule
Molecule: H2
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -1.17853936 a.u.
RMS Gradient: 0.00000017 a.u.
Molecule Point Group: D∞H
The bond length is 0.742798 Angstroms.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Optimised H2 |
The optimisation file is linked here
As the molecule is linear, we use the 3N-5 rule to calculate vibration modes, hence why there is only one vibration mode. This is a bond stretching mode.
The atomic charges on the hydrogen atoms is 0.
N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u.
ΔE=-0.0557907*2625.5= -146.48 kj/mol (2d.p)
A literature value for ΔE is -92.44 kJ/mol.[1]
The ammonia product is more stable. Energy is released when ammonia is formed as the formation of ammonia gives out more energy than when absorbed in breaking the nitrogen and hydrogen bonds.
Project Molecule
CN-
Molecule: CN-
Calculation Method: RB3LYP
Basis Set: 6-31G(d.p)
Final Energy E(RB3LYP): -92.82453153 a.u.
RMS Gradient: 0.00000704 a.u.
Molecule Point Group: C∞V
C-N Bond Distance: 1.18409 Angstroms
Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000005 0.001800 YES RMS Displacement 0.000008 0.001200 YES
Optimised CN |
The optimisation file is linked here
CN- is IR active as there's a dipole moment. Using the 3N-5 rule, there's only one vibration mode due to bond stretching, as the bond order (3) restricts the molecule from bending.
As CN- is an anion, there is an overall negative charge. This explains why both the carbon and nitrogen atoms are negative. Nitrogen is the more electronegative atom, therefore is more negative than the carbon atom.
This sigma MO is the 2s bonding orbital as there is high electron density between the 2s AOs. The MO is deep in energy as it's made from the 2s orbitals which are highly penetrating.
This is a sigma anti-bonding MO made from the 2s AOs. The carbon contributes more to the anti-bonding orbital as it's less negative.
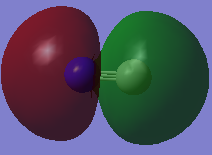
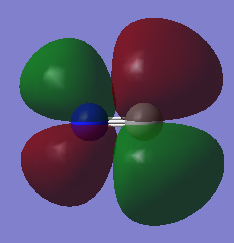
This is the HOMO. It's a sigma bonding MO formed between the 2p AOs. There are anti-bonding areas on either side of the molecule.
A pi bonding orbital formed by 2p AOs. There is another pi orbital orthogonal to this pi orbital which form the triple bond along with the HOMO.
This is the LUMO. It's a pi* anti-bonding MO formed by the 2p AOs. It is high in energy. When occupied, it would cause the bonds to break.
References
2.1 Ammonia Synthesis, Prof. Dr. R. Schlogl, page 7