Rep:Mod:01196400

NH₃ Molecule

Ammonia (NH₃) Properties:

Calculation method = RB3LYP

Basis set = 6-31G(d,p)

Final Energy = -56.55776873 a.u.

RMS gradient = 0.00000485 a.u.

Point group = C_3V

N-H Bond length = 1.01798 Angstrom

H-N-H Bond Angle = 105.741°

"Item" Table

        Item               Value     Threshold  Converged?
Maximum Force            0.000004     0.000450     YES
RMS     Force            0.000004     0.000300     YES
Maximum Displacement     0.000072     0.001800     YES
RMS     Displacement     0.000035     0.001200     YES

NH₃ Jmol

File:OJWA NH3 OPTF POP.LOG

Ammonia Molecule

Vibrational Modes

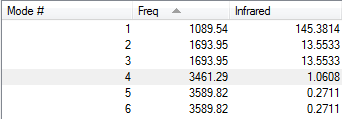
The 3N-6 rule would suggest 6 vibrational mode.

Modes 2 & 3 and 5 & 6 are degenerate.

Modes 1,2 and 3 are bending modes. 4, 5 and 6 are stretching modes.

Mode 4 is highly symmetric. Mode 1 is the "umbrella" mode.

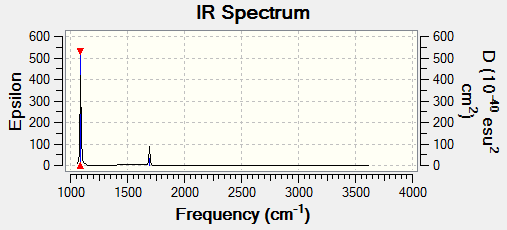
You would expect to see 4 bands in an experimental spectrum of gaseous ammonia.

The peaks at 3461.26cm^-1 and 3589.82cm^-1 have negligible intensities and are therefore not seen on the spectrum.

Charge Distribution

The charge on the hydrogen is expected to be positive and the charge on the nitrogen negative.

The calculated values are:

• -1.125 on N

• 0.375 on H

Haber-Bosch Process

H₂ Molecule

Hydrogen (H₂) Properties:

Calculation method = RB3LYP

Basis set = 6-31G(d,p)

Final Energy = -1.17853936 a.u.

RMS gradient = 0.00000017 a.u.

Point group = D_infH

H-H Bond length = 0.74279 Angstrom

H-H Bond Angle = 180°

"Item" Table

        Item               Value     Threshold  Converged?
Maximum Force            0.000000     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000001     0.001200     YES

H₂ Jmol

File:OJWA H2 OPT.LOG

Hydrogen Molecule

Vibrational Modes

None negative.

Charge Distribution

Purely covalent bond therefore no charge on the hydrogen atoms.

N₂ Molecule

Nitrogen N₂ Properties

Calculation method = RB3LYP

Basis set = 6-31G(d,p)

Final Energy = -109.52412868 a.u.

RMS gradient = 0.00000060 a.u.

Point group = DinfH

N-N Bond length = 1.10550 Angstrom

N-N Bond Angle = 180°

"Item" Table

        Item               Value     Threshold  Converged?
Maximum Force            0.000001     0.000450     YES
RMS     Force            0.000001     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000000     0.001200     YES

N₂ Jmol

File:OJWA N2 OPT.LOG

Nitrogen Molecule

Vibrational Modes

None negative.

Charge Distribution

Purely covalent bond therefore no charge on the nitrogen atoms.

Reaction Energies

N₂ + 3H₂ -> 2NH₃

•E(NH₃)= -56.55776873 a.u.

•2*E(NH₃)= -113.11553746 a.u.

•E(N₂)= -109.52412868 a.u.

•E(H₂)= -1.17853936 a.u.

•3*E(H₂)= -3.53561808 a.u.

•ΔE=2*E(NH₃)-[E(N₂)+3*E(H₂)]= -113.11553746 - (-109.52412868 - 3.53561808) = -0.05579069 a.u.

-0.05579069 Hartrees = -146.48 kJmol^-1

The ammonia product is therefore lower in energy than the gaseous reactants. The product is more stable than the reactants.

CH₄ Molecule

‍Structure

Methane (CH₄) Properties:

Calculation method = RB3LYP

Basis set = 6-31G(d,p)

Final Energy = -40.52401404 a.u.

RMS gradient = 0.00003263 a.u.

Point group = T_d

C-H Bond length = 1.09197 Angstrom

H-C-H Bond Angle = 109.471°

"Item" Table

        Item               Value     Threshold  Converged?
Maximum Force            0.000063     0.000450     YES
RMS     Force            0.000034     0.000300     YES
Maximum Displacement     0.000179     0.001800     YES
RMS     Displacement     0.000095     0.001200     YES

CH₄ Jmol

File:OJWA CH4 OPT.LOG

Methane molecule

Vibrational Modes

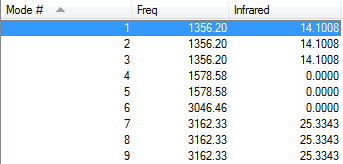
The 3N-6 rule would suggest 9 vibrational modes.

Modes 1, 2 & 3 are degenerate. As are 4 & 5 and 7, 8 & 9.

1, 2, 3, 4, 5 & 6 are bending modes. 6, 7, 8 & 9 are stretching modes.

Mode 6 is highly symmetric.

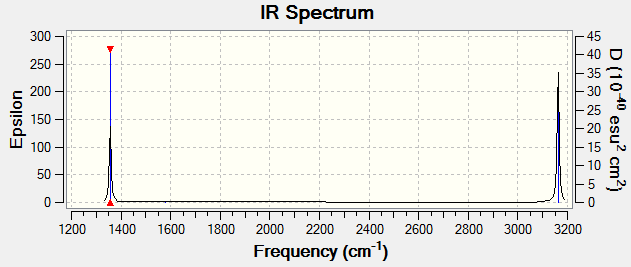
You would expect to see 2 peaks in an experimental spectrum of gaseous methane.

Charge Distribution

You would expect the carbon to have a negative charge and the hydrogen a positive charge.

Calculated values:

•Carbon = -0.930

•Hydrogen = 0.233

CH₄ Molecular Orbitals

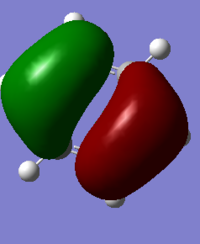
MO 1

This MO is very deep in energy (-10.16707 Hartrees).

This is a non-bonding orbital and therefore has no contribution to the bonding of the structure. It is from the 1s orbital of the carbon.

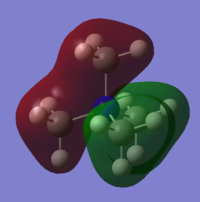
MO 2

This MO is deep in energy (-0.69041 Hartrees).

This is a bonding orbital formed from the hybridization of the hydrogen's 1s orbitals and the carbon's 2s.

Since this MO is both bonding and occupied it'll have a large effect on the bonding in methane.

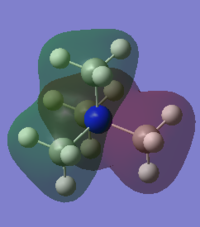
MOs 3, 4 & 5

These MOs are all degenerate with an energy of -0.38831 Hartrees.

They are bonding orbitals from the hybridization of the 2p orbitals in the carbon and the 1s of the hydrogens.

Since these MOs are both bonding and occupied they'll have a large effect on the bonding in methane.

This is methanes HOMO.

MO 6

This has a high energy of 0.11824 Hartrees.

It is the anti bonding orbital formed from the hybridization of the 2s on carbon and 1s of the hydrogens.

This orbital is unoccupied and so it doesn't have an effect on the bonding in methane.

It is the LUMO.

MOs 7, 8 & 9

These MOs are degenerate and high in energy, 0.17677 Hartrees.

They are anti bonding orbitals formed from the hybridization of the 2p orbitals on the carbon and the 1s of the hydrogens.

These orbitals are unocuppied and so they don't have an effect on the bonding in methane.