Rep:Mod:01190874

Annie Rouse, CID=01190874

NH₃

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

The energy was calculated to be: -56.55776873 (au)

RMS Gradient: 0.00000485

Point Group: C_3V

Bond distance: 1.01798 angstrom

Bond angle: 105.741 degrees

The table showing that the calculations converged is below:

Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

My .log file is here

Ammonia

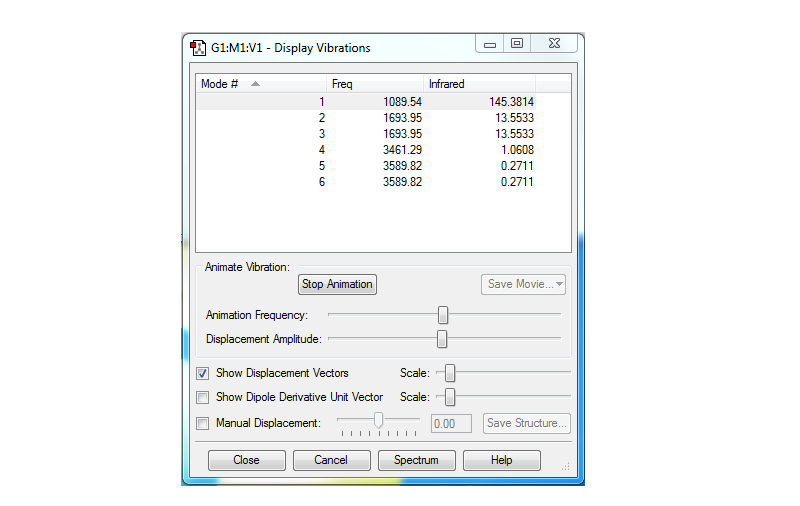
Below is a screenshot showing the vibrational modes calculated for the molecule.

From the 3N-6 rule, 6 modes are expected and 6 are observed, since N is 3.

There are 2 pairs of degenerate modes (2 and 3, 5 and 6).

1,2 and 3 are bending and 4, 5 and 6 are stretching.

The 4th mode is highly symmetric (ie. the symmetric stretch mode) whereas modes 5 and 6 are asymmetric stretches.

Umbrella mode is the 1st mode (when the molecule opens and closes like an umbrella - this is a bending mode)

2 bands expected in experimental IR, since there are 2 distinct energies at which a change in dipole moment would be induced - one of the pairs of degenerate modes is not IR active as it does not induce a change in dipole moment (modes 5 and 6), the first pair of degenerate modes only produces one band since, and the 4th mode (highly symmetric) does not induce a change in dipole moment and thus would not produce a band in the IR spectrum.

The charges on the atom were calculated as follows: H has charge 0.375; N has charge -1.125. This is in accordance with expected results since N is more electronegative than H and thus would be expected to bear more negative charge in a compound with only H.

N₂

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

The final energy was calculated to be: -109.52412868 (au)

RMS Gradient Norm: 0.00000060

Point group: D_infh

Bond length: 1.10550 angstrom Bond angle: 180 degrees

The table showing the calculations converged is below:

 Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

There is only one vibrational mode, a stretching mode at 2457.33 cm^-1.

This is in accordance with the 3N -5 rule (since N is 2). The 3N -5 rule is used since this molecule is linear.

The charges on each atom are 0 since this is a homonuclear diatomic and there is no difference in electronegativity.

My .log file is here

H₂

Calculation Method: RB3LYP

Basis Set: 6-31G(D,P)

E(RB3LYP): -1.17853936 (au)

RMS Gradient Norm: 0.00000017

Point group: D_infh

Bond length: 0.74279 angstrom

Bond angle: 180 degrees

The table showing that the calculations converged is below:

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

There is only one vibrational mode, a stretching mode at 4465.68 cm^-1

This is in accordance with the 3N -5 rule (this rule is used since the molecule is linear), and since N is 2.

The charges on the atoms are 0 since this is a homonuclear diatomic and there is no difference in electronegativity.

My .log file is here

Reaction Energy Calculations

In order to find the reaction enthalpy for the Haber-Bosch process: N₂ + 3H₂ -> 2NH₃

E(NH3)= -56.55776873

2*E(NH3)= -113.115537

E(N2)= -109.52412868

E(H2)= -1.17853936

3*E(H2)= -3.53561808

ΔE=2*E(NH₃)-[E(N₂)+3*E(H₂)]= -0.05579024 (au)

Thus the reaction enthalpy of the Haber-Bosch process is -146.48 kJmol^-1 (the result in au above was multiplied by 2625.5 to convert it into kJmol^-1).

Thus the product (N₃) is more stable than the reactants (N₂ and H₂), as the energy change is negative and the product is lower in energy than the reactants.

A literature value for the enthalpy of the formation of ammonia (essentially what has been calculated above) is −46.22 kJ/mol The difference between the enthalpy calculated here and the literature value could be attributed to several different factors, particularly that the optimised energies for the molecule are theoretical only and depend on the calculation method use, and therefore may not represent accurately what is physically observed in reality.

H₂O

H₂O

Point group: C_2V

Calculation Method: RB3LYP

Basis Set: 6-31G(d,p)

The final energy was calculated to be: -76.41973740 (au)

RMS Gradient Norm: 0.00006276

Bond length: 0.96522 angstrom

Bond angle: 103.745 degrees

The table showing the calculations converged is below:

Item               Value     Threshold  Converged?
 Maximum Force            0.000099     0.000450     YES
 RMS     Force            0.000081     0.000300     YES
 Maximum Displacement     0.000128     0.001800     YES
 RMS     Displacement     0.000120     0.001200     YES

My .log file is here

Water

The charge on the H atoms is: 0.472

Charge on the O atom: -0.944

The charges make sense, since O is more electronegative than H.

There are 3 vibrational modes, which is in accordance with the 3N-6 rule (used since this molecule is non linear, and N is 3).

The first, at 1665.00 cm^-1 is a symmetrical bending mode.

The second, at 3801.05 cm^-1 is a symmetrical stretch.

The third, at 3914.23 cm^-1 is an asymmetric stretch.

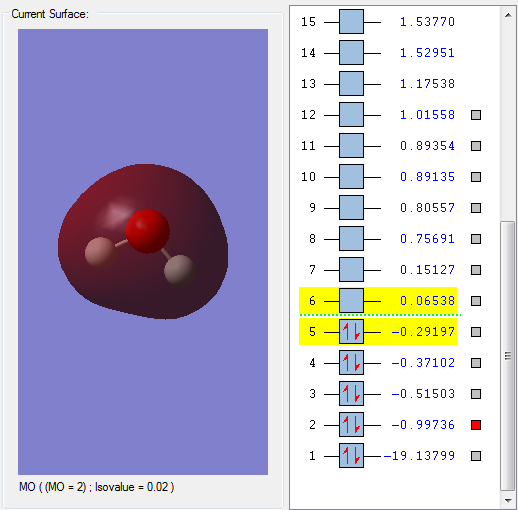
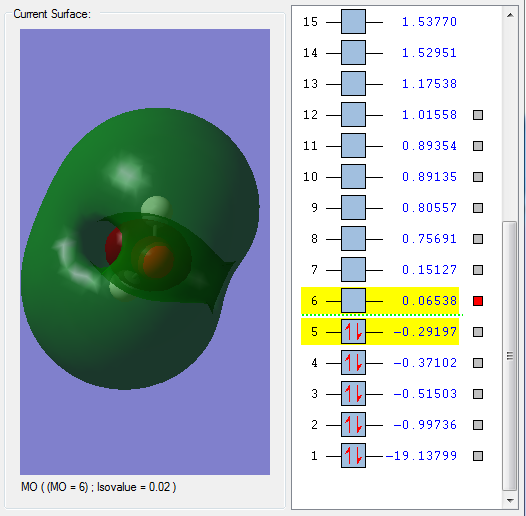
This is a sigma orbital formed by overlap of the 1s orbitals on the H atoms, and the 2s orbital on an O atom. It is deep in energy (the deepest energy bonding orbital) and is fully occupied. There are no nodes across bonds and thus this is a bonding orbital.

This is a sigma orbital formed by overlap of a 2p orbital on the O atom and the 1s orbitals on the H atoms. It is fully occupied, and is an bonding orbital, as the node is across the O atom not the O-H bonds. It is evident that this MO is formed by overlap of a 2p orbital and a 1s orbital because the node across the O atom indicates a p orbital is involved. It is quite deep in energy.

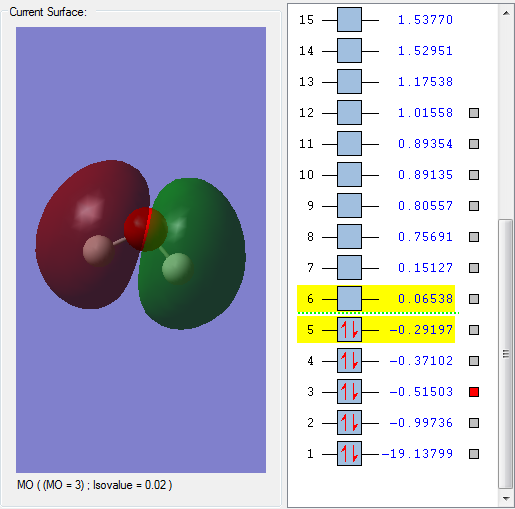
This orbital is a non-bonding orbital accounting for the lone pair characteristics of the O on water. It is fully occupied, and is the last MO to be fully occupied - this is the HOMO. There is negligible contribution from the 1s orbitals on the H atoms, so this orbital has mostly p character.

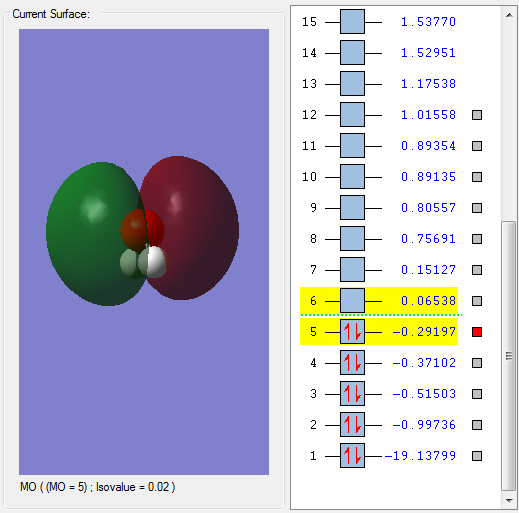
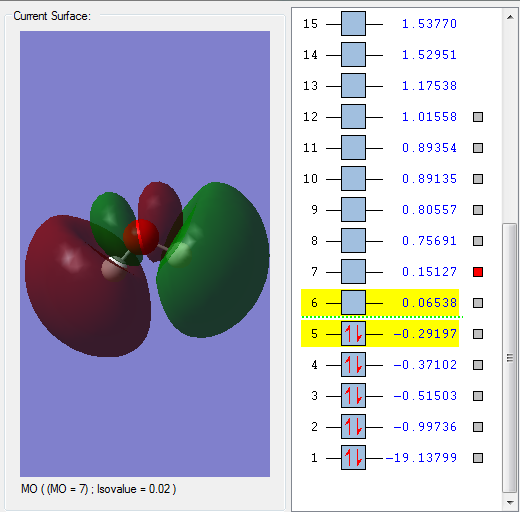
This orbital is formed by overlap of a 2p orbital on the O atom and the 1s orbitals on the H atoms. It is the first unoccupied MO and thus this is the LUMO, and is an antibonding orbital as there are nodes across the O-H bonds. It contributes to the reactivity of water, as if another species attacks a water molecule, it interacts with this MO.

This orbital is formed by overlap of a 2p orbital on the O atom and the 1s orbitals on the H atoms. It is an antibonding orbital, as there are nodes across the O-H bonds, and is relatively high in energy (positive) and thus doesn't contribute a great deal to the bonding in H₂O.